高超声速飞行器的多幂次滑模控制①
方 雪,杨文骏,樊 征,张 科
(1.西北工业大学 招标与设备采购中心,西安 710072;2.航天飞行动力学技术重点实验室,西安 710072; 3.西北工业大学 航天学院,西安 710072)
0 引言
高超声速飞行器(Hypersonic Flight Vehicle, HFV)有速度高、机动性强、具备全球打击能力等诸多优点,在军事和民用方面都具有巨大的应用价值。近年来,许多国家和科研机构都大力开展高超声速相关技术的研究,掀起了高超声速飞行器的研究热潮[1-3]。但也因其具有强非线性、强耦合性和快时变等特点,对其进行控制器设计就更困难,也更具挑战性[4-6]。
文献[7-13]分别采用增益调度、鲁棒控制、反演控制和滑模控制等控制方法实现了高超声速飞行器的飞行控制系统设计。滑模控制对扰动和不确定性具备良好的鲁棒性,得到了广泛关注和应用,但传统滑模存在抖振和收敛速度慢等问题,限制了其发展及应用。而通过提高趋近律阶次改善滑模控制的品质,是一种简便有效的方法。文献[14]提出了一种采用双幂次趋近律提高系统状态收敛速度的设计方案,使得在不确定性影响下,系统状态及导数可快速收敛到平衡点的邻域。文献[15]设计了一种基于特定双幂次趋近律的滑模控制方法,并分析了其全局快速收敛特性。文献[16]提出了一种基于新型双幂次组合函数的滑模控制方案,保证系统全局固定时间收敛的同时,具有更快的收敛速度。文献[17]则提出了一种多幂次滑模趋近律,通过三个幂次项系数在系统趋近过程的不同阶段进行针对性调节,显著提高了系统的收敛速度。
针对系统同时存在参数不确定项和外部扰动的影响,采用干扰观测器对其进行估计补偿是一种有效可行的方法。扩张状态观测器[18](Extended State Observer,ESO)模型依赖性低,设计简便,能实现对系统不确定性和外部扰动等的有效估计。文献[19]设计了含ESO的非线性动态逆控制器,实现了高超声速飞行器在模型不确定和外部扰动影响下对速度和高度的稳定跟踪。Gao[20]在此基础上,提出了设计更简便的线性扩张状态观测器(Linear Extended State Observer,LESO)。文献[10]采用LESO实现了对高超声速飞行器巡航飞行过程中存在的模型不确定性和外界干扰精确估计,结合所设计的动态面控制器,保证了速度和高度的高精度指令跟踪性能。
本文针对存在模型参数不确定项和外部扰动的高超声速飞行器纵向模型,设计了基于多幂次趋近律的滑模控制器,并采用LESO对模型参数不确定项和外部扰动组成的集总扰动进行估计补偿,最后理论证明了所设计控制器能保证系统的闭环稳定性,并通过仿真实例验证了其有效性。
1 高超声速飞行器模型
本文采用文献[10,19]中的HFV纵向模型,利用非线性动态逆技术,经精确反馈线性化后,系统可描述为
(1)
式中V和H分别为HFV的速度和高度;βc和δe分别为发动机节流阀开度和升降舵偏转;FV、FH和B的详细表达式可参考文献[10,19,21]。
假设1 控制矩阵B非奇异。
注1 考虑到HFV在巡航飞行过程中,航迹角很小,HFV的飞行航迹不可能是垂直的,故矩阵B非奇异。
考虑HFV的模型参数不确定性:
(2)
式中 “●0”为参数标称值;“Δ●”为参数偏移量。
参数偏移量满足约束条件:
(3)
引入外部扰动,则系统动态可表述为
(4)
式中 ΔFV、ΔFH和ΔB为系统不确定项;B0为标称控制矩阵;d1(t)和d2(t)为外部扰动。
系统对ΔB的敏感程度要远高于ΔFV和ΔFH,故ΔFV和ΔFH可忽略不计[21]。故式(4)可改为
(5)
其中,dv(t)和dh(t)为速度和高度通道中的系统不确定项和外部扰动组成的集总扰动,如式(6):
(6)
2 控制系统设计
2.1 多幂次滑模控制器设计
暂不考虑系统的集总扰动,针对速度和高度子系统,定义滑模面:
(7)
式中ev=V-Vd;eh=H-Hd;Vd和Hd分别为速度和高度指令;p1和p2为所需设计的正数。
式(7)求导可得
(8)
其中
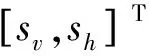
设计多幂次滑模控制器(Multi Power Sliding Mode Controller, MPSMC)为
(9)
其中
ψ1=-kv,1sigc1(sv)-kv,2sigc2(sv)-kv,3sigc3(sv)-kv,4sv
ψ2=-kh,1sigc1(sh)-kh,2sigc2(sh)-kh,3sigc3(sh)-kh,4sh
其中,sigc(s)=|s|csgn(s);kv,j,kh,j>0(j=1,2,3,4);
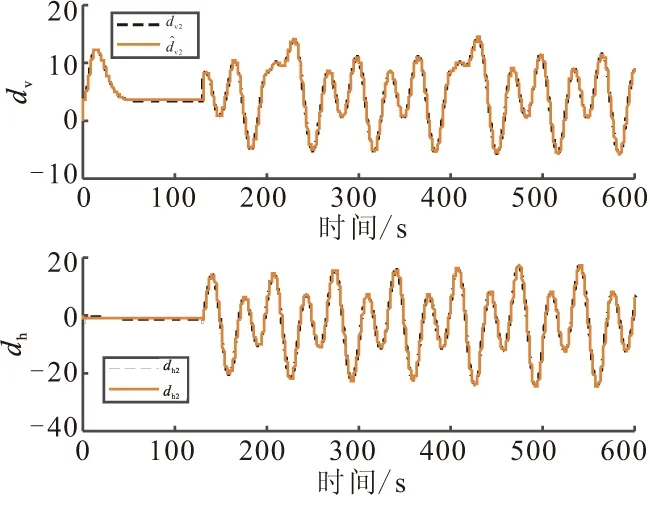
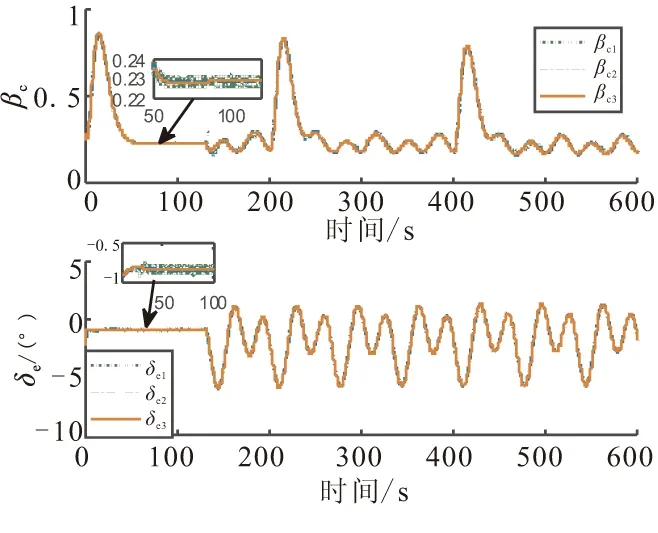
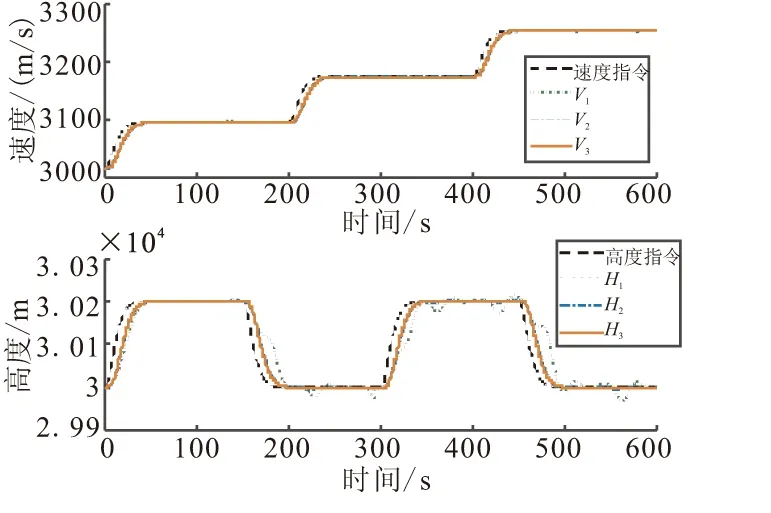
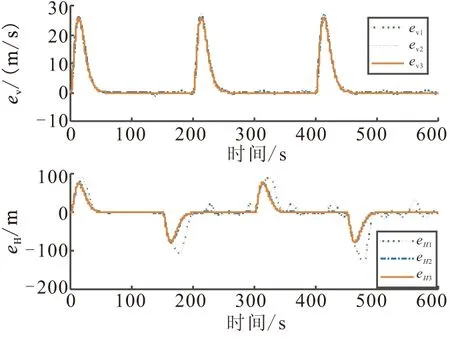
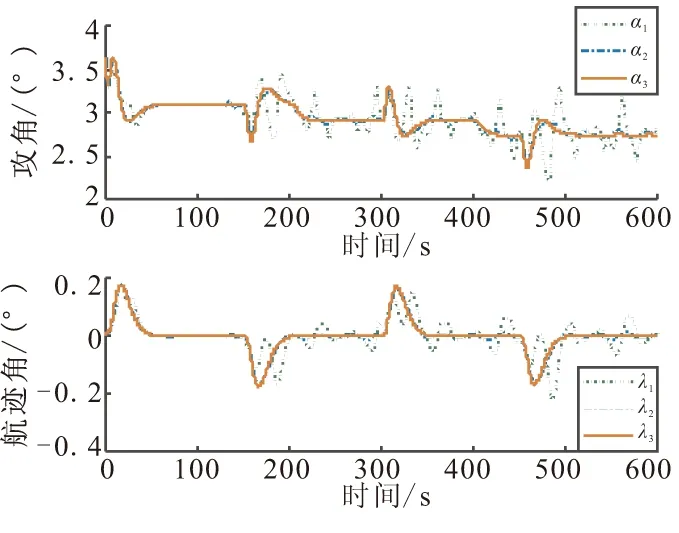
c1>0,0 (10) 将控制器(9)代入式(8)中,可得 (11) 当系统状态满足|si|<1时,式(11)主要受-ki,2sigc2(si)-ki,3sigc3(si)的影响;系统状态满足|si|≥1时,式(11)主要受-ki,1sigc1(si)-ki,3sigc3(si)的影响。c3的取值可保证系统在状态满足|si|>c1或|si| (12) 对式(12)沿式(8)求导可得 (13) 故两个子系统的滑模面均满足可达性条件,sv和sh将在有限时间内渐近收敛到零。根据滑模面定义式(7),速度和高度的指令跟踪误差也将渐近收敛到零,故系统是渐近稳定的。 (14) 针对系统(14)设计二阶LESO: (15) (16) λ0(s)=s2+l1s+l2=(s+ω0)2 (17) 只要满足ω0>0,式(17)就具有负实部根,保证了A是Hurwitz稳定的。令ω0=1/ε,则有li=αi/εi,取gi(e1(t))=αie1(t),式(15)可转换为 (18) 定义: (19) 则系统(18)对系统(14)的观测误差动态为 (20) 假设2[10]HFV速度和高度通道的集总扰动dv(t)和dh(t)属于C1类函数且其一阶导数有界。 注2 HFV巡航飞行过程中,其参数不确定性和外部扰动均在一定范围内。 假设3[10]∀ζ(t)=[ζ1(t),ζ2(t)]T∈R2,存在常数λi(i=1,2,3,4),β以及连续可微、径向无界的正定函数V,W:R2→R,满足如下条件: (i)λ1‖ζ‖2≤V(ζ)≤λ2‖ζ‖2,λ3‖ζ‖2≤W(ζ)≤λ4‖ζ‖2; ∀t∈[tε,∞) (21) 参数ε取得足够小即LESO的带宽ω0取得足够大时,所设计的LESO能有效估计系统(14)的状态,其估计误差收敛于O(ε3-i)。ω0的取值越大,LESO的响应速度越快,估计精度越高,但(由于高增益)容易引起明显的峰值现象,同时也会减弱其对高频噪声的抑制能力,继而影响系统的稳定性和跟踪精度,因此ω0的选取应在保证LESO的响应速度和估计精度与满足系统性能要求之间取折中。 保持参数设置不变,将该LESO应用于速度子系统即可实现对速度通道集总扰动的估计补偿。最终可得含LESO估计补偿的多幂次滑模控制器: (22) 将式(5)代入系统(8)中,可得 (23) 式中d=[dv(t),dh(t)]T。 定理2 考虑系统不确定项和外部扰动,针对系统(5),设计控制器如式(22),能保证系统是渐近稳定的,且系统滑模面能在有限时间内收敛到区域: (24) 证明 选取Lyapunov函数如式(12),对其沿式(23)求导可得 (25) 代入控制器(22),可得 (26) (27) 取k4=min(kv,4,kh,4),式(27)可变换为 (28) (29) 由引理1可知,系统滑模面s可在有限时间内收敛到原点的邻域(24)内,通过合理的参数设置可使该邻域任意小,故系统是渐近稳定的,根据2.1节,速度和高度的跟踪误差也渐近收敛到零。因此,所设计控制器(22)能够保证系统在参数不确定性和外部扰动的综合影响下的渐近稳定性。 证毕。 以高超声速飞行器巡航飞行为例,对本文所提出的LESO和多幂次滑模控制器进行仿真验证。飞行器初始参数为:速度V=3016.152 m/s,高度H=30 km,攻角α=3.625°,航迹角γ=0°,节流阀开度βc=0.258,升降舵偏角δe=0.656°。速度通道每200 s给予80 m/s的阶跃指令信号,高度通道参考指令是幅值为200 m的方波信号,参考指令均通过二阶参考模型后给出。从仿真的130 s开始引入外部扰动 (30) 为验证所设计控制器的有效性,在相同的仿真条件下,与传统滑模控制器(Conventional Sliding Mode Controller, CSMC)及双幂次滑模控制器[14-15](Double Power Sliding Mode Controller,DPSMC)进行对比,其双幂次趋近律如 (31) 滑模面参数取为:p1=0.3,p2=0.38;控制器参数选取为:a1=0.7,a2=0.9,b1=1.5,b2=0.5;ki,1=0.7,ki,2=0.9,ki,3=1.2,ki,4=1.5,c1=1.5,c2=0.5,i=v,h;LESO的带宽取为:ω0=10。 仿真结果如图1~图6所示。图中下标“1”表示CSMC+LESO,下标“2”表示DPSMC+LESO,下标“3”表示MPSMC+LESO。图1和图2分别表示了高超声速飞行器的速度和高度跟踪曲线及其跟踪误差曲线,图3为攻角和航迹角响应曲线,图4为速度和高度子系统滑模面,表1给出平均绝对误差(Mean Absolute Error,MAE)、平均相对误差(Mean Relative Error,MRE)、均方误差(Mean Squared Error,MSE)和均方根误差(Root Mean Square Error,RMSE)评价指标(均是评估值越小,表明跟踪精度越高)框架下的速度和高度指令跟踪误差评估数据。 图1 速度和高度指令跟踪Fig.1 Velocity and altitude command tracking 图2 速度和高度指令跟踪误差Fig.2 Velocity and altitude commandtracking errors 图3 攻角和航迹角响应曲线Fig.3 Responses of angle of attack andflight-path angle 图4 速度和高度子系统滑模面Fig.4 Sliding surfaces of velocity andaltitude subsystem 由图1~图3可知,在本文所设计的控制方案作用下,速度和高度跟踪误差均能快速收敛到零,攻角和航迹角也能较快趋于平衡状态,且在整个飞行过程中都处在合理范围内,和其他两种控制方案相比,尤其在引入外部扰动之后,本文控制器展现了更好的扰动抑制能力,稳态性能更优。从图4中可看出,本文控制器使得系统在远离滑模面和接近滑模面时均具备更快的收敛速度,且当存在外部时变扰动时,系统能保持稳定在平衡点附近小邻域内,无抖振现象,而传统滑模控制器和双幂次滑模控制器则均存在较大波动。表1中的数据也表明本文控制器的性能更优。 表1 速度和高度指令跟踪误差评估 图5为本文控制器作用下的集总扰动估计曲线,可以看出,所设计的LESO能对集总扰动进行有效估计,实现在控制器中的动态补偿,从而增强控制器的扰动抑制能力。图6为控制输入曲线,传统滑模控制器的控制量全程伴有轻微的抖振现象,双幂次及多幂次控制方案的控制量都维持在合理范围内且较平滑,不存在抖振现象,130 s后开始的波动抑制了外部扰动的影响,保证了飞行的稳定性。 (1)设计基于多幂次趋近律的滑模控制器,和基于双幂次趋近律的滑模控制器相比,使得系统具有更好的指令跟踪性能和抗干扰能力,且在远离和接近滑模面时收敛速度更快。 (2)利用系统精确反馈线性化的部分信息,设计二阶线性扩张状态观测器(LESO)对系统不确定项和外部扰动进行估计,估计值用于控制系统的动态补偿,显著提升了控制器的扰动抑制能力和系统的鲁棒性。 图5 集总扰动估计Fig.5 Estimation of lumped disturbances 图6 控制输入Fig.6 Control inputs 参考文献: [1] 方洋旺,柴栋,毛东辉,等.吸气式高超声速飞行器制导与控制研究现状及发展趋势[J].航空学报,2014,35(7):1776-1786. FANG Yangwang,CHAI Dong,MAO Donghui,et al.Status and development trend of the guidance and control for air-breathing hypersonic vehicle[J].Acta Aeronautica et Astronautica Sinica,2014,35(7):1776-1786. [2] 翟岱亮,雷虎民,李海宁,等.面向轨迹预测的高超声速飞行器气动性能分析[J].固体火箭技术,2017,40(1):115-120. ZHAI Dailiang,LEI Humin,LI Haining,et al.Trajectory prediction oriented aerodynamic performances analysis of hypersonic vehicles[J].Journal of Solid Rocket Technology,2017,40(1):115-120. [3] Parker J T,Serrani A,Yurkovich S,et al.Control-Oriented Modeling of an Air-Breathing Hypersonic Vehicle[J].Journal of Guidance,Control,and Dynamics,2007,30(3):856-869. [4] 孙长银,穆朝絮,余瑶.近空间高超声速飞行器控制的几个科学问题研究[J].自动化学报,2013,39(11):1901-1913. SUN Changyin,MU Chaoxu,YU Yao.Some control problems for near space hypersonic vehicles[J].Acta Automatica Sinica,2013,39(11):1901-1913. [5] 王易南,陈康,符文星,等.带有攻角约束的高超声速飞行器航迹倾角跟踪控制方法[J].固体火箭技术,2016,39(1):125-130. WANG Yinan,CHEN Kang,FU Wenxing,et al.Hypersonic flight vehicle's flight path angle tracking control with attack angle constraints[J].Journal of Solid Rocket Technology,2016,39(1):125-130. [6] Guo Z Y,Zhou J,Guo J G,et al.Coupling-characterization-based robust attitude control scheme for hypersonic vehicles[J].IEEE Transactions on Industrial Electronics,2017,64(8):6350-6361. [7] 孙辰昕.高超声速飞行器的增益调度控制器设计[D].哈尔滨:哈尔滨工业大学,2016. SUN Chenxin.The design of gain scheduling controller of hypersonic vehicle[D].Harbin:Harbin Institute of Technology,2016. [8] 李昭莹,余令艺,刘昊,等.高超声速飞行器非线性鲁棒控制律设计[J].控制理论与应用,2016,33(1):62-69. LI Zhaoying,YU Lingyi,LIU Hao,et al.Nonlinear robust controller design for hypersonic vehicles[J].Control Theory & Applications,2016,33(1):62-69. [9] 卜祥伟,吴晓燕,白瑞阳,等.基于滑模微分器的吸气式高超声速飞行器鲁棒反演控制[J].固体火箭技术,2015,38(1):12-17. BU Xiangwei,WU Xiaoyan,BAI Ruiyang,et al.Sliding-mode-differentiator-based robust backstepping control of air-breathing hypersonic vehicles[J].Journal of Solid Rocket Technology,2015,38(1):12-17. [10] 杨文骏,张科,王佩.含LESO的高超声速飞行器动态面控制[J].宇航学报,2017,38(8):830-838. YANG Wenjun,ZHANG Ke,WANG Pei.LESO-based dynamic surface control for a hypersonic flight vehicle[J].Journal of Astronautics,2017,38(8):830-838. [11] 耿洁,刘向东,王亮.高超声速飞行器的动态滑模飞行控制器设计[J].兵工学报,2012,33(3):307-312. GENG Jie,LIU Xiangdong,WANG Liang.Dynamic sliding mode control of a hypersonic flight vehicle[J].Acta Armamentarii, 2012,33(3):307-312. [12] Zong Q,Wang J,Tian B L,et al.Quasi-continuous high-order sliding mode controller and observer design for flexible hypersonic vehicle[J].Aerospace Science and Technology,2013,27(1):127-137. [13] Zhang R M,Sun C Y,Zhang J M,et al.Second-order terminal sliding mode control for hypersonic vehicle in cruising flight with sliding mode disturbance observer[J].Journal of Control Theory and Applications,2013,11(2):299-305. [14] 张合新,范金锁,孟飞,等.一种新型滑模控制双幂次趋近律[J].控制与决策,2013,28(2):289-293. ZHANG Hexin,FAN Jinsuo,MENG Fei,et al.A new double power reaching law for sliding mode control[J].Control and Decision,2013,28(2):289-293. [15] 李慧洁,蔡远利.基于双幂次趋近律的滑模控制方法[J].控制与决策,2016,31(3):498-502. LI Huijie,CAI Yuanli.Sliding mode control with double power reaching law[J].Control and Decision,2016,31(3):498-502. [16] 廖瑛,杨雅君,王勇.滑模控制的新型双幂次组合函数趋近律[J].国防科技大学学报,2017,39(3):105-110. LIAO Ying,YANG Yajun,WANG Yong.Novel double power combination function reaching law for sliding mode control[J].Journal of National University of Defense Technology,2017,39(3):105-110. [17] 张瑶,马广富,郭延宁,等.一种多幂次滑模趋近律设计与分析[J].自动化学报,2016,42(3):466-472. ZHANG Yao,MA Guangfu,GUO Yanning,et al.A multi power reaching law of sliding mode control design and analysis[J].Acta Automatica Sinica,2016,42(3):466-472. [18] 韩京清.自抗扰控制技术--估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2008. HAN Jingqing.Active disturbance rejection control technique-the technique for estimating and compensating the uncertainties[M].Beijing:National Defense Industry Press,2008. [19] 杨文骏,张科,张明环,等.基于ESO的高超声速飞行器非线性动态逆控制[J].西北工业大学学报,2016,34(5):805-811. YANG Wenjun,ZHANG Ke,ZHANG Minghuan,et al.ESO based nonlinear dynamic inversion control for hypersonic flight vehicle[J].Journal of Northwestern Polytechnical University,2016,34(5):805-811. [20] Gao Z Q.Active disturbance rejection control:a paradigm shift in feedback control system design[C]// Proceedings of the 2006 American Control Conference,Minneapolis,USA,June 14-16,2006:2399-2405. [21] Xu H J,Mirmirani M D,Ioannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle[J].Journal of Guidance,Control,and Dynamics,2004,27(5):829-838. [22] Bhat S P,Bernstein D S.Finite-time stability of continuous autonomous systems[J].SIAM Journal of Control and Optimization,2000,38(3):751-766. [23] Aghababa M P,Khanmohammadi S,Alizadeh G.Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique[J].Applied Mathematical Modelling,2011,35(6):3080-3091.2.2 LESO设计
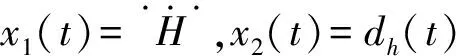


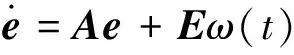




2.3 稳定性分析
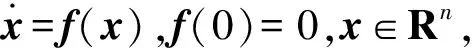

3 仿真验证


4 结论