临近空间拦截弹中制导弹道设计①

李宁波，邵 雷，王华吉，雷虎民，龙振国

(1.空军工程大学 防空反导学院，西安 710051；2.中国人民解放军95100部队，广州 510405)

0 引言

近年来，临近空间高超声速武器迅猛发展使其成为国家安全的现实威胁[1-2]，研究反临近空间的先进拦截技术和防御手段已迫在眉睫。从目前的研究现状来看，国外关于反临的研究文献很少，其主要以进攻型高超声速飞行器为背景，但也可以为反临研究提供借鉴。国内方面，许多学者开展了积极的探索，提出了有益的思路，对临近空间高超声速目标拦截难点的认识逐渐统一，并逐步形成空基拦截和地基拦截两类主流思想[3-4]。但对于拦截弹的弹道设计目前还没有定论，有待研究和完善。

面对临近空间高超声速武器这类新型、高动态目标，拦截弹应采用复合制导体制，远程、梯次进行拦截，从而保证拦截的成功率。由于拦截弹大部分时间飞行在中制导段，因此中制导段的飞行性能决定了整体性能。传统防空导弹制导律研究主要基于弹目的运动关系设计导引律，弹道由导引律决定。考虑到临近空间拦截问题中各种严格的限制条件，在中制导律的设计过程中必须要考虑到弹道的优化设计，以提高拦截效率。

弹道设计问题一直是飞行器研究领域的热点。文献[5-6]分别研究了初始及终点位置固定、飞行时间受约束和考虑地球偏率影响的大气层外弹道规划问题。文献[7]提出了使相对位置向量与速度向量共线的中制导飞行策略，研究了大气层外中制导段的弹道。文献[8]对防空导弹中制导段弹道优化问题进行了较为全面的论述，同时也给出了准最佳弹道的相关理论和实现方法。文献[9]研究了虚拟域动态逆的方法，并将其应用于空地反辐射导弹的弹道优化设计。

虽然许多学者对弹道优化设计问题进行了深入的探索，但是对于以反临拦截弹为背景的研究却很少。本文以地基拦截临近空间高超声速目标为背景，根据临近空间目标特点及拦截作战要求，设计了一种高抛再入的弹道方案，并分析了中末制导交接班问题从而为建立中制导终端约束模型的建立提供参考。

1 弹道方案设计

1.1 目标弹道特性分析

目前，典型的高超声速助推滑翔飞行器主要以HTV-2和AHW为代表，本文以HTV-2为拦截目标进行弹道特性分析。

Lu Ping等[10]研究了HTV-2的两种弹道模式，一种是采用弹道式发射，助推段完成后的终端状态与弹道导弹类似，试验飞行器先飞出大气层，之后再入至临近空间高度进行平衡滑翔飞行；另一种在助推级利用发动机推力直接将飞行轨迹调整为平衡滑翔模式。两种模式的飞行弹道相比于弹道导弹，其飞行高度都大大的降低，与弹道导弹长时间在大气层外飞行不同，HTV-2将长时间在大气层内的临近空间高度飞行，且其通常采用空气动力控制[11]。不管采用何种模式，HTV-2都将长时间在30～60 km高度的范围内滑翔飞行，且其飞行弹道较为平稳。此外，通过分析速度剖面可发现，两者的速度最高都可达到6000～7000 m/s，而在滑翔段的末端其速度一般只有2000 m/s左右。因此，从速度的角度看，滑翔段的末端部分是一个适合拦截的窗口。

另一方面，在滑翔段目标航迹较为平稳，易于探测发现并进行稳定跟踪，拦截窗口较大，将该段作为目标与拦截弹的交会时间段，有利于对目标轨迹预测计算，目标可用过载较小。在一定程度上可降低对拦截弹的过载要求。另外，从拦截弹的控制角度考虑，临近空间下层高度范围内存在有稀薄大气，有利于对拦截弹实施气动控制，减少直接力控制的使用。

1.2 弹道与导引律分离设计

在制导律设计中，防空导弹通常都以最速接近为目标。通过数学方法可证明，前置法、半前置法、三点法等遥控指令制导方法，和追踪法、平行接近法、比例导引法等寻的制导方法，其本质上都是根据不同初始条件，以最速接近为性能指标推导得到的。由于临近空间拦截弹的作战距离相对较远，如果采用上述的基于弹目相对运动关系的拦截导引策略，将会导致拦截武器制导指令的频繁调整，造成更多能量损耗。

对高超声速目标拦截问题，当采用弹道与导引律分离设计策略时，中制导段拦截弹弹道无需随目标运动进行实时调整，只有当终端约束条件发生大的变化时才需相应的弹道调整，以保证拦截弹以较好的相对阵位进入末制导，因此中制导段合理设计优化弹道有利于提高飞行品质，从而达到有效命中目标的目的[12]。

另一方面，拦截弹飞行过程中，其结构强度、热防护、发动机正常工作以及控制稳定性等一系列问题对热流密度、动压、过载、控制量等过程特征提出了严格的要求，上述导引律难以将各种约束考虑其中。综上，为了克服以上的缺点，提升拦截弹的性能，应将弹道和导引方法分离设计。

1.3 高抛再入弹道

由于地基拦截弹从地面发射，如果按照传统弹道设计，将会导致拦截弹的飞行弹道全程处于目标的下方，由于下方的空气阻力相对较大，因此与目标相比，拦截弹处于不利地位，也限制了拦截弹的射程。如果按照抛物线弹道飞行，先向上进行爬升，然后再沿抛物线下降，末制导段的弹道按照寻的导引律飞行，此时大部位的弹道将会处于目标上方，空气阻力降低，拦截弹射程也将会大大增加。

此外，由于临近空间及其上部空域大气相对稀薄，其空气中的红外吸收物质较少，所以导引头的探测视角应采用自上而下的方式[13]。另一方面，拦截弹长期在目标上方的稀薄大气中飞行，可降低导引头和弹体的气动加热，为导引头提供较好的初始工作条件。综上，本文提出拦截弹采用高抛再入的拦截弹道方案，此处“再入”不是指传统意义上的从大气层外再入，而是指拦截弹向上爬升后在下降飞行的过程。

根据上述设计思想，拦截弹的弹道将按照不同的飞行过程划分为如下四个阶段：

(1)无控段：假设拦截弹采用垂直发射模式，冷弹升起以后，在空中进行点火，垂直飞行一定高度后，制导雷达捕获拦截弹，这段时间仅进行拦截弹的稳定控制。

(2)转弯段：从启控点开始，到助推发动机熄火关机，与弹体分离，本章的设计为两级的火箭助推发动机。该阶段拦截弹的速度和弹道倾角的变化范围较大。

(3)滑翔段：从助推发动机关机分离开始，到导引头捕获目标，顺利实现中末制导交接班为止。该阶段拦截弹进行无动力滑行，不断接近目标，飞行状态较为平稳。

(4)末制导段：从顺利实现中末制导交接班开始，到精确命中目标为止。该阶段拦截弹在寻的导引律的作用下，直接飞向目标，进行碰撞杀伤。

上述过程中，无控段垂直上升，没有必要对弹道进行优化。本文所研究的中制导段为转弯段和滑翔段。图1为拦截过程的弹道示意图。

图1 拦截弹全程弹道示意图Fig.1 Schematic diagram of the whole trajectory

2 拦截弹弹道优化模型

2.1 拦截弹运动方程

中制导段拦截弹应朝向终端位置约束飞行，理想轨迹位于拦截弹与目标所在的纵向平面内。另一方面，在实际飞行的过程中，由拦截弹偏离预定弹道平面造成的侧向运动参数的变化量相比于纵向参数的变化都是小量，其实际飞行弹道与纵向平面内的弹道差别不大，所以可将纵向运动和侧向运动分开来研究[14]。因此，考虑如下纵向平面内的拦截弹质点运动模型：

(1)

(2)

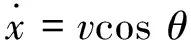
(3)

(4)

式中v为拦截弹速度；θ为弹道倾角；x、y分别为拦截弹在大地惯性坐标系下的位置；m为拦截弹质量；q为动压；S为参考面积；g为重力加速度；P为作用在拦截弹上的推力。

为了使拦截弹达到较高的飞行速度，需要大推力助推加速，初步设计了两级助推方案，推力计算公式如式(5)所示[15]：

(5)

式中Ve为燃气速度；Isp为比冲，对固体火箭发动机，其值一般为200～300 s。

发动机的相关参数设计如表1所示。

表1 拦截弹助推发动机相关参数

阻力系数及升力系数Cx、Cy可以分别表示为马赫数Ma和攻角α的函数：

(6)

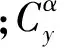
对大气密度的假设：

ρ=ρ0exp(-y/y0)

(7)

式中ρ0为地面空气密度，ρ0=1.225 0 kg/m3；ρ为飞行器高度处的空气密度；y0=7254.3 m。

2.2 目标函数与过程约束

设t0表示初始时刻，tf表示终端时刻，为保证拦截弹的杀伤效果，一般将终端时刻的速度最大作为优化指标J，即：

J=minφ(v(tf)，tf)=min{-vf}

(8)

为保证飞行的稳定性，对拦截弹攻角大小应加以限制。控制量约束设置如下：

‖α‖≤αmax

(9)

动压极限值主要取决于热防护材料强度与气动控制铰链力矩。其约束设置为

q=0.5ρv2≤qmax

(10)

在临近空间范围内，拦截弹所能提供的可用过载大小有限，过载约束设置为

(11)

考虑到拦截弹的热流密度约束，其简化计算公式为[16]

(12)

3 反临拦截弹中末制导交接班分析

高精度的复合制导技术是拦截临近空间高超声速目标的关键技术之一，复合制导包含了初、中、末制导以及各段间的交接班。其中，实现中末制导交接班较为困难，成为防御此类目标的瓶颈问题。

对于低速目标来说，交接班约束较为宽松，末制导的捕获状态空间较大，且拦截常规目标时对脱靶量要求并不严苛，可认为中末交接班瞬间完成。对高超声速目标来说，随着目标速度增大，末制导捕获状态空间会急剧减小，拦截弹要想以很小的脱靶量击中目标，就必须快速满足中末制导交接班的各类复杂约束，主要包括导引头截获条件约束和末制导捕获条件约束。导引头截获[17]包括距离截获、角度截获和速度截获，保证拦截弹能“看得到目标”，此约束条件形式简单，容易描述。末制导捕获条件约束主要由弹目相对距离矢量、拦截弹及目标速度矢量组成，保证拦截弹能“打得上目标”，对此约束的描述较为困难。本节侧重研究末制导捕获条件以及它对中末交接班的影响，最终目的是为中制导设计弹道终端约束条件提供参考。

3.1 弹目相对运动模型

中制导的终端时刻对应的是末制导的初始时刻，此时的运动状态主要包括拦截弹所在位置和其速度方向，这些状态将决定在末制导的初始时刻拦截弹是否处在有利的拦截阵位。下面对弹目相对运动模型进行讨论。

如图2所示，弹目相对位置矢量定义：

r=rT-rM=ρer

(13)

式中rM、rT分别为拦截弹和目标的位置矢量；er为沿弹目视线方向的单位矢量；ρ为弹目的相对距离。

弹目的相对运动速度与加速度可表示如下：

(14)

式中vM、vT、aM、aT分别为拦截弹与目标和速度与加速度。

弹目相对运动在三个方向分量上应满足：

(15)

弹目相对运动关系应满足：

(16)

式中aMt、aMr、aTt、aTr分别为拦截弹与目标的加速度沿er与et方向上的分量。

图2 弹目相对运动关系Fig.2 Relative movement of missile and target

3.2 基于PPN的捕获条件推导

纯比例导引律(PPN)是较为常用的一种比例导引改进制导律，其被广泛地应用在各种高精度的末制导律设计中。基于PPN推导中末制导交接班的约束条件，对于研究中制导律的终端弹道约束具有十分重要的意义。下面结合文献[18]，给出适用于临近空间拦截弹的捕获高速非机动目标的约束条件。

为便于描述拦截弹和目标在末制导段的初始运动状态对拦截的影响效果，做如下的定义：

(17)

(18)

式中 下标“0”为在末制导捕获时刻的状态；θvM0、θvT0分别为拦截弹速度指向与弹目视线、目标的速度指向与弹目视线的夹角。

通过分析弹目的几何关系可知，确定了θvM0、θvT0，结合目标的位置信息，就可确定拦截弹位置和速度指向(即弹道倾角)的初始状态。因此，研究捕获条件就是确定这两个变量的所要满足的约束条件。

定义拦截弹和目标的速度大小的比值：

p=VM/VT

相应地定义有效速度大小的比值：

基于PPN导引飞行，拦截弹捕获高速非机动目标(p<1)的条件：

(20)

其中

(21)

式中β为导航比；θc为在能够实现拦截的条件下，目标的初始速度方向与弹目视线方向的最大夹角。

具体计算过程：通过目标轨迹预测获得目标速度指向与目标位置信息，以目标为参考，即可获得θvT0的变化范围，根据导引头探测距离确定可行的拦截器位置变化范围，再由θvM0和弹目视线角范围可获得拦截器的速度指向变化范围。上述捕获区描述的是拦截弹捕获目标时弹目交会角所要满足的充分必要性条件。

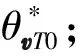
(21)

4 仿真算例

4.1 PPN的交接班捕获窗口定量描述

假定通过目标轨迹预测获得的目标速度为2250 m/s；拦截弹的平均速度为1500 m/s；通过计算可得目标与拦截弹速度比近似为p=0.67，选择β=4。采用第2.4节中推导的公式计算捕获区，可获得PPN的交接班捕获窗口，数据如表2所示。

上述PPN的交接班捕获窗口数据可转化为如图3、图4所示。

表2 中末制导交接班约束条件的特征点

图3 捕获窗口示意图Fig.3 Schematic diagram of capture window

图4 可拦截目标所在区域Fig.4 Interception area of target

由以上可知，在采用PPN拦截高速目标过程中，当目标速度指向与视线夹角θvT0为138.9°～221.8°时,可有效拦截目标，在端点处只有一个θvM0与之对应；当θvT0=176.8°时，拦截弹可选择的初始速度指向范围最大，拦截弹的初始速度的指向范围越大；当θvM0=-80.7°时，可拦截目标的初始速度指向范围最大。图3以目标为参考点，描述了末制导初始时刻拦截弹位置与速度指向的约束集合。图4是以拦截弹为参考点，描述了末制导初始时刻目标位置与拦截弹速度指向的约束集合。

由上述对交接班问题的分析可知，给定目标和拦截弹的速度比以及导航比，从几何关系上可对末制导捕获条件进行定量描述，得到实现交接班时弹目交会角所要满足的范围，为设计中制导终端约束条件提供依据。由于本节得到的捕获区窗口是中制导终端所要满足的一个必要条件，即角度满足约束才能顺利实现中末制导交接班。但具体的终端约束条件的设置还与拦截场作战景有关，根据高超声速目标的轨迹预测理论研究[19]，预测得到的目标轨迹实际上是一条管道，目标在某一时刻的预测位置实际上是一个范围，即目标在此时刻可能出现的区域。因此为了确保对目标的有效拦截，应采用多弹协同拦截的方式，借助多枚拦截弹对预测区域范围进行覆盖，并根据合理的任务分配计算单枚拦截弹预测命中点，进而计算预测交班点信息，确定各个拦截弹的终端约束条件。由于本文不涉及多弹协同拦截的任务分配、预测命中点及预测交班点信息的计算等内容，所以4.2节的仿真中直接给出预测交班条件。

4.2 弹道与导引律分离设计验证

垂直上升段的原则是保证拦截弹达到一定速度，以便开始控制。假定垂直上升段末端速度为500 m/s，高度达5000 m，转弯段以此状态为起点。由于本节验证分离设计的优化弹道的优势，所以这里直接给定中制导的终端位置约束为(250 000，30 000)，终端弹道倾角约束为-30°，采用高斯伪谱法优化[20]，仿真结果如图5所示。

图5 高斯伪谱法优化弹道Fig.5 Optimal trajectory by Gauss pseudospectral method

为说明弹道与导引律分离设计的优势，将基于高斯伪谱法的弹道与采用比例导引的弹道进行了比较，三种弹道的初始条件一致，仿真结果如图6、图7和表3所示。其中Gauss表示根据路径约束与预测交班信息，采用高斯伪谱法优化的弹道。PN-Target指基于目标运动参数，按照比例导引飞行，目标初始位置距拦截弹发射点615 km，以2250 m/s的速度在30 km高度上平飞，当弹目相距100 km时认为进入交接班过程，计算停止；PN-HP指将预测交班点作为目标位置，认为目标固定，拦截弹按照比例导引飞行。

图6 弹道对比Fig.6 Trajectory comparison

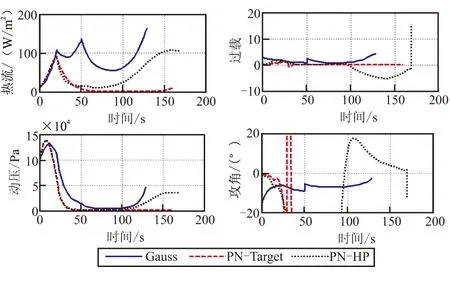
图7 弹道过程量对比Fig.7 Comparison of trajectory process variable

弹道t/sθf/(°)vf/(m/s)Gauss128．5-302179．5PN⁃Target159．7-41．762114．8PN⁃HP169．3-0．261887．8

由图6、图7和表3可知，按照本文助推方案设计，三种弹道都为先爬升而后下降的过程。PN-Target弹道在中末制导交接班时相对目标的位置和速度指向，都是由制导律本身决定的，无法按照前述终端约束条件的要求，在交接班时刻实现对拦截弹位置和弹道倾角的控制，也就无法保证进入末制导时，拦截弹处于较为有利的阵位，且其飞行高度较高，导致飞行时间较长。若对中制导终端位置进行控制，即PN-HP弹道，其飞行时间增加，末速降低，不利于拦截作战。由弹道过程量对比可知，三种弹道动压、过载区别不大，基于高斯伪谱法的弹道的热流密度相对于比例导引弹道较大，主要由于其在临近空间下层以相对高速飞行造成。从控制量的角度看，基于高斯伪谱法的弹道全程攻角较小，而比例导引弹道全程攻角接近最大值，导致较大能量损耗，且存在大范围跳变，控制上难以实现。

5 结论

(1)本文结合目标特性分析，基于弹道与导引律分离原则设计了高抛再入弹道方案，建立了弹道优化模型，研究了中末制导交接班的条件，从而为完善拦截弹终端约束模型提供了参考。仿真结果表明，本文设计的弹道能够对终端位置和弹道倾角进行控制，且飞行时间短、末速较大，是较为理想的拦截弹道。

(2)本文只考虑了单枚弹的弹道设计问题，为确保对目标的有效拦截，应采用多弹协同拦截的方式，后续研究应考虑多枚拦截弹对预测区域范围进行覆盖，并根据合理的任务分配计算单枚拦截弹预测命中点，进而计算预测交班点信息，确定各个拦截弹的终端约束条件。

参考文献：

[1] Bertin J J,Cummings R M.Fifty years of hypersonics:where we’ve been,where we’re going[J].Progress in Aerospace Sciences,2003,39:511-536.

[2] 冯志高,关成启,张红文.高超声速飞行器概论[M].北京:北京理工大学出版社,2016.

FENG Zhigao,GUAN Chengqi,ZHANG Hongwen.An introduction to hypersonic aircraft[M].Beijing:Beijing Institute of Technology Press,2016.

[3] 孙磊,黄可西,常晓飞,等.临近空间高超声速巡航导弹拦截问题研究[J].西北工业大学学报,2015(4):615-620.

SUN Lei,HUANG Kexi,CHANG Xiaofei,et al.Researching Interception of Near Space Hypersonic Cruise Missile[J].Journal of Northwestern Polytechnical University,2015(4):615-620.

[4] 金欣,梁维泰,王俊,等.反临近空间目标作战的若干问题思考[J].现代防御技术,2013,41(6):1-7.

JIN Xin,LIANG Weitai,WANG Jun,et al.Discussion on Issues of Anti-Near-Space-Target Operation[J].Modern defense technology,2013,41(6):1-7.

[5] 魏倩,蔡远利.J2项摄动影响下的大气层外弹道规划改进算法[J].控制理论与应用,2016,33(9):1245-1251.

WEI Qian,CAI Yuanli.Trajectory planning algorithm of exo-atmosphere aircraft under the influence of the J2 perturbation[J].Control Theory & Applications,2016,33(9):1245-1251.

[6] 魏倩,蔡远利.一种基于神经网络的中制导改进算法[J].西安交通大学学报,2016,50(7):125-130.

WEI Qian,CAI Yuanli.A Modified Algorithm on the Midcourse Guidance Based on BP Neural Network[J].Journal of Xi’an Jiaotong University,2016,50(7):125-130.

[7] Shaul G,Sergey R.Exo-atmospheric mid-course guidance[C]//AIAA Guidance,Navigation and Control Conference.New York,USA,2015:2015-0088.

[8] BT 斯维特洛夫.防空导弹设计[M].北京:宇航出版社,2004.

Светлов В Г.Air defense missile design[M].Beijing:Chinese Astronautics Press,2004.

[9] 李宁波,雷虎民,谭诗利,等.基于虚拟域动态逆的空地反辐射导弹轨迹优化[J].弹道学报,2016,28(4):7-11.

LI Ningbo,LEI Humin,TAN Shili,et al.Trajectory optimization for air-to-ground ARM based on inverse dynamics in the virtual domain[J].Journal of Ballistics,2016,28(4):7-11.

[10] Lu P,Forbes S,Morrgan B.Gliding guidance of high L/D hypersonic vehicles[R].AIAA 2013-4648.

[11] Steven H W,Col J S,Dale S.The DARPA/AF falcon program:The hypersonic technology vehicle #2(HTV-2)flight demonstration Phase[R].AIAA 2008-2539.

[12] LI Ningbo,LEI Humin,ZHOU Jin,et al.Variable-time-domain online neighboring optimal trajectory modification for hypersonic interceptors[J/OL].International Journal of Aerospace Engineering,2017,doi:10.1155/2017/9456179.

[13] 赵杰,王君,张大元,等.反临近空间高超声速飞行器中末交接视角研究[J].飞行力学,2015,33(3):253-256.

ZHAO Jie,WANG Jun,ZHANG Dayuan,et al.Visual angle research for midcourse and terminal guidance hand-over of near space hypersonic vehicles[J].Flight Dynamics,2015,33(3):253-256.

[14] 李新国,方群.有翼导弹飞行动力学[M].西安:西北工业大学出版社,2005:153-155.

LI Xinguo,FANG Qun.Flight dynamics of winged missile[M].Xi’an:Northwestern Polytechnical University Press,2005:49-50.

[15] Peter J Mantel.The missile defense equation:factors for decision making[M].AIAA,2004.

[16] Afshin R,Krishna D K,Hekmat A.Particle swarm optimization applied to spacecraft reentry trajectory[J].Journal of Guidance,Control,and Dynamics,2013 36(1):307-310.

[17] 樊会涛.复合制导空空导弹截获目标概率研究[J].航空学报,2010,31(6):1225-1229.

FAN Huitao.Study on Target Acquisition Probability of Air-to-air Missiles with Combined Guidance[J].Acta Aeronautica et Astronautica Sinica,2010,31(6):1225-1229.

[18] Feng Tyan.Analysis of 3D PPN guidance laws for nonmaneuvering target[J].IEEE Transactions on Aerospace and Electronic Systems,2015,51(4):2923-2934.

[19] 翟岱亮,雷虎民,李炯,等.基于自适应IMM的高超声速飞行器轨迹预测[J].航空学报,2016,37(11):3466-3475.

ZHAI Dailiang,LEI Humin,LI Jiong,et al.Trajectory prediction of hypersonic vehicle based on adaptive IMM[J].Acta Aeronautica et Astronautica Sinica,2016,37(11):3466-3475.

[20] LI Ningbo,LEI Humin,SHAO Lei,et al.Trajectory optimization based on multi-interval mesh refinement method[J/OL].Mathematical Problems in Engineering,2017.doi:10.1155/2017/8521368.