基于效用最大化问题和马科维茨模型的婚姻的讨论

高雁南

(山东女子学院，山东 济南 250300)

用经济学思想研究婚姻问题，是一件很有创造力的事情，也是一件顺理成章的事情。德国社会学家L·穆勒认为结婚有3个主要动机：经济、子女和爱情。从这个角度来看，用经济学的观点研究婚姻是有效并且有趣的。1973年美国经济学家Gary Becker使用效用最大化的思路解释婚姻问题，发表了《婚姻理论I》的文章，标志着用经济学研究婚姻正式成为现实[1]。本文部分借助了Becker的效用最大化的思想，但是并没有使用Becker的效用函数；同时还使用了马科维茨的资产选择模型分析了青年男女走进婚姻殿堂的两个动因，为婚姻选择提供了经济学的解释。

一、婚姻选择问题的假设

由于现代婚姻是男女双方共同自愿达成的，现代社会包办婚姻的情况已经不多，父母虽然会在子女的婚姻中提出参考意见，但是父母的意见绝大多数情况下仅供子女参考，因此父母在子女婚姻中起的作用就是提出建议，例如子女对婚姻中的一些因素未考虑到而经父母的提醒注意到后，最终可能会改变对配偶的选择，可是无论怎样，决定是由子女独立作出的。基于婚姻自愿的原则，可以使用经济学中的偏好(Preference)的概念去刻画男女双方对婚姻的选择，而偏好对应的是效用，也就是说，男女双方是否选择进入婚姻，取决于他们结婚之后的生活是否出现了改善，也就是他们的效用是否提高了。

男女在结婚之前，各自保持单身，而结婚之后，他们的收入会合并，消费也因此会合并。不难发现，结婚之后夫妻双方的消费合并对夫妻的生活质量有较大的提高，这可以表现在有相当多的生活耐用品夫妻是可以共用的，所以在较小的消费支出下，夫妻消费可以达到较高的效用，例如房产，夫妻双方只要投入一套房产的钱就可以获得很高的效用，而如果他们不结婚，就不得不每人支出一套房产的消费，从而使他们各自持有的存款或金融资产的比例降低。根据经典的效用理论，一个消费者的效用取决于他的消费，这在某些情况下是有道理的，可是，在家庭和婚姻的这个范畴中，较高的消费并不总是能够带来较高的效用。应该指出的是，在保证消费一定的情况下，尽可能地保留更多的金融资产对个人未来的保障是最重要的，即使剩余的金融资产并没有完全变成消费，它们也完全可以通过遗产的方式保留给下一代，从而维系整个家族和下一代的财富水平。这种观念在东亚地区尤其是中国是主流思想，传统的宏观模型中总是假设住户在最后一期将所有的资产变成消费，为的是将以消费作为主要自变量的效用函数最大化。因此，建立以金融资产为主要自变量的效用函数是该模型的又一个重要假设。在这里，金融资产指的是那些投资回报率高、风险低的高保值、高增值财产，包括优质金融产品、房产、分红保险等。

需要注意的是，由于金融资产是不断累积的，第一期的收入减去消费之后是第一期的金融资产，而第一期的金融资产经过增值之后会与第二期的收入合并用于第二期的消费，同样的，第二期消费完毕之后剩余的金融资产(也可能包含第一期的一部分)将继续在第三期进行增值用于第四期的消费。由于金融资产的累积效应，同时考虑到消费者可能会在生命的前半期通过借贷的方式进行消费，所以在最大化效用函数的时候只要取较为末期的金融资产余额作为自变量即可，此时对应的消费者已近中年，已经具备了相当的财务能力，有的已经实现了财务自由，比如，取第n期的金融资产。

二、效用最大化分析

假设一个住户有x个家庭成员，当x=1时，即对应单身，当x大于等于2时，就对应着已婚的情况，此处假设x只能取1或2，需要指出的是，此时分析的更多的是青年男女在结婚时候的选择，而对于子女的诞生对住户效用的影响暂且不作分析。

先假设x=1，此时住户中只有一个单身成员，假设这名单身成员可以活X期，第一期开始单身成员找到了工作取得工资，假设该名单身成员在未来任何一期都不会失业，都能取得工资，设其工资收入为M，则第一期的工资收入为M1；设他的消费为C，则第一期的消费为C1；将其剩余的金额作为金融资产，记为A1，则很容易写出住户第一期的预算约束(Budget constraint)：

A1=M1-C1

(1)

依次写出住户第2期、第3期、第4期的预算约束：

A2=A1(1+r)+M2-C2

(2)

A3=A2(1+r)+M3-C3

(3)

……

An=An-1(1+r)+Mn-Cn

(4)

将(1)式代入(2)式，得到

A2=M1(1+r)+M2-C1(1+r)-C2

(5)

将(4)代入(3)得到，

A3=M1(1+r)2+M2(1+r)+M3-C1(1+r)2-C2(1+r)-C3

(6)

根据以上方法逐次迭代，可以得到An的表达式：

(7)

想要最大化住户的效用，也就是最大化An，就要使Mt尽可能地大，Ct尽可能地小，也就是说住户尽可能地获取更高的收入，在保证正常消费的情况下，尽可能减少浪费性或者不保值的产品的购买，例如不保值且养护成本较高的豪华轿车。

(8)

造成消费减少的原因有如下几个方面：

第一，生活用品尤其是大型耐用品可以共同使用，实现资源优化，从而极大地减少开支，比如汽车，夫妻双方购买一辆即可满足日常出行；比如房子，夫妻双方只要共同负担一套房子的支出就可以保证正常的生活质量。除了有代表性的大件生活用品外，日常生活的必需品都可以共用，比如电费、水费、煤气费、网费都可以不再重复支出，从而节省大量开支。

第二，资源利用效率提高可以避免浪费，例如在食品开支上，单身的男女更多的是选择外出就餐或者是自己做饭，自己做饭的时候由于一人做饭能源的利用效率较为低下，同时可能会造成浪费，而两个人拼火做饭，则会显著降低个体食品支出成本。

所以，合并之后，两个人的消费支出有可能不升反降，个体消费支出则会出现较大可能的下降。夫妻双方可以在保证收入至少不变的情况下，调整夫妻二人收入来源的分配，也就是二者在家庭中的分工，比如丈夫如果找到了较为高薪的工作，那么妻子就可以适当减少工作时间，从而照顾家庭，夫妻之间的劳动工时可以极大程度地互相替代。

另外一个值得注意的方面就是金融产品的利率r往往会随着投资基数的增加而增加，例如许多金融理财产品在投资的时候都有最低认购限额，两人财务合并之后，能够获得更大的投资基数，所以有可能会获得更高的投资回报率。

从上面的分析可以看出，结婚从某种程度上有一种“规模效应”的结果，能够降低生存成本、提高生活质量，从而获得更高的幸福感。

三、从另一个角度讨论婚姻对于收入的影响

通过上面预算约束的分析发现，住户能否实现更大的幸福感，取决于他是否能够获得更多的收入并在最大程度上积累更多的财富，而由于收入的取得存在着波动性，没有人能够保证一生工资无忧且一直保持稳定，所以收入的波动性可以用风险这个金融学的概念衡量，住户的目标是不仅仅要获得较高的期望收入，更要尽可能地减小收入风险，这跟金融学中的马科维茨资产组合模型中探讨的问题几乎完全一样。马科维茨(1952)创造性地使用了均值-方差组合模型选出了他认为最佳的投资组合[2]，类似地，我们可以借用马科维茨的资产组合模型对婚后收入合并对收入风险的控制进行说明。

马科维茨模型中的单个证券的收益率，就可以被刻画成单个单身男性M的收入，单个证券的期望收益率对应着单身男性的期望收入。假设单身男性的收入服从下面的伯努利分布：

收入状态收入大小概率高aμ低b1-μ

同样单身女性F的收入就相当于投资组合中的另外一个证券，单身女性的收入也服从一个伯努利分布：

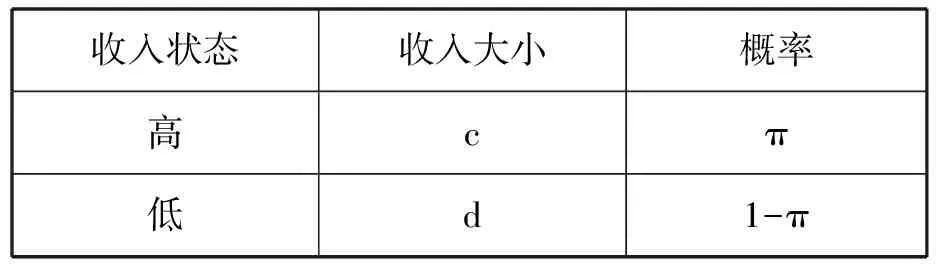
收入状态收入大小概率高cπ低d1-π

单身男性M的收入的数学期望可以写成：

E(M)=aμ+b(1-μ)

(9)

单身女性F的收入的数学期望可以写成：

E(F)=cπ+d(1-π)

(10)

根据标准差的定义，单身男性M的收入的标准差可以写成：

(11)

同理单身女性F的收入的标准差可以写为：

(12)

假设结婚之后，男性在家庭总收入中所占的比例为QM，女性在家庭总收入中所占的比例为QF，则容易得到：

(13)

(14)

QM+QF=1

(15)

婚后男女的期望收入为：(用H表示婚后总收入)

E(H)=QME(M)+QFE(F)

婚后男女收入的标准差的公式可以通过综合上面的公式证明(证明略去)，为：

(16)

其中σMF是单身男女收入的协方差(σMF=E[M-E(M)][F-E(F)]),容易证明协方差可以写成单身男女各自收入的相关系数和它们各自收入标准差的乘积：

(17)

其中ρMF为两人收入的相关系数。

通过上面的公式我们可以看到：夫妻双方的收入相关性越小，收入组合的波动越小，风险就越小。这可以解释婚姻选择市场上大家普遍不愿意寻找与自己相近职位或同一行业的伴侣，因为这不利于收入风险的规避。

类似的还有，为什么寻找伴侣的时候大家都愿意找工作稳定的？首先从相关性上来看，假设配偶的工作绝对稳定，意味着自己的工作与配偶的工作无任何相关性，则相关系数为零，即ρMF=0。其次，配偶的工作稳定对应着配偶收入的标准差为零(QF2σF2=0)，那么夫妻双方收入的标准差就变成：

(18)

显然在这个例子中的男方愿意找一个工作收入比自己稳定的女方来抵消自己收入的风险。这就不难理解，为什么男性特别喜欢寻找教师、公务员等稳定职位的女性作为自己的配偶了。

再来看另外一个例子，如果男性和女性从事的工作在不同的行业，收入的变化成负相关，那么从合并收入的标准差公式很容易看出，男女的收入的相关系数越小，合并后的收入的标准差越小，2QMQFσMσFρMF对应地就越小，σH也就越小。

如果假设男性和女性收入的相关系数为-1，即为完全负相关，那么能否确定一个固定的QM、QF使得两人合并收入的标准差最小呢？为了便于记录，设QM=q，则QF=1-q，ρMF=-1，则容易写出σH2的表达式：

σH2=q2σM2+(1=q)2σF2-2q(1-q)σMσF

(19)

对(19)求导，可得最小的q为(可证二阶条件大于零)：

(20)

将q*带回(19)中，易得到：

σH=0

同时，也可以写出男女在这种情况下的平均收入：

(21)

这是最令人欢喜的结论，因为在比较严苛的假设下，男女双方可以通过合并收入的方式把收入波动的风险降到0，当然这也大大低于男女单身时各自面对的收入波动的风险。

需要特别指出的是，风险一味降低也并不是一件好事，因为那可能意味着以两人收入的大幅度降低作为标准代价，在收入较高的情况下保持相对较低的标准差才是理性的选择。在这里笔者使用马科维茨模型并不是要真的确定夫妻双方的收入期望值和波动性，并且这也并不是主观上能够确定的，使用这一理论只是想说明，结婚可以使夫妻双方收入的波动整体降低，从而从金融学的角度论证结婚可以降低收入波动风险这一论断。

四、总结

经济学可以为婚姻问题提供很多有趣的解释，通过效用最大化问题和马科维茨模型对婚姻选择的解读，可以得到如下启示：

第一，婚后的收入合并可以有效地增加夫妻双方金融财富的积累，从而使夫妻双方更有幸福感，这一结论的得出是基于对三个事实的分析：一是结婚可以减少个体消费，产生规模效应，降低生活成本；二是结婚可以合并收入，集中力量办大事；三是结婚可以增加用于投资的金融资产的基数，从而获得更大的投资回报率。

第二，婚后的收入合并可以降低收入的波动，从而使生活更加稳定，考虑到大多数人都是风险厌恶者，婚姻可以有效规避风险，从而增强夫妻双方的幸福感。

第三，上述分析中并没有牵扯到举办婚礼的投入对夫妻双方消费的影响，显然，在中国的传统风俗下，婚姻的缔结需要支出相当的费用，包括婚礼费用、婚后生活用品的采购等，撇开婚礼费用之外，其余大量商品的采购是为日后生活进行的必需采购，并没有额外增加夫妻双方的消费。此外，大多数情况下，婚礼的费用支出大部分都由年轻人的父母承担，同时，为举办婚礼支出理性的、可接受的费用，已经成为大多数理性消费者的选择。因此，婚礼费用不会对婚后夫妻的消费行为产生太大牵绊。

第四，子女的生养对婚后消费的影响在本文中并没有给出相关分析，显然，养育子女会极大程度地增加婚后的家庭消费，考虑到生养子女是绝大多数中国家庭的选择，即使没有选择立刻结婚的青年也会为自己未来子女养育积累更多的资本，而这种资本的积累恰恰在婚后会更加迅速，因此，通过结婚的方式积累更多的财富从而为生养子女作准备，亦可以作为上述分析对婚姻选择的解读。

第五，对于选择金融资产数量的多少作为决定消费者效用的自变量，会引起如下的思考：现时对于金融资产的积累实际上是一种储存起来的未来消费，因此，金融资产的多寡影响的是未来的消费——影响的仍然是消费。对于这种思考有两方面的回应：一是为什么中国消费者一直以来保持较高的储蓄率，且年轻一代的储蓄率并不比年长一代更低？二是财富的代际转移是不是使更多的人把积累更多的金融资产作为延续家族繁荣和获得幸福感的重要因素？这都是可以进一步进行分析和研究的。

青年男女之所以选择走入婚姻殿堂是受多种因素决定的，这涉及社会科学和自然科学的各个方面，本文主要从经济学的两个大的角度对婚姻的选择给出了相关解释。希望通过这些解释，能够使大家更好地了解婚姻，选择婚姻，并拥有美满幸福的人生。

参考文献:

[1] Markowitz H.PortfolioSelection[J]. Journal of Finance, 1952,7(1):77-91.

[2] Becker G S.ATheoryofMarriage:PartI[J]. The Journal of Political Economy, 1973,81(4):813-846.