连廊设计对非对称高层结构地震响应影响
董彦杰
(厦门船舶重工股份有限公司 福建厦门 361026)
0 引言
随着建筑结构形式的多样化发展,带连廊的非对称高层结构日益涌现,连廊结构的地震响应分析成为研究的热点问题。由于结构具有独特的性质,很难用统一的理论去分析不同的建筑结构,因此,有必要对具体工程进行具体分析。包世华[1]等采用分段连续简化方法建立了某连廊结构模型,并通过理论推导结构水平方向振动微分方程,通过软件解微分方程求解结构自振周期和振动模态。卞朝东[2]等推导了对称结构和非对称结构的振型参与系数分量形式,提出在对复杂连廊结构进行地震响应分析时,应选取足够多的振型数量才能满足计算精度要求。Raul[3]将连廊简化为弹性变形梁,建立符合刚片系模型,对某带连廊的砌体结构进行了地震响应分析。
对不同的实际工程案例,有必要分析各参数变化对结构振动的影响,以达到优化设计,保证结构安全的目的。王吉民[4]等基于连廊为弹性梁的假定,探讨了连廊刚度改变对整体结构振动模态和抗震性能的影响。王克峰[5]等从理论上提出了一种考虑大跨度结构行波效应后的反应谱简化计算方法,只需通过调整振型参与系数,即可简单考虑结构的行波效应。黄坤耀[6]等将连廊简化为弹性梁,采用时程分析法探讨了不同工况下整体结构的地震响应。侯家健[7]等则对某双连廊结构进行弹塑性地震响应分析,根据模型分析结果对工程项目进行评估,并提出了加固方案。文献[8-9]对几个实际工程案例(上海交银金融中心大厦、北京星城广厦和马来西亚佩重纳斯大厦)进行了建模分析。
高层非对称连体结构在设计中需考虑的因素较多,如连廊结构连接方式和连廊设计位置均会对整体结构抗震性能产生较大影响。因此,本文基于工程设计模型,采用弹性时程分析法,对比分析了连接方式和连廊位置对结构地震响应的影响。
1 工程背景及有限元模型的建立
该工程背景为某框架剪力墙结构的办公楼项目,占地面积约2.4万m2。项目包括5栋办公楼,其中1号楼与2号楼之间采用连廊结构(钢结构桁架)。两栋楼的框架柱截面尺寸为800mm×800mm,框架梁为400mm×600mm,剪力墙厚为300mm。首层层高均为4.2 m,二层以上各层层高为3.3m。1号楼为地上28层,2号楼地上22层,连廊位于第十三层和十五层之间,连廊桁架柱采用H500×300×12×20,桁架梁采用H400×300×10×16,桁架斜腹杆采用□200×200×20。该建筑的结构设计年限为50年,安全等级二级,抗震设防烈度为8度,设计基本地震加速度为0.2g,场地类别为II类。
利用有限元软件SAP2000建立三维空间模型如图1所示,模型共包括1751个节点,3363个框架单元,1227个面单元。

图1 三维有限元模型
2 动力特性分析
对模型进行动力特性分析,计算结果如表1所示。从表1可以看出,结构第一阶扭转周期与第一阶平动周期之比为0.66,满足规范要求的复杂高层结构第一阶扭转周期与第一阶平动周期之比不能大于0.85的要求,说明该结构刚度分配合理,结构振型符合建筑设计要求。

表1 结构前8阶振型和质量参与系数
注:UX表示X向的质量参与系数;UY表示Y向的质量参与系数;RZ表示绕Z向的质量参与系数。*表示振动幅度较小。
3 参数变化对结构地震响应的影响分析
3.1 输入时程曲线
根据工程背景抗震设防基本信息,选择El-Centro波、Taft波和一条人工波进行时程分析,3条波的时程曲线如图2所示。并根据要求对3条波进行峰值调整,调整系数分别为0.2048、0.4584和6.667。

(a) El-Centro波时程曲线

(b)Taft波时程曲线
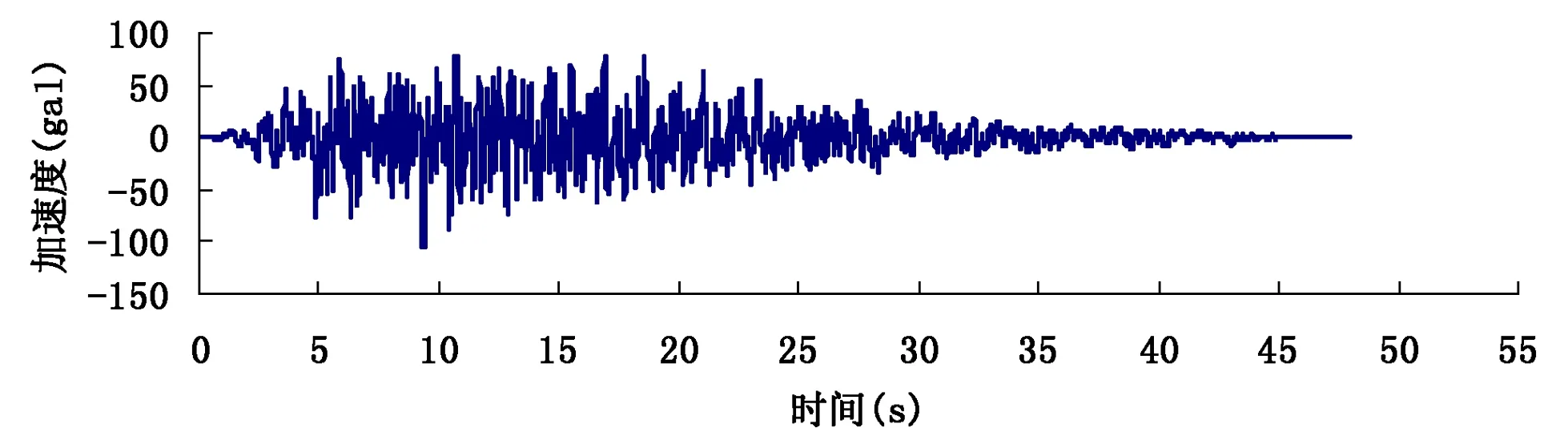
(c)人工波时程曲线图2 输入的时程曲线图
3.2 连接方式变化对结构地震响应的影响分析
该工程中连廊为钢结构,与两侧塔楼可采用刚性连接或铰接两种方式。将连廊设于13~14层位置,分别建立“铰接模型”和“刚接模型”,采用时程分析法,对比分析两种模型的地震响应。
为明确连接方式对结构地震响应的影响,忽略结构扭转效应的影响,分别提取两塔楼顶层固定的两个节点计算结果。两种模型在不同地震波作用下的结构顶层最大位移值如表2所示。从表2中可以看出,在3条不同地震波作用下,连廊连接方式改变对结构整体刚度几乎没有影响,结构顶层位移值变化微小(小于0.5%),基本可以忽略不计。
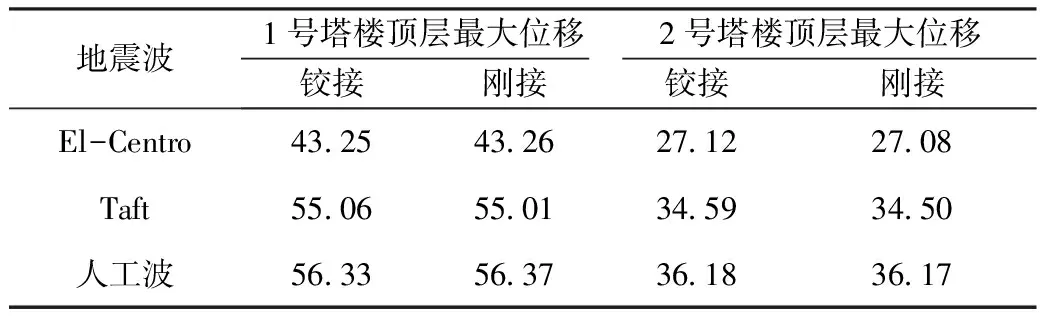
表2 不同连接方式下顶层最大位移 mm
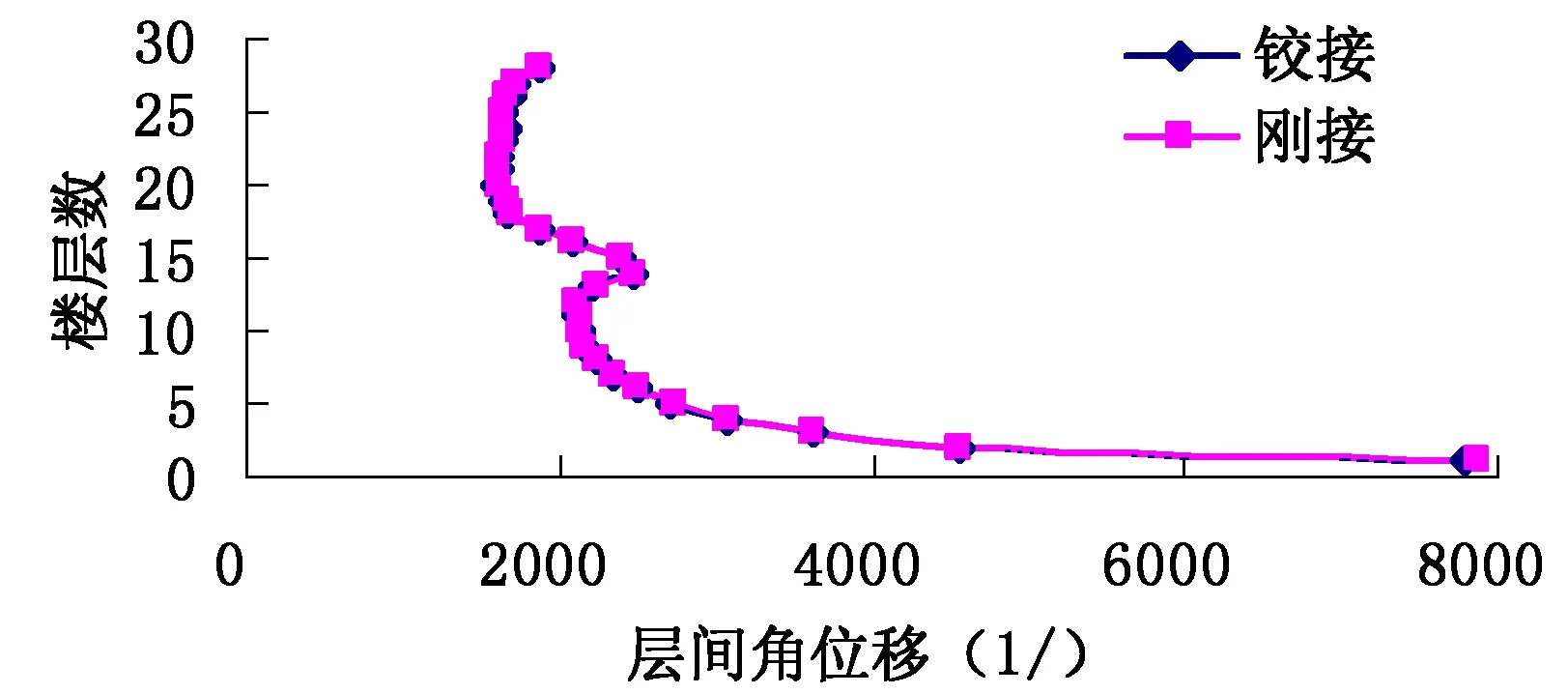
(a)El-Centro波
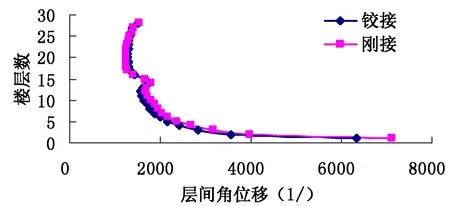
(b)Taft波

(c)人工波图3 不同连接方式下1号塔楼各层层间位移角
图3~图4给出了不同连接方式下,两侧塔楼层间位移角随楼层高度变化的曲线。从图中可以看出:对1号塔楼而言,El-Centro波作用下,两种连接方式基本没有影响;在Taft波作用下,采用铰接时连廊下部楼层层间位移大于刚接模型,连廊上部楼层层间位移则相反;人工波作用下连廊连接方式对地震响应的影响规律与Taft波作用下相反,且两种模型的层间位移角均小于规范限制。对2号塔楼来说,El-Centro波作用下,两种连接方式基本没有影响;在Taft波作用下,采用铰接时,除连廊所在位置外,其余楼层层间位移均大于刚接模型;人工波作用下连廊连接方式对地震响应的影响规律与Taft波作用下相反。同时,两种模型的层间位移角均小于规范限制。

(a)El-Centro波

(b)Taft波

(c)人工波图4 不同连接方式下2号塔楼各层层间位移
通过计算发现,连廊的上梁最大剪力大于下梁最大剪力,因此表3仅列出了不同连接方式下,连廊跨中最大弯矩和上梁最大剪力。从表中可知,对不同地震波作用,连接方式对连廊地震响应的影响规律一致。连廊铰接时,跨中弯矩和上梁最大剪力均大于刚性连接模型。从连廊内力角度考虑,设计中宜优先采用铰接方式。
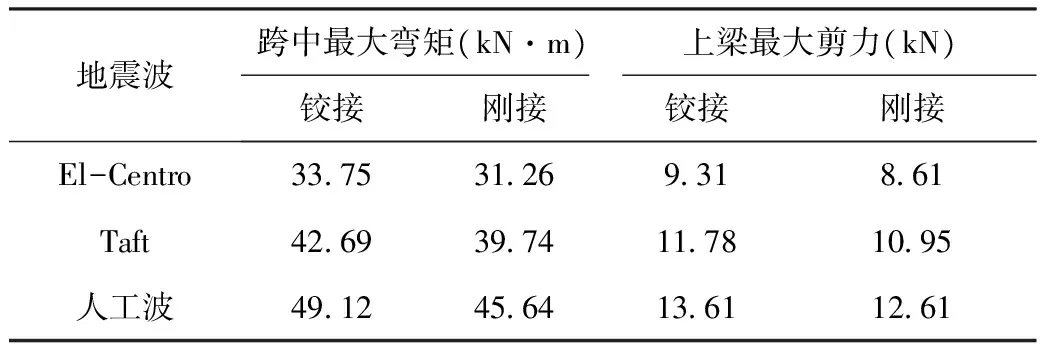
表3 不同连接方式下连廊内力
表4列出了不同连接方式下整体结构的基底反力。可知,在El-Centro波和Taft波作用下影响规律一致,采用铰接时基底剪力和倾覆弯矩均小于刚接模型。在人工波作用下,铰接模型基底剪力和倾覆弯矩均大于刚接模型。通过取3条波平均值对比可以看出,采用铰接时结构基底反力会略小于刚接模型,设计中可优先考虑铰接模型。
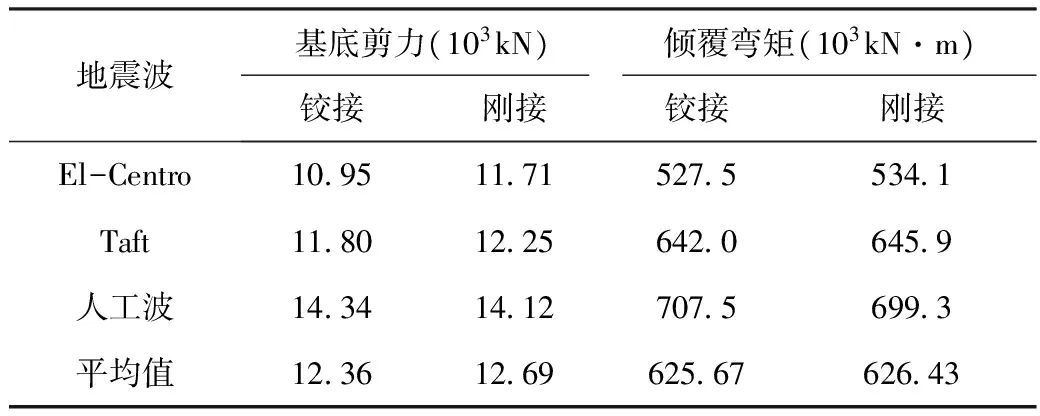
表4 不同连接方式下结构基底反力
综合来看,连廊连接方式对结构整体地震响应影响较小,但从结构优化设计角度来看,可优先考虑采用铰接方式连接连廊与塔楼。
3.3 连廊位置变化对结构地震响应的影响分析
根据3.2分析结果,确定连廊与塔楼之间采用铰接。为分析连廊位置对整体结构的影响,共设置了3种方案:(1)连廊设在6~7层位置,简称为“位置一模型”;(2)连廊设在13~14层位置,简称为“位置二模型”;(3)连廊设在21~22层位置,简称为“位置三模型”。
对比分析3种工况下顶层最大位移(计算结果见表5)可知,在3条地震波作用下,连廊位置对1号塔楼结构响应的影响规律一致,随着连廊位置的增高,顶层最大位移逐渐减低。这是由于连廊高度越高,对结构顶层自由端的约束就越大,因此侧向位移就越小。2号塔楼在Taft波和人工波作用下,顶层位移随着连廊高度的增大而增大,这是因为连廊高度越高,2号塔楼受1号塔楼侧移影响越大导致。在El-Centro波作用下,连廊设在13~14层位置时,顶层位移最小。从3条地震波平均值结果来看,连廊位置越高对1号塔楼越有利,连廊位置在中间时,对2号塔楼较有利。

表5 连廊位置不同时顶层最大位移 mm
图5~图6绘制了连廊位置变化时两侧塔楼层间位移角随楼层高度变化的曲线。从图中可以看出,连廊位置的改变对层间位移和位移角的影响较大,连廊的设置会大大减少两侧塔楼的层间位移。对1号塔楼而言,当连廊设置在21~22层时,在任何一条地震波作用下,15层以上楼层的层间位移都较小;当连廊设置在6~7层时,在任何一条地震波作用下,10层以下楼层的层间位移都较小。3种模型的层间位移角均小于规范限制。对2号塔楼而言,不同地震波作用下,连廊位置的影响规律各不相同,具有较大的离散性。3种模型的层间位移角均小于规范限制。

(a)El-Centro波

(b)Taft波

(c)人工波图5 连廊位置不同时1号塔楼各层层间位移角

(a)El-Centro波

(b)Taft波

(c)人工波图6 连廊位置不同时2号塔楼各层层间位移
表6列出了不同连廊位置工况下,连廊跨中最大弯矩和上梁最大剪力值。从表中可知,对不同地震波作用,连廊设置位置对连廊地震响应的影响规律一致。连廊在13~14层时,跨中弯矩和上梁最大剪力值都最大;连廊设在6~7层时,跨中弯矩和上梁最大剪力值都最小。从连廊内力角度考虑,设计中宜优先考虑将连廊设在低楼层位置。
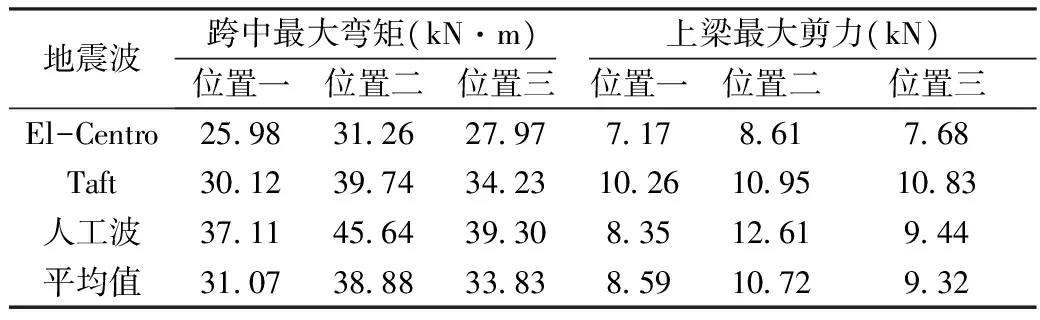
表6 连廊位置不同时连廊内力
表7列出了不同连廊位置工况下整体结构的基底反力。从表中可知,随着连廊位置高度的增加,结构基底剪力和倾覆弯矩均有增大趋势。这是由于连廊位置越高,地震波作用下的加速度峰值越大,由连廊振动引起的结构基底剪力就越大,倾覆弯矩也就越大。因此,在防震设计中应考虑将连廊设在低楼层位置。

表7 连廊位置不同时结构基底反力
综合来看,从控制结构顶层侧移角度考虑,宜将连廊设置在较高楼层位置。从控制结构振幅、连廊内力和基底反力角度考虑,则应考虑将连廊设在低楼层位置。
4 结论
通过采用时程分析法,分析多遇地震作用下连廊连接方式和连廊设计位置变化对地震响应的影响,得到以下结论:
(1)连廊连接方式对结构整体地震响应影响较小,但从结构优化设计角度来看,可优先考虑采用铰接方式连接连廊与塔楼。
(2)从控制结构顶层侧移角度考虑,宜将连廊设置在较高楼层位置。从控制结构振幅、连廊内力和基底反力角度考虑,则应考虑将连廊设在低楼层位置。在设计过程中应根据功能需要和受力特点综合考虑连廊位置。
参考文献
[1] 包世华,王建东.大底盘多塔楼连体结构的振动计算和动力特性[J].建筑结构,1997(6):40-44.
[2] 卞朝东,李爱群,娄宇,等.高层连体结构振型及其参与系数的分析[J].建筑科学,2002(4):20-24.
[3] Raul D B, Vitelmo V B. Performance-based seismic engineering: the need for a reliable conceptual comprehensive approach[J]. Earthquake engineering and structural dynamics, 2002(31):627-652.
[4] 王吉民,黄坤耀,孙斌楠.连体刚度和位置对双塔连体高层建筑受力性能的影响[J].建筑结构学报, 2002,22(3) :15-21.
[5] 王克峰,李静斌,丁洁民.连体结构行波效应的反应谱分析方法[J].郑州大学学报(工学版),2006(1):19-23.
[6] 黄坤耀,孙炳楠,楼文娟.连体刚度对双塔连体高层建筑地震响应的影响[J].建筑结构学报,2001(3):21-26.
[7] 侯家健,李桢章,韩小雷,等.双塔连体超高层建筑结构连接方案比较[J].工程抗震与加固改造,2006(6):81-84.
[8] 梁淑萍.大底盘双塔结构体系设计应用探讨[C]//第十七届全国高层建筑结构学术会议论文集,2002:150-154.
[9] 常林润.星城广厦大底盘多塔楼结构设计[J].建筑结构,2005,35(5):22-29.

