基于Bayes理论现场点荷载强度的判断

彭 杰

(珙县宏能芙蓉煤矿有限责任公司, 四川 宜宾市 644500)

0 引 言

岩体是一种变异性很大且不稳定的介质，是受环境影响较大的非均质各向异性体。采矿、隧道等各种地下空间的建设都是在岩土体中进行的，在进行施工前，都必须要详细准确的了解不同环境下岩石力学参数和岩体力学参数。然而，岩石作为非均质的复杂介质，要想获得精确的岩石力学参数比较困难，特别是随着采矿行业的发展，逐渐进入深部采矿作业，面临复杂的环境，为岩石力学试验的取样带来了很大的困难，不仅仅是费用高，且实验周期比较长。为了能方便的获取现场原位岩石的强度参数，必须进行现场岩石强度实验。现场点荷载强度测试的应用与推广为现场原位的强度参数测定提供了技术支持。但是，由于现场点荷载强度的试验样品是现场随机拾取的，并且试验数量有限，造成实验结果随机性和不稳定性很大，因此为了确定现场点荷载试验结果的可靠性，本文利用已有的实测数据获得岩石现场点荷载强度的概率分布，对小样本数据进行Bayes方法优化，以提高现场点荷载强度测试结果的可靠性和准确性[5-8]。

随着Bayes理论在岩土工程方面的广泛应用，众多学者也进行了这方面的研究。严春风[1]等人应用Bayes理论在有限的小样本前提下有效的解决了岩石力学参数概率分布的优化问题。毕忠伟[2]等人应用Bayes理论在少量的样本数据前提下，利用验前信息对岩石力学参数进行Bayes估计,并首先对其进行可信度研究。邓建[3]等人指出,破坏性试验必须运用序贯分析方法或者Bayes方法确定可靠性。闫春岭[4]从Bayes计算原理出发，结合岩石抗压强度分布的已有信息，随机抽取小样本数据，得到了岩石抗压强度后验分布统计量的计算公式，并进行了工程检验。笔者结合相关现场实验数据，应用Bayes方法来判断现场点荷载强度的概率。

1 Bayes统计原理[4]

Bayes统计学将未知的参数看作随机变量,并且认为在获得样本数据前也已存在一个概率分布,即验前分布[9]。样本数据下未知参数的分布称为后验分布, 后验分布是对未知参数统计推断的依据，因此Bayes方法用于估计某随机变量的参数，可基本解决样本容量有限的问题[9]。本文对后验概率密度进行理论计算。

假设现有现场测试样本A1，A2，…，An出自于未知的整体样本A，并设F(ai，Q)是A的分布函数，样本的分布函数如下：

(1)

在Bayes估计中，θ是取值于参数空间Θ的一个随机变量，分布函数式(1)实际就是随机变量θ为某一特定值条件下的样本的分布情况，因此，式(1)可被改写为：

(2)

(3)

g(a1，a2…an，θ)=g(a1，a2，…，an|θ)h(θ)

(4)

(5)

(6)

称之为θ的Bayes估计。

令右式为0，交换积分次序，并利用式(4)得：

(7)

令:

(8)

其中，

(9)

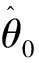
2 Bayes方法在现场点荷载强度中的应用

(10)

式中，i=1,2，…，n，式(10)即是式(9)在离散状态下的Bayes公式。式(10)中{p(A1)，p(A2),…,p(An)}称为验前分布，B为发生的事件；P(Ai|B),i=1,2,…,n为验后分布，综合了前信息和试验所提供的信息[9]。

由于对岩石强度的试验价格昂贵，时间周期长，且取样比较困难，人们总是希望通过少量的实验来获得准确而大量的信息。特别是现场点荷载强度的测试，其取样源于现场随机取样，并且试样的形状和尺寸也是带某一范围内随机的。现场点荷载强度测试本身就是一个随机性的测试，因此对现场少量的试验数据进行Bayes判断显为重要，特别是随着Bayes方法在岩土工工程中的应用越来越广泛。现以现场点荷载强度为例，现场点荷载强度为一随机变量，用X表示，X1，X2，…,Xn为X的样本，这种随机变量X样本可视为正态分布，即X～N(μσ2)，设小样本计算出的均值和方差分别为ν和τ2，则可求出在二次损失函数下μ,σ2的Bayes估计：

(11)

(12)

3 工程实例

以现场点荷载测试为基础，通过少量的现场点荷载强度测试来验证Bayes法在点荷载强度方面的适用性。点荷载强度测试采用SD-1数码点荷载仪。点荷载试样通过现场拾得，取样要求长宽不超过10 cm，由于现场条件的限制，选择能满足仪器的岩样都可以。这次所选择的岩样长宽主要在小于15 cm的块状岩块，加荷间距以30～50 mm为宜，考虑到现场的条件限制，试样的加荷间距为40～60 mm的岩块，岩块试样如图1所示。39组现场点荷载强度测试数据(见表1)。现场点荷载测试试件本身就是随机性的测试。因此，样本完全服从正态分布。样本均值μ=3.29，σ2=4.49。即先验分布服从N(3.29，4.49)。

图1 岩块试样

在表1中随机取5个数据组成一组，并且随机取4组，如表2所示。计算出的均值方差也如表2所示。通过Bayes方法估计即式(11)和式(12)计算所获得的均值和方差如表2所示。计算值和样本误差值计算见表3，由表3可知误差基本都小于10%，说明后验分布的均值和方差与总体样本的均值和方案值比较接近，因此Bayes方法适合用于现场点荷载强度的估计。

为了进一步说明上述小样本Bayes统计方法的适用性，再随机取4组数据，每组7个，对Bayes统计方法的适用性进行验证，如表4所示。

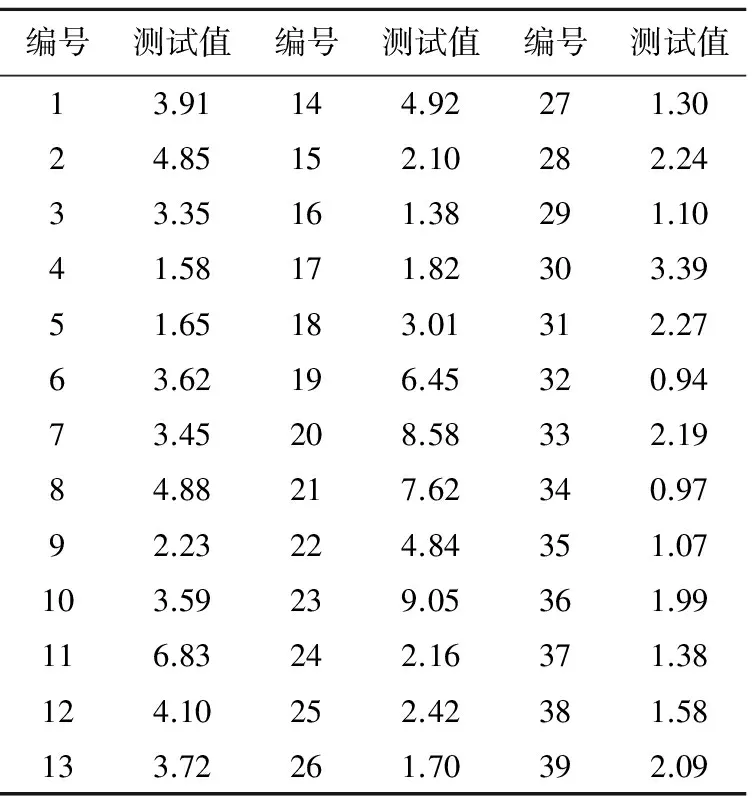
表1 现场点荷载强度测试结果

表2 随机抽取计算均值和计算方差

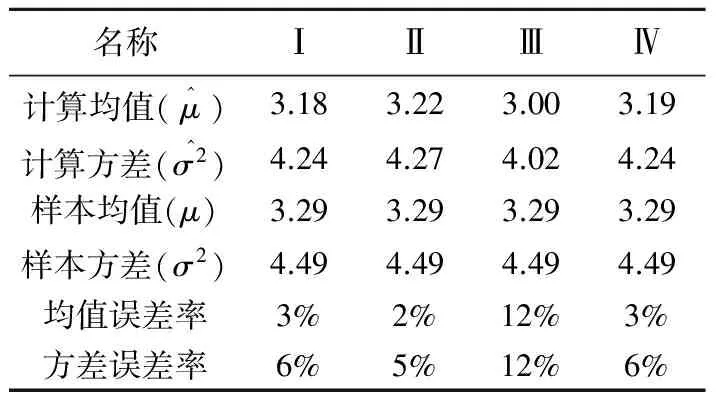
表3 计算值和样本值误差计算结果

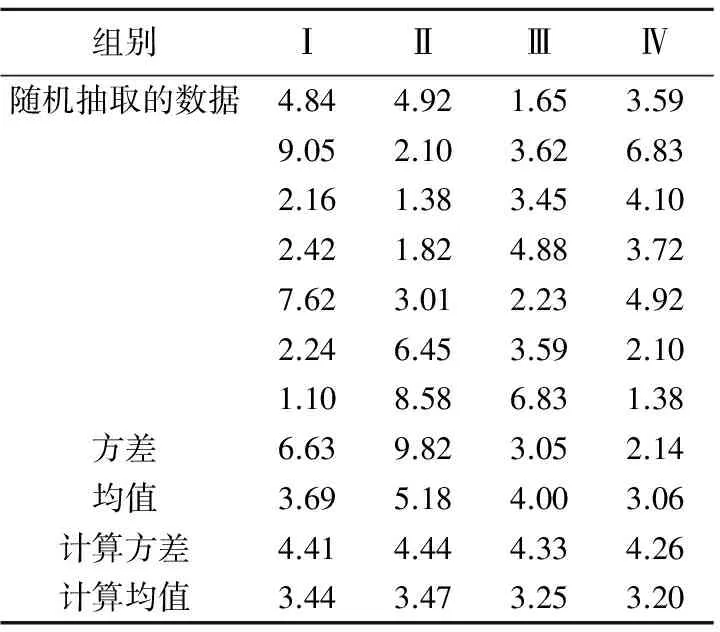
表4 随机抽取计算均值和计算方差

计算出的均值方差也如表4所示。通过Bayes方法估计即式(11)和式(12)计算所获得的均值和方差由表4所示。表5所示的计算值与样本值误差全部都小于10%，如表5所示，说明后验分布的均值和方差与总体样本的均值和方案值比较接近，因此Bayes方法适合用于现场点荷载强度的估计。

因此，在矿山需要获得岩体或岩石的强度参数时，可以利用本方法通过少量的试验数据来获得比较准确的岩石或岩体力学参数。

表5 计算值和样本值误差计算结果

4 结 论

本文根据现场点荷载强度测试的特殊性，即试样尺寸、形状都不规则，并且试样的采集都是现场随机拾取。针对这些特点，从Bayes原理出发，针对现场点荷载强度测试的已有的少量样本信息，通过随机取样计算出现场点荷载强度后验分布统计量的计算公式，分析了Bayes统计方法在现场点荷载强度测试领域方面的应用。并对其可靠性和计算误差做了详细的统计，统计结果表明，利用Bayes方法对现场点荷载强度进行概率分布参数的计算，能够通过小样本数据，获得岩石现场点荷载强度的概率分布，具有较高的实用价值。但是值得注意的是，该方法必须建立在数据搜集形成的大样本基础上，否则结果没有实际意义[4]。

参考文献：

[1]严春风,陈洪凯,张建辉.岩石力学参数的概率分布的Bayes推断[J].重庆建筑大学学报,1997,19(2):65-71.

[2]毕忠伟,丁德馨,饶 龙,等.岩石参数Bayes估计中验前样本可信度的研究[J].水利学报,2006,37(8):1000-1003.

[3]邓 建,李夕兵,古德生.岩石力学参数概率分布的信息熵推断[J].岩石力学与工程学报,2004,23(13):2178-2181.

[4]闫春岭.岩石抗压强度的Bayes推断[J].山东科技大学学报(自然科学版)，2012,31(4).

[5]光耀华.岩石抗剪强度指标的概率分析[J].岩石力学与工程学报,1994,13(4):349-356.

[6]蒋树屏.扩张卡尔曼滤波器有限元法耦合算法及其隧道工程应用[J].岩土工程学报,1996,18(4):11-19.

[7]徐 军，雷 用，郑颖人.岩土参数概率分布推断的模糊Bayes方法探讨[J].岩土力学,2000,29(4):88-91.

[8]杨 坤.模糊方法在煤矿区矸石山可靠性分析中的应用[J].山东科技大学学报(自然科学版),2010,29(4):88-91.

[9]毕忠伟.岩体力学参数推断的Bayes方法及截尾可靠度的研究与应用[D].长沙：中南大学，2008.