非圆齿轮设计及其运动学分析

张 健，饶 鹏，郑 彬，张敬东，起雪梅

(攀枝花学院 交通与汽车工程学院，四川 攀枝花 617000)

0 引 言

非圆齿轮结合了凸轮与圆齿轮的优点，已经广泛运用于农业、轻工、冶金等各个领域[1-3]。在传统的非圆齿轮设计中，运用VB对Solidwork软件第二次开发，模拟非圆齿轮齿廓的行成过程，通过实体布尔运算得出非圆齿轮的实体模型[4-5]。该建模方法虽然精确，但是软件的二次开发难度大、对物力财力及人力要求太高，在实际应用中经济性差[6]。非圆齿轮机构在运动学方面的特征就是能实现主动件和从动件转角间的非线性关系。为了验证这种非线性关系，已有学者利用CAD软件造型后导入ADAMS进行运动学仿真[7-8]。但无法规避模型在导入过程中存在模型信息损失问题[9-10]，从而影响分析的准确性。

分别利用椭圆齿轮的几何学知识和刀具与齿廓啮合轨迹，推导出各阶非圆齿轮节曲线和齿廓的一般方程,并结合MATLAB参数化设计和Pro/E实体化特征操作混合建模及Pro/Mechanism design模块进行运动学仿真。可有效提高非圆齿轮的设计效率和解决运动学分析准确性问题。

1 非圆齿轮设计

1.1 非圆齿轮节曲线方程

非圆齿轮的运动特性取决于节曲线，要描述其运动特性，须推导非圆齿轮的节曲线方程。以非圆齿轮的典例—椭圆齿轮为基础，推导出高阶齿轮的节曲线方程，1阶椭圆几何关系如图1所示。

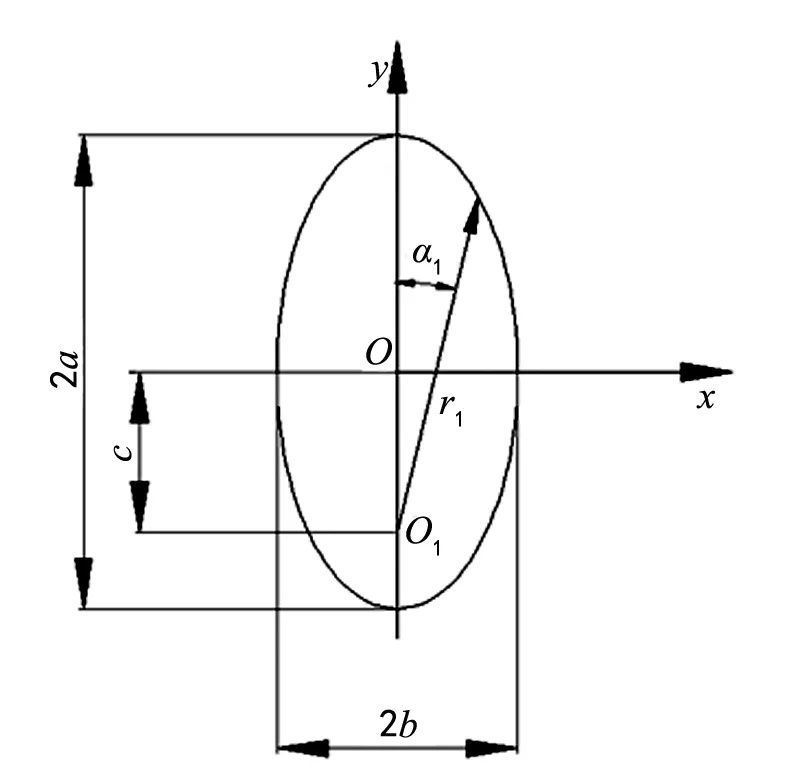
图1 椭圆几何关系

如果将极坐标的原点放置在椭圆的一个焦点上，该点也是齿轮1(主动轮)的回转中心，则它的极坐标为：

(1)

p1=a(1-e12)

(2)

式(1)和式(2)中e1为椭圆(齿轮1)的偏心率，根据其性质：

(3)

齿轮1的向径r1的变化周期为2π，即n1=1。齿轮2(从动齿轮)的向径r2回转一周时，变化周期数为n2，将式(1)带入节曲线封闭条件式:

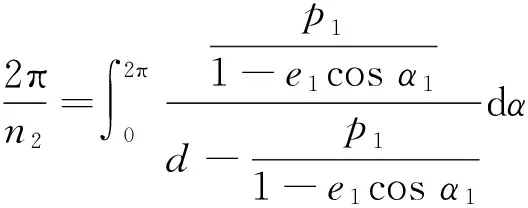
(4)

由此，解得中心距：

(5)

在齿轮啮合中有：

(6)

将式(1)带入式(6)得：

(7)

(8)

r2的变化周期为：

(9)

齿轮1和齿轮2的传动比：

(10)

若将式(1)的极角缩小整数倍n1(n1>1)，保持向径r1不变，则其方程可以写为：

(11)

同理，齿轮2的极坐标可以写为：

(12)

传动比：

i=

(13)

中心距：

(14)

故式(11)和式(12)是非圆齿轮副啮合时的节曲线的方程。

1.2 节曲线绘制

由节曲线方程可以看出，控制非圆齿轮副传动比和齿廓形状的参数是齿轮的离心率e1和两齿轮的阶数n1、n2，所以非圆齿轮副的传动组合形式是非常多的。为了避免内容冗杂及保证节曲线设计合理性，举以下实例进行分析。

取椭圆长半轴a=20 mm，主动轮离心率e1=0.3，阶数n1=1；从动轮阶数n2=1、2、3、4得到不同的从动齿轮副啮合节曲线如图2(a)。同样，取椭圆长半轴a=20 mm，主动轮离心率e1=0.5，阶数n1=3，从动轮阶数n2=3、4、5得到不同的从动齿轮副啮合节曲线如图2(b)。 对比综合图2(a)和图2(b)可得出，非圆齿轮离心率和阶数越大，内凹越明显，总体外形尺寸越大，变传动比周期循环越小；离心率和阶数越小，外凸越明显，外形尺寸越小，变传动比周期循环越大。

图2 不同阶数及离心率

1.3 齿廓设计及三维模型建立

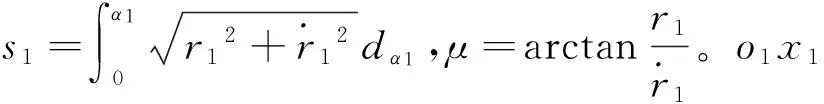
则在坐标系pxdyd中，o1点的坐标为:

(15)

坐标系o1x1y1和pxdyd的相互变换为:

(16)

现规定，正向面对齿廓，位于左侧的齿廓为左齿廓，反之为右齿廓。对第K号齿廓有:

s=s1-(k-1)pn=s1-(k-1)πm

(17)

式中：m为齿轮模数。

在坐标系pxdyd中，左齿廓啮合点Ekz的坐标为:

(18)

在坐标系pxdyd中，右齿廓啮合点Eky的坐标为:

(19)

运用推导的节曲线及齿廓方程进行MATLAB编程，可计算绘制出椭圆轮齿齿廓，然后导入Pro/E进行三维实体化操作即可得到非圆齿轮模型。

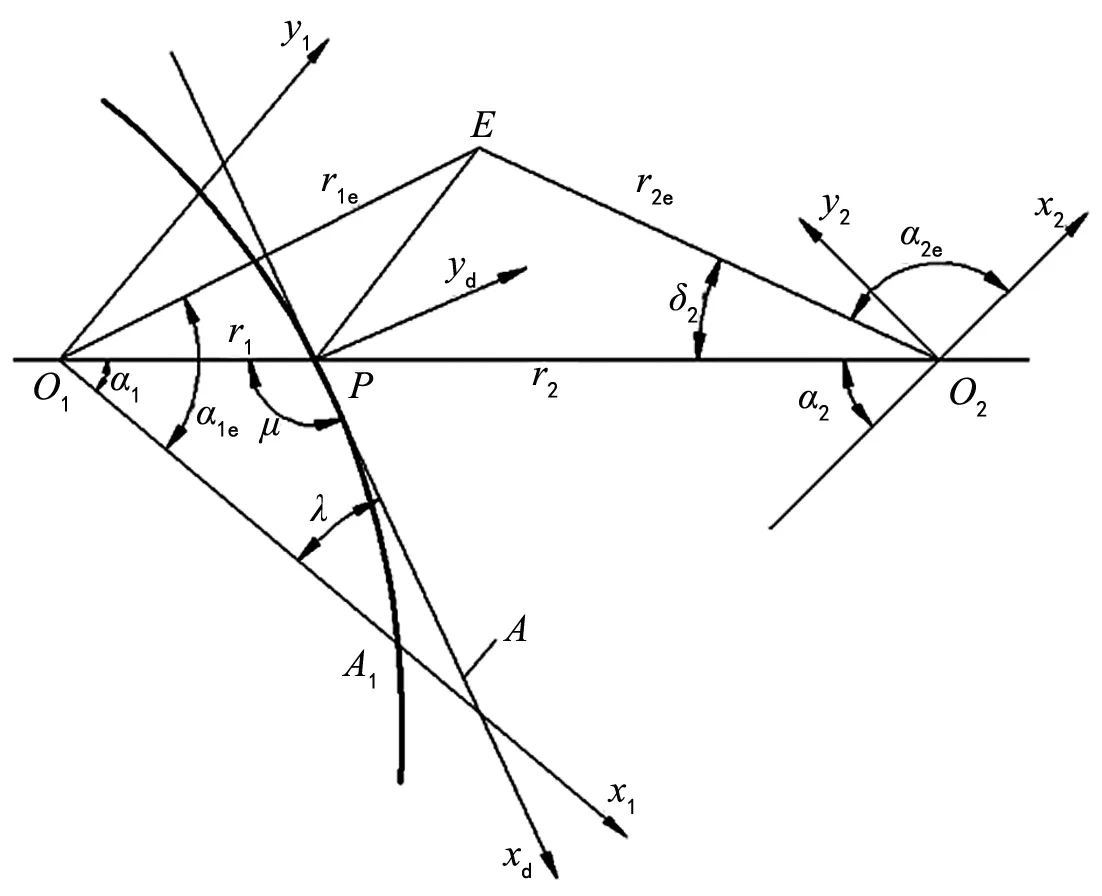
图3 非圆齿轮齿廓生成

2 运动学分析

运动学主要研究点和刚体的运动规律。刚体运动学研究刚体本身的转动过程、角速度、角加速度等更复杂些的运动特征。非圆齿轮则可看着刚体一类进行运动学分析。

2.1 不同阶数和离心率的齿轮副的传动比参数对比分析

取离心率e1=0.3，阶数n1=1，n2=1、2、3、4、5和阶数n1=1、2、3、4、5，n2=1得到齿轮副对应的理论传动比如图4所示。

从图4中可以看出，在非圆齿轮副主动齿轮离心率e1=0.3固定不变的情况下，齿轮阶数由1～5，传动比曲线的波峰和波谷逐渐增大且差值越大；主动齿轮阶数n1=1固定不变时，传动比周期为2 π；从动齿轮阶数n2=1固定不变时，主动齿轮阶数由1到5，传动比周期从2 π到小于0.5 π。所以高阶非圆齿轮的传动比受其阶数控制。

取离心率e1=0.3、0.5、0.7、0.9，阶数n1=n2=2，得到理论的传动比关系如图5所示。

从图5中可以看出，非圆齿轮副阶数n1=n2=2为定值时，离心率e1由0.3增加到0.9时，传动比的周期由4 π减小到2.25 π；传动比曲线的波峰值由2增加到19，波谷逐渐减小，变化幅值(起伏)越大。所以非圆齿轮传动比同样受其离心率的控制。

图4 不同阶数和离心率齿轮副的理论传动比

图5 理论传动比与不同离心率

2.2 角速度、角加速度与时间的关系

取e1=0.3，n1=1、2、3，n2=1进行分析，得到角速度、角加速度与时间的理论关系曲线如图6所示。

图6 角速度、角加速度与时间的理论关系

3 运动学仿真分析

现以较典型的2阶椭圆齿轮副为例，按之前所述方法取表1中数据进行建模。在Pro/E中，按照【销钉装配】、【面对齐】装配方式完成齿轮副的装配，得到2阶两共轭非圆齿轮的仿真啮合装配图如图7所示。

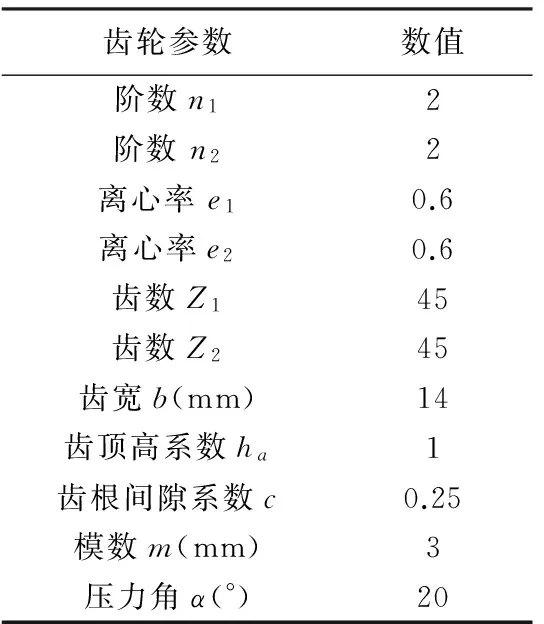
表1 椭圆齿轮基本参数

图7 齿轮的仿真啮合装配图

接着在Mechanism design模块中为模型添加【凸轮】，转速为20 rad/s，持续时间为40 s的伺服电动机。然后经过回放并保存分析结果，再选取齿轮副旋转轴为测量对象，最后【绘制选定结果集所选测量的图形】，得到齿轮副的角速度及角加速度仿真曲线，如图8所示。该齿轮副的角速度及角加速度理论曲线如图9所示。

图8 齿轮副的角速度及角加速度仿真曲线

由图8分析可知，从动齿轮的旋转周期为9 s，角速度曲线在波谷和加速度曲线在上升及下降过程中出现突变，这是由于椭圆齿轮副的非匀变速传动特性所引的起不可避免的震动、冲击。对比齿轮副的仿真角速度及角加速度曲线(见图8)与理论角速度及角加速度曲线(见图9)，可以发现所对应的曲线在同一时间段变化趋势基本相同。

4 结 论

(1) 从动齿轮阶数一定，主动齿轮阶数越大，传动比、角位移、角速度周期越小，角加速度的幅值越大。

(2) 离心率越大，传动比变化幅值(起伏)越大，传动比变化周期越小。

(3) 经过对比分析，从动齿轮运动仿真规律基本符合理论角速度、角加速度函数关系，证明设计正确且方法切实可行。

参考文献：

[1] 叶秉良,易卫明,俞高红,等.不完全非圆齿轮传动钵苗移栽机构缓冲装置研究[J].农业机械学报,2017(3):69-75.

[2] 胡紫阳,杨 辉,李大柱,等.平流泵用非圆齿轮副的优化设计及实验分析[J].中国机械工程,2016(22):3082-3087.

[3] 韩 江,高 婷,江本赤,等.非圆齿轮齿廓特性分析及偏差测量方法研究[J].电子测量与仪器学报,2016(10):1520-1533.

[4] 焉兆超,管殿柱,陈 洋,等.基于SolidWorks的高阶椭圆齿轮副节曲线设计系统[J].机械传动,2017(1):169-172.

[5] 钱孟波,俞高红,俞益波,等.基于VB和ADAMS的水稻钵苗栽植机构参数优化及试验分析[J].江苏大学学报(自然科学版),2015(5):539-544.

[6] 李书平,侯振林.基于UG二次开发的齿轮参数化精确建模方法研究[J].机械设计与制造,2011(9):190-192.

[7] 赵 宁,孙向轩,蔺彦虎,等.直齿圆柱齿轮差速器运动学与动力学分析仿真[J].计算机仿真,2012(8):344- 348.

[8] 刘永平,杨 存,孙 旋.基于ADAMS的非圆齿轮运动学仿真分析[J].机械传动,2014(6):106-109.

[9] 张 朋,欧阳林子.Pro/E、ADAMS和ANSYS之间数据交换方法[J].机床与液压,2010(6):110-112.

[10] 张 健,陈 琳,张 祺,等. “S”形齿轮参数化设计及有限元分析[J].组合机床与自动化加工技术,2015(3):44-47.

[11] 俞高红,虞佳萍,童俊华,等.一种共轭凹凸型非圆齿轮机构的设计[J].中国机械工程,2016(16):2155-215+2165.