利用高次差与自相关函数对周跳探测与处理

陈石平，郑健超，谈书才

（1 广州奥格智能科技有限公司，广州 510663；2 湖南交通工程学院，湖南衡阳 421219）

0 引言

在高精度BD/GPS数据处理中，由于接收机所获得的载波相位是用于估计参数的主要观测量。在连续观测中由于某种原因（卫星信号被遮挡而无法到达接收机，外界干扰或者是环境恶劣引起接收机失锁）而导致整周计数发生错误，使相位观测值比正常值差数个整数周的跳跃，不足一周的部分仍然工作，该跳跃称为周跳[1]。周跳也是载波相位观测值经常遇到的问题，因而周跳的探测与处理，就成为载波相位测量数据预处理中一项常规的工作。周跳的发生往往存在连续性，产生周跳使得定位精度变低，因此有必要对多历元发生周跳的情况进行研究与分析。基于观测值变化规律周跳的处理法有[2]：屏幕扫描法，多项式拟合法，高次差法等。

1 基本原理

1.1 高次差原理

定义：对于一个给定的数列{xn}，把它的前后两项xn+1与xn的差xn+1-xn记为Δxn，得到一个新的数列{Δxn}，数列Δxn称为原数列{xn}的1次差数列，如果 Δ2xn=Δxn+1-Δxn，则数列{Δ2xn}是{xn}的 2 次差数列，依此类推可得出数列{xn}的r次差数列{Δrxn}，其中n，r为正整数。如果某数列的r次差是一非零常数列，文献3则称此数列为r次等差数列，显然r次等差数列是r次差数列的特例。二差次或二差次以上数列统称为高次差数列。高次差是对时间序列进行多次差分，观测的数据被放大，其计算只涉及加减法，计算复杂度低，且具有抗粗差的能力，在数据粗差的剔除应用中，都取得了良好效果。

在载波相位 RTK高精度定位中，在载波相位观测期间，由于其它物体等的遮挡、电离层电子的剧烈运动、卫星仰角低、存在多路径效应以及接收机本身震荡的不稳定或软件故障等原因，会导致信号失锁，并可能引起整周计数跳变，产生周跳，周跳的探测与处理必须在载波相位模糊度固定前进行，是精密定位相位观测处理的一项重要内容。1985年Remondi在文献4首次提出用差分法进行周跳探测与处理，对相位原始观测序列历元间高次差，如果没有周跳，其高次差表现为偶然误差特性，围绕“0”附近变化的随机序列(不考虑误差影响)；文献5提出如果周跳发生，则会破坏这种规律性，在周跳历元高次差发生突变且邻近历元数值上满足一定的比例关系，确定周跳发生的位置和大小，完成探测较大的周跳与处理。

文献5提出周跳探测的基本思路:以输出的周数为基础，通过计算不同历元间的周数高次差，组成一个关于时间的特征序列，通过判断特征序列尽可能地消除与时间有关的序列。如果没有发生周跳，特征序列随时间的变化应是平稳的；如果发生周跳这个平滑的序列就发生剧烈的跳变，探测检测量的变化是否符合评定指标，进而确定周跳发生的位置和大小。

对于高精度BD/GPS接收机测量载波相位观测值φ等信息，输出频率一般为1Hz，因此以1s为间隔进行采集数据，得到相位观测值序列φn（n为自然数），1次差数列为Δ1φn =φn+1-φn，2次差周数数列为Δ2φn =Δ1φn+1-Δ1φn，r次差周数数列为Δr φn =Δr-1φn+1-Δr-1φn。

一般来说若不发生周跳也存在 1次差 Δ1φn≠0，2次差Δ2φn≠0，近似于0或者围绕0上下波动，一般需要求出3次、4次（甚至更高的）次差。

文献6提出在4次差周数运算过程中，若不考虑Φn之间的计算（如不发生周跳），只考虑其周跳周数，那么1个周跳的4次差周数的特征序列如表1所示，其比值分别为1、1:-1、1:-2:1、1:-3:3:-1，特征序列具有偶函数性质。此外由概率可知，周跳次数越多其出现的概率越小，连续4次以上的周跳其概率非常小。

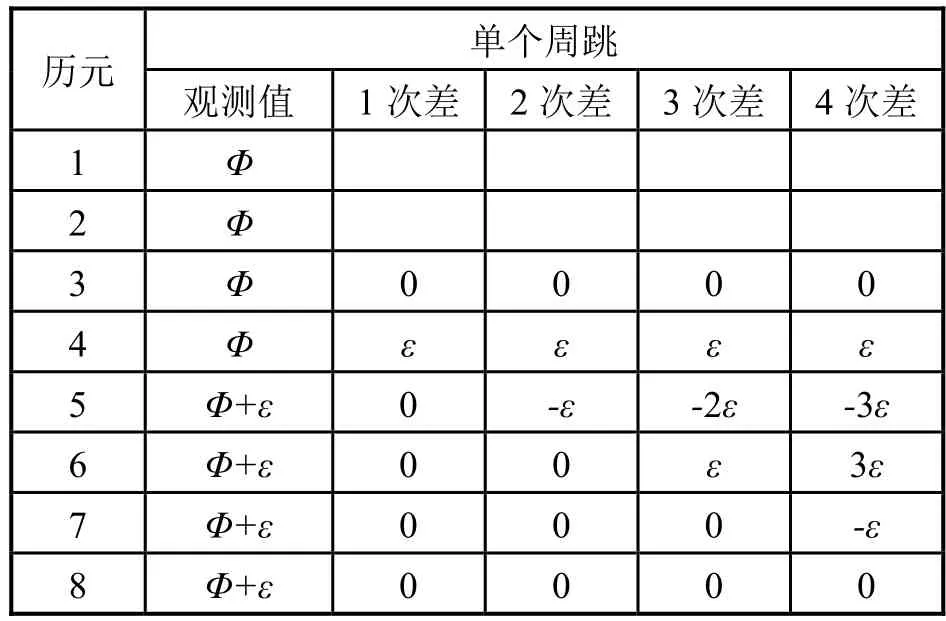
表1 单个周跳4次差周数特征序列

若不发生周跳，周数递增恒定，有Φn-Φn-1=0，理论上1次差Δ1Φn=Φn-Φn-1=0，表1中若在i历元产生了单个周跳ε，周数为Φi=Φi-1+ε，则 1次差Δ1Φi-1=Φi-Φi-1=ε，1次差中产生 1个阶跃，其余 1次差数列为零。2 次差周数：Δ2Φi-1=Δ1Φi-Δ1Φi-1=ε，Δ2Φi=Δ1Φi+1-Δ1Φi=-ε，2 次差中产生 2 个阶跃（1 正1负，和为0），其余2次差数列为零。3次差周数：Δ3Φi-2=Δ2Φi-1-Δ2Φi-2=ε，Δ3Φi-1=Δ2Φi-Δ2Φi-1=-2ε，Δ3Φi=Δ2Φi+1-Δ2Φi=ε，3次差中产生 3个阶跃（2正 1负，和为0），其余3次差数列为零。4次差周数：Δ4Φi-3=Δ3Φi-2-Δ3Φi-3=ε，Δ4Φi-2=Δ3Φi-1-Δ3Φi-2=-3ε，Δ4Φi-1=Δ3Φi-Δ3Φi-1=3ε，Δ4Φi=Δ3Φi+1-Δ3Φi=-ε，4 次差中产生4个阶跃（2正2负，和为0），其余4次差数列为零。依此类推，r次差产生r个阶跃。

对于不发生周跳其周数递增恒定：当定位周跳发生单个周跳时就产生突变而严重破坏这种规律性，4次差周数可以产生3倍周跳周数3ε，相当于放大作用，若ε=Φ/3，4次差可达Φ，若ε=Φ，4次差可达3Φ，随着周跳周数的增加，4次差变化更加明显。根据这种特性就可以把定位周跳探测出来。使用高次差法来探测与处理这些定位周跳，即对原始观测值在相邻的两个周数观测值间依次求r次差，于是就得到r次差，其中有周跳时刻的观测值会呈现很大的变化。

1.2 自相关系数的原理

随机过程的数字特征常用均值、方差、相关函数进行表征，它们都是从随机变量的数字特征推广而来，数字特征一般不是常数，而是时间t（或n）的函数。均值和方差只描述了随机过程在某个特定时刻的统计特性，所用的只是一维概率密度，并不能反映随机过程在两个不同时刻状态之间的联系，而相关函数是能反映两个不同时刻状态之间相关程度的数字特征。

自相关函数（简称相关函数，且为偶函数）是描述随机信号X(t)在任意两个不同时刻t1，t2的取值之间的相关程度，也可以表征时间序列X(n)在任意两个不同序列n1、n2取值的相关性。相关函数是随机过程联合统计特性中重要的数字特征，它是利用相关性原则的一种检测方法，常被用于测量未知数字信息与已知数字信息的相关程度，检查信号的相关性必须对用归一化处理的自相关系数作有效的研究，即自相关系数函数F，随机序列具有良好的自相关特性，如GPS的C/A码自相关系数的尖峰很尖[7]：主峰F(0)与侧峰F(1)对数比为24dB，自相关函数在主峰左右两边附近都接近于 0，即序列随机性越大，尖峰越尖；而对于相关序列主峰左右两边变化较为缓慢，直至接近 0，即序列相关性越大，尖峰越小。

相关系数F的正负号只表示相关的方向，绝对值表示相关的程度。对于相关系数的大小所表示的意义目前在统计学界尚不一致，但相关的程度通常这样认为：0≤F≤0.3为微相关、0.3＜F≤0.5为实相关、0.5＜F≤0.8为显著相关、0.8＜F≤1为高度相关。

对比周跳和定位周跳，两者存在很多相似之处，如两者产生的后果都会降低定位精度性能，基于此本文提出利用4次差和自相关系数作为载波相位周跳探测与处理的一种算法。

2 基于高次差和自相关系数探测法

基于高次差和自相关系数探测法具体如下：

（1）数据采集：根据高精度 BD/GPS接收机观测载波相位观测值，获取载波相位观测值数据，一般要求n≥20，Φ=（Φ1，Φ2，…Φn-1，Φn）；

（2）对采集的观测值进行r（r≤4）次差运算，分别得到四种数据：Δ1Φn，Δ2Φn，Δ3Φn，Δ4Φn；

（3）以历元为横坐标，周跳 4次差的归一化自相关系数函数数据为纵坐标，计算公式为：

其中，n1，n2为自然数，为自相关函数，为方差函数，为均值函数。

（4）对获取的数据，编写相应的软件代码，实现归一化的自相关系数函数功能；

（5）周跳探测：检查归一化自相关系数曲线图，根据相关的程度进行判断如曲线很平缓图顶部变化缓慢（主峰FΦ(0)与最大侧峰FΦ(1)相差绝对值小于1.5），3、4次差无阶跃，证明原序列是稳定的，观测值是稳定的；如曲线图顶部出现尖峰（主峰FΦ(0)与最大侧峰FΦ(1)相差绝对值大于 1.5），证明原序列是不稳定的，观测值不稳定，出现了周跳，存在奇异点，尖峰越尖，周跳越厉害。

（6）周跳处理：对于被断定是奇异点的周跳数据，可以使用2种处理方法[1]：修复是从发生周跳历元开始的后续历元观测值减去一个固定的数值添加模糊度参数是从周跳发生历元处引入一个新的模糊度参数。

3 试验分析

3.1 无周跳

使用无周跳的实测数据（文献2表1-3），使用上面的处理方式得到的无周跳 1、2、3、4次差归一化自相关系数曲线如图1～图4所示。

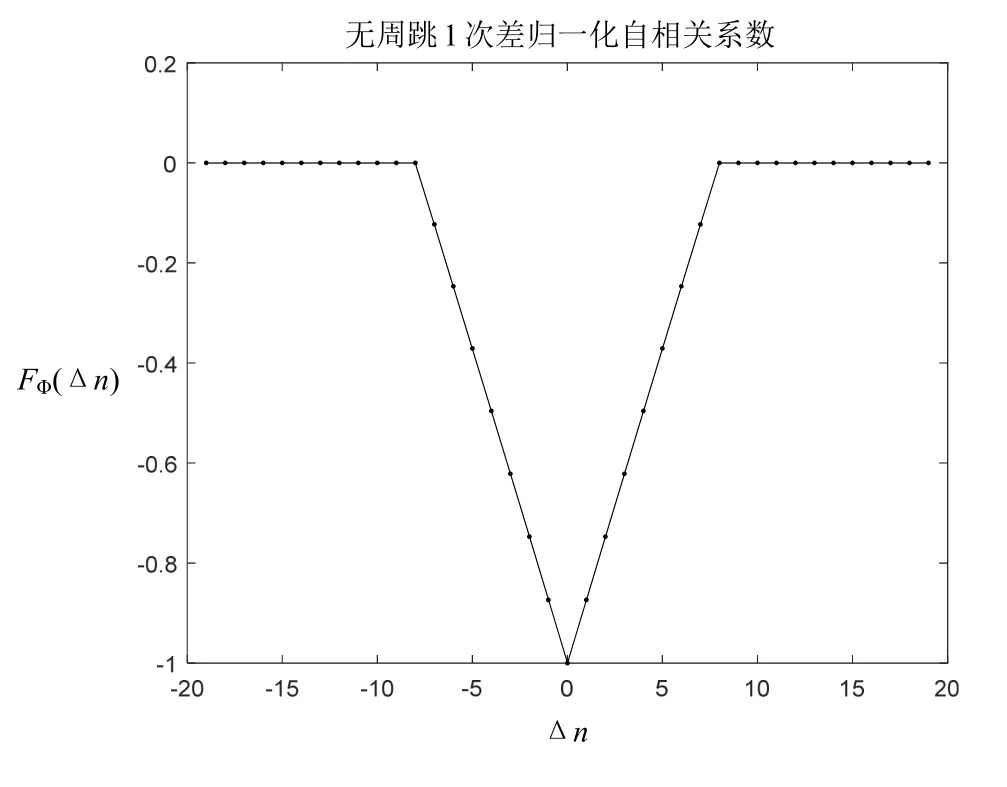
图1 无周跳1次差归一化自相关系数

图2 无周跳2次差归一化自相关系数

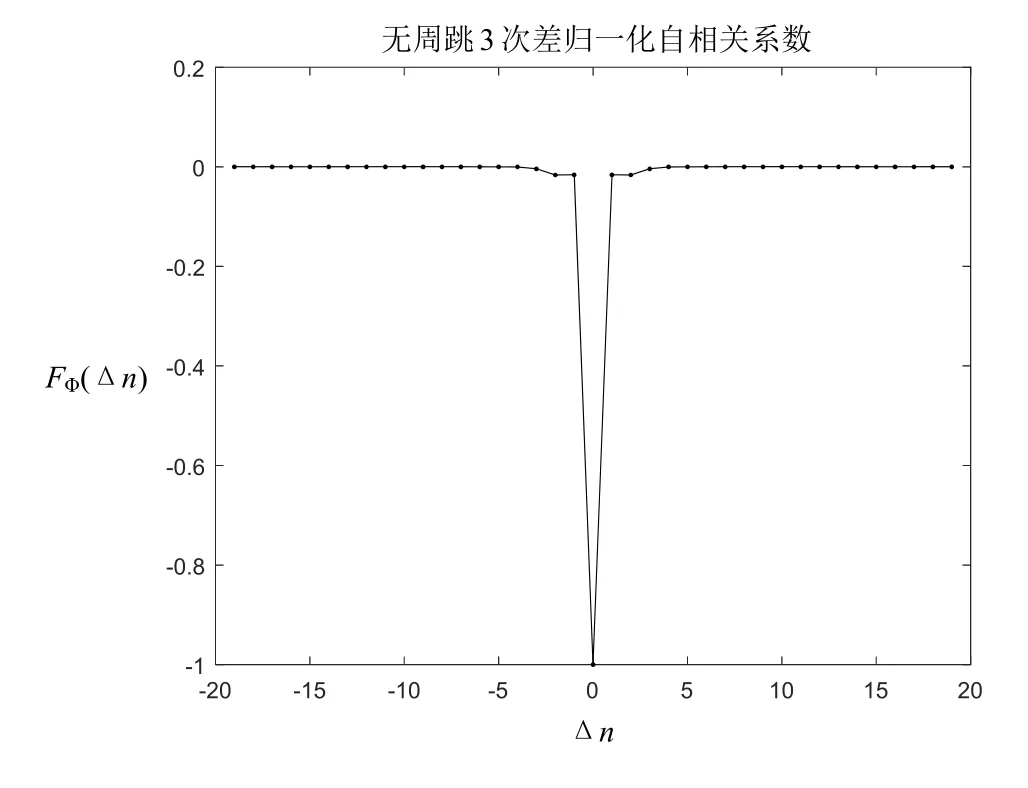
图3 无周跳3次差归一化自相关系数

图1～图3的归一化自相关系数变化很平滑，无阶跃数据，图4产生了几个阶跃，其最大值小于0.5，属于“实相关”，且3、4次差的数据均在“0”上下波动，因此可以认为观测数据无周跳。

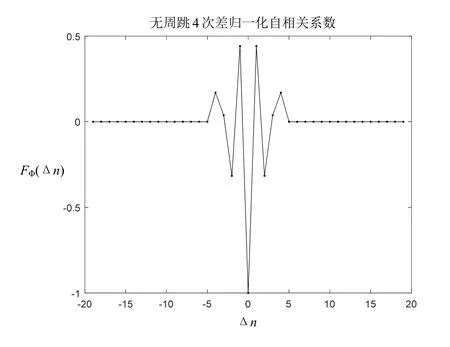
图4 无周跳4次差归一化自相关系数

3.2 单个周跳

使用单个周跳的数据（文献2表1-4），某个历元发生了周跳，载波相位观测值比正确值少了100，使用上面的处理方式得到单个周跳 1、2、3、4次差归一化自相关系数曲线如图5和图6所示，由于 1、2次差归一化自相关系数曲线图变化很平滑，无阶跃数据，与图1、图2差不多，具体参见图1、图2。

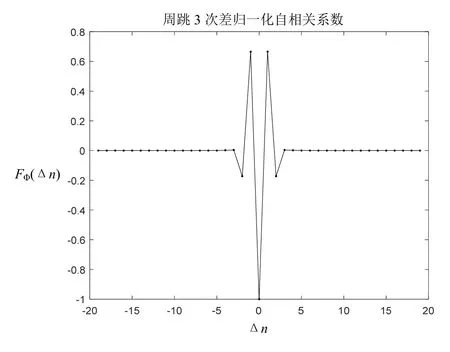
图5 周跳3次差归一化自相关系数

图5、图6均产生了几个阶跃[9][10]，图5、图6的最大值均大于0.6，属于“显著相关”，且3、4次差的数据比值分别约为1: -2:1、1: -3:3: -1，其比值近似于特征序列比值[11]，均远离“0”上下波动，4次差比3次差偏离更大，因此可以认为观测数据存在周跳。

图6 周跳4次差归一化自相关系数

4 结束语

本文针对周跳现象出现的情况，结合高次差和自相关函数特性，提出一种基于高次差和自相关函数判断是否出现周跳，对其算法进行介绍、分析和推导，该算法具有较为深厚的理论基础，并通过试验测试，结果表明：结合周数的高次差和自相关函数有效地探测周跳，并判断出周跳的位置，同时进行修正，进而提高观测值可靠性和准确性，具有较好的效果。

参考文献：

[1]李征航, 张小红.卫星导航定位新技术高精度数据处理方法[M].武汉:武汉大学出版社,2013:27-30.

[2]李征航, 黄劲松, 独知行等.BD/GPS测量[M].武汉:武汉大学出版社, 2013:25-30.

[3]华罗庚.华罗庚科普著作选集[M].上海:上海教育出版社, 1997.

[4]Remondi B W.Performing centimeters relative surveying in seconds using BD/GPS carrier phase [J].1985 Journal of the Institute of Navigation, 1985, 32(4):386-400.

[5]王一强, 严新生, 白征东等.一种探测与处理周跳的组合方法[C].中国全球定位系统技术应用协会第九次年会, 2007

[6]王爱生, 欧吉坤.周跳在高阶差分中的时序特征及精确估计[J].大地测量与地球动力学, 2008,(5):59-64.

[7]谢钢.BD/GPS原则与接收机设计[M].北京: 电子工业出版社, 2014:24-26

[8]金国雄.BD/GPS卫星定位的应用与数据处理[M].上海:同济大学出版社, 2003:207-215.

[9]陈石平, 张乾, 何睿.基于互相关函数的降低北斗定位漂移算法研究[C].第七届中国卫星导航学术年会论文集--S01北斗/GNSS应用技术,2016.

[10]陈石平, 廖丁毅, 何睿.基于自相关函数的降低北斗定位漂移算法研究[C].第七届中国卫星导航学术年会论文集--S01北斗/GNSS应用技术,2017.

[11]姚全德.独立周跳和非独立周跳在高次差法中的分析[J].地理空间信息,2012 (3):88-90.