双观测站水下纯方位多目标跟踪的数据关联算法
苏 骏, 李亚安, 陈 晓, 赵振轶
双观测站水下纯方位多目标跟踪的数据关联算法
苏 骏, 李亚安, 陈 晓, 赵振轶
(西北工业大学 航海学院, 陕西 西安, 710072)
针对双观测站纯方位系统在定位多个目标时, 产生的大量虚假定位点使得量测数据依据目标数量和虚假量测数量都呈平方倍数增长的问题, 文中在最近邻域法(NNF)的基础上增加了一组事件, 考虑了跟踪门内不存在有效量测的情况, 改进得出修正最近邻域法(MNNF); 简化了联合概率数据互联算法(JPDA)的计算步骤, 对公共区域中的量测统一做弱加权, 提出了修正概率数据关联算法(MPDA), 并对以上方法做了仿真及比较。结果表明, 利用该2种方法在双观测站纯方位系统存在“鬼点”的情况下有较为理想的估计结果, 并且MPDA算法的效果明显优于MNNF算法, 可有效跟踪目标。
水下多目标跟踪; 纯方位; 数据关联; 双观测站
0 引言
纯方位多目标跟踪[1-6]属于无源多目标跟踪, 是多目标跟踪领域的一个分支。它的优点在于, 观测者可以在隐蔽的状态下, 实时的对目标进行观测, 从而可以掌握主动权。因此, 水下纯方位多目标跟踪的研究和发展, 对于海洋领土防御、区域的协同防御、海上安全作业以及海洋资源的保护与开发具有重要的战略意义。
Singer等[7-9]率先研究出最近邻域法(nearest neighbor filter, NNF), 该算法非常简洁, 只需计算出每一时刻目标所有量测值的信息加权范数并做比较, 选择新息范数最小的那个量测值作为真实值滤波即可, 但也因此容易跟丢或误跟目标。之后, Bar-Shalom等[10-12]和吴佳芯[13]提出了概率数据互联(probabilistic data association, PDA) 算法并进行了推广, 使得滤波器可同时对多个目标实时分析。同时有学者提出了聚合矩阵的概念, 考虑了跟踪门内所有量测间的关系, 研究出联合概率数据互联[14-18](joint probabilistic data association, JPDA)算法, 该算法相比之前的算法精度更高, 考虑的因素最全, 但公式计算也较为繁琐, 仿真运行时间较久, 实时性相对较差, 在实际环境中, 可能无法在有效时间内跟踪目标。
基于纯方位双观测站对水下多目标进行跟踪, 比单观测站具有更佳的可观测性能, 但也会产生大量虚假定位点。这些虚假定位点会使量测数据依据目标数量和虚假量测数量呈平方倍数增长, 因此传统的数据关联方法无法直接运用在此环境中。文中依据NNF法, 重新考虑了跟踪门内无候选量测的情况, 减少算法误跟目标的可能性, 改进得出修正最近邻域法(modified NNF, MNNF);在JPDA的基础上, 精简方法步骤, 并对公共区域中的量测统一做弱加权, 减少误跟概率并降低计算量, 提出了修正概率数据互联算法(modified probabilistic data association, MPDA)。最后对2种方法进行仿真对比。结果表明, 在双站纯方位系统存在“鬼点”的情况下, MPDA 算法的效果明显优于MNNF。即使在方位角的量测误差达到3º时, MPDA 对于2个目标在临近平行运动和小夹角交叉运动条件下, 依然有着不错的分辨效果。
1 适用于纯方位目标跟踪的滤波算法
在实际的水下目标跟踪系统中,目标的状态和量测方程可能存在非线性的情况。面对这种情况, 可以通过对状态和量测方程泰勒展开,并取1阶项来进行线性化并计算估计值[10], 这种滤波方法又称为扩展卡尔曼滤波器(extended Kalman filter, EKF)。
对于非线性离散系统而言, 其目标运动方程和量测方程可描述为


1) 时间更新方程

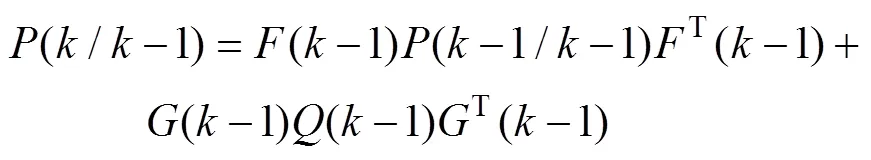
2) 量测更新方程
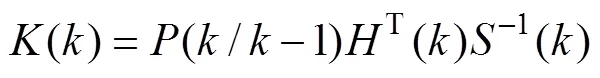




2 适用于水下纯方位系统的数据关联方法
数据关联是水下多目标跟踪技术中最核心、最重要的部分, 其主要过程是将量测的候选值与已知目标的轨迹进行比对, 并确定可能的航迹与有效回波进行配对。而在水下复杂的环境下, 一个目标每一时刻跟踪门内中的观测值可能存在多个, 这些观测值来源于既可能是目标, 也可能是虚假量测。
2.1 纯方位双站系统中的“鬼点”

除了真实量测外还会有虚假量测, 此时产生的虚假定位点又会增加许多。事实上, 这些虚假方位量测每多一个, 就等同于数据关联需要分辨的目标就多了一个, 由此产生的交叉定位点会非常多。因而需要找出一个简便快捷的关联方法以减少计算量。
2.2 修正最近邻域法(MNNF)
最近邻域法的原理是通过选取有效量测中新息加权范数最小的那个量测作为滤波中正确的量测。而事实上, 并不是每一时刻跟踪门内都一定存在候选量测, 这时就需要重新考虑跟踪门内无候选量测的情况。
定义2个事件:

此时的协方差则变为

当量测维数是2时, 参数
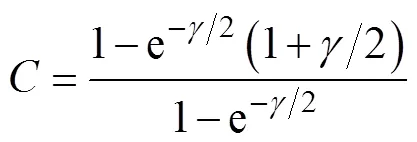
其他步骤与EKF过程一致。
2) 若事件成立, 则按照一般的最近邻域法求解, 即在已筛选过的有效量测集合中, 选取新息加权范数最小的那个作为正确量测。图2为整个MNNF算法流程框图。
MNNF相比NNF考虑了跟踪门内不存在有效量测的情况, 对于模型的建立更加准确, 同时具有非常快的计算速度, 可用于候选量测较多的双站纯方位多目标跟踪系统。然而, 与NNF相同, 对于虚假量测多的情况下, MNNF也存在容易误跟或丢失目标的情况。
2.3 修正概率数据互联算法(MPDA)

1) 计算全部事件的后验概率
同样的, 定义1组事件


根据条件概率公式可得



则参数模型下最终的互联概率
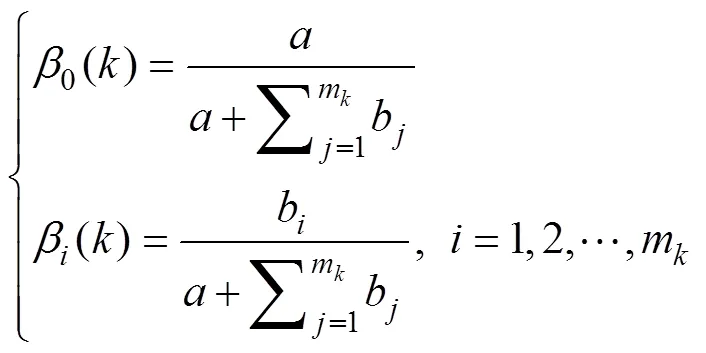
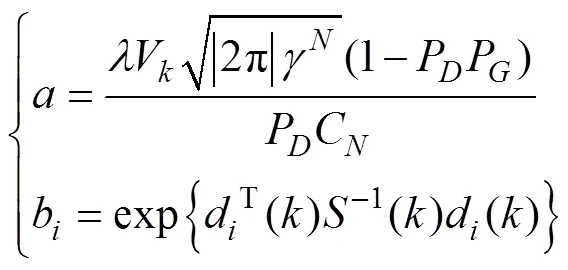
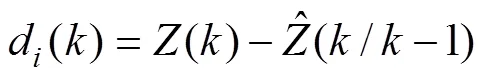

2) 找出所有跟踪门重叠区域中的量测
定义1个同一时刻的公共合集

定义1个时刻1个目标所有非公共区域量测的合集
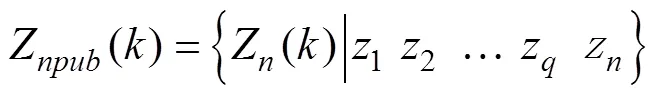
3) 对公共区域中的量测统一做弱加权
对加权因子做归一化处理


4) 计算加权后的互联概率并归一化

则加权后
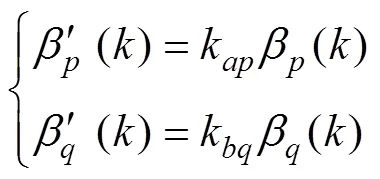
对加权后的互联概率做归一化处理如下。
量测在公共区域时

量测在其他区域时

式(26)和式(27)即为MPDA算法的互联概率计算方法。图3为整个MPDA算法流程框图。
3 目标运动模型与观测方程
3.1 运动模型

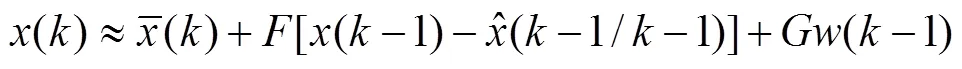
此时的目标状态转移矩阵和噪声转移矩阵为

3.2 观测方程
由双观测站量测所得的量测方位角


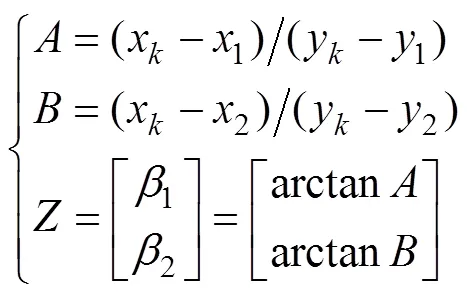
利用上式对目标状态参数求其1阶偏导, 可得量测方程对偏导的雅可比矩

4 仿真结果与分析
文中对水下双站纯方位多目标跟踪下的数据关联方法进行仿真, 并比较MNNF和MPDA在两目标进行小夹角交叉运动时各种误差条件下的跟踪效果。
4.1 试验1
由图5可以看出, 在方位角量测误差均是1º的情况下, MNNF和MPDA均可对目标正确的跟踪, 且基本不存在丢失或者误跟目标的情况, 这是因为1º的测量误差相对而言比较精确, 滤波的结果也会比较好。比较图6可知, MPDA比MNNF的均方误差整体上要小一些。

表1 目标初始状态值
试验2: 仅将量测误差从1º增加至3º, 其余条件同试验1, 仿真结果见图7和图8。
由图7可看出, 在方位角量测误差均是3º的情况下, MPDA可对目标进行正确的跟踪, 相对于量测误差为1º时, 只是均方误差有所增加, 但基本不存在误跟目标的情况。由图8可知, MNNF对于目标1的跟踪出现了误跟, 此时MPDA已经优于MNNF很多。
由表2可看出, 量测角误差对于纯方位数据关联算法的跟踪性能影响非常大。

表2 2种算法在不同误差下性能对比
MPDA算法的整体关联正确率远远优于MNNF算法。MPDA算法在量测角误差角达到3º时关联正确率仍可达90%以上, 而超过3º以后其跟踪性能就大幅下降, 4º时其关联准确率已不理想; 而MNNF算法只有在量测角误差为1º左右时关联性能较为不错, 当误差超过2º时其关联性能骤降至78.3%, 而到了3º有一半概率都不能跟踪到正确目标。这是因为纯方位系统属于无源跟踪系统, 其量测值只有方位角信息, 若测量的角度偏差变大会直接影响算法的性能。MPDA方法考虑到了各个量测与目标的关联概率, 尽可能的减少误跟的可能性, 但依然受限于量测角的误差大小。而MNNF法本质上选取离上一个预测值最近的量测作为估计值, 更容易收到误差以及虚假量测的干扰。
5 结束语
文中对水下多目标跟踪数据关联方法的研究循序渐进, 结合纯方位系统的特点, 改进得出适用于双站纯方位多目标跟踪的MNNF算法和MPDA算法, 以减少计算量并保障多目标跟踪的精度, 以及克服纯方位角双站系统交叉定位产生的“鬼点”问题。其中, MPDA算法通过对跟踪门内公共量测做统一的弱加权处理, 减弱虚假量测值对于多个目标的影响, 减少误跟的概率。经比较发现, MPDA算法精度可以满足工程上的要求, 并在量测误差增大时远远优于MNNF算法。但是随着目标数量的不断增多, 交叉定位会导致量测数据的进一步扩大, “鬼点”数量也会急剧增加, 其滤波效果也会受到影响。此外, 量测角误差大小对于试验的结果影响较为明显, 如何消除这些虚假量测点并减少计算量, 以及减少量测误差带来的负面效果是今后研究的方向。
[1] Gavish M, Weiss A J. Performance Analysis of Bearing- only Target Location Algorithms[J]. IEEE Transactions on Aerospace & Electronic Systems, 1992, 28(3): 817-828.
[2] 夏佩伦. 纯方位目标跟踪系统的可观测程度[J]. 火力与指挥控制, 1992, (2): 25-31.
[3] 石章松, 刘忠. 单站纯方位目标跟踪系统可观测性分析[J]. 火力与指挥控制, 2007, 32(2): 26-29.
Shi Zhang-song, Liu Zhong. The Analysis of the Observability on the Single Platform Bearings-only Target Tra- cking System[J]. Fire Control and Command Control, 2007, 32(2): 26-29.
[4] 刘健, 刘忠, 玄兆林. 纯方位两站协同目标运动分析算法研究[J]. 舰船科学技术, 2006, 28(1): 64-69.
Liu Jian, Liu Zhong, Xuan Zhao-lin. Algorithms of Bearings-only Target Motion Analysis by Two Observers[J]. Ship Science and Technology, 2006, 28(1):64-69.
[5] Ho K C, Chan Y T. An Asymptotically Unbiased Estimator for Bearings-only and Doppler-bearing Target Motion Analysis[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 809-822.
[6] Nardone S C, Aidala V J. Observability Criteria for Bearings-Only Target Motion Analysis[J]. IEEE Transactions on Aerospace & Electronic Systems, 1981, AES-17(2): 162-166.
[7] Singer R A, Sea R G. A New Filter for Optimal Tracking in Dense Multitarget Enviroment[C]//The Ninth Allerton Conference Circuit and System Theory: Illinois, USA, 1971: 201-211.
[8] Song T L, Dong G L, Ryu J. A Probabilistic Nearest Nei- ghbor Filter Algorithm for Tracking in a Clutter Enviro- nment[J]. Signal Processing, 2013, 85(10): 2044-2053.
[9] Boumediene M, Ouamri A, Dahnoun N. Lane Boundary Detection and Tracking using NNF and HMM Approaches[C]//2007 IEEE Intelligent Vehicles Symposium. San Diego: IEEE, 2007.
[10] Bar-Shalom Y, Tse E. Tracking in Cluttered Environment with Probabilistic Data Association[J]. Automatica, 1975, 11(5): 451-460.
[11] Chang K C, Bar-Shalom Y. Distributed Adaptive Estimation with Probabilistic Data Association[J]. Automatica, 1989, 25(3): 359-369.
[12] Kirubarajan T, Bar-Shalom Y. Probabilistic Data Association Techniques for Target Tracking in Clutter[J]. Proc- eedings of the IEEE, 2004, 92(3): 536-557.
[13] 吴佳芯. 多目标跟踪的数据关联算法研究[D]. 西安: 西安电子科技大学, 2013.
[14] Bar-Shalom Y. Tracking and Data Association[M]. San Diego, CA: Academic Press Professional, 1987.
[15] Musicki D, Evans R. Joint Integrated Probabilistic Data Association: JIPDA[J]. IEEE Transactions on Aerospace & Electronic Systems, 2004, 40(3): 1093-1099.
Song T L, Kim H W, Musicki D. Iterative Joint Integrated Probabilistic Data Association for Multitarget Tracking[J].IEEE Transactions on Aerospace & Electronic Systems, 2015, 51(1): 642-653.
[16] 郭晶, 罗鹏飞. 密集杂波环境下的数据关联快速算法[J]. 航空学报, 1998, 19(3): 305-309.
Guo Jing, Luo Peng-fei. Fast Algorithm for Data Assoc- iation in Dense Clutter[J]. Acta Aeronautica et Astronau- tica Sinica, 1998, 19(3): 305-309.
[17] 刘俊, 刘瑜, 何友, 等. 杂波环境下基于全邻模糊聚类的联合概率数据互联算法[J]. 电子与信息学报, 2016, 38(6): 1438-1445.
Liu Jun, Liu Yu, He You, et al. Joint Probabilistic Data Association Algorithm Based on All-neighbor Fuzzy Clu- stering in Clutter[J]. Journal of Electronics &Technology, 2016, 38(6): 1438-1445.
[18] Julier S, Uhlmann J, Durrantwhyte H F. A New Method for the Nonlinear Transformation of Means and Covarian- ces in Filters and Estimators[J]. IEEE Trans Automatic Control, 2000, 45(3): 477-482.
(责任编辑: 杨力军)
Data Association Algorithm for Multi-target Tracking of Underwater Bearings-only Systems with Double Observation Stations
SU Jun, LI Ya-an, CHEN Xiao, ZHAO Zhen-yi
(School of Marine Science and Technology, Northwestern Polytechnical University, Xin’an 710072, China)
The bearings-only systemdouble observation stations generates a mass of false-location while locating multiple targets, which result in squared growth in the number of target measurement data and the number of false measurements. To solve this problem, this paper proposes modified nearest neighbor filter(MNNF) by adding a set of events according to nearest neighbor filter(NNF) with consideration of the fact that there is no effective measurement in the tracking gate. Then a modified probabilistic data association(MPDA) algorithm is also proposed by simplifyingthe calculation procedure of the joint probabilistic data association(JPDA) algorithm and weakly weighting all of the measurements in common area. Simulation is conducted to compare MPDA and MNNF, and the results show that both algorithms can help obtain satisfactory estimation result in the existence of “ghost points” in the bearings-only system with double observation stations, but MPDA performs obviously better than MNNF.
underwater multi-target tracking; bearings-only; data association; double observation stations
苏 骏(1990-), 男, 在读博士, 研究方向为水下目标跟踪.
TJ630.34; TB566
A
2096-3920(2018)02-0115-07
苏骏, 李亚安, 陈晓, 等. 双观测站水下纯方位多目标跟踪的数据关联算法[J]. 水下无人系统学报, 2018, 26(2): 115-121.
2018-02-07;
2017-03-07.
国家自然基金“超低信噪比水下目标信号的混沌阵子检测方法研究”项目资助(11574250).
10.11993/j.issn.2096-3920.2018.02.003

