基于北斗GEO卫星反射信号的海冰反演技术研究

孟婉婷,秦 瑾,张 云,周 勃

(1. 上海航天电子技术研究所，上海 201109； 2. 上海海洋大学 信息学院，上海 201306)

0 引言

海冰主要出现在极地以及部分高纬度区域，对我国来说，纬度偏高的地区主要有渤海海域以及黄海北部海域，这些区域因海冰灾害而受到巨大损失[1]。海冰灾害的出现，会损坏近海附近的沿岸设施，影响船只的来往通航，阻碍海洋捕捞以及海上油气资源的开发等，因此检测海冰成为防灾减灾的重要任务。

GNSS反射信号技术，也称为GNSS-R技术，是在全球导航卫星系统(Global Navigation Satellite System，也称为GNSS)的基础上发展起来的，是利用从海面反射回来的GNSS信号探测海面参数信息的遥感技术。此项技术能提供大量信号源及精准的时间、空间信息，且不受云、雨、雾等天气因素的影响[2]。近年来，该技术逐渐成为检测海冰的研究热点[3-7]。

由于海水与海冰反射面的复介电常数不同，基于GNSS-R技术检测海冰主要有两类检测模型：一类是欧空局的Fabra等[8-9]学者建立的偏振比反演模型(R-RHCP/R-LHCP)，另一类是国内的张云、孟婉婷等[10-11]建立的极化比反演模型(R-LHCP/D-RHCP)。偏振比反演模型是采用反射左旋信号(R-LHCP)与反射右旋信号(R-RHCP)反演海冰密集度的比值模型，而极化比反演模型是采用反射左旋信号(R-LHCP)与直射右旋信号(D-RHCP)反演海冰密集度的比值模型。

文献[10]中从原理维度分析了极化比海冰模型探测海冰的可行性，以及两个模型的适用范围，论述了偏振比模型适用于低仰角范围，而极化比模型适用于高仰角范围，但未从实验维度进行验证。本文结合上述两种反演模型，用菲涅尔原理对海冰反演特性进行了研究，并在渤海区域进行了相关实验，利用北斗卫星实验数据，对两种海冰反演模型在渤海海冰反演进行实验验证。

1 菲涅尔反射原理

假设海面是理想的镜面状态下，电磁波将发生镜面反射，入射角等于反射角，此时可以通过菲涅尔反射定律来描述。其反射信号的功率大小以及相位等信息，取决于GNSS入射波的频率、极化方式、入射角和反射面的性质(介电常数和电导率)。直射信号在经过海面散射后，反射信号输出功率的波形表达式[12]如下所示

式中：Ti为相干积分时间；R为菲涅尔反射系数；c为光速；R0为GNSS卫星到接收机的距离；R为卫星到海面上镜面反射点的距离；D为天线方向的有效覆盖区；Λ为等延迟区；S为等多普勒区；P为闪耀区；ρ为散射元。

由式(1)可知，影响反射信号输出功率波形的有反射与直射信号之间的路径延迟、GNSS卫星仰角、菲涅尔反射系数等。而本文后续所开展的实验都在类似的实验条件下进行，所以反射信号输出功率几乎不受反射与直射信号的路径延迟、GNSS卫星仰角的影响，但实验中海面的性质和菲涅尔系数有很大的不同，所以其反射信号输出功率很大程度上取决于菲涅尔反射系数[10]，其公式如下

(2)

(3)

(4)

(5)

式中：R为右旋圆极化分量；L为左旋圆极化分量；V为垂直线极化分量；H为水平线极化分量；ε为反射介质的复介电常数；θ为卫星仰角。

文献[10]中论证了渤海海域海水的复介电常数ε=75.54+48.27j，初生海冰的复介电常数平均数|εsi|=10，通常取ε=7.07+7.07j。根据上述复介电常数，对渤海海域内海冰和海水的菲涅尔反射系数进行仿真。海冰和海水情况下，菲涅尔反射系数和GNSS卫星仰角间的关系如图1、图2所示。

反射左旋信号分量随GNSS卫星仰角的增大而增大，反射右旋信号分量随GNSS卫星仰角的增大而减小。当仰角参数大于一个特定值(海水情况下约6.8°，海冰情况下约17.8°)的时候，左旋反射信号分量会大于右旋反射信号的分量。此时，说明GNSS卫星的直射右旋信号大部分转化为反射的左旋信号。

在仰角处于20°～45°时，海水情况下的反射左旋信号的菲涅尔反射系数(0.75～0.81)远大于海冰情况下的反射左旋信号的菲涅尔反射系数(0.43～0.52)。无论在海水还是海冰情况下，GNSS卫星直射的右旋信号的振幅趋近于相同，根据菲涅尔反射系数，海水的极化比值应大于海冰的极化比值。

高仰角时，由于反射右旋信号的分量远小于反射左旋信号的分量，此时，偏振比值趋近于零，很难比较出海水与海冰情况的不同，因此，偏振比模型更适用于低仰角。而对于高仰角来说，由于不同反射面情况下，反射左旋信号的分量差值较大，极化比值模型更加适用于高仰角。

2 实验设置

为了通过实验验证上文中所提到的海冰极化比模型是否能反演海冰变化的过程，以及两类海冰反演模型的适用范围，2015年1月24日，在中国天津汉沽的海冰观测站的岸基旁，开展了基于北斗反射信号的渤海岸基实验，并搭建直射、反射天线及GNSS-R软件接收机。海冰观测站及实验区域如图3所示。

实验采用北斗系统的静止卫星，因为其仰角不变，消除了仰角变化对实验结果的影响，采用极化比模型实现对渤海海冰变化趋势的反演。

直射与反射天线架设在离海水表面约7.6 m高度的支架上。本次实验用到了3种天线，天线的技术参数见表1。直射右旋天线朝向天空水平架设，采集北斗卫星的直射右旋信号，反射左旋天线与反射右旋天线倾斜朝向海面并朝南放置(反射左旋天线与反射右旋天线的倾斜角度相同)，采集海面反射回来的反射左旋信号和反射右旋信号。直射和反射天线示意图如图4所示。

GNSS反射信号技术所采用的接收机是采集实验区域反射面信息的主要设备，其目的是获取来自反射面的GNSS直射信号与反射信号，并具备2种信号的频率变化、数字化(采集和量化)、跟踪捕获卫星信息、对数据进行后处理等功能[8]。对GNSS-R接收机来说，一般分为硬件和软件两种。本次实验中，接收机设备是北京航空航天大学研制的第二代软件接收机，如图5所示。其软件接收机有4个通道，本次实验选择了其中的3个通道，采集D-RHCP信号、R-LHCP信号和R-RHCP信号，采集频率是16.36 MHz，传输速率是16 MB/s。

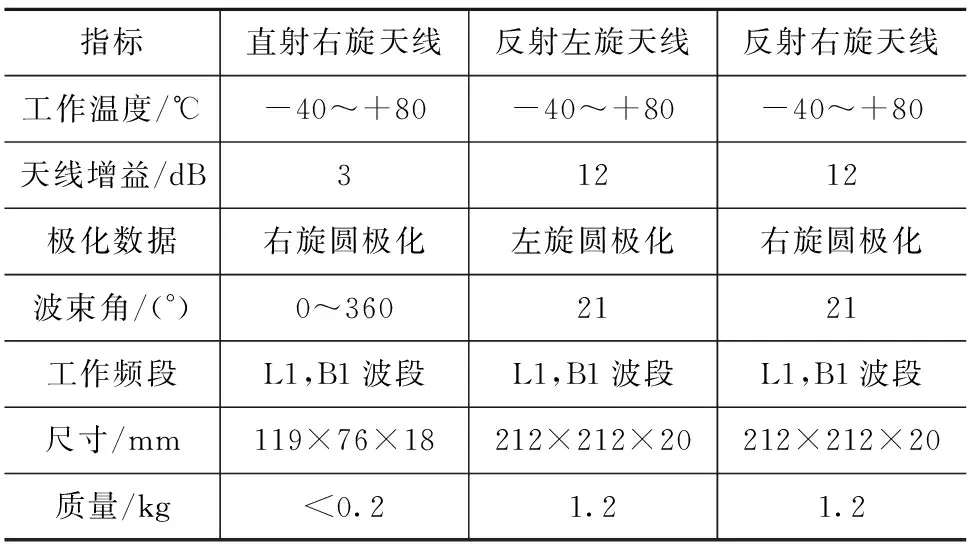
表1 D-RHCP天线/R-LHCP天线/R-RHCP天线参数对比

3 对比数据

为了和GNSS-R实验结果进行对比分析，在实验过程中，对比数据采用实验现场的海冰密集度信息(现场照片的SVM分析结果)，以及附近气象站的数据(潮汐和气温：主要影响海冰变化的两个因素)。

对所采集的实验场地照片，本文使用图像处理方法(支持向量机，也称为SVM)计算图片中的海冰密集度，结果如图6所示[14]。图6中，紫红色的点表示每10 min的海冰密集度测量值。图中照片为不同时间下的实验场景，分别是08:09，10:39，12:14，14:54，15:59，16:32。

对于气象站记录的潮汐数据，2015年1月24日，渤海海域是半日潮。最高潮的时间分别是05:48和17:33，最低潮的时间是12:09。实验期间，12:00～13:00，温度到达最高之后再下降，观测区域有短暂融冰再结冰的现象。

实验现场的海冰密集度如图6所示。07:58～12:14，无明显变化；12:14后，由于气温上升再下降，海冰密集度有一个下降再略微上升的过程；13:06～15:16，海冰密集度的改变较平稳；15:16后，因为潮水涨到实验区域，潮水击碎海冰，海冰渐渐随涨潮融化为海水，直到实验结束。

4 实验分析

根据天线朝向及观测的海域，本文选择仰角范围为20°～45°，方位角范围为135°～225°的卫星。符合实验条件的是北斗C01号和C03号卫星(仰角分别为38°和43°)。这两颗卫星是静止轨道卫星，也称为GEO卫星。GEO卫星静止投影在地球的赤道上，其仰角不变，消除了仰角对实验结果的影响。

计算实验数据的极化比值，结果如图7所示。图7给出了2015年1月24日07:58～16:43的每一组数据的极化比值，图中红色实线为北斗C01号卫星的极化比值，蓝色实线为北斗C03号卫星的极化比值，紫红色虚线为海冰密集度的趋势。底部窗口中，紫红色柱状图为实验区域的空气温度(气象站数据)，X轴表示时间序列，Y轴表示温度。

文献[14]中论述了极化比值与海冰密集度成反比。图7中，北斗C01号卫星的极化比值在12:45前后有一个略微上升再下降的过程，与海冰密集度的趋势相似；极化比值在15:16后一直上升到实验结束，与海冰密集度的变化趋势相似。北斗C03号卫星的极化比值在12:55后没有观测到明显变化；但在15:16后，一直上升到实验结束，这一段趋势与海冰密集度相似。

由上述结果可见，北斗C01号卫星的极化比值与海冰密集度有良好的一致性，在12:55后，因为受到温度影响，海冰有一个短暂融化再冻结的过程。而北斗C03号卫星并没有这个趋势，有可能是因为C03号卫星的镜面反射区域含有大量的泥沙和石子，影响观测结果。北斗C01号和C03号卫星的极化比值在15:16后都有上升的情况，这是因为海水涨潮，到达实验区域，使海冰融化，逐渐变成海水引起的。

由上述分析，计算实验数据的偏振比值，结果如图8所示。图中给出了实验期间每一组数据的偏振比值，图中红色实线为北斗C01号卫星的偏振比值，蓝色实线为北斗C03号卫星的偏振比值。

文献[15-17]中论述了偏振比值与海冰密集度成正比。图8中，北斗C01号卫星的偏振比值在中午前后有一个下降再上升的过程，北斗C03号卫星的偏振比值在中午前后有一个略微下降再上升的过程，与海冰密集度的趋势较类似。C01号卫星的偏振比值在13:58后一直下降，到实验结束，C03号卫星的偏振比值在15:16后也有一个略微下降的趋势，到实验结束。实验结果汇总见表2。

根据前文对两种海冰模型的反演结果分析，极化比值和海冰密集度有较强的相关性。实验成功反演了海冰的两次变化趋势(海冰短暂融化再冻结的过程以及完全融化的过程)，偏振比值虽然有类似的变化趋势，但受到的影响较大。本次实验选取的卫星仰角较高，结合菲涅尔反射原理，当海面特性产生微小变化时，偏振比值变化较大，很难反演出是短暂融冰还是完全融冰，这也验证了理论部分对于极化比值模型更适用于高仰角的分析。

表2 实验结果汇总表

5 结束语

本文根据涅尔反射系数原理，对渤海海域的菲涅尔反射系数(海水、海冰)进行了仿真，分析了极化比海冰反演模型的适用范围。卫星仰角较高时，不同反射面的反射左旋信号分量区别较大，极化比值的变化也较大，能较好地反演不同反射面的特性。而偏振比值趋近于零，不能很好地反演出反射面的特性变化。

本文还介绍了2015年1月在渤海岸基海冰观测站前开展的渤海实验，通过对实验数据的分析结果可以看出，极化比值和海冰密集度有很强的相关性，实验成功地反演了海冰的变化趋势，反演出了海冰短暂融化再冻结的过程以及完全融化的过程。

实验验证了利用北斗反射信号反演海冰的可行性。同时，对比了极化比模型与偏振比模型的实验结果，验证了两种模型的仰角适用范围。可以利用极化比海冰反演模型来弥补偏振比海冰反演模型在高仰角情况下的不稳定，改善海冰反演模型在海冰检测中的准确性，为定量反演海冰区域的海冰密集度的研究打下了基础，也为海冰灾害预警提供了一种新的手段，同时拓宽了北斗卫星的应用范围。

[1] 刘煜, 刘钦政, 隋俊鹏, 等. 渤、黄海冬季海冰对大气环流及气候变化的响应[J]. 海洋学报(中文版), 2013, 35(3): 18-27.

[2] 张云, 郭建京, 洪中华, 等. 基于GPS反射信号的岸基海冰探测研究[J]. 极地研究, 2014, 26(2): 262-267.

[3] KOMJATHY A, MASLANIK J, ZAVOROTNY V U, et al. Sea ice remote sensing using surface reflected GPS signals [M]. Remote Sensing Symposium, Honolulu Hawaii, 2000.

[4] WIEHL M, DIETEICH R, LEGRÉSY B. Potential of reflected GNSS signals for ice sheet remote sensing[J]. Progress in Electromagnetics Research, 2003, 40(7):177-205.

[5] GLEASON S, HODGART S, SUN Y, et al. Detection and processing of bistatically reflected GPS signals from low Earth orbit for the purpose of ocean remote sensing[J]. IEEE Transactions on Geoscience& Remote Sensing, 2005, 43(6):1229-1241.

[6] RIVAS M B, MASLANIK J A, AXELRAD P. Bistatic scattering of GPS signals off arctic sea ice[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1548-1553.

[7] LI W, CARDELLACH E, FABRA F, et al. First spaceborne phase altimetry over sea ice using TechDemoSat-1 GNSS-R signals[J]. Geophysical Research Letters, 2017, 44(16): 8369-8376.

[8] FABRA F, CARDELLACH E, RIUS A, et al. Phase altimetry with dual polarization GNSS-R over sea ice[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(6): 2112-2121.

[9] FRAN Fabra. GNSS-R as a source of opportunity for remote sensing of the cryosphere[D]. Instituto de Ciencias del Espacio (ICE-CSIC/IEEC), 2013.

[10] 张云, 孟婉婷, 顾祈明, 等. 基于GPS反射信号技术的渤海海冰实验[J]. 海洋学报(中文版), 2014, 36(11): 64-73.

[11] YUN Z, WANTING M, QIMING G, et al. Detection of bohai bay sea ice using GPS-reflected signals[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(1): 39-46.

[12] ZAVOROTNY V U, VORONOVICH A G. Scattering of GPS signals from the ocean with wind remote sensing application[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(2): 951-964.

[13] 公绪艳. 基于GNSS反射信号的海面风场反演方法研究[D]. 北京化工大学, 2016.

[14] 孟婉婷. 基于GNSS反射信号的海冰检测的研究[D]. 上海海洋大学, 2016.

[15] 张云, 郭建京, 袁国良, 等. 基于GNSS反射信号的海冰检测的研究[J]. 全球定位系统, 2013, 38(2): 1-6.

[16] 邵连军. 利用GNSS-R信号探测海冰的方法及初步实验结果[J]. 遥感信息, 2013, 28(2): 12-15.

[17] 杨明华, 曹云昌. 基于GNSS-R的后续海冰观测实验[J]. 全球定位系统, 2014, 39(4): 51-54+68.