数学困难儿童估算策略运用的中央执行负荷效应*

杨伟星 张堂正 李红霞 张佳佳 司继伟

(山东师范大学心理学院,济南 250358)

1 引言

人类认知加工的一个重要方面便是个体的表现依赖于其所用策略(Uittenhove &Lemaire,2012)。策略指为达到某个更高水平目标或完成某个任务所采取的单个或一组认知加工程序(Si,Li,Sun,Xu,&Sun,2016)。策略运用是个体如何选择并使用特定策略解决问题的过程(Lemaire &Lecacheur,2011)。策略运用分为策略执行和策略选择,前者指个体使用给定策略解决问题的时间和正确率(Mata,Josef,&Lemaire,2015),可以比较不同策略解决问题的效能差异以及不同个体有效执行策略的能力差异,后者指个体在某一情境中如何选择合适策略有效地解决问题。现有大量证据表明,中央执行(黄碧娟,封洪敏,司继伟,张杰,王翔艳,2016;司继伟,杨佳,贾国敬,周超,2012)、年龄(Si et al.,2016)、认知风格(司继伟,刘亚琼,贾国敬,黄碧娟,2016)、策略效率和难度(Hinault,Dufau,&Lemaire,2014;Uittenhove &Lemaire,2012)、策略使用顺序(Hinault,Lemaire,&Phillips,2016;Hinault,Lemaire,&Touron,2017)、任务难度和问题情境(Hinault et al.,2014;Xu,Wells,Lefevre,&Imbo,2014)、文化差异(Xu et al.,2014)等内外因素都会不同程度地影响策略运用。因此,个体在面对具体任务时会倾向于适应性地选择最佳策略来完成各种认知操作(艾继如,张红段,司继伟,卢淳,张堂正,2016;Mata et al.,2015)。本研究主要关注中央执行对个体策略运用的影响。

目前一般认为,中央执行作为工作记忆系统中最复杂的成分,主要起过程控制的作用,对认知活动会产生重要影响(艾继如等,2016)。而对这一问题的探讨主要分为两个方面：一是侧重于揭示中央执行子成分对策略运用造成的差异性影响,如转换(Ardiale &Lemaire,2013)、抑制、刷新(Lemaire &Lecacheur,2011)等。另一方面则侧重于通过双任务范式考察中央执行负荷对策略运用过程的具体影响(黄碧娟等,2016;司继伟等,2012)。而在算术认知领域中,对中央执行功能参与算术认知活动的研究大多采用双任务实验范式。有研究发现,中央执行负荷会降低儿童在算术认知中的策略执行效果,对简单和复杂任务都会产生整体性影响(王明怡,陈英和,2006)。Imbo,Duverne 和 Lemaire (2007)也发现,中央执行负荷会导致成人的策略执行变差,且上调策略比下调策略的表现更差,也会影响策略选择,因为存在中央执行负荷时,各种策略对认知资源的竞争变得更为激烈,个体会更多选择占用认知资源较少的简单策略,而非最佳策略,说明中央执行参与了策略运用过程。而一些关于个体策略运用随着年龄而变化的研究也在某种程度上证明了中央执行参与了策略运用,因为策略运用的提高可能是因为中央执行功能发展的结果,随着年龄增长,儿童的策略选择表现明显提高,而中央执行在不同年龄段均存在显著预测效应(丁晓,吕娜,杨雅琳,司继伟,2017)。Lemaire 和 Calliès (2009)曾发现,个体的策略运用与年龄变化相关更大,他们认为这可能是因中央执行功能发展所致。Lemaire和Lecacheur(2011)的研究则显示,中央执行在策略运用的年龄相关差异中起着中介作用,且中央执行功能的得分与选择最佳策略的比例存在一定程度的相关。此外,中央执行负荷对成人的策略选择、执行及策略选择适应性都产生了影响,高负荷条件下个体的策略选择适应性更差(司继伟等,2012)。这说明中央执行功能参与策略运用过程并对其产生重要影响。但前人这些研究大多采用相关设计,直接检验中央执行功能在个体策略运用中的作用的实验操纵还相当罕见。

估算属于算术估计类型的一种,是个体未经精确计算而只借助原有知识对问题提出粗略答案的一种估计形式(艾继如等,2016)。作为一直以来被高度强调精算教学的学校数学教育所忽视但重要的算术技能,估算被看作是考察个体策略运用灵活性和多样性的有效工具,同样反映了个体的数学成就。而能否灵活选择估算策略解决问题不仅是个体认知灵活性的重要标志,也是影响估算能力和整个估算加工过程的关键,这与中央执行功能之间存在着高度关联(艾继如等,2016;黄碧娟等,2016;司继伟等,2012)。

在以往探讨中,研究者往往侧重于中央执行对正常儿童或成人算术策略运用的影响(刘昌,2004;司继伟等,2012),但忽视了关注数学困难儿童这一“特殊群体”。一般来说,数学困难(mathematical disability,简称 MD)是指儿童具有正常智力,没有明显神经或器质性缺陷,但在标准数学测验上的得分低于正常学生,是学龄儿童较为普遍的一种学习困难类型(Fletcher,Stuebing,Morris,&Lyon,2013)。根据不同国家采用的MD诊断标准的不同,数困影响着大约3.5%～13.8%的正常智力的学龄儿童(华晓腾,司继伟,卢淳,2012;李红霞,司继伟,陈泽建,张堂正,2015)。考虑到中国庞大的人口基数,对我国数困儿童的估算策略运用进行研究具有重要的理论和现实意义。以往研究发现,数困儿童在估算任务中的表现远不如学优儿童,对估算策略运用的有效性和灵活性均比正常组儿童差,策略选择的适应性显著低于正常组儿童(Torbeyns,Verschaffel,&Ghesquière,2004a,2004b)。由此可见,数困组儿童的策略运用表现一般都不如正常组儿童,但具体原因仍不清楚。有学者认为,数困儿童的情感因素方面可能存在问题(Passolunghi,2011),但Desoete和De Weerdt (2013)从认知角度对数困儿童进行研究,则发现工作记忆,特别是中央执行,对数困儿童的行为抑制特别重要。张树东和董奇(2012)也发现,存在数字加工和计算困难的学生,往往有明显的中央执行功能障碍。对此,Geary (2004)认为,个体的数学能力主要包括两部分,概念性知识的累积和解决具体问题的程序性知识的运用,两者都需要中央执行功能的支持。数困儿童的通常表现是概念知识或者是运算程序上的困难,而这两者最终应归结于中央执行功能的障碍。较差的中央执行功能可能无法有效抑制额外干扰,这在某种程度上可能阻碍了数困儿童策略运用的表现。上述推测在一些研究中已得到某些证实(Passolunghi &Siegel,2004;Passolunghi,2011)。总之,研究者已就数困儿童的中央执行功能较差,从而无法抑制与任务无关的信息干扰的观点取得了较一致的认识。

然而,以上研究虽然证实了较差的中央执行功能可能会在一定程度上导致数困儿童较差的算术策略运用,但这些研究大多采用相关设计,对于中央执行功能如何影响数困儿童的策略运用却缺乏进一步直接的实验研究,而将执行功能分离开来研究也有所片面,因此,对中央执行进行整体性操控可以更全面地理解其对个体策略运用过程的具体影响(司继伟等,2012)。此外,前人研究忽视了不同中央执行负荷水平对数困儿童估算策略运用可能存在不同影响,如果能严格操控负荷水平,或许会发现数困儿童与正常儿童在估算策略运用中更深层次的差异。即两组儿童的策略运用都会受到负荷影响,但随着负荷的增加,两组儿童所受影响会发生变化,数困儿童受到的影响可能会相对更大。考察中央执行负荷对数困儿童估算策略运用的影响,不仅可以揭示数困儿童与正常组儿童的估算策略运用存在差异的原因,也有助于丰富和完善对中央执行功能在个体策略运用以及数学认知中所起作用的认识。此外,虽然国外也有少量类似研究(Torbeyns et al.,2004a,2004b),但是鉴于估算策略运用存在跨文化差异(Imbo &LeFevre,2009,2011;Xu et al.,2014),因此,以数困儿童为研究对象开展探讨对于中国这一人口基数庞大的国家来说显得尤为重要。

鉴于前人的研究发现,二、三年级的数困儿童可能还存在某些基本数字知识和概念性知识的困难,不能完全理解计算原理,且在基本加减乘除的算术事实提取中也可能存在困难(黄大庆,陈英和,2016),这会混淆研究结论,从而分不清到底是中央执行功能较差还是数学认知能力较差导致数困儿童的估算策略运用较差。此外,儿童估算策略最重要变化可能出现在四、六年级之间(Lemaire,Lecacheur,&Farioli,2000;Si et al.,2016),并且,考虑到中国小学生的实际情况,六年级是小升初的过渡阶段(也可能是因为这一阶段的特殊性,研究者或者被试的监护人或者校方担心影响儿童升学,所以相关的研究相对稀少),考察中央执行负荷对数困儿童估算策略运用的影响不仅可探明其策略运用较差的原因从而更好地服务于这一群体,也能为提高数困儿童在数学运算中的策略运用以及为更好地面对初中时期的数学学习提供指导。因此,本研究选取了数学知识经验较丰富的六年级这一特殊时期的儿童作为被试。此外,本研究采用高、低、无三种负荷条件可以避免先前研究只研究有无负荷的局限性,因为低负荷任务主要是保持信息,高负荷任务需要信息操作与更新,这会在更大程度上激发中央执行的参与程度(司继伟等,2012)。本研究拟采用数困儿童和数学能力正常发展的对照组为被试,采用选择/无选法范式,通过设置无、低、高三种负荷条件的材料,更全面揭示中央执行负荷对数困儿童算术策略的运用(包括策略选择,策略执行和策略适应性)的影响,以此考察其策略运用较差的可能原因,即数困儿童的中央执行功能可能存在障碍,不能有效抑制额外干扰并合理分配认知资源,从而导致较差的策略运用。我们假设,随着负荷的增加,两组儿童的策略运用整体表现都会变差,但数困儿童的表现不同于正常组儿童,且可能受到负荷较大影响。

2 方法

2.1 被试

参照前人标准选取数困儿童(刘昌,2004)：(1)先筛选出两所乡镇小学6年级儿童最近两次校级以上考试数学平均成绩在后25%,为确保筛选出的数困儿童不是因为阅读能力受限而导致数学学习困难,同时要求数困儿童的语文平均成绩要在前50%;(2)再对这些儿童实施瑞文标准推理测验,排除智力得分低于80的儿童;(3)然后采用临床诊断法,将筛选出的儿童名单交给班主任和各科目代课老师进行确认,排除那些具有明显感官缺陷和情绪障碍的儿童,最后即为本研究选取的数困儿童;(4)按名册随机抽取另外一部分 6年级儿童作为正常组儿童。总共从11个班级的657名6年级儿童中筛选出数困儿童40名(检出率约为6.09%)以及正常组儿童 40名,最后完成实验的有效被试为：数困儿童36名(男20名;平均年龄11.75岁);正常组儿童38名(男18名;平均年龄11.60岁)。需要说明的是,本研究与黄大庆和陈英和(2016)采用自编的数学认知能力问卷对数困儿童的检出率3.32%存在一定出入,这是可以理解的。为使本研究所关注的数困儿童既不偏离数学困难的定义,也能使研究结果更切合小学教学,同时不脱离数学认知活动所依赖的背景和任务,我们采用了与儿童提高的认知能力以及变化了的数学任务相对应的6年级校级数学考试这一数学认知能力测验来筛选数困儿童。这可能是检出率存在一定出入的原因。所有被试之前未接触过类似实验,视力正常或矫正视力正常,实验结束后赠送一份小礼物。

2.2 实验设计

采用2(被试类型：数困组儿童、正常组儿童) ×3(任务类型：高负荷、低负荷、无负荷)×3(策略运用条件：最佳选择、无选上调、无选下调)三因素混合实验设计,其中被试类型为被试间变量,任务类型和策略选择条件为被试内变量,因变量是被试的策略运用效率,包括策略执行的反应时和正确率、策略选择的反应时和正确率以及策略选择适应性的正确率。

2.3 实验材料

2.3.1 主任务材料

30道两位数加法估算问题,均为混合问题(一个加数个位小于5,另一个大于5,如53 + 48),其中15道下调题(个位不进位,41 + 76),15道上调题(个位进位,43 + 78)。一半问题的第一个加数个位数大于 5,第二个加数个位数小于 5,另一半问题相反。一半问题较大的加数在左侧(63 + 28),另一半在右侧(18 + 73)。根据前人研究(Lemaire &Calliès,2009),在确定加法题目时我们还注意了以下几点：(1)加数的个位数不包含0或者5;(2)同一问题中,两个加数的十位数或个位数不能重复(64 + 24);(3)加数个位与十位数不能重复(66 + 31);(4)不能用一个问题的两个加数换位作另一问题(若有32 + 47就不能再有47 + 32);(5)两个加数不能相同(23 + 23)。题目随机呈现。

2.3.2 次任务材料

对次任务材料的选取,不同研究的结论不同。司继伟等人(2012)假设,次任务类型会影响心算表现,估算与阿拉伯数字信息的操作会占用同一种认知资源(一致任务),而与字母信息的操作占用不同的认知资源(不一致任务),因此,阿拉伯数字作为次级任务对主任务(加法估算)的影响会比字母的影响更大。但研究结果发现,在反应时上,一致任务只有在高负荷下的干扰作用才大于不一致任务,在正确率上却未发现任何差异,即没有表现出不同次级任务对主任务的显著差异性影响。Han和 Kim(2004)对执行工作记忆是否影响视觉搜索的研究发现,主任务材料和次任务材料的一致性越高越能刺激被试的优势反应定势。综合考虑之后,我们选取了对主任务可能存在更大刺激的数字(一致任务)作为次任务材料。此外,结合算术认知领域(司继伟等,2012)以及其他认知领域对工作记忆容量的有关研究(程家萍,罗跃嘉,崔芳,2017),我们对高低负荷进行了相应的操纵,具体的次任务设置如下：(1)高负荷任务,随机依次呈现5个1～9中的阿拉伯数字,要求被试从大到小排列,然后按键回忆判断屏幕呈现的数字串是否正确;(2)低负荷任务,随机依次呈现3个0～9的阿拉伯数字,其它要求同(1);(3)无负荷任务,不呈现次任务材料。

2.3.3 瑞文标准推理测验

瑞文标准推理测验由英国心理学家瑞文(Raven)于1938年设计,是一种适用于6岁儿童到成人被试的非文字智力测验,有5个黑白系列,共计60个项目组成。本研究采用张厚粲于 1986年主持修订的瑞文标准型测验。对被试在教室里进行 40分钟的团体施测。

2.4 实验程序

实验程序由 E-prime 2.0软件编写,随机呈现刺激,计算机自动记录被试反应时(RT)和正确率(ACC)。基于选择/无选法范式的设计思想(司继伟,徐艳丽,封洪敏,许晓华,周超,2014;Xu et al.,2014),实验分为3种条件：(1) c1最佳选择条件,可以考察策略选择和策略选择适应性。要求被试必须从上调和下调策略中选择一种又快又准得出估算结果的策略来解决问题,如,23+48,被试可选择上调或者下调策略来解决,输入估算答案80和60都是策略选择的正确结果,但只有 80反映了策略选择适应性;(2) c2无选上调条件,要求被试必须使用上调策略来解决所有问题;(3) c3无选下调条件：要求被试必须使用下调策略来解决所有问题。有选条件能独立考察策略选择,而无选条件则独立考察策略执行。为避免无选条件下的策略执行影响选择条件下的策略选择,所有被试均按照 c1→c2→c3的顺序进行测验(司继伟等,2012)。每种实验条件间隔5分钟,每名被试需完成90个实验试次,正式实验之前告诉被试对于每道加法题都采用估算的方式解决。为确保被试理解实验程序和任务要求,正式实验之前有 8个练习试次,会有正误反馈,练习试次不会出现在正式试验中,且正式实验没有反馈。各负荷情境的具体实验程序如下：

(1) 高负荷实验：被试进行数字大小排序和估算任务。每位被试单独施测,视距保持60 cm,先在17英寸屏幕(屏幕分辨率为 800×600,刷新率为75 Hz)中央呈现红色注视点“+”,500 ms之后在同一位置随机依次呈现 5个 1～9的阿拉伯数字(灰底黑字,Times New Roman字体,48号),每个数字呈现200 ms,每个数字之后间隔500 ms,要求从大到小依次排序,所有数字呈现完之后,在屏幕中央呈现算术式(如,23 + 48) 1000 ms之后,被试需要对排序的数字先进行再认(正确按F键,错误按J键),然后输入估算结果,按回车键之后进入下一试次。实验流程详见图1。

(2) 低负荷实验：呈现 3个阿拉伯数字,其它设置同(1)。

(3) 无负荷实验：不呈现数字,其它设置同(1)。

图1 高负荷实验程序

2.5 数据统计与分析

使用SPSS 16.0和Excel 2010对所获数据资料进行统计分析。

3 结果

3.1 策略执行

选择/无选法中的无选条件可以无偏考察各种策略的执行时间和准确性,可以反映出各策略解决问题的相对优势。本研究中的c2和c3条件下的反应时和正确率分别反映了无选上调和无选下调策略的执行情况。我们只统计分析了被试按照指定策略正确解决问题的反应时。剔除了超过±3个标准差以外的反应时数据(剔除率 2.73%)。无选条件下被试要用给定的某一策略解决问题。根据输入的估算答案判断被试使用了何种策略,若使用了给定策略则编码为1,若没有使用则编码为0,我们只分析了编码为1的反应时数据。正确率即为编码为1的试次数/总试次数。c2和c3条件下的数据分别统计。

我们首先考察了被试在正确率和速度上的分配模式,分别对两组被试在无、低、高三种负荷条件下的正确率与反应时进行皮尔逊相关分析,发现,正常组中两者均不存在显著相关,r分别为-0.02、0.23、-0.01,ps >0.05,即不存在反应时与错误率的代偿,数困组中,r分别为-0.03、0.03、0.18,ps >0.05,也不存在反应时与错误率的代偿。

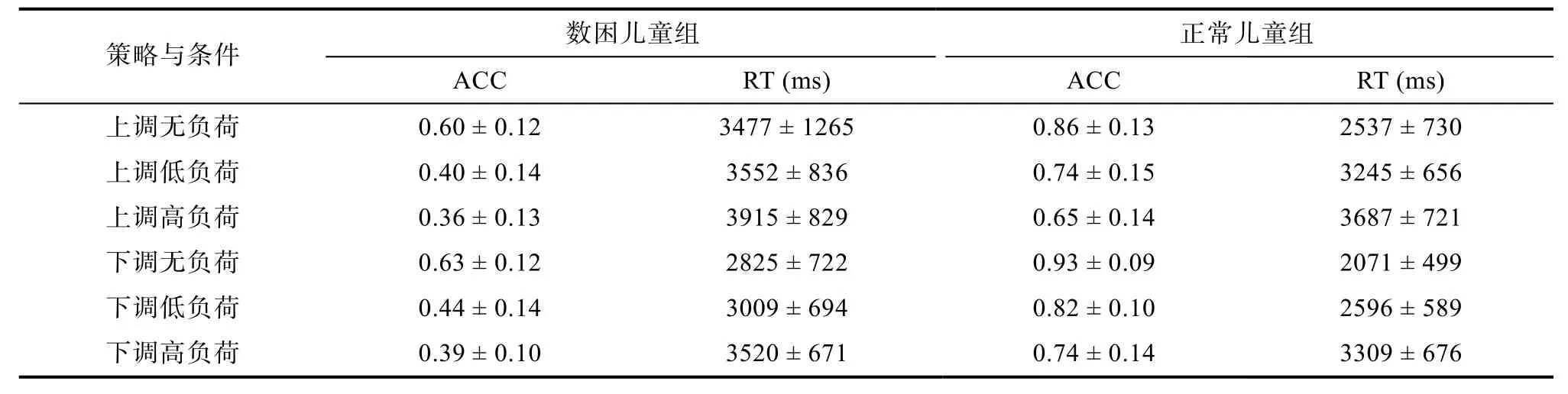
表1 策略执行的描述统计结果(M±SD)

图2 实验条件与被试类型在策略执行正确率上的交互作用

此外,为探究数困儿童和正常儿童的策略执行的表现受负荷影响的重要模式性差别,我们还比较了随着负荷的增加,两组儿童的中央执行功能差异的变化情况,即无、低、高负荷三种条件下的正常组与数困组在策略执行正确率上的差异的变化情况,对三种条件下的差值(三种条件下对应的的正常组的正确率减去数困组的正确率)进行了单因素方差分析。结果显示,三种负荷条件间差异显著,F(2,105)=3.18,p=0.045,η=0.054。多重比较显示,两组儿童之间的差值在低负荷之间的差异(0.36)显著大于在无负荷(0.28)之间的差异,p =0.01;虽然在高负荷之间的差异(0.33)大于在无负荷之间的差异(0.28),但未达到显著水平,p=0.14,高负荷与低负荷之间的差异也不显著,p=0.30。从图2也可以形象地看出,在无、低、高三种负荷条件下,两组的差异是先变大再基本不变,可能是高负荷对两组儿童来说认知负担都很大,导致正常组的表现也变得很差,从而使得差异不明显。此外,从图 2可以初步认为,随着负荷的增加,正常组以近似线性的变化,而数困组是非线性的。为了更可靠地比较两组儿童的中央执行功能对负荷增加所分别表现出的独特差异,我们还对两组儿童的正确率在三种负荷条件下的各自的变化程度(Δ)进行了分析。Δ的计算方法为,高负荷正确率(反应时)的Δ等于高负荷的正确率(反应时)减去低负荷的正确率(反应时),低负荷正确率(反应时)的 Δ等于低负荷的正确率(反应时)减去无负荷的正确率(反应时)。由此,我们对两组儿童的策略执行正确率的Δ进行了 2(被试类型：正常/数困组)×2(Δ：高负荷/低负荷)的两因素混合设计的重复测量方差分析,结果显示两者交互作用显著,F(1,72)=5.93,p=0.017,η=0.08。简单效应分析显示,正常组的Δ差异不显著,F(1,72)=1.20,p=0.28;数困组的Δ差异显著,F(1,72)=19.93,p <0.001;η=0.22,高负荷正确率的 Δ(0.10)显著小于低负荷正确率的 Δ(0.39),呈现出先增加后降低的趋势,从图 2也可以看出,低负荷Δ的斜率比高负荷的更加陡峭。这说明,正常组的策略执行表现的 Δ随着负荷的增加并未出现显著差异,即策略执行的表现以近似线性降低,但数困组的表现却随着负荷增加而以先快后慢的非线性趋势下降。

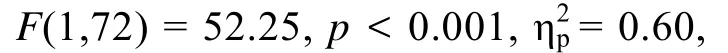
此外,我们分析了三种负荷条件下对应的正常组与数困组在策略执行反应时上差异的变化情况,对三种条件下的差值进行了单因素方差分析,结果显示,负荷条件之间差异显著,F(2,105)=3.18,p <0.001,η=0.16。多重比较显示,两组儿童在低负荷之间的差异(339 ms)显著小于无负荷之间的差异(841 ms),p=0.001;高负荷之间的差异(210 ms)虽然小于低负荷之间的差异(339 ms),但未达到显著水平,p=0.38;高负荷之间的差异显著小于无负荷之间的差异,p <0.001。此外,与正确率类似,正常组反应时随着负荷增加以近似线性的趋势变化,而数困组是非线性的,我们对两组儿童的策略执行反应时的Δ进行了2×2的重复测量方差分析,结果显示,二者交互作用边缘显著,F(1,72)=2.99,p =0.088,η=0.04。简单效应分析显示,正常组儿童的Δ差异不显著,F(1,72)=0.076,p=0.78;数困组儿童的Δ差异显著,F(1,72)=4.60,p=0.035;η=0.06,高负荷反应时的 Δ(308 ms)显著大于低负荷反应时的 Δ(143 ms),表现出不断变大的趋势,从图 3也可以看出,数困组中,高负荷的斜率比低负荷的更加陡峭。这表明,随着负荷增加,正常组的策略执行反应时以近似线性的趋势上升,而数困组却以不断加快的非线性趋势上升。从以上结果可看出,数困组有着区别于正常组的独特的中央执行负荷模式。

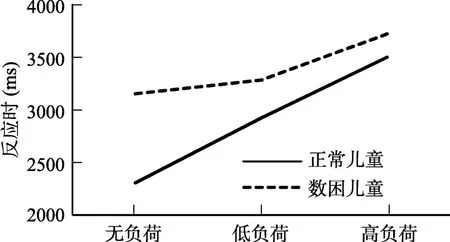
图3 实验条件与被试类型在策略执行反应时上的交互作用

3.2 策略选择

在本研究中,被试在条件 c1下的反应时和正确率反映了策略选择情况。根据被试输入的估算答案判断被试使用了何种策略。对策略选择的反应时数据编码如下：若被试使用上调策略编码为 1,使用下调策略则编码为2,使用其它策略则编码为0。本研究只分析编码为1和2的数据,编码为0的数据不予分析。剔除了超过±3个标准差以外的反应时数据(剔除率3.13%)。策略选择正确率的编码如下：若被试使用了给定的上、下调策略中的一种正确解决了问题,则编码为 1,若使用了其它策略(错误)则编码为0。如,解决23 + 48可以使用上调策略30 + 50=80或者下调策略20 + 40=60,都反映了正确的策略选择,策略选择的正确率为编码为1与2的试次数之和/总试次数。

我们首先考察了被试在正确率和速度上的分配模式,分别对两组被试在无、低、高三种负荷条件下的正确率与反应时进行皮尔逊相关分析,正常组中,发现两者均不存在显著相关,r分别为0.13、-0.14、0.007,ps >0.05,即不存在反应时与错误率的代偿,数困组中,r分别为-0.03、0.03、-0.1,ps >0.05,也不存在反应时与错误率的代偿。

表2 策略选择的描述统计结果(M±SD)

图4 实验条件与被试类型在策略选择正确率上的交互作用

图5 实验条件与被试类型在策略选择反应时上的交互作用

3.3 策略选择适应性

在本研究中,策略选择适应性指被试在策略选择过程中,选择了更接近于精确计算结果的策略,那么被试对这个策略的选择是适应性的(Lemaire,Arnaud,&Lecacheur,2004)。例如：对于86+43,使用下调策略可以得到更为精确的结果,若被试使用了下调策略80 + 40=120,那么就说明被试在该题的策略选择上具有良好的适应,若被试使用了上调策略90+50=140虽是正确的策略选择结果,但却不是适应性的。本实验有一个策略运用条件(c1)涉及策略选择的适应性。我们采用被试选择最佳策略的正确率来衡量策略选择的适应性(司继伟等,2012)。将选择适应性的策略编码为“1”,没有选择适应性的策略编码为“0”,策略选择适应性的正确率即为编码为1的试次数/总试次数,以被试类别作为被试间变量,以实验条件(高负荷、低负荷、无负荷)作为被试内变量,对两组儿童的策略选择适应性的正确率(见表 3)进行 2×3的重复测量方差分析。结果发现：

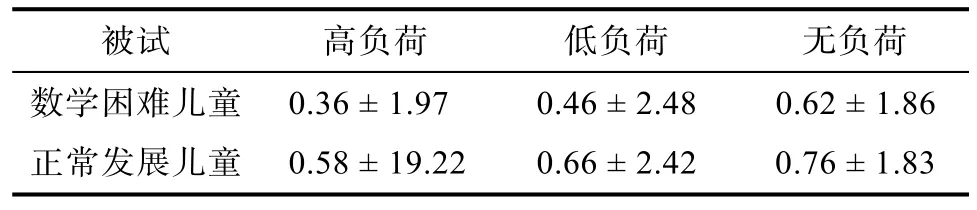
表3 最佳选择条件下各负荷情境中儿童的策略选择适应性正确率(M±SD)

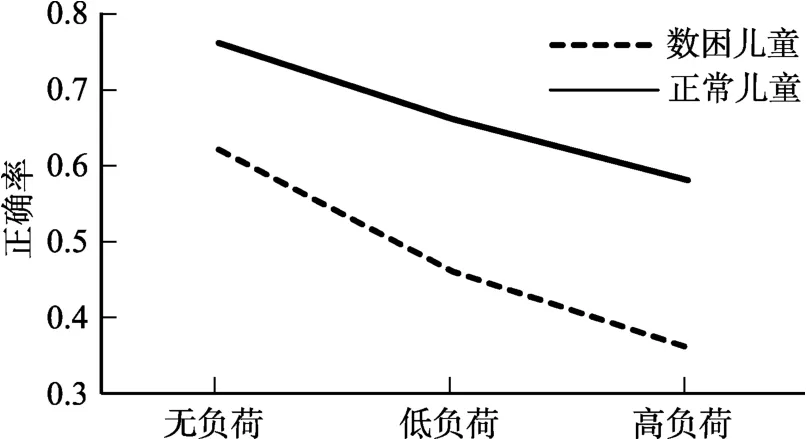
图6 实验条件与被试类型在策略选择性上的交互作用图

4 分析与讨论

本研究旨在考察中央执行负荷对数困儿童和正常儿童策略运用的差异性影响,揭示中央执行功能在数困儿童的策略运用中所发挥的独特作用。

4.1 数困儿童的估算策略执行

本研究发现,数困组儿童在无、低、高三种负荷条件下的正确率均差于正常组,而在无负荷和低负荷下的反应时也慢于正常组。这基本符合我们的预期及前人研究(Torbeyns et al.,2004b),相较于正常组,数困组中央执行功能较差,无法有效抑制额外或者不相关的干扰信息(Passolunghi,2011;吕娜,杨静,华晓腾,司继伟,王翔艳,2015),导致策略执行表现较差。但两组儿童的策略执行反应时在高负荷条件下差异并不显著。有研究发现,即使成年人也会受到负荷影响(司继伟等,2012),因此,正常组儿童的中央执行功能可能仍在发展,而高负荷任务太难,导致两个组均不能较好完成策略执行。而Δ分析也说明了这一点,在高负荷时,数困组正确率的Δ变小,但反应时的Δ却变大。虽然两组儿童反应时在高负荷条件下差异不显著,但数困组平均反应时还是长于正常组(3717 ms vs.3498 ms),Δ分析也发现,在正确率和反应时上,中央执行负荷会对数困组的策略执行产生独特影响,所以,整体来看,数困组的策略执行较差,这可能是由于数困组的中央执行功能较差所致。

数困儿童较差策略执行表现的深层原因可能是因为他们存在高水平的数学焦虑导致中央执行功能变差。尽管数困儿童在其它学科中的焦虑水平与正常儿童类似,却往往存在更高水平的数学焦虑,这可能导致中央执行功能较差,不能协调认知资源(Passolunghi,2011)。高数学焦虑导致较差数学表现,这可能是数困儿童同时会伴有更高水平数学焦虑的原因(Wahid,Yusof,&Razak,2014)。数学焦虑会占用一部分认知资源,导致数困儿童的认知资源从一开始就处于劣势,无负荷条件下数困组儿童较差的策略执行表现也印证了这一点。此外,随着年级升高,数学焦虑对策略运用的影响越来越突出,六年级受数学焦虑制约更多,表现为高焦虑儿童只顾及到速度而正确率较差(Si et al.,2016),这可能解释了数困组在高负荷条件下正确率低于正常组但反应时没有显著差异的原因。因此,我们推测数学焦虑导致数困儿童认知资源不足,从而间接导致较差策略执行,或者是直接因为认知资源不足所致。而成年人中高焦虑者的工作记忆负荷更高也印证了这一点(司继伟等,2014)。至于数学焦虑是如何导致数困儿童认知资源不足可能解释存在以下几点：加工效能理论(Eysenck,Derakshan,Santos,&Calvo,2007)认为,焦虑对认知加工效能的影响依赖于中央执行的抑制成分,负荷增加会导致中央执行抑制功能受损,从而导致焦虑个体更容易受到外部(分心物)或者内部(担心的想法)等无关刺激干扰,数困儿童有限的认知资源可能还会被调用一部分来抑制焦虑对主任务的干扰,而焦虑还会使有限的认知资源从估算任务(目标-导向注意系统)转移到焦虑情绪的注意(刺激-驱动注意系统) (Eysenck &Derakshan,2011),这些任务无关干扰都会与策略执行竞争有限的认知资源,使得本来就存在中央执行功能障碍的数困儿童的认知负荷更高,从而导致较差策略执行表现。此外,数学焦虑可能并不直接导致较差策略执行,而是通过中央执行功能作为(部分或完全)中介作用于策略执行(Si et al.,2016)。虽然正常组儿童的策略执行也会受负荷影响,但相比于同辈的数困组,正常组由于中央执行功能较正常,在策略执行整体上的表现也就更好,其负荷模式表现出稳定可预测的线性变化。而正常组在三种负荷上两两差异显著,这表明,本实验在负荷任务设置上具有良好区分度,从而保证了两组儿童是在同样实验条件下进行比较,结论可信度较高。总之,数困儿童的中央执行功能较差,导致较差的策略执行,且存在不同于正常组的中央执行负荷模式。

4.2 数困儿童的估算策略选择及适应性

在认知加工中,策略选择要比策略执行更为复杂,需要个体调用更多认知资源来协调主次任务(艾继如等,2016;Lemaire et al.,2004)。而本研究也显示,数困组中央执行功能较差,在策略选择反应时和正确率上均劣于正常组,中央执行负荷效应在两组儿童的策略选择正确率和反应时上差异均显著,Δ分析也发现,数困组的策略选择存在独特的负荷模式,且与其在策略执行上的反应时和正确率的变化模式也不一样。完成策略选择既需个体主动监控目标行为,抑制次任务的干扰,又要根据任务要求在不同策略之间灵活转换,协调运用认知资源(Lemaire &Lecacheur,2010),这都需要中央执行功能的参与。此外,相较于简单的策略执行,策略选择还存在一个策略判断过程,而数困儿童的中央执行功能可能较差,从而不能较好完成与策略选择有关的中央执行的抑制与转换功能,这可能导致中央执行负荷对策略选择的制约作用更大(艾继如等,2016),从而可能导致数困儿童在策略选择上的反应时和正确率的变化模式不同于策略执行。

在最佳选择条件下,被试要根据问题类型选择适应性策略,比较两种策略,选择一种适应性策略并抑制住另一策略。Ardiale和Lemaire (2013)曾指出,在选择策略时,认知系统会评估策略有效性并修正最初非最佳的选择而转向最佳策略,这些认知加工过程会消耗个体有限的认知资源。而数困儿童的中央执行功能较差,认知资源相对不足,当执行负荷任务时,没有足够认知资源评估策略,导致其在三种负荷下的策略选择适应性表现均显著差于正常组。但负荷与组别不存在显著交互作用。将本结果与对成人的策略适应性(司继伟等,2012)和用智力/年龄匹配设计研究刷新功能对数困儿童策略运用的影响(吕娜等,2015)的有关研究进行对比可发现,成人在双任务协调和正常儿童在记忆刷新条件下的策略适应性都会变差,即成人和表现最佳的年龄匹配组儿童的策略适应性也会受到负荷影响。据此推测,负荷增加时,任务难度也增加,两组儿童都更可能选择较简单的下调策略(吕娜等,2015),从而释放一部分认知资源,任务难度反而下降。而数困组策略适应性在三种负荷下均低于正常组,说明虽然负荷和组别均对个体的策略适应性产生影响,但负荷对两组儿童策略适应性的差异性影响低于个体在中央执行功能上的差异对结果的影响,这可能是存在显著组别差异和负荷条件差异却未出现交互作用的原因。此外,有研究表明,转换对策略适应性无显著影响,而刷新的影响显著(华晓腾,2013),而本研究可能主要涉及中央执行的转换功能,这可能也是未出现交互作用的原因。但整体来说,数困组策略选择适应性还是显著差于正常组。数困儿童中央执行功能较差,而策略运用与中央执行的转换和抑制功能关系密切。对此,Lemaire和Lecacheur (2010)曾提出策略启动程序,认为个体从一个试次转换到另一个时,刚执行过的策略仍处于较高激活状态,更容易获得和回忆,个体会更倾向于重复相同的策略。但当任务要求选择最佳策略时,正常组会协调认知资源来抑制重复同一策略的反应倾向,而数困组中央执行抑制功能较差,不能在当前问题上适应性地选择最佳策略,从而导致较差的策略选择适应性。另一可能解释是策略集的重构过程(Lemaire &Lecacheur,2010)。一旦用某一策略解决了某一问题,个体必须重构认知系统,这一过程涉及一系列的中央执行抑制和转换过程,个体必须抛弃旧策略或抑制无关策略的激活,使用工作记忆中可获得的或激活相关的策略来作为将要执行的策略。这两种假设可能分别或共同解释了较差中央执行功能的数困儿童的较差策略选择适应性的内在原因。Lemaire和Lecacheur (2011)曾证实,中央执行抑制功能影响策略选择,抑制功能越高的儿童策略选择适应性越好。这也佐证了本研究结果。

此外,估算策略选择适应性可能存在着跨文化差异,与其它文化背景的人相比,中国被试虽然策略执行更快更精确,但适应性较差,尤其是存在认知负荷时,这可能是因为中国学校教育高度重视的数学练习与训练虽然导致高度自动化解题,却反而降低了适应性,而欧洲和北美教育所强调的灵活性和探索性反而增加了适应性(Imbo &LeFevre,2009)。中国被试更加不能容忍这种近似解题策略,当要求估算时,他们可能不得不抑制精确计算倾向(Imbo &LeFevre,2011),这加重了数困儿童的认知负荷。这些都将导致被试(包括正常组)没有在所有题目上选择最佳策略。

总之在策略选择及适应性上,虽然两组儿童都会受到负荷影响,但数困组的表现更差,这与其中央执行功能较差不无关系。之前有研究表明,数困儿童较差的策略运用既有发展缺陷(吕娜等,2015),也有发展延迟(华晓腾,2013),但本研究并不能得出确切结论,需要在未来研究中采用智力/年龄匹配设计继续探讨。但就数困儿童的中央执行功能较差而言,本研究和前人一致(Passolunghi,2011)。那么能否通过训练来提高其中央执行功能呢？有证据显示,抑制训练已被广泛应用于儿童和成人的认知能力训练中(Manuel,Bernasconi,&Spierer,2013),可明显提高数困儿童的抑制能力(刘翠珍,2013),也能有效提升其策略运用成绩,尤其是在负荷条件和复杂策略下(Bergman-Nutley &Klingberg,2014)。因此,未来从中央执行功能可塑性角度开展训练工作,将有助于深入理解本研究中数困儿童策略运用的中央执行负荷效应的理论基础,以及为制定出有效提高数困儿童策略运用的干预方案提供科学依据。

5 结论

基于上述结果与分析,可得到如下结论：

(1)在无、低和高三种负荷条件下,数困组儿童的估算策略执行和策略选择普遍差于正常组儿童,但二者在无负荷条件下的策略表现都比有负荷的更好;

(2)无论是数困组还是正常组儿童,其策略执行和选择都会随中央执行负荷的增加而变差,但数困组受到负荷的影响更大,且负荷变化模式与正常组不同;

(3)在不同中央执行负荷条件下,数困组儿童的策略选择适应性都较正常组差,随着负荷的升高,两组儿童的策略选择适应性都显著降低。

Ai,J.R.,Zhang,H.D.,Si,J.W.,Lu,C.,&Zhang,T.Z.(2016).The effects of presenting mode,reaction order of dual task on adults’ arithmetic strategy choice and execution.Acta Psychologica Sinica,48(10),1248–1257.

[艾继如,张红段,司继伟,卢淳,张堂正.(2016).任务呈现方式、双任务反应顺序影响算术估算策略选择与执行.心理学报,48(10),1248–1257.]

Ardiale,E.,&Lemaire,P.(2013).Within-item strategy switching in arithmetic: A comparative study in children.Frontiers in Psychology,4,924.

Bergman-Nutley,S.,&Klingberg,T.(2014).Effect of working memory training on working memory,arithmetic and following instructions.Psychological Research,78(6),869–877.

Cheng,J.P.,Luo,Y.J.,&Cui,F.(2017).Empathy for pain influenced by cognitive load: Evidence from an ERP study.Acta Psychologica Sinica,49(5),622–630.

[程家萍,罗跃嘉,崔芳.(2017).认知负荷对疼痛共情的影响: 来自ERP研究的证据.心理学报,49(5),622–630.]

Desoete,A.,&De Weerdt,F.(2013).Can executive functions help to understand children with mathematical learning disorders and to improve instruction?.Learning Disabilities,11(2),27–39.

Ding,X.,Lv,N.,Yang,Y.L.,&Si,J.W.(2017).Age-related differences of different components of working memory:The predictive effect on strategy utilization in arithmetic.Acta Psychologica Sinica,49(6),759–770.

[丁晓,吕娜,杨雅琳,司继伟.(2017).工作记忆成分的年龄相关差异对算术策略运用的预测效应.心理学报,49(6),759–770.]

Eysenck,M.W.,&Derakshan,N.(2011).New perspectives in attentional control theory.Personality &Individual Differences,50(7),955–960.

Eysenck,M.W.,Derakshan,N.,Santos,R.,&Calvo,M.G.(2007).Anxiety and cognitive performance: Attentional control theory.Emotion,7(2),336–353.

Fletcher,J.M.,Stuebing,K.K.,Morris,R.D.,&Lyon,G.R.(2013).Classification and definition of learning disabilities.In H.L.Swanson,K.R.Harris,&S.Graham (Eds.),Handbook of learning disabilities (pp.33–50).New York: Guilford.

Geary,D.C.(2004).Mathematics and learning disabilities.Journal of Learning Disabilities,37(1),4–15.

Han,S.H.,&Kim,M.S.(2004).Visual search does not remain efficient when executive working memory is working.Psychological Science,15(9),623–628.

Hinault,T.,Dufau,S.,&Lemaire,P.(2014).Sequential modulations of poorer-strategy effects during strategy execution: An event-related potential study in arithmetic.Brain &Cognition,91,123–130.

Hinault,T.,Lemaire,P.,&Phillips,N.(2016).Aging and sequential modulations of poorer strategy effects: An EEG study in arithmetic problem solving.Brain Research,1630,144–158.

Hinault,T.,Lemaire,P.,&Touron,D.(2017).Aging effects in sequential modulations of poorer-strategy effects during execution of memory strategies.Memory,25(2),176–186.

Hua,X.T.(2013).The effect of shifting/updating executive function on mathematics learning disabilities children's strategy use in computational estimation (Unpublished master’s thesis).Shandong Normal University,Ji’nan.

[华晓腾.(2013).转换/刷新执行功能对数学困难儿童算术估计策略运用的影响 (硕士学位论文).山东师范大学,济南.]

Hua,X.T.,Si,J.W.,&Lu,C.(2012).Mathematical estimation capacities of children with mathematics learning disabilities.Advances in Psychological Science,20(10),1633–1641.

[华晓腾,司继伟,卢淳.(2012).数学困难儿童的数学估计能力.心理科学进展,20(10),1633–1641.]

Huang,B.J.,Feng,H.M.,Si,J.W.,Zhang,J.,&Wang,X.Y.(2016).Dual-task coordination and task presentation mode influence arithmetic strategy execution in adults: Evidence from computational estimation.Acta Psychologica Sinica,48(6),671–683.

[黄碧娟,封洪敏,司继伟,张杰,王翔艳.(2016).双任务协调、任务呈现方式影响成人算术策略执行: 估算证据.心理学报,48(6),671–683.]

Huang,D.Q.,&Chen,Y.H.(2016).Study on the development of math cognitive abilities for mathematic difficulties in grade 2～6 primary students.Journal of Mathematics Education,25(2),70–74.

[黄大庆,陈英和.(2016).小学二至六年级数学困难儿童数学认知能力的发展.数学教育学报,25(2),70–74.]

Imbo,I.,Duverne,S.,&Lemaire,P.(2007).Working memory,strategy execution,and strategy selection in mental arithmetic.Quarterly Journal of Experimental Psychology,60(9),1246–1264.

Imbo,I.,&LeFevre,J.A.(2009).Cultural differences in complex addition: Efficient Chinese versus adaptive Belgians and Canadians.Journal of Experimental Psychology: Learning,Memory,&Cognition,35(6),1465–1476.

Imbo,I.,&LeFevre,J.A.(2011).Cultural differences in strategic behavior: A study in computational estimation.Journal of Experimental Psychology: Learning,Memory,&Cognition,37(5),1294–1301.

Imbo,I.,Vandierendonck,A.,&Rosseel,Y.(2007).The influence of problem features and individual differences on strategic performance in simple arithmetic.Memory &Cognition,35(3),454–463.

Lemaire,P.,Arnaud,L.,&Lecacheur,M.(2004).Adults'age-related differences in adaptivity of strategy choices:Evidence from computational estimation.Psychology and Aging,19(3),467–481.

Lemaire,P.,&Calliès,S.(2009).Children's strategies in complex arithmetic.Journal of Experimental Child Psychology,103(1),49–65.

Lemaire,P.,&Lecacheur,M.(2010).Strategy switch costs in arithmetic problem solving.Memory &Cognition,38(3),322–332.

Lemaire,P.,&Lecacheur,M.(2011).Age-related changes in children's executive functions and strategy selection: A study in computational estimation.Cognitive Development,26(3),282–294.

Lemaire,P.,Lecacheur,M.,&Farioli,F.(2000).Children's strategy use in computational estimation.Canadian Journal of Experimental Psychology,54(2),141–148.

Li,H.X.,Si,J.W.,Chen,Z.J.,&Zhang,T.Z.(2015).Approximate number system in human.Advances in Psychological Science,23(4),562–570.

[李红霞,司继伟,陈泽建,张堂正.(2015).人类的近似数量系统.心理科学进展,23(4),562–570.]

Liu,C.(2004).Working memory and processing speed in children with arithmetical difficulties.Journal of Nanjing Normal University (Social Science Edition),(3),81–88.

[刘昌.(2004).数学学习困难儿童的认知加工机制研究.南京师范大学学报(社会科学版),(3),81–88.]

Liu,C.Z.(2013).Working memory training research of mathematical learning difficulty students (Unpublished master’s thesis).Inner Mongolia Normal University.

[刘翠珍.(2013).数学学习困难学生的工作记忆训练研究(硕士学位论文).内蒙古师范大学.]

Lv,N.,Yang,J.,Hua,X.T.,Si,J.W.,&Wang,X.Y.(2015).Memory updating affects MD children’s arithmetic strategy use: Evidences from the chronological age/intelligencematched design.Studies of Psychology and Behavior,13(6),784–793.

[吕娜,杨静,华晓腾,司继伟,王翔艳.(2015).记忆刷新影响数困儿童的算术策略运用: 来自年龄/智力匹配设计的证据.心理与行为研究,13(6),784–793.]

Manuel,A.L.,Bernasconi,F.,&Spierer,L.(2013).Plastic modifications within inhibitory control networks induced by practicing a stop-signal task: An electrical neuroimaging study.Cortex,49(4),1141–1147.

Mata,R.,Josef,A.K.,&Lemaire,P.(2015).Chapter 6-Adaptive decision making and aging.In T.M.Hess,J.Strough,&C.Lckenhoff (Eds.),Aging and decision making: Empirical and applied perspectives (pp.105–122).New York: Academic Press.

Passolunghi,M.C.(2011).Cognitive and emotional factors in children with mathematical learning disabilities.International Journal of Disability,Development and Education,58(1),61–73.

Passolunghi,M.C.,&Siegel,L.S.(2004).Working memory and access to numerical information in children with disability in mathematics.Journal of Experimental Child Psychology,88(4),348–367.

Si,J.,Li,H.,Sun,Y.,Xu,Y.,&Sun,Y.(2016).Age-related differences of individuals’ arithmetic strategy utilization with different level of math anxiety.Frontiers in Psychology,7,1612.

Si,J.W.,Liu,Y.Q.,Jia,G.J.,&Huang,B.J.(2016).The central executive load and the individual’s strategy use adaptability with cognitive style: Behavioral and eye-tracking evidence.Journal of Soochow University (Educational Science Edition),4(1),85–95.

[司继伟,刘亚琼,贾国敬,黄碧娟.(2016).认知风格、中央执行负荷影响算术估算的策略选择适应性: 行为与眼动证据.苏州大学学报(教育科学版),4(1),85–95.]

Si,J.W.,Xu,Y.L.,Feng,H.M.,Xu,X.H.,&Zhou,C.(2014).Differences of arithmetic strategy use in adults with different math anxieties: An ERP study.Acta Psychologica Sinica,46(12),1835–1849.

[司继伟,徐艳丽,封洪敏,许晓华,周超.(2014).不同数学焦虑成人的算术策略运用差异: ERP研究.心理学报,46(12),1835–1849.]

Si,J.W.,Yang,J.,Jia,G.J.,&Zhou,C.(2012).The effect of central executive load on adult’s strategy using in computational estimation.Acta Psychologica Sinica,44(11),1490–1500.

[司继伟,杨佳,贾国敬,周超.(2012).中央执行负荷对成人估算策略运用的影响.心理学报,44(11),1490–1500.]

Torbeyns,J.,Verschaffel,L.,&Ghesquière,P.(2004a).Strategy development in children with mathematical disabilities.Journal of Learning Disabilities,37(2),119–131.

Torbeyns,J.,Verschaffel,L.,&Ghesquière,P.(2004b).Strategic aspects of simple addition and subtraction: The influence of mathematical ability.Learning &Instruction,14(2),177–195.

Uittenhove,K.,&Lemaire,P.(2012).Sequential difficulty effects during strategy execution: A study in arithmetic.Experimental Psychology,59(5),295–301.

Wahid,S.N.S.,Yusof,Y.,&Razak,M.R.(2014).Math anxiety among students in higher education level.Procedia–Social and Behavioral Sciences,123,232–237.

Wang,M.Y.,&Chen,Y.H.(2006).The influence of central executive of working memory on children’s arithmetical cognitive strategies.Psychological Development and Education,22(4),24–28.

[王明怡,陈英和.(2006).工作记忆中央执行对儿童算术认知策略的影响.心理发展与教育,22(4),24–28.]

Xu,C.,Wells,E.,Lefevre,J.A.,&Imbo,I.(2014).Strategic flexibility in computational estimation for Chinese- and Canadian-educated adults.Journal of Experimental Psychology:Learning,Memory,&Cognition,40(5),1481–1497.

Zhang,S.D.,&Dong,Q.(2012).On the relationship between number processing or dyscalculia and working memory.Chinese Journal of Special Education,(2),40–47.

[张树东,董奇.(2012).数字加工和计算障碍与工作记忆的关系研究.中国特殊教育,(2),40–47.]