含虚拟同步发电机的多端柔性直流系统稳定性分析

付 强, 杜文娟, 黄登一, 王海风

(新能源电力系统国家重点实验室(华北电力大学), 北京市102206)

0 引言

近年来,随着可再生能源的大力开发和新能源电力系统的快速发展[1],以矢量控制为代表的电压源型换流器(VSC)得到了广泛应用[2-3],由其构成的柔性直流输电系统成为了解决远距离电能传输的有效方案[4]。但是,矢量控制的VSC不具有旋转惯性[5],易引入谐波[6],无法为交流系统提供必要的电压和频率支撑,降低了电网运行的稳定性[7]。为此,模拟同步发电机的运行特性,提出了虚拟同步发电机(virtual synchronous generator,VSG)控制,增加了系统惯性,提供了电压和频率支撑[8-11],引起了众多学者的广泛关注。

目前针对VSG的稳定性研究主要集中在两个方面:一方面是针对单个VSG控制的VSC进行研究,另一个方面是针对含VSG的多端直流系统进行研究。在第一个方面,常假设直流系统为恒定功率源或直流电压源,系统的复杂度较低,提出了相关的稳定性控制方法。例如文献[12]通过结合传统无惯性下垂控制和VSG控制的优势,提出了基于VSG的下垂控制;文献[13]设计了新的解耦控制算法,实现了VSG有功和无功功率的独立输出;文献[14]研究了解耦控制算法的参数设计,提出了考虑系统稳定性裕量的参数设计方案。

在VSG接入对交流系统稳定性影响的研究方面,主要采用模式分析法和频域分析法。例如文献[15]采用模式分析法分析了控制参数对交流系统稳定性的影响,提出了控制参数的优化方案。文献[16]采用频域分析法分析了VSG控制与发电机间产生的谐振现象,提出了基于一阶控制环节的解决措施。文献[17]提出了一种新的阻尼控制方法,采用实验验证了其能够有效提升低频振荡的稳定性。

在第二个方面,考虑到系统的复杂度进一步上升,采用的主要稳定性分析方法为模式分析法。例如文献[18]针对传统VSG控制策略难以响应直流系统注入功率变化的现象,提出了具有限幅环节的VSG直流电压下垂控制方式。文献[19]从物理机理的角度出发,设计了基于虚拟调速器的VSG下垂控制策略,并采用模式分析法研究了其对交流系统稳定性的影响。

综上,可以得出目前针对含VSG的多端柔性直流系统稳定性研究主要存在以下问题。

1)虽然针对含VSG的多端直流系统的控制策略已经被提出,但是其稳定性建模及其机理研究暂未展开。

2)目前的研究忽略了直流系统自身的动态过程[18-19]。当VSG采用直流电压下垂控制后,多端直流系统中将出现新的振荡模式,原有的快速响应特性可能会消失。故对于采用直流电压下垂控制的VSG来讲,将直流系统等效为恒定功率源进行分析是具有一定局限性的,没有考虑到直流系统自身的稳定性问题。

本文针对上述问题,首先建立了矢量控制和VSG控制下VSC的传递函数模型,形成了多端直流系统的闭环互联模型;然后,采用阻尼转矩分析法研究了VSG接入对直流系统稳定性的影响,得出了当直流系统中存在多个VSG时,VSG间可能会发生强交互现象,导致模式排斥,进而引起直流系统的振荡;最后,对一个三端直流系统进行了时域仿真分析,验证了上述研究结果,并给出了能够提升直流系统稳定性的VSG参数调节方法。

1 不同控制下VSC的传递函数模型

图1所示为N端柔性直流系统中第j个VSC(j=1,2,…,N,下同)接入交流系统的示意图,其中Xj为第j个VSC与交流系统连接线路上的电抗,Vpcc,j为第j个VSC与交流系统连接点处的节点电压,假定其相角为0,Vac,j∠θac,j为第j个VSC输出的交流电压幅值及其相角,Id,j+jIq,j为第j个VSC交流侧线路上的电流,Pj+jQj为第j个VSC注入交流系统的有功和无功功率,Rdc,j和Xdc,j分别为第j个VSC直流侧的电阻和电抗,Cj和Vdc,j分别为第j个VSC直流侧的电容及其直流电压,Idc,j和Ij,dc分别为第j个VSC直流侧电容的输入和输出电流。

图1 VSC接入交流系统的示意图Fig.1 Schematic diagram of AC power system with VSC

以第j个VSC直流侧电容的输入电流Idc,j为输入信号,以第j个VSC直流侧电容的直流电压Vdc,j为输出信号,可得出在不同控制下,第j个VSC对于直流系统的传递函数模型Zj(s)。本文以VSG控制和矢量控制为例,建模如下。

1.1 定直流电压控制下VSC的传递函数模型

如附录A图A1所示为第j个VSC在定直流电压控制下的控制框图,其中有功环采用定直流电压控制方式[20],KP，dc,j和KI，dc,j分别为有功外环的比例系数和积分系数;无功外环采用定无功功率控制方式,KP，q,j和KI，q,j分别为无功外环的比例系数和积分系数。内环采用电流解耦控制,KP，i,d,j，KI，i,d,j和KP，i,q,j，KI，i,q,j分别为有功电流内环和无功电流内环的比例和积分系数。Tv为一阶延时环节的时间常数,用于模拟调制环节的时滞,Vac,d,j和Vac,q,j分别为节点电压Vac,j的d轴和q轴分量。

由附录A图A1可得:

(1)

考虑到交直流连接线路上的动态方程满足:

(2)

式中：ω0为电网基值频率。

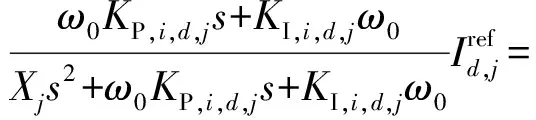
(3)

联立式(1)和式(3)可得:

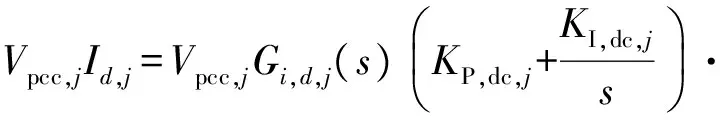
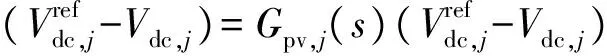
(4)

考虑到直流侧电容上的动态方程,有

(5)

由式(5)可得第j个VSC的传递函数模型为:

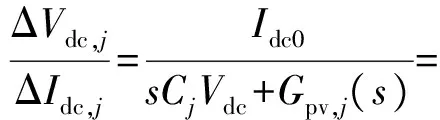
(6)

式中:下标“0”表示状态变量的稳态值。

1.2 直流电压下垂控制下VSC的传递函数模型

附录A图A2所示为第j个VSC在直流电压下垂控制下的控制框图,其中有功环采用直流电压下垂控制方式[21],Kdc,j为直流电压下垂系数,KP,p,j和KI,p,j为下垂控制外环的比例和积分系数,剩余控制参数与附录A图A1中一致。

由附录A图A2可得:

(7)

忽略附录A图A2中的时滞环节[2],联立式(7)和式(3)可得:

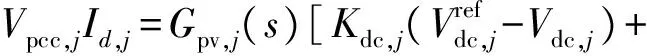
(8)

求解式(8)可得:

(9)

将式(9)代入式(5)可得第j个VSC的传递函数模型为:

(10)

1.3 VSG控制下VSC的传递函数模型

由附录A图A3可得:

(11)

考虑到VSG与交流系统的连接线路,有如下表达式[23]:

(12)

考虑到附录A图A4中VSG有功功率和无功功率的耦合关系,可得:

(13)

令GK,j=GK,j(λj),λj为第j个VSC的振荡模式,由附录A图A3可得,VSG的二阶虚拟转子运动方程为:

(14)

考虑到如式(5)所示的直流侧动态方程,可得第j个VSG控制的VSC的传递函数模型为:

(15)

2 VSG接入对多端柔性直流系统稳定性的影响

2.1 阻尼转矩分析

阻尼转矩分析法的依据是经典控制理论和发电机转子运动所受力矩的分解。按照阻尼转矩法的基本思想,发电机剩余部分对发电机转子运动的转矩贡献可分解为两部分:一部分是阻尼转矩,决定转子运动振荡的阻尼,即发电机输出功率低频振荡的阻尼;另一部分是同步转矩,决定发电机的同步能力,影响的是发电机输出功率的振荡频率。阻尼转矩的物理意义是:与角速度成正比的力矩,是角位移的制动力,起到了阻尼的作用。如果发电机剩余部分对转子运动的阻尼转矩是负的,则会降低发电机本身的稳定性,当其提供的负阻尼大于转子运动自身的正阻尼时,将导致系统发散失稳;如果发电机剩余部分对转子运动的阻尼转矩是正的,转子运动振荡的阻尼会得到提升,其稳定性也会随之改善[23]。

考虑到虚拟同步控制中,二阶虚拟转子的运动方程与发电机类似,所以本文采用阻尼转矩分析法分析系统中其他环节对VSG稳定性的影响。

对于一个含VSG的N端柔性直流系统,总可以简化为如图2所示的传递函数示意图,其中传递函数Z(s)可由式(6)、式(10)和式(15)求得。不失一般性,假设第1个VSC采用VSG控制,采用阻尼转矩分析法研究其余VSC对第1个VSC提供的阻尼转矩。

图2 N端柔性直流系统的传递函数Fig.2 Transfer function of N-terminal flexible DC system

图2中,有

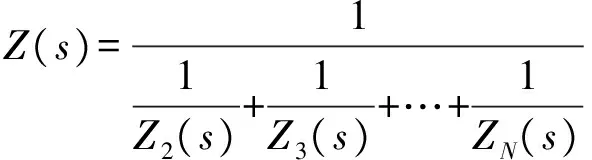
(16)

式(14)的二阶方程可写为:

(17)

其中,ΔPT可按式(18)分解。

ΔPT=TdsΔP1+TgΔP1

(18)

将式(18)代入式(17)可得:

(19)

从式(19)可以看出,VSG控制的VSC自身的振荡阻尼受到两部分因素的影响,其中一部分是自身控制参数D1/(2H1)提供的阻尼,另一部分则是外部直流系统提供的阻尼-Td/(2H1)。一般来讲,VSG控制参数中均有D1/(2H1)>0,所以含VSG的多端直流系统是否稳定取决于外部直流系统对VSG控制的VSC提供的阻尼大小,其稳定性判据为:当D1-Td>0,系统稳定。

由图2可知,外部直流系统的反馈传递函数为:

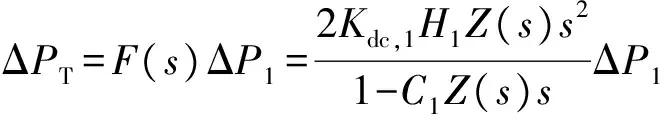
(20)

假设VSG控制的振荡模式为λ1=ε1+jω1,则对于λ1,在复频域有如下方程成立:

ΔPT=F1(λ1)ΔP1=Tdλ1ΔPj+TgΔPj=

Td(ε1+jω1)ΔPj+TgΔPj=

(Tdε1+Tg+jTdω1)ΔPj

(21)

由式(21)可解得:

(22)

依据式(22),可计算剩余直流系统F(s)给VSG控制的VSC提供的阻尼-Td/(2H1),进而判定VSG接入后,多端直流系统的稳定性。综上,也可得出提升直流系统中振荡模式阻尼的方法有:减小惯性系数H1,增加阻尼系数D1和增大下垂系数Kdc,1。

2.2 模式排斥

当N端柔性直流系统中含有多个VSG控制的VSC时,F(s)中必然含有其他振荡模式,令其中一个为λz,由式(22)可知,当λz=λ1时,Td→∞,即外部直流系统将向VSG控制的VSC提供一个非常大的阻尼,这将很可能导致直流系统失稳,证明如下。

考虑到λ1是H(s)的开环振荡模式,λz是F(s)的开环振荡模式,则有式(23)成立。

(23)

由图2可得H(s)F(s)=1,将式(23)代入,有

(s-λ1)(s-λz)h(s)z(s)=1

(24)

(25)

式(25)说明,当一个VSG控制的VSC的H(s)的开环模式λ1与剩余直流系统F(s)的开环模式λz接近时,多端直流系统的闭环模式将发生互相排斥的现象,导致其中一个模式的阻尼变差,严重的将引起直流系统内的振荡现象。

考虑到矢量控制的频率较高,所以上述模式排斥现象是由于VSG控制与VSG控制间的动态交互引起的,这再次验证了当多个VSG接入同一多端直流系统中时,直流系统的动态特性将发生改变,其内部的动态过程将不能忽略,并存在稳定性问题。

3 仿真验证

3.1 系统介绍

如图3所示为一个三端柔性直流系统,其中VSC-1采用定直流电压矢量控制方式,向直流系统注入有功功率,VSC-2采用直流电压下垂矢量控制方式,VSC-3采用VSG控制方式。VSC-2和VSC-3输出有功功率,系统参数见附录A表A1。

图3 三端柔性直流输电系统Fig.3 Three-terminal flexible DC system

3.2 含单个VSG的直流系统稳定性分析

单个VSG对直流系统稳定性的影响主要体现在其主导模式的阻尼特性上,如果阻尼为正,则系统稳定,反之系统失稳。本小节针对其3个控制参数,研究不同控制参数对其振荡模式阻尼的影响效果,并给出合理的参数选择建议。

3.2.1惯性系数对VSG振荡模式阻尼的影响

由附录A图A5可知,惯性系数增大会降低VSG振荡模式的阻尼,并趋近于0,但是不会导致失稳,这一结论与式(19)的分析一致,验证了阻尼转矩分析的正确性。进一步地,采用MATLAB软件(下同)对附录A图A5中的结果进行了时域仿真验证,如附录A图A6所示。

附录A图A6中,系统在0.1 s于VSC-1处发生了20%的功率波动,并于0.2 s时消除。由附录A图A6可知,含VSG的多端直流系统中出现了低频的功率振荡,当惯性系数较小时,振荡可以较快平息,当惯性系数增大时,振荡的波动时间将增加,平息时间延长。所以,在其他参数不变的条件下,应尽可能降低VSG的惯性系数,以提升直流系统中振荡模式的阻尼。

3.2.2阻尼系数对VSG振荡模式阻尼的影响

由附录A图A7可知,增大阻尼系数会提升VSG振荡模式的阻尼,当外部直流系统提供的阻尼转矩较小时,近似呈现线性增长,这一结论与式(19)的分析一致。类似的,对附录A图A7中的结果进行了时域仿真验证,如附录A图A8所示。

3.2.3VSG直流电压下垂系数对振荡模式阻尼的影响

由附录A图A9可知,增大下垂系数会提升VSG振荡模式的阻尼,改善直流系统的稳定性。结合式(22)可知,下垂系数Kdc,3与转矩Td成正比,增加下垂系数相当于增加转矩Td。类似的,对附录A图A9中的结果进行了时域仿真验证,如附录A图A10所示。

3.3 含多个VSG的直流系统稳定性分析

如2.2节所述,当直流系统VSC-2和VSC-3同时采用VSG控制时,应该调节参数使得新接入VSG的开环模式与直流系统中原有的开环模式远离,否则多个振荡模式间可能会发生模式排斥现象,引起直流系统的稳定性问题,验证如下。

首先,按照2.2节所述计算图3中VSC-2的开环振荡模式和剩余直流系统的开环振荡模式,如附录A表A2所示,可见VSC-2与剩余直流系统的开环振荡模式接近,此时,将VSC-2并入直流系统,求得直流系统的闭环模式如附录A表A2第3行所示,发现模式发生了排斥,导致了VSC-2振荡模式失稳,验证了理论分析的正确性。

图4 模式排斥的消除Fig.4 Elimination of modal exclusion

最后,对图4中的结果进行了时域仿真,验证了上述结论和分析的正确性,如图5所示。

图5 不同控制参数下柔性直流系统的时域仿真结果Fig.5 Time-domain simulation results of VSC-HVDC system with different control parameters

由图5可得,当新接入VSG的开环模式与原系统中存在的开环模式接近时,将发生模式排斥现象,导致直流系统产生振荡,威胁直流系统的稳定性。随着接入VSG的VSC的增多,直流系统的动态特性值得进一步研究,很有可能影响到交流系统的稳定性,而不能进行简单的理想化等效。对于模式排斥现象,可以通过调节参数的方式解决,使得接入VSG的开环模式与原有模式远离,维持系统稳定性。

4 结论

本文针对含VSG的多端柔性直流系统,建立了矢量控制和VSG控制下VSC的传递函数模型,采用阻尼转矩分析法研究了VSG接入对多端直流系统稳定性的影响,得出如下结论。

1)VSG的接入改变了原有多端直流系统的动态特性,且存在一定的稳定性问题。在研究VSG控制对交流系统稳定性的影响前,应先确保直流系统内部的稳定,将直流系统简单地等效为恒功率源这一假设具有一定的分析局限性。

2)VSG接入直流系统后,引入了新的振荡模式,为避免直流系统内部产生振荡现象,可通过减小惯性系数,增加阻尼系数和增大下垂系数来提升直流系统振荡的阻尼。

3)多个VSG接入直流系统后,VSG控制之间将会通过直流系统产生动态交互,当VSG控制的开环模式与原直流系统的开环模式接近,将有可能发生模式排斥现象,导致直流系统失稳。

4)多个VSG间的模式排斥现象可通过设定合理的参数避免,以维持直流系统的稳定性,而VSG控制对交流系统稳定性的影响应该建立在上述基础之上。

本文的研究过程及其结论主要建立在一个理想的直流系统中,并未考虑交流系统动态过程的影响,未来的研究内容将以本文的成果为基础,进一步考虑交流系统的动态过程,以期能够得出VSG对交直流混联电力系统的影响规律及其内在机理,进而对VSG在复杂电力系统中的稳定运行提供理论支撑。

感谢华北电力大学中央高校基本科研业务费青年培养项目(JB2017108)的资助。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 李程昊,詹鹏,文劲宇,等.适用于大规模风电并网的多端柔性直流输电系统控制策略[J].电力系统自动化,2015,39(11):1-7.DOI:10.7500/AEPS20140717010.

LI Chenghao, ZHAN Peng, WEN Jinyu, et al. A multi-terminal VSC-HVDC system control strategy for large wind farms integration[J]. Automation of Electric Power Systems, 2015, 39(11): 1-7. DOI: 10.7500/AEPS20140717010.

[2] 徐峥.柔性直流输电系统[M].北京:机械工业出版社,2014.

[3] 汤广福.基于电压源换流器的高压直流输电系统[M].北京:中国电力出版社,2010.

[4] 王成山,罗凤章,张天宇,等.城市电网智能化关键技术[J].高电压技术,2016,42(7):2017-2027.

WANG Chengshan, LUO Fengzhang, ZHANG Tianyu, et al. Review on key technologies of smart urban power network[J]. High Voltage Engineering, 2016, 42(7): 2017-2027.

[5] 程冲,杨欢,曾正,等.虚拟同步发电机的转子惯量自适应控制方法[J].电力系统自动化,2015,39(19):82-89.DOI:10.7500/AEPS20141130003.

CHENG Chong, YANG Huan, ZENG Zheng, et al. Rotor inertia adaptive control method of VSG[J]. Automation of Electric Power Systems, 2015, 39(19): 82-89. DOI: 10.7500/AEPS20141130003.

[6] 徐海珍,张兴,刘芳,等.基于微分补偿环节虚拟惯性的虚拟同步发电机控制策略[J].电力系统自动化,2017,41(3):96-102.DOI:10.7500/AEPS20160420001.

XU Haizhen, ZHANG Xing, LIU Fang, et al. Control strategy of virtual synchronous generator based on differential compensation virtual inertia [J]. Automation of Electric Power Systems, 2017, 41(3): 96-102. DOI: 10.7500/AEPS20160420001.

[7] 郑天文,陈来军,陈天一,等.虚拟同步发电机技术及展望[J].电力系统自动化,2015,39(21):165-175.DOI:10.7500/AEPS20150508006.

ZHENG Tianwen, CHEN Laijun, CHEN Tianyi, et al. Review and prospect of virtual synchronous generator technologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-175. DOI: 10.7500/AEPS20150508006.

[8] 赵杨阳,柴建云,孙旭东.基于虚拟同步发电机的柔性虚拟调速器模型[J].电力系统自动化,2016,40(10):8-15.DOI:10.7500/AEPS20150728014.

ZHAO Yangyang, CHAI Jianyun, SUN Xudong. Flexible virtual governor model based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2016, 40(10): 8-15. DOI: 10.7500/AEPS20150728014.

[9] 王金华.虚拟同步发电机的同步频率谐振机理和阻尼抑制[D].杭州:浙江大学,2016.

[10] 徐海珍,张兴,刘芳,等.基于超前滞后环节虚拟惯性的VSG控制策略[J].中国电机工程学报,2017,37(7):1918-1927.

XU Haizhen, ZHANG Xing, LIU Fang, et al. Virtual synchronous generator control strategy based on lead-lag link virtual inertia[J]. Proceedings of the CSEE, 2017, 37(7): 1918-1927.

[11] 黄林彬,章雷其,辛焕海,等.下垂控制逆变器的虚拟功角稳定机理分析[J].电力系统自动化,2016,40(12):117-123.DOI:10.7500/AEPS20150709007.

HUANG Linbin, ZHANG Leiqi, XIN Huanhai, et al. Mechanism analysis of virtual power angle stability in droop controlled inverters[J]. Automation of Electric Power Systems, 2016, 40(12): 117-123. DOI: 10.7500/AEPS20150709007.

[12] LIU J, MIURA Y, ISE T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3600-3611.

[13] LI B, ZHOU L, YU X, et al. Improved power decoupling control strategy based on virtual synchronous generator[J]. IET Power Electronics, 2017, 10(4): 462-470.

[14] WU Heng, RUAN Xinbo, YANG Dongsheng, et al. Small-signal modeling and parameters design for virtual synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4292-4303.

[15] 张玉治,张辉,贺大为,等.具有同步发电机特性的微电网逆变器控制[J].电工技术学报,2014,29(7):261-268.

ZHANG Yuzhi, ZHANG Hui, HE Dawei, et al. Control strategy of micro grid converters with synchronous generator characteristic[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 261-268.

[16] HIRASE Y, SUGIMOTO K, SAKIMOTO K, et al. Analysis of resonance in microgrids and effects of system frequency stabilization using a virtual synchronous generator[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1287-1298.

[17] SHINTAI T, MIURA Y, ISE T. Oscillation damping of a distributed generator using a virtual synchronous generator[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 668-676.

[18] MEI S, ZHENG T, CHEN L, et al. A comprehensive consensus-based distributed control strategy for grid-connected PV-VSG[C]// 35th Chinese Control Conference (CCC), July 27-29, 2016, Chengdu, China.

[19] 王炜宇,李勇,曹一家,等.基于虚拟调速器的MTDC虚拟同步机控制策略[J/OL].中国电机工程学报[2017-09-16].https://doi.org/10.13334/j.0258-8013.pcsee.170614.

WANG Weiyu, LI Yong, CAO Yijia, et al. The virtual synchronous generator technology based on virtual governor for MTDC system[J]. Proceedings of the CSEE[2017-09-16]. https://doi.org/10.13334/j.0258-8013.pcsee.170614.

[20] 陈海荣,徐政.适用于VSC-MTDC系统的直流电压控制策略[J].电力系统自动化,2006,30(19):28-33.

CHEN Hairong, XU Zheng. A novel DC voltage control strategy for VSC based multi-terminal HVDC system[J]. Automation of Electric Power Systems, 2006, 30(19): 28-33.

[21] 李海峰,刘崇茹,李庚银,等.适用于柔性高压直流输电网的直流电压下垂控制策略[J].电力系统自动化,2016,40(21):40-46.DOI:10.7500/AEPS20160401007.

LI Haifeng, LIU Chongru, LI Gengyin, et al. DC voltage droop-control strategy for VSC-based HVDC grid[J]. Automation of Electric Power Systems, 2016, 40(21): 40-46. DOI: 10.7500/AEPS20160401007.

[22] 尚磊,胡家兵,袁小明,等.电网对称故障下虚拟同步发电机建模与改进控制[J].中国电机工程学报,2017,37(2):403-412.

SHANG Lei, HU Jiabing, YUAN Xiaoming, et al. Modeling and improved control of virtual synchronous generators under symmetrical faults of grid[J]. Proceedings of the CSEE, 2017, 37(2): 403-412.

[23] WANG Haifeng, DU Wenjuan, Analysis and damping control of power system low-frequency oscillations[M]. New York, USA: Springer, 2016.

付 强(1993—),男,博士研究生,主要研究方向:新能源电力系统分析与控制。E-mail： 1197348393@qq.com

杜文娟(1979—),女,通信作者,博士,教授,主要研究方向:电力系统分析与控制,新能源电力系统。E-mail: 1376983331@qq.com

黄登一(1993—),男,硕士研究生,主要研究方向:新能源电力系统分析与控制。E-mail: 784035779@qq.com