非理想电网条件下的同步逆变器控制策略

陈 杰, 申朋朋, 魏 涛, 陈 新, 陈家伟

(1. 南京航空航天大学自动化学院, 江苏省南京市 210016; 2. 重庆大学自动化学院, 重庆市 400044)

0 引言

能源短缺和环境污染问题使基于可再生清洁能源的分布式发电和微电网技术得到广泛关注和发展[1-5]。发电系统与电网之间通过逆变器等电力电子接口互联,而常规电流控制型并网逆变器惯性小、抗扰动能力弱,无法体现电力系统固有的阻尼、惯性特点,很难为电网提供必要的电压、频率调节或支撑功能,而虚拟同步发电机(virtual synchronous generator,VSG)技术的优势正好弥补以上不足。

近年来,虚拟发电机技术方面,克劳斯塔尔工大提出的电流型和电压型VSG方案存在一定缺陷,电流型需要电流跟踪控制,其动态跟随性能将影响VSG特性;而电压型对定子电压采用开环控制,电压精度较差[6]。文献[7]利用VSG思想解决了虚拟同步机与实际同步机调速器时间常数不一致导致的动态功率分配不均问题,增强了并联系统稳定性。钟庆昌教授在此前研究基础上,提出了同步逆变器概念[8],细致模拟了同步发电机电磁暂态过程,使其具备常规并网逆变器欠缺的阻尼、惯性特征,建立了VSG技术中较为精确的二阶数学控制模型,为微电网提供必要的电压、频率调节或支撑功能。

关于VSG并网控制策略也已有一些研究报道。文献[9]针对双馈感应发电机提出了暂态电压补偿虚拟同步控制技术,解决了电网对称故障下转子过电流这一矛盾,但该控制策略加剧了直流母线电压波动,导致电磁转矩振荡时间被延长;而文献[10]仅对直接电压式VSG系统提出将虚拟阻抗与相量限流相结合的方法,有效限制了VSG故障电流暂态和稳态成分,但对电网故障下VSG的运行和控制没有研究,且应用场合有局限性。文献[11]分析了VSG有功—无功动态耦合效应导致的功率振荡问题,并通过有源阻尼控制策略抑制了谐振现象发生。然而,以上同步逆变器并网控制策略的研究大多在电网电压平衡或对称故障、不含背景谐波条件下展开。实际中,无功用户、非线性负载的大量接入,电网电压、电流均会发生畸变[12]。此时,若同步逆变器仍然采用理想电网条件下的控制策略,其输出电流中的不平衡成分和谐波成分将会污染电网,降低电网可靠性。而关于谐波或不平衡电网电压情况下,VSG并网控制策略的研究很少。仅文献[13]提出了一种适用于电网电压不平衡工况下VSG平衡电流控制策略,但该方法仅通过改变电流环基准来矫正入网电流,实际上电网电压在含背景谐波或不平衡工况下,入网电流不仅与电流环基准指令有关,还受到电网电压本身的影响。该控制策略并没有从本质上改善入网电流质量。

本文针对同步逆变器在非理想电网条件下的关键控制技术展开研究。首先构造同步逆变器电流内环,推导并讨论了非理想电网电压对同步逆变器入网电流的影响,提出了LC型同步逆变器在非理想电网条件下,入网电流谐波成分及不平衡成分的抑制方法,同时从逆变器输出阻抗的角度论证了所提策略对电网谐波的抑制机理。仿真和实验验证了理论分析的正确性。

1 同步逆变器及电流内环构造

1.1 同步逆变器功率外环

如图1所示,同步逆变器通过在功率外环中引入阻尼系数、无功积分系数、转动惯量等参数,使同步逆变器模拟同步发电机的一次调频和一次调压特性,并参照同步电机的数学模型,模拟出同步发电机的瞬时电磁转矩、无功功率及三相定子电势。使得同步逆变器较好地表现出同步发电机运行特性。图中:P和Q分别为系统有功功率及输出的无功功率;P*和Q*分别为给定有功功率基准值和系统无功功率的给定值;ωn为基准角频率;Tm为系统有功转矩给定值;Te为VSG的有功转矩;J为虚拟转动惯量;Dp为频率—有功功率下垂系数;ω为VSG角频率;θ为桥臂电势相角;Vm和V*分别为三相输出电压的幅值及其给定值;Dq为电压幅值—无功功率下垂系数;K为无功积分系数;if为电机转子励磁电流;Mf为电机定子绕组与转子绕组之间的互感系数;E为VSG内电势;Kpwm为归一化系数。

图1 同步逆变器控制框图Fig.1 Control block diagram of synchronverter

1.2 同步逆变器的电流内环构造

由图1可知,常规同步逆变器仅有功率外环,本质是一种间接电流控制方法,电流响应速度慢,当电网电压处于非理想条件时无法对输出电流进行有效控制。本节在功率外环基础上构造电流内环,以加快电流响应速度,改善电流波形质量,如图2所示。

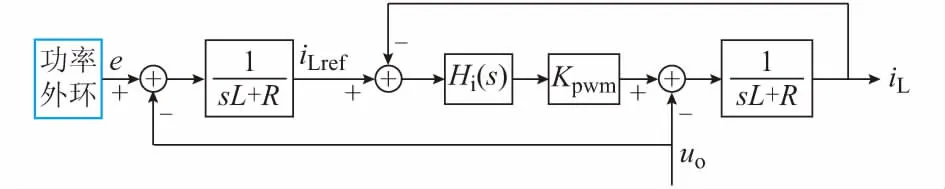
图2 同步逆变器电流内环控制框图Fig.2 Control block diagram of synchronverter with inner current loop

图2中:e为功率外环的输出,可等效为逆变器桥臂电势;L为三相输出滤波电感值;R为三相输出阻尼电阻值;iLref为电流内环基准;Hi(s)为电流内环调节器的传递函数;iL为电感电流采样值;uo为逆变器输出电压采样值。逆变器输出电压uo由采样得到,在输出滤波电感参数已知的情况下,可通过式(1)计算出电感电流参考值:

(1)

图2中Hi(s)为电流控制器,多采用比例—积分(PI)控制,但是PI控制需要进行三相坐标变换及dq轴之间的解耦计算,相对复杂,而比例—谐振(PR)调节器可以实现对交流信号的无静差跟踪,且实现相对简单。故本文选用PR调节器。调节器的输出通过脉宽调制(PWM)模块驱动开关管得到实际的桥臂电势输出。Kpwm为PWM驱动模块的调制系数,一般在系统中进行归一化处理,数值为1。

2 非理想电网条件下的控制策略

2.1 非理想电网影响分析

为了使逆变器在并/离网运行条件下具有相同的结构,本文采用了LC滤波器。当逆变器并网运行时,其输出电压uo即电网电压ug。附录A图A1给出了同步逆变器并网运行时的电流内环等效控制框图。

根据附录A图A1可推导并网电流表达式:

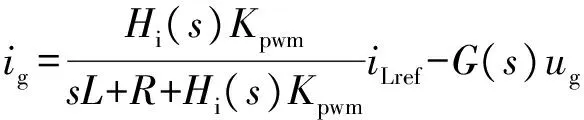
(2)

其中

(3)

(4)

式(2)表明,同步逆变器并网状态下的入网电流由电感电流参考值分量和电网电压扰动分量两部分组成。不同于常规并网逆变器的电流参考值完全由逆变器的有功和无功功率决定,同步逆变器的电感电流参考值还与电网电压直接相关,如式(4)所示。

当同步逆变器处于理想电网条件下并网运行时,电网电压仅含有基波正序分量,同步逆变器的电流参考给定也只包含基波正序分量。类似的,电网电压对入网电流的扰动分量也是三相平衡且不含谐波的。

然而,当电网不理想即三相电压幅值不对称或含有谐波分量时,电网电压可以分解为基波正序分量、基波负序分量和谐波分量。相应的,通过式(4)计算得出的电感电流参考值受电网电压影响,含有基波正负序分量和谐波分量;同时,电网电压对入网电流的扰动分量中也同样包含基波正负序分量和谐波分量。上述两处影响将会造成同步逆变器的输出电流不平衡且含有谐波分量,使得输出电能质量恶化,难以达到入网标准。

根据上述分析,在电网电压不对称和含有背景谐波两种条件下开展了初步的仿真验证,仿真条件如下。条件①:三相电网电压不对称,幅值分别为290,311,311 V;条件②:电压含有5%的5次谐波和7次谐波、2%的11次谐波和23次谐波。此处条件①的选取,满足电网运行规范要求,即电网中允许长期存在不平衡度小于4%的稳态不对称状态。

附录A图A2给出了两种不同条件下的并网电压和电流波形。由图A2(a)可知,电网电压不对称,不仅会造成逆变器输出电流严重不对称,而且会使得电流中包含低次谐波。而从图A2(b)的仿真结果中可知,当电网电压包含谐波分量时,也会使输出电流含有大量谐波,而且谐波含量被明显放大。

因此,有必要在同步逆变器原有控制策略基础上,寻求更加有效的控制方法,以抑制非理想电网对同步逆变器输出电流的不利影响。

2.2 电感电流参考值算法改进

2.1节的分析表明,非理想的电网电压可以分解成基波正序分量、基波负序分量和谐波分量。功率环带宽较低,在谐波频段内输出e只含有基波正序分量。但是,由式(4)计算得到的电感电流参考值仍然会受到非理想电网电压影响,含有基波正负序分量和谐波分量。若采用合适的方法提取电网电压的基波正序分量,用于电感电流参考值的计算,则参考值中只含有基波正序分量,入网电流会得到很大改善。

目前,常用的基波正序分量检测方法有滤波器检测法、自适应检测法、双二次广义积分检测法等[14-17]:其中,基于双二次广义积分的方法延时小、动态性能好,增加此模块不会给整个控制环节带来明显影响。故本文将选用该方法来提取电网电压基波正序分量,计算电感电流参考值。

附录A图A3为双二次广义积分器(DSOGI)结构框图。附录A图A3(a)为二次广义积分原理框图,其中vi为输入量,vo和qvo为二次广义积分器(SOGI)的两个输出量,vo和vi的基波正序分量幅值相等,相位相同,qvo和vi的幅值相等,但其相位滞后90°。vo和qvo对输入量vi的传递函数分别如下:

(5)

式中:k为待确定系数;ω0为正序基波角频率。

附录A图A3(b)为正序分量提取模块。图中:α和β分别为电网电压在两相静止坐标系下的α轴和β轴分量;α+和β+分别为所提取的电网电压在α轴和β轴下的基波正序分量。DSOGI分别构造α轴和β轴的两组正交信号α′,qα′和β′,qβ′,其中ω为谐振角频率,并网工作时为电网角频率。

系数k的取值不仅影响谐波分量与负序分量的抑制程度,而且影响系统的动态性能,需要折中考虑。关于k值的最佳选取设计,可以采用多目标优化算法来求取最佳解[18],以同时兼顾较好的稳态精度和动态跟踪性能。由于该内容不属于本文研究重点,故文中采用仿真分析的方法来确定k的最佳取值。仿真结果如附录A表A1所示。

附录A表A1所示为相同输入情况下不同k值时SOGI特性对比数据。其中SOGI的输入电压vi为含有5%的5次谐波和7次谐波、2%的11次谐波和23次谐波的电网相电压;在某一稳态时刻,基波成分幅值突减到原来的80%,5 s后,基波成分幅值又突增到原有值,由此突变工况来观察SOGI的动态特性。输出电压vo为提取的基波正序分量。由表A1可知,随着k值的不断减小,SOGI对基波正序分量的稳态提取精度越来越高,但动态特性不断变差,如k取值为8时,几乎可以瞬间跟踪幅值的突变(仅1个电网周期),说明其动态性能好,但稳态提取精度较差,谐波畸变率(THD)为5.91%;而当k取值为0.05时,SOGI对基波正序分量的稳态提取精度很高,THD仅为0.169%,但跟踪特性较差,大概需要0.44 s(22个电网周期)才跟踪上输入电压基波正序分量幅值的变化,说明其动态性能较差。以上仿真对比看出,为了兼顾SOGI的稳态精度和动态跟踪特性,k的取值不宜过大,也不能太小。权衡考虑,选取k值为0.5,此时稳态提取精度和动态性能均较佳,如表A1所示,提取出的基波正序分量几乎没有误差,THD仅为0.67%,且动态性能良好,仅需0.06 s,即3个电网周期。

基于DSOGI提取电网电压基波正序分量,将其应用到电感电流给定计算中,控制框图如图3所示。图中:C为三相输出滤波电容值;iC为三相输出滤波电容电流;ig为入网电流。如无特殊说明,电感电流参考值均为采用改进算法后的理想参考值。

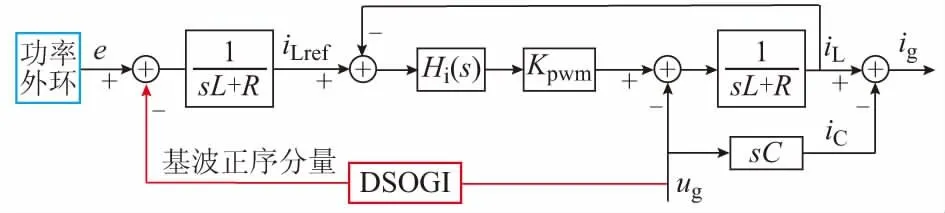
图3 电流参考值改进算法控制框图Fig.3 Block diagram of improved control method for current reference

2.3 电网电压前馈控制

常规单L型、LCL型并网逆变器并网运行时,电网电压的不理想会影响电网电流的质量。为抑制该影响,通常采用电网电压前馈的方法[19-20],在电网电压到网侧电感之间引入一条控制支路,增大逆变器输出阻抗,减小电网谐波对电流的影响。

本文采用了LC滤波器,当并网运行时,逆变器的入网电流不仅与电感电流有关,还与电容电流有关。因此,将并网逆变器电网电压前馈的方法运用到LC型同步逆变器中,能完全消除不理想的电网电压对电感电流的影响,但是入网电流仍受电网电压扰动。因此,需要找出适合于LC型同步逆变器的电网电压前馈策略,以更好地抑制电网电压对入网电流的影响。

从附录A图A1加入电流环的同步逆变器控制框图可以看出,在实际控制系统中,适合将电网电压信号前馈的位置只能是在电流控制器前和电流控制器后,如图4所示,其中A和B为待定的传递函数。

图4 改进型电网电压前馈控制框图Fig.4 Block diagram of improved voltage feed-forward control scheme

由图4可得到入网电流ig的表达式为:

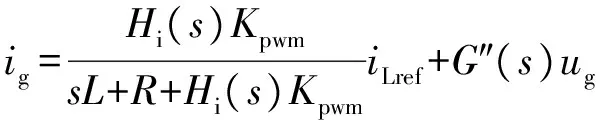
(6)

其中

G″(s)=

(7)

要彻底消除电网电压对电网电流的影响,须满足G″(s)=0,即

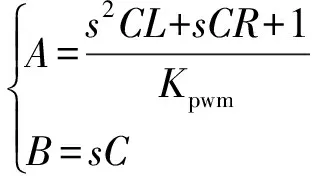
(8)

加入A,B两项电网电压前馈项之后,入网电流传递函数为:

(9)

式(9)表明,虽然本文采用电感电流iL反馈控制,但是采用图4所示的电网电压前馈控制策略后,可以使得电网电流ig严格跟踪电流参考值,且不受电网电压的不理想分量干扰,本文将此控制方法称为改进型电网电压前馈控制。

采用与2.1节中相同的仿真条件,即电网电压不对称和电网电压包含背景谐波两种情况,对改进型电网电压前馈控制进行了仿真分析,得到并网状态下电压、电流波形如附录A图A4所示。

对比附录A图A4(a)与附录A图A2(a)不难看出,改进型电网电压前馈控制方法有效消除了电网电压不对称对输出电流的影响。即使电网电压存在不对称,入网电流仍然具备良好的对称性;同时对比附录A图A4(b)与附录A图A2(b)可见,采用改进型电网电压前馈控制方法后,入网电流THD仅为2.55%,满足入网标准。因此,该改进型电网电压前馈控制方法可以有效抑制非理想电网引起的入网电流畸变,仿真结果初步验证了前文理论分析的正确性和所提控制策略的有效性。

2.4 同步逆变器输出阻抗特性分析

针对上述电感电流参考值改进算法和电网电压前馈控制策略对入网电流波形质量的改善作用,其本质是改变了逆变器输出阻抗。因此,本节将对同步逆变器的输出阻抗特性及其变化规律进行分析,从阻抗角度对谐波抑制机理给出一种可行的理论解释。在三相系统中,采用谐波线性化建模法对输出阻抗进行建模之所以分为正、负序两种,本质在于传统功率环在正、负序两种情况下,阻抗的表达式有所区别。本文控制策略是在传统功率外环下增加了电流内环,由于相对于内环来说,功率外环带宽很低,在阻抗建模过程中,其小信号扰动量对内环的影响可忽略不计。而为了便于理解,本文在对电流环分析时,等效为三个单相系统,即对单相电流环系统进行建模,故不需要分解到正负序下进行分析。

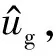
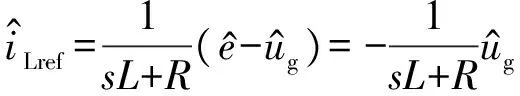
(10)

将式(10)代入式(2),可得式(11):

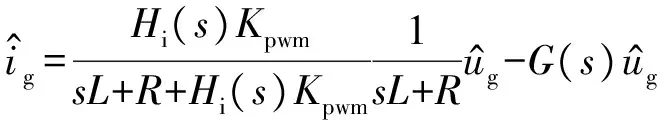
(11)

解得此时逆变器阻抗为:

(12)

根据式(12),可以绘出逆变器输出阻抗曲线,如附录A图A5中实线所示。为了验证模型正确性,通过仿真实测了不同频率下的输出阻抗幅值和相角,如附录A图A5中的黑点所示。可以看出,理论曲线与实测结果非常吻合,表明了式(12)阻抗表达的正确性。

类似的,对采用电感电流参考值改进算法和电网电压前馈控制策略后的同步逆变器输出阻抗也进行了建模分析,可推导得到逆变器A相输出阻抗为:

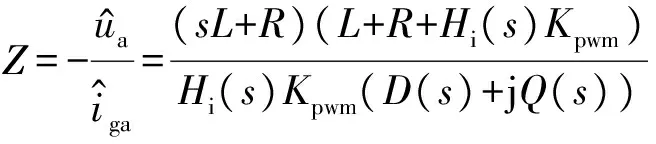
(13)

同样,通过仿真实测来验证输出阻抗表达式(13)的准确性,结果如附录A图A6所示。可以看出,数学模型与实测阻抗基本吻合。

对比采用改进型控制策略前后逆变器输出阻抗,如附录A图A7所示。采用电感电流参考值改进算法和电网电压前馈控制策略后,逆变器的输出阻抗幅值明显增大,即增强了对谐波抑制的能力,从而从阻抗的角度解释了为什么改进后的控制方法具有更好的谐波抑制能力。

3 实验与分析

为进一步验证所提控制方法的正确性和有效性,搭建了一台额定功率为7.5 kVA的同步逆变器样机,见附录A图A8,主电路开关管采用IPM模块,控制器采用TMS320F28335DSP,开关频率和采样频率均为20 kHz,其他参数见附录A表A2。

在电网三相电压不平衡(幅值大小与前文仿真一致,分别为290,311,311 V)条件下进行实验,图5(a)(b)(c)分别为电网电压波形、未采用本文所提控制方法的并网电流波形,以及采用本文所提改进型电网电压前馈方法的并网电流波形。不难看出,采用常规控制方法时,电网电压的不平衡会造成入网电流明显不对称,且波形严重畸变。图5(b)所示实验结果与附录A图A2(a)仿真结果完全吻合。

而当采用本文所提出的改进型电网电压前馈方法时,见图5(c),入网电流波形质量得到了显著改善。

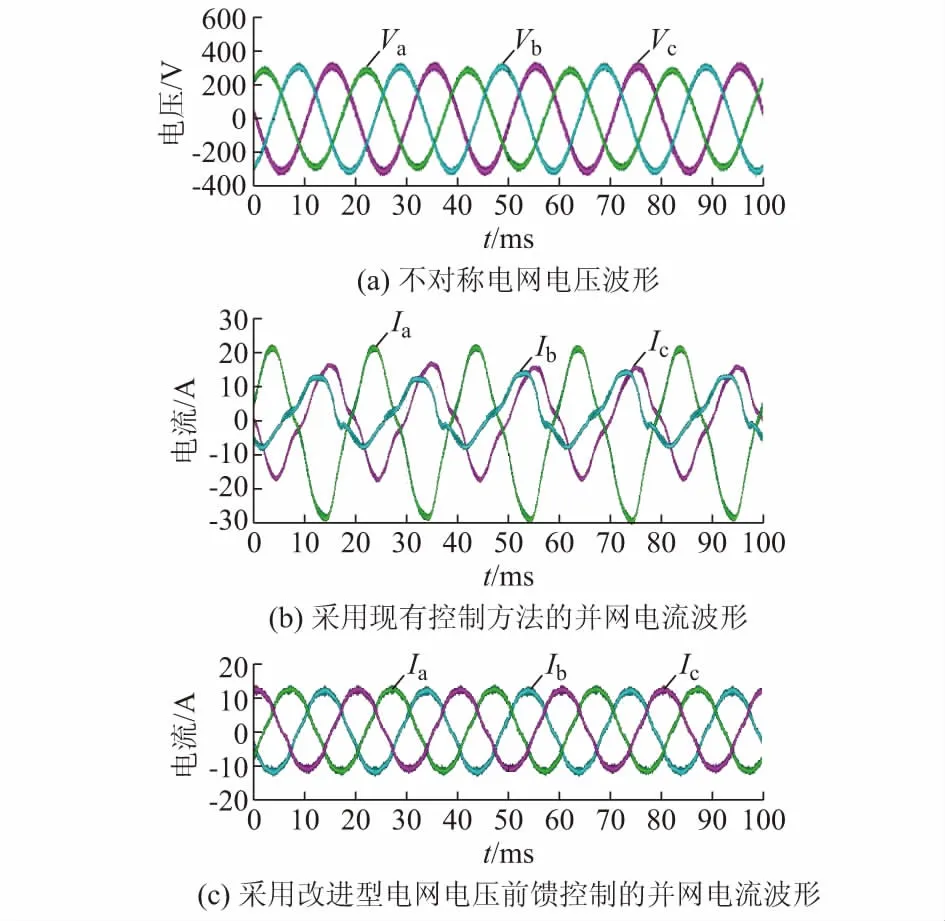
图5 电网不对称条件下的实验波形Fig.5 Experimental results under unbalanced grid condition

类似的,采用与附录A图A4(b)仿真研究相同的条件,即在电网中注入5%的5次谐波和7次谐波、2%的11次谐波和23次谐波,进行实验验证。图6(a)(b)(c)分别给出含谐波电网电压波形、常规控制方法的并网电流波形和采用本文所提改进型电网电压前馈方法的并网电流波形。对比图6(b)(c)不难看出,在非理想电网条件下,若不采用改进型电网电压前馈控制方法,并网电流波形畸变十分严重,而当采用本文所提控制方法时并网电流波形明显优于前者。这一点与附录A图A2(b)和图A4(b)的仿真结果也一致,进一步验证了本文所提改进型电网电压前馈方法的有效性和正确性。

需要指出的是,在仿真研究时,由于不存在电压、电流采样误差,电感、电容参数确定不变,因此前馈环节的补偿效果非常精确。而在实际实验过程中,电压和电流采样,电容和电感数值均存在误差,个别甚至随负载的变化存在一定的非线性特征,包括元器件的温漂造成前馈环节补偿效果存在误差等,这些实际的非理想因素都直接影响到了实验的控制效果,因此实验所得并网电流质量要比仿真中的并网电流质量略差。但是相对于常规控制方法得到的并网电流来说,本文所提的适用于非理想电网条件下的同步逆变器控制策略仍取得了令人满意的结果。此外,电压、电流的采样误差使得计算所得功率含有二倍频的波动,所以实验中并网电流不仅含有奇次谐波,还含有二次谐波。

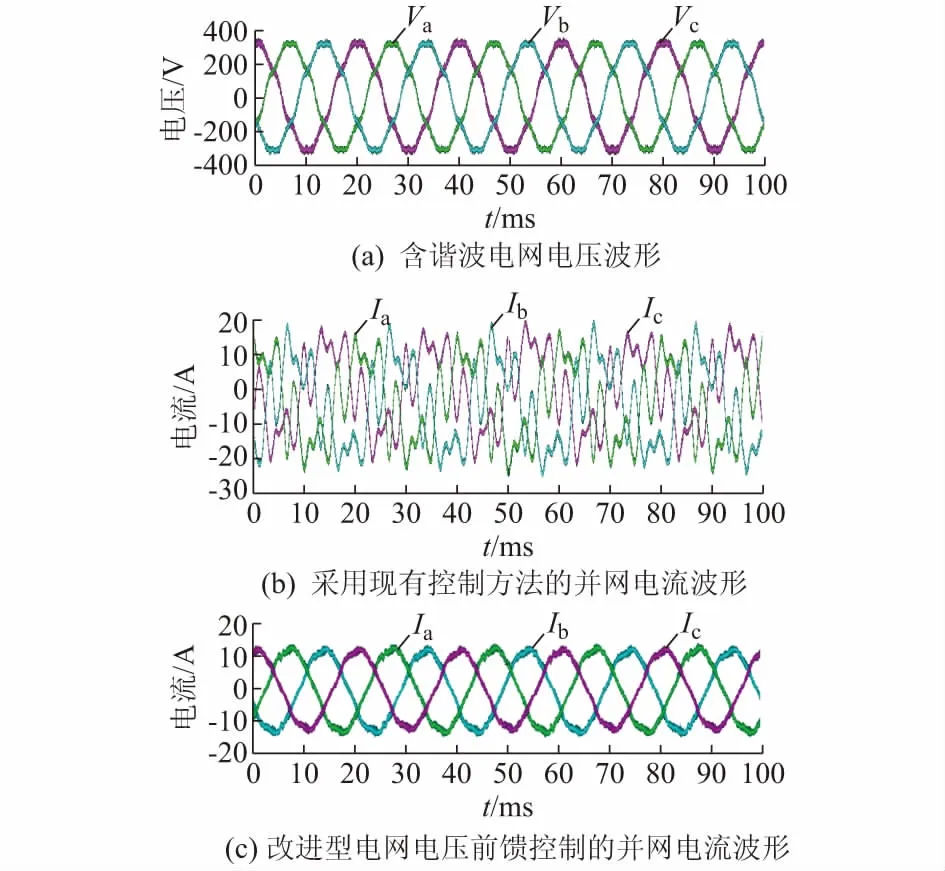
图6 电网含谐波条件下的实验波形Fig.6 Experimental results when grid voltage has harmonics

4 结论

为适应非理想电网电压工作条件,本文研究了一种基于电网电压前馈的控制策略。用双二次广义积分的方法提取电网电压基波正序分量来计算电感电流参考值,在此基础上,推导了LC型同步逆变器的电网电压前馈公式,利用电网电压前馈的控制方法抑制非理想电网条件对入网电流的影响。通过仿真和实验结果验证了所提控制策略的可行性,得到如下结论。

1)电网电压不理想会导致同步逆变器并网电流严重畸变。

2)提出了一种适用于LC型同步逆变器的改进电网电压前馈控制策略,该控制策略能较好地削弱电网电压畸变对并网电流造成的影响,确保并网电流可以满足入网标准。

3)实验中所得并网电流的波形劣于仿真结果,需要做进一步分析研究以提高电流质量。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] HONG Haifeng, HU Zhesheng, GUO Ruipeng, et al. Directed graph-based distribution network reconfiguration for operation mode adjustment and service restoration considering distributed generation[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(1): 142-149.

[2] 鲁宗相,王彩霞,闵勇,等.微电网研究综述[J].电力系统自动化,2007,31(19):100-107.

LU Zongxiang, WANG Caixia, MIN Yong, et al. Overview on micro-grid research[J]. Automation of Electric Power Systems, 2007, 31(19): 100-107.

[3] 王成山,肖朝霞,王守相.微电网综合控制与分析[J].电力系统自动化,2008,32(7):98-103.

WANG Chengshan, XIAO Zhaoxia, WANG Shouxiang. Synthetical control and analysis of micro-grid[J]. Automation of Electric Power Systems, 2008, 32(7): 98-103.

[4] ABAPOUR S, NOJAVAN S, ABAPOUR M. Multi-objective short-term scheduling of active distribution networks for benefit maximization of DisCos and DG owners considering demand response programs and energy storage system[J]. Journal of Modern Power Systems and Clean Energy, 2018, 6(1): 95-106.

[5] RAGHAVENDRA P, GAONKAR D N. Online voltage estimation and control for smart distribution networks[J].Journal of Modern Power Systems and Clean Energy, 2016, 4(1): 40-46.

[6] CHEN Yong, HESSE R, TURSCHNER D, et al. Improving the grid power quality using virtual synchronous machines[C]// Proceedings of 2011 IEEE International Conference on Power Engineering, Energy and Electrical Drives (POWERENG), May 11-13, 2011, Malaga, Spain: 6p.

[7] 赵杨阳,柴建云,孙旭东.基于虚拟同步发电机的柔性虚拟调速器模型[J].电力系统自动化,2016,40(10):8-15.DOI:10.7500/AEPS20150728014.

ZHAO Yangyang, CHAI Jianyun, SUN Xudong. Flexible virtual governor model based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2016, 40(10): 8-15. DOI: 10.7500/AEPS20150728014.

[8] ZHONG Q C, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.

[9] 程雪坤,孙旭东,柴建云,等.电网对称故障下双馈风力发电机的虚拟同步控制策略[J].电力系统自动化,2017,41(20):47-54.DOI:10.7500/AEPS20170225006.

CHENG Xuekun, SUN Xudong, CHAI Jianyun, et al. Virtual synchronous control strategy for doubly-fed induction generator wind turbines under symmetrical grid faults[J]. Automation of Electric Power Systems, 2017, 41(20): 47-54. DOI: 10.7500/AEPS20170225006.

[10] 尚磊,胡家兵,袁小明,等.电网对称故障下虚拟同步发电机建模与改进控制[J].中国电机工程学报,2017,37(2):403-411.

SHANG Lei, HU Jiabing, YUAN Xiaoming, et al. Modeling and improved control of virtual synchronous generators under symmetrical faults of grid[J]. Proceedings of the CSEE, 2017, 37(2): 403-411.

[11] 李武华,王金华,杨贺雅,等.虚拟同步发电机的功率动态耦合机理及同步频率谐振抑制策略[J].中国电机工程学报,2017,37(2):381-390.

LI Wuhua, WANG Jinhua, YANG Heya, et al. Power dynamic coupling mechanism and resonance suppression of synchronous frequency for virtual synchronous generators [J]. Proceedings of the CSEE, 2017, 37(2): 381-390.

[12] IEEE recommended practices and requirements for harmonic control in electrical power systems: IEEE Standard 519—1992[S]. 1993.

[13] 陈天一,陈来军,汪雨辰,等.考虑不平衡电网电压的虚拟同步发电机平衡电流控制方法[J].电网技术,2016,40(3):904-909.

CHEN Tianyi, CHEN Laijun, WANG Yuchen, et al. Balanced current control method for virtual synchronous generator considering unbalanced grid voltage[J]. Power System Technology, 2016, 40(3): 904-909.

[14] JOVCIC D. Phase locked loop system for FACTS[J]. IEEE Transactions on Power Systems, 2003, 18(3): 1116-1122.

[15] 马莉,周景海,吕征宇,等.一种基于dq变换的改进型谐波检测方案的研究[J].中国电机工程学报,2000,20(10):55-58.

MA Li, ZHOU Jinghai, LÜ Zhengyu, et al.An improved harmonic detecting approach based ondqrotating coordination transformation[J]. Proceedings of the CSEE, 2000, 20(10): 55-58.

[16] 刘云潺,黄纯,欧立权,等.基于dq变换的三相不平衡电压暂降检测方法[J].电力系统及其自动化学报,2007,19(3):72-76.

LIU Yunchan, HUANG Chun, OU Liquan, et al. Method for unbalanced voltage sag detection based ondqtransform[J]. Proceedings of the CSU-EPSA, 2007, 19(3): 72-76.

[17] 李林,郭源博,张晓华.复杂电网工况下基于CDSOGI-SPLL的电网电压同步方法[J].电力系统自动化,2017,41(16):151-157.DOI:10.7500/AEPS20161130016.

LI Lin, GUO Yuanbo, ZHANG Xiaohua. Voltage synchronization method of power grid based on CDSOGI-SPLL under the working condition of complex power grid[J]. Automation of Electric Power Systems, 2017, 41(16): 151-157. DOI: 10.7500/AEPS20161130016.

[18] 张东升.高功率因数VIENNA整流器控制策略的研究[D].哈尔滨:哈尔滨工业大学,2009.

[19] 吴云亚,谢少军,阚加荣,等.逆变器侧电流反馈的LCL并网逆变器电网电压前馈控制策略[J].中国电机工程学报,2013,33(6):54-60.

WU Yunya, XIE Shaojun, KAN Jiarong, et al. A full grid voltage feed-forward control strategy with inverter-side current feedback for LCL grid-connected inverters[J]. Proceedings of the CSEE, 2013, 33(6): 54-60.

[20] 韦徵,王俊辉,茹心芹,等.基于电网电压前馈补偿的光伏并网逆变器零电压穿越控制[J].电力系统自动化,2016,40(4):78-84.DOI:10.7500/AEPS20150316006.

WEI Zheng, WANG Junhui, RU Xinqin, et al. Zero voltage crossing control of PV grid connected inverter based on grid voltage feedforward compensation[J]. Automation of Electric Power Systems, 2016, 40(4): 78-84. DOI: 10.7500/AEPS20150316006.

陈 杰(1982—),男,博士,副教授,主要研究方向:微电网与分布式发电技术、电力电子变换装置的建模与控制技术、航空电源系统等。E-mail： chen_jie@nuaa.edu.cn

申朋朋(1992—),男,硕士研究生,主要研究方向:微电网与分布式发电技术、电力电子变换技术等。E-mail: 15651661780@163.com

魏 涛(1992—),男,硕士研究生,主要研究方向:微电网与分布式发电技术、并网逆变器的建模与控制技术等。E-mail: nuaa_wt@163.com

陈家伟(1986—),男,通信作者,博士,特聘研究员,主要研究方向:新能源发电技术和电网控制技术等。E-mail: echenjw@cqu.edu.cn