通过积分图多项式方法快速计算图像中心矩和Hu距
郭宇航
(国家新闻出版广电总局无线电台管理局,北京 100045)
1 引言
图像匹配和目标检测技术是现代图像处理的重要问题。进行图像匹配和目标检测通常的思路是提取图像中目标的特征,然后在其他图像中寻找这些特征。几何矩是图像中目标的重要特征,其形式简单,一般只需要一个数字就可以表达,所以常常被用来做一些粗略的区分。具有平移不变性的中心矩就是最常用的几何矩之一。但是由于光照、摄像头投影变形、拍摄角度、背景噪声等原因使同一个目标物体在图像中也会有很大变化,从而造成图像中目标的很多特征发生了改变。因此如果能寻找到图像中目标的一些特征,这些特征具有平移、旋转、灰度、尺度等的不变性,就可以根据目标的这些特征,在其他图像中寻找具有这些特征的区域图像进行匹配,进行可靠的图像匹配和目标检验。
图像的不变矩就是具有这些特点的一种浓缩的特征。1962年Hu.M.K提出了7个由几何矩生成的图像不变矩,图像平移、伸缩和旋转后,这些不变矩的值保持恒定[1]。由于Hu矩在很多畸变情况下的不变性,所以可以用Hu矩匹配进行目标的检测或快速的预处理,提取出目标可能的区域以进行下一步的处理。因为目标在图像中的大小、位置均未知,进行识别时,需要求出图像中不同位置和不同尺度的区域的Hu矩,然后和目标的Hu矩进行匹配。计算单一区域Hu矩比较复杂,如果针对图像中不同位置和不同尺度的区域,每个都求一遍Hu矩用来比较的话会使复杂度提升很多。
为了减少重复计算的复杂度、提高运算效率,采用积分图快速计算图像中任意位置和任意尺度矩形区域的灰度和的方法被提出[2]。基本原理是图像中任意一点的积分图的值定义为图像原点到该点所形成矩形区内各像点灰度之和。这样,原始图像中任意矩形区的灰度值之和就可以通过四个边界顶点的积分图值的加减法获得。当需要遍历某个图像中任意位置和任意尺度矩形区域的灰度和之值时,如果提前建立好积分图,然后通过积分图中四个顶点值的加减运算,会极大节省计算时间。
因为积分图的方法是将积分求值转化为四个顶点积分值的加减运算,所以比较适合化简一些图像像素的灰度值通过加减运算组合生成值的计算。但是图像中心距和Hu矩的值并不是简单地由图像像素的灰度值通过加减运算组合生成的,所以无法直接使用积分图来进行化简计算。本文对积分图的方法进行扩展,提出了一种积分图多项式的算法,可以用来化简遍历图像中任意位置和任意尺度矩形区域中心矩和Hu矩的计算。
2 Hu矩的积分图多项式计算方法
2.1 Hu矩的定义
f(x,y)是二阶连续函数,p,q为非零整数:0,1,2,3,…
f(x,y)的(p+q)阶原点矩m定义为:

f(x,y)的(p+q)阶中心矩μ定义为:
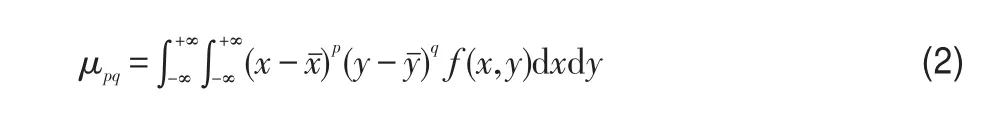

其中xˉ,yˉ和连续时同样定义

2.2 积分图方法

图1 积分图方法求某个矩形区域所有像素灰度值之和
如图1所示,在积分图中,左上方所有像素灰度值之和存储在每个点中:S其中图像(x,y)位置的像素灰度值用f(x,y)表示。积分图可以采用增量的方式生成:

初始条件:SAT(-1,y)=SAT(x,-1)=SAT(-1,-1)=0。所以为了求积分图,只需要对整张图像遍历一遍。有了积分图后,求图像矩形区域像素灰度值之和就简化为积分图中几个点数值的加减运算:

2.3 积分图多项式方法求Hu矩
由2.1中Hu矩的定义可知,Hu无法表示成像素灰度值的加减,但是可以用积分图多项式来表示。用积分图多项式求Hu分为3步:
(1)用积分图多项式来求原点矩
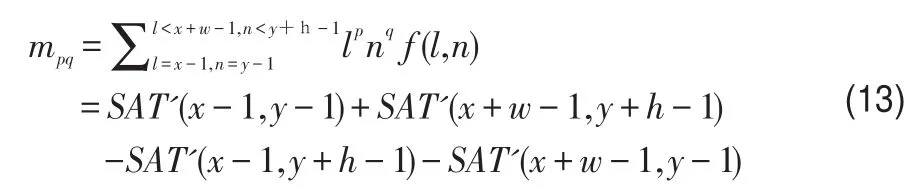
所以用mpnqf(x,y)作为每个像素对应的值。用增量的方法可以生成积分图用来快速计算原点矩:
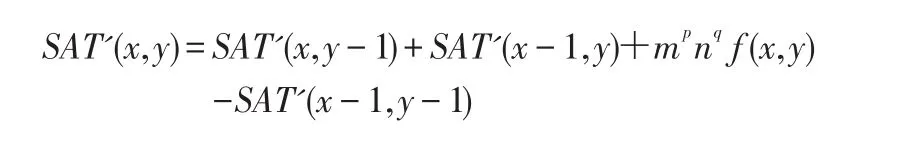
初始条件:SAT'(-1,y)=SAT'(x,-1)=SAT'(-1,-1)=0
(2)用积分图多项式求中心矩

矩形区域[x-1,y-1,x+w-1,y+h-1]的(p+q)阶中心矩:可以用积分图方法来计算。C(m,n)为从m个元素中任取n个元素的函数:
(3)用积分图多项式求Hu矩
用积分图多项式的方法计算下列各式:
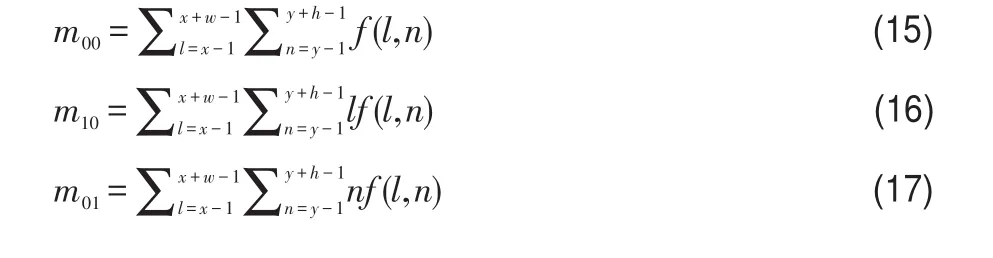

求得上述中心矩后,可以用本文公式(5)至(12)的方法计算Hu矩。
3 实验与结果

图2 原始图像

图3检测图像
实验目的为在图3中检测图2中的图像是否存在。方法为先求出图2的Hu矩,然后求图3中任意位置和任意尺度矩形区域的Hu矩。设定一个的阈值,如果图3中某个矩形区域的Hu矩和图2的Hu矩差别小于阈值的,则在图3中检测到图2的目标。遍历任意位置和任意尺度矩形区域采用枚举的方法,区域的宽度从2个像素到图片的宽度,区域的长度从2个像素到图片的长度,区域的起始位置也是从(0,0)开始,直到区域的边缘与图片的边缘重合。
求Hu矩采用两种方法进行对比:
方法1:传统方法,确定区域位置和尺度后,用公式(3)至(5)的方法计算归一化中心矩,用公式(6)至(12)的方法求Hu矩。
方法2:积分图多项式方法,先用公式(13)和(14)的方法建立广义积分图,确定区域位置和尺度后,用公式(15)至(32)的方法计算归一化中心矩,用公式(6)至(12)的方法求Hu矩。
实验采用的硬件:CPU为Intel i77700HQ,内存为16GB;采用的软件:操作系统为win10家庭版64位,程序运行环境为python2.7。
实验结果如表1所示,实验结果表明,方法2比方法1减少了很多计算时间,而且图片越大,方法2比方法1节约的时间越多。

表1 实验结果
4 结论与展望
由以上可知,利用积分图多项式的方法求图像中任意矩形区域的中心矩和Hu矩可以很大地减少计算时间,提高计算速度。此方法也可以在均值滤波、直方图均衡化等图像处理操作中进行推广。
参考文献:
[1]Hu M.Visual pattern recognition by moment invariants[J]. IRE Transactions on Information Theory,1962(8):179-187.
[2]Viola P,Jones M.Rapid object detection using a boosted cascade of simple features,2001.CVPR 2001.Proceedings of the 2001 IEEE Computer Society Conference on.IEEE,2001,1:I-511-I-518 vol.1.

