强化多种意识 破解程序框图
张 刚
(安徽省宿州应用技术学校 234000)
程序框图是实施新教材以来高考新增的内容,每年的全国各地高考试题均有所考查,大多以选择题或填空题居多,虽难度不大,但经常和高中数学的其他知识结合考查,也着实让不少同学难以处理,经常丢分,实属可惜.本文仅从程序框图在高考考查时需要关注和强化的几种意识加以总结,以期能对同学们的学习有所启发和帮助.
一、读图意识
例1 (2015高考新课标1,理9)执行右面的程序框图,如果输入的t=0.01,则输出的n=( ).
A.5 B.6 C.7 D.8

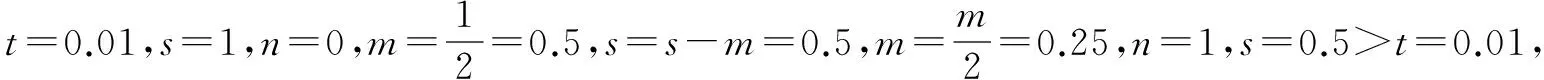
点评程序框图有很强的知识交汇性,可以和很多知识联系,因此,准确识别框图信息的算法功能是解题的关键.
二、验证意识

例2 (2016高考新课标1卷)执行右面的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足( ).
A.y=2x
B.y=3x
C.y=4x
D.y=5x
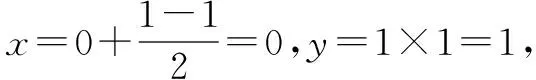
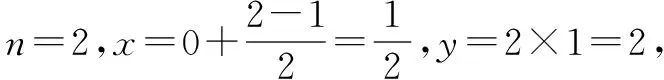
点评求解此类问题一般是按照程序将所给数值逐步代入,验证是否满足所给条件,最后列出运行结果.
三、列举意识

例3 (2014高考天津,理3)阅读右边的程序框图,运行相应的程序,输出的S的值为( ).
A.15 B.105
C.245 D.945
解S=1,i=1→T=3,S=1×3=3,i=2→T=5,S=3×5=15,i=3→T=7,S=15×7=105,i=4,结束算法,输出S=105,故选B.
点评框图以赋值框和条件框为主,注意条件框的要求是否满足,运行程序时要将执行的结果逐个例举,直至程序结束往往是最有效的办法.
四、累加意识

例4 (2014高考新课标Ⅰ,理7)执行右面的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=( ).
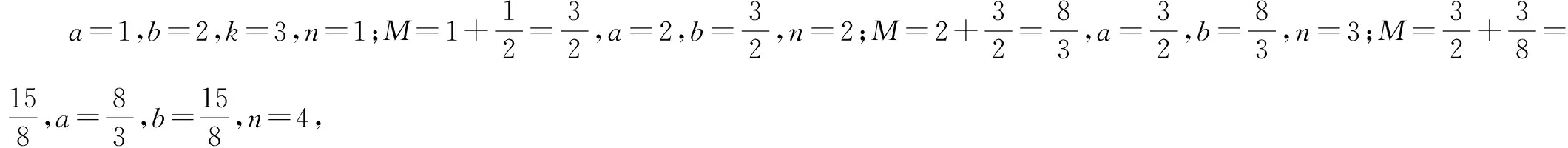
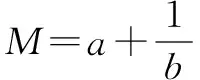
五、累乘意识

例5 (2014高考北京,理4)当m=7,n=3时,执行如图所示的程序框图,输出的S值为( ).
A.7 B.42
C.210 D.840
解当输入m=7、n=3,判断框内的条件为k<5?所以进入循环的k的值依次为7,6,5,因此执行S=S·k后,则由S=7×6×5=210.故选C.
点评本题中执行S=S·k是累乘化简的关键依据,另外,还要弄清程序退出的条件,是否满足,计算程序时要准确.
六、讨论意识
例6 ( 2014湖南高考,理6)执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于( ).

A.[-6,-2]
B.[-5,-1]
C.[-4,5]
D.[-3,6]
解当t∈[-2,0)时,运行程序如下,t=2t2+1∈(1,9],S=t-3∈(-2,6];
当t∈[0,2]时,S=t-3∈[-3,-1],则S∈(-2,6]∪[-3,-1]=[-3,6].故选D.
点评程序框图通过判断框实现了与分段函数的知识交汇,该题的解决过程体现了分类讨论的数学思想,注意分类讨论要做到不重不漏.
七、规律意识
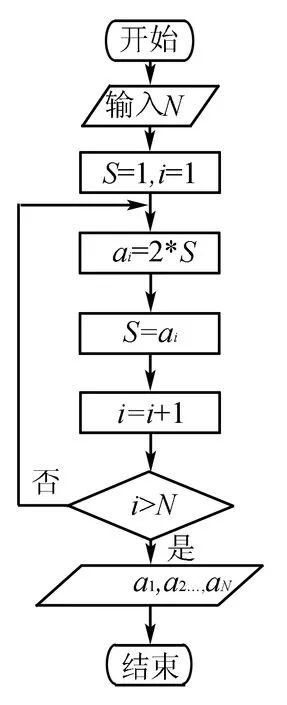
例7 (2014高考陕西,理4)根据右边框图,对大于2的整数N,得出数列的通项公式是( ).
A.an=2n
B.an=2(n-1)
C.an=2n
D.an=2n-1
解当S=1,i=1时,a1=2×1=21;当S=21,i=2时,a2=2×21=22;当S=22,i=3时,a3=2×22=23;…由此得到数列通项公式为an=2n,故选C.
点评读懂程序框图,逐次写出有限项,进而归纳总结出规律,是处理程序框图选择题最常用的策略之一.
八、线性规划意识
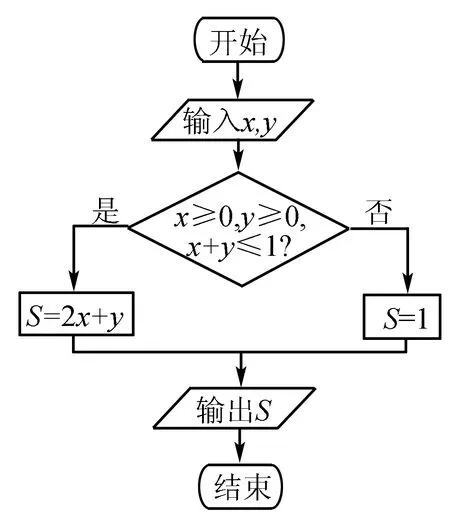
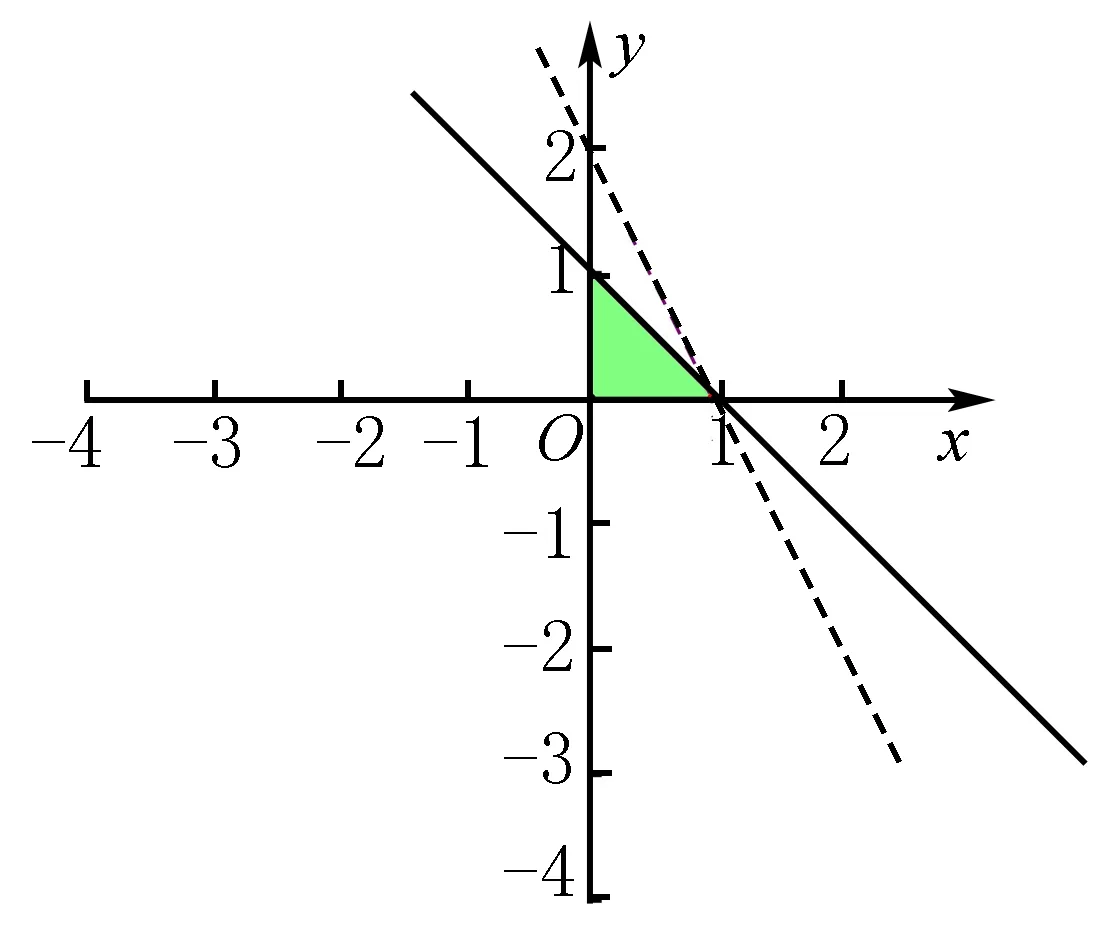
例8 (2014高考四川,理5)执行如图1所示的程序框图,如果输入的x,y∈R,则输出的S的最大值为( ).
A.0 B.1 C.2 D.3
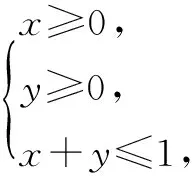

九、逆向思维意识

例9 (2015高考重庆,理7)执行如题(7)图所示的程序框图,若输入k的值为8,则判断框图可填入的条件是( ).

点评程序框图的条件补全问题是考查学生的逆向思维能力,是程序框图常见的题型,赋值计算判断,再计算一步,是解决此类问题的最有效的方法.
十、不等式意识

例10 (2014高考江苏,理3)右图是一个算法流程图,则输出的n的值是 .
解本题实质上就是求不等式2n>20的最小整数解.2n>20整数解为n≥5,因此输出的n=5.
点评主要考查不等式2n>20的最小整数解的问题.
十一、积分意识
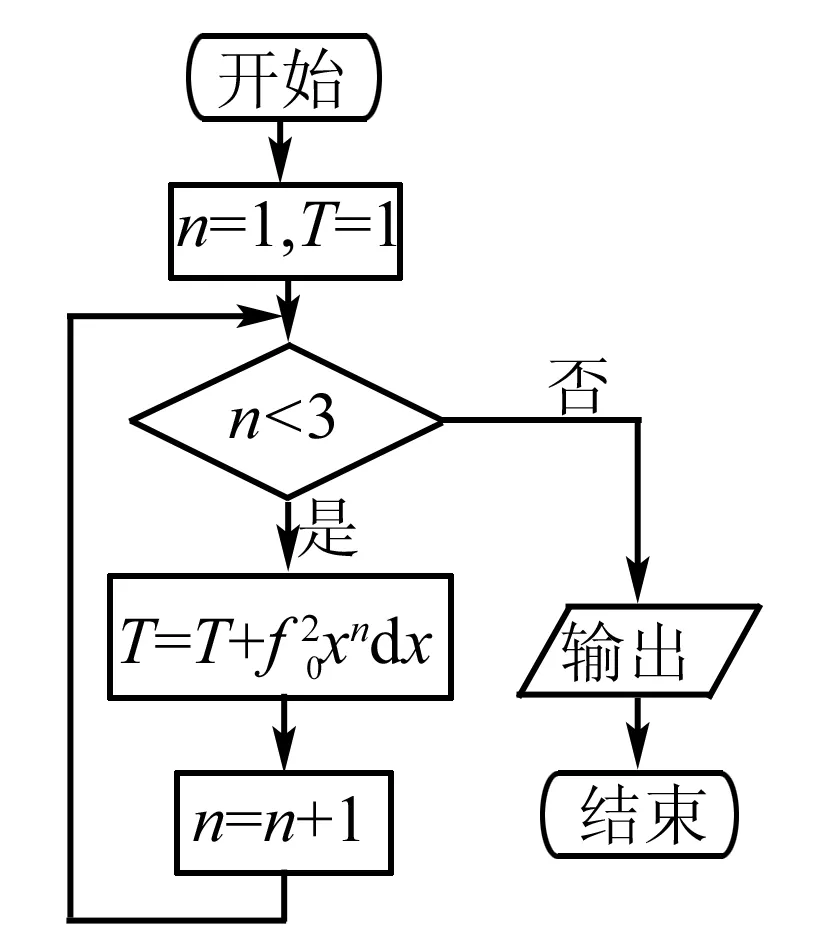
例11 (2015高考山东,理13)执行右边的程序框图,输出的T的值为_____.
解初始条件n=1,T=1,n<3 成立;
点评本题考查了循环结构与定积分的计算,意在考查学生对程序框图的理解和基本的计算能力,解题的关键是掌握定积分公式以及运算的准确性.
十二、递推意识

例12 (2015高考安徽,理13)执行如图所示的程序框图(算法流程图),输出的n为____.
解由题意,程序框图循环如下:
①a=1,n=1;
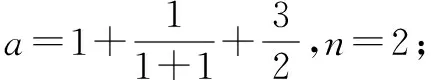

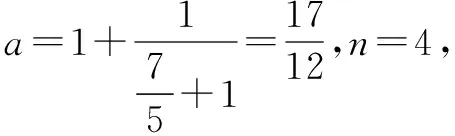
0.003<0.005,所以输出n=4
点评解决算法问题的关键是读懂程序框图,明晰顺序结构、条件结构、循环结构的真正含义,本题巧妙而自然地将算法、不等式、函数赋值交汇在一起,用循环结构来进行考查.这类问题可能出现的错误:①读不懂程序框图;②循环出错;③计算出错.
十三、新定义意识

例13 (2014高考湖北,理13)设a是一个各位数字都不是0且没有重复数字的三位数.将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=____.
解取a1=815,则b1=851-158=693≠815,所以a2=693;由a2=693,则b2=963-369=594≠693,所以a3=594;由a3=594,则b3=954-459=495≠594,所以a4=495;由a4=495,则b3=954-459=495=a4,
故输出b=495.
点评以新定义为背景,涉及算法与程序框图,其解题的关键是正确地理解程序框图中当型循环结构,并逐次判断循环体及其终止循环的条件,注意分清出当型循环结构和直到型循环体结构的区别.
由以上几例不难看出,程序框图题难度并不大,但考查的内涵却十分丰富,一不留神,就可能出错.当处理一个具体问题的程序框图时,到底应考虑哪种或哪几种意识,也并不是一成不变的,还是要依据题目的具体条件和自己平时的知识积累,具体问题,具体分析,方能以不变应万变.
参考文献:
[1]张刚.中学生数理化(高一)[J].郑州:河南教育报刊社,2017(01).

