充分发展管流中环塞的局部阻力特性

蔡书鹏，段传伟

(湖南工业大学 机械工程学院， 湖南 株洲 412007)

局部含有横截面积突然变化元件的管流，在石油、化工、水力、造纸等工业过程中经常遇到[1-5]。突扩、突缩是管路中典型的局部管件[6-8]，它们及其组合的局部阻力的准确评估是设计这种流动系统前必须调研的工作，因为它的大小直接影响着整个流动系统的设备及管件的选型。

纵观突缩管流的研究文献，有相当一部分，在测试局部阻力系数时，仅根据经验来确定上下游压力测点距突缩界面的距离，没有明确上游来流是近塞流、还是充分发展流(单位长度压差沿流向不再改变的流动)，这无疑会影响局部阻力系数的大小。大多数数值模拟研究都是在来流为塞流(断面速度均匀的流动)的条件下进行的，而实际上，理想的塞流是很难实现的流动。另一方面，已有文献大多仅涉及长径比较小的突缩流。但是，在化工以及轻工业中，管内流体的黏度较大，常常在管内结垢形成轴向塞状狭窄，有时轴向长度较大如在动物体的大动脉内，因胆固醇集结在血管管壁也会形成长径比较大的环塞状狭窄。研究管流中环塞的局部阻力特性对全面认识突缩管流必不可少，对揭示其水动力学机理具有深层次的学术意义。正是在以上研究背景和环境下，课题组拟选用不同孔径，在一个较宽的长径比范围内，对充分发展管流中内置的环塞的局部阻力特性进行测试，并运用分离流附壁实验对实验结果进行解释。

1 实验装置和实验方法

1.1 实验装置

为了在较大的雷诺数范围内在测试段形成充分发展的紊流，课题组采用多级叶片低脉动压力变频泵驱动水流的循环式流动装置，见图1。为了尽量避免水泵出口压力脉动、其它通流横截面变化导致的流动扰动进入测试段，在测试管入口段与水泵之间接入一个不锈钢板焊接的整流箱，整流箱内安装两道不锈钢丝网，它的主要作用就是流动准直，使进入测试段入口前的流动为接近断面内流速均匀分布的塞流。于是在测试段即可形成基本不受上游扰动影响，而主要由管壁诱导的流动猝发现象为主要成因的充分发展紊流。测试段管径D为10 mm，入口长度为100D。

图1实验装置示意图

1.2 实验方法

1.2.1 阻力测试

流速通过调节变频器频率改变转速来实现，流量通过电磁流量计测试，压差根据其估值大小分别采用不同量程的压差传感器测量。为确保将压差测点位于不受环塞影响的上下游的充分发展段内，课题组在距离环塞为20D和40D的上游三个位置布置静压测孔，见图1。在下游对称位置也布置三个静压孔。通过测试上游三孔、下游三孔间的压差，来判别静压测点是否位于充分发展紊流段内，若不是，应设法增加测试管长度、改变测压孔位置使其远离环塞。实验前，准备好6种规格的环塞，环塞的孔径比β=d/D(d为环塞内径)分别为0.5和0.8，每个孔径比的环塞有3种长径比l/d=0.2,0.5和1.0(l为环塞轴向长度)。

1.2.2 突缩管内流动附壁长度测试

当流动从一个大管(主管)进入到一个小管时，由于流动横截面积突变，在流体流动惯性作用下，流体不能继续与管壁贴合向前运动，而是在突缩入口开始脱壁形成分离流，在突缩管内某一位置，主流流束截面积最小形成缩颈，然后随流体继续向前，脱离壁面的主流将在距离突缩管入口某一距离位置再次附壁。从突缩入口到流动附壁，在主流与管壁之间形成反向流，流体附壁后进入边界层流动发展状态。如果环塞的轴向长度很短，流动还未完全附壁就进入主管，相当于以一个较大的突扩进入大管，局部损失就会相应增加。因此，为了阐明环塞局部阻力行为机理，需要对环塞内流动附壁位置进行测试。课题组通过径向钻孔将一簇轻质绒毛植入环塞内壁，且绒毛不能高于内壁0.5 mm，通过观察绒毛随流的摇摆方向来判别绒毛所在位置是否为流动附壁位置。如果绒毛摇摆方向很不稳定，说明绒毛所在位置为流动附壁位置；如果绒毛摆向上游，说明绒毛所在位置的流动为反向流；如绒毛摆向下游，说明该位置的流动为附壁后的下游流动。课题组使用了两种孔径比β=0.5和0.8，而长径比l/d同为12的环塞进行分离流的附壁长度测试。

2 实验结果和分析

2.1 环塞内流动再附长度特性

再附长度随雷诺数的改变行为如图2所示，图2中xr/r为突缩界面到再附点的无量纲附壁长度(xr为突缩界面到再附点的附壁长度；r为环塞半径)，Re为主管的雷诺数。

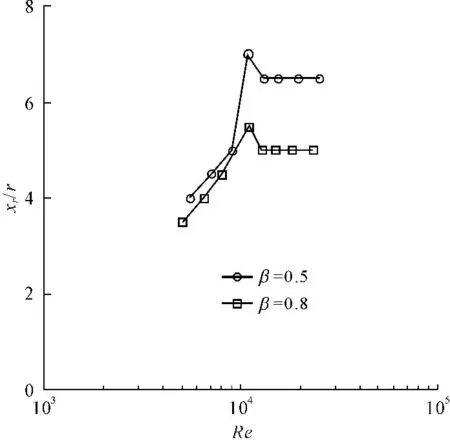
图2环塞内流动再附长度随雷诺数的变化特性

观察图2中的实验结果可知，随孔径比减小，再附点向下游移动，这是由于环塞内径减小，相应的管内流动惯性效应降低，不利于主流与反流区之间的质量掺混。当雷诺数较小时，无量纲的再附长度随雷诺数增加而增加，当达到最大值后，随雷诺数继续增大，稳定在一定值。当雷诺数较小时，增加雷诺数，主流“缩颈”位置向上游移动，但“缩颈”后主流束的扩大到附壁的距离却增加，其增加幅度超过“缩颈位置”向上游移动的改变量。而当雷诺数增加到一定值后，惯性效应加强了主流“缩颈”到附壁之间的紊流掺混，致使“缩颈”上移和附壁下移幅度相当，才使环塞内出现上述分离流的附壁行为。

2.2 单个环塞的局部阻力特性

为了验证本实验装置的可靠性和精度，课题组对未装有环塞的直管的沿程阻力系数进行了测试，其结果描述见图3。沿程阻力系数由下式定义：

(1)

式中：λ为沿程阻力系数；hf为两静压测点间的水头损失，m；L为两静压孔间距，m；U0为管内断面平均流速，m/s；g为重力加速度，m/s2。

实验结果显示，沿程阻力系数的试验点与布拉休斯经验值的偏差不大于3%，这说明本实验装置具有足够的可靠性和精度。

图3无环塞直管流的沿程阻力系数随雷诺数的改变

单环塞的局部阻力系数表示见图4。

环塞的局部阻力包括：近环塞的上游扰动流相对于充分发展流所额外消耗的压力损失、环塞内流动分离损失、流动发展损失(如果环塞足够长)、流出环塞进入主管内由于流束扩大而产生的局部扩大损失。当环塞轴向长度较小时，流动在环塞内未能附壁即进入突扩管内，局部损失的构成要更加复杂。在同一雷诺数下实测时，首先测试环塞上、下游所布置的两个测点之间的压差，通过压差确认其阻力系数与布拉休斯经验值的偏差在允许的范围内之后，方可测试跨环塞的上游充分发展流中的静压测点与下游同为充分发展流的静压测点之间的压差，并根据式(2)整理出环塞的局部阻力系数式(3)：

(2)

(3)

式(2)、式(3)中：p1、p2分别为上游和下游静压测点的静压水头，m；hl为环塞的局部阻力损失，m；l1为上游测点到环塞轴向中点的距离，m；l2为下游测点到环塞轴向中点的距离，m；λ1、λ2分别为环塞上、下游充分发展流段的沿程阻力系数。公式(2)的物理意义是显而易见的：插入环塞后的压差减去无环塞时相同压差测试段在充分发展流动条件下的压差即为环塞的局部阻力。

图4不同孔径比下单环塞局部阻力系数随Re的改变

对于孔径比β=0.5的环塞(见图4(a))，当长径比为l/d=0.2时，局部阻力系数ζ最大，约为15；而当l/d=0.5和l/d=1.0时，局部阻力系数基本相同，大小为9.3～9.7。由图2附壁长度的实验结果可知，当雷诺数Re>10 000时，无量纲附壁长度基本稳定在xr/r=7，因此对于长径比l/d=0.2的环塞，塞内的主流完全为脱壁且未能完成“缩颈”的分离流。流动离开环塞出口进入大管，由于流动惯性作用，主流束断面进一步缩小，完成“缩颈”后逐渐扩大直到流动在大管内重新附壁。环塞局部损失包括：上游近环塞的扰动损失、环塞内分离流的阻力损失、大管内以流束断面逐渐减小为特征的分离流损失、大管内从主流束“缩颈”开始经流动附壁后重新形成充分发展流的流束扩大损失。由于塞内距离短，导致主流束在大管内缩颈严重，因此大管内主流束断面逐渐缩小的分离流损失和其后的断面扩大损失都会加大，使得塞长最小的环塞局部阻力反而最大。这一实验结果能够解释，动物体内局部血管的狭窄比较大轴向长度的狭窄对血压升高的影响更大。对于长径比l/d=0.5和1.0的环塞，主流束在塞内完成了一部分流束断面缩小的流动，这使大管内流束断面的缩小程度相对降低。因此，在大管内的流束缩小损失和其后的流束扩大损失大幅度减低。

对于孔径比β=0.8的环塞(见图4(b))，当长径比为l/d=0.2时，局部阻力系数最大，ζ约为1.5；而当l/d=0.5和l/d=1.0时，局部阻力系数分别约为1.03和1.10。由图2的实验结果可知，当雷诺数较大时，无量纲附壁长度基本稳定在xr/r=5，这比β=0.5的附壁长度减小了30%。于是，虽然在局部阻力特性趋势上，β=0.8的环塞与β=0.5的环塞类似，但由于附壁长度减小，相同长径比时，流束断面缩小的流动在β=0.8的环塞内的时间比例比β=0.5的环塞大，加上孔径比增大效应，致使β=0.8的环塞的局部阻力系数，在其它条件相同时，仅相当于β=0.5的环塞的1/10。但环塞的长径比从l/d=0.5增加到l/d=1.0时，环塞内自身的流动损失加大，导致局部阻力系数加大。

2.3 双环塞的局部阻力特性

图5为两个相同规格的环塞以不同间距内置在充分发展管流中的双塞局部阻力系数，横轴x/d为两环塞的无量纲间距。

当第二个环塞放置在第一个环塞对下游流动的影响范围内时，两个环塞对下游流动的影响会产生相互干涉，作为宏观的干涉结果，双塞的局部阻力系数将不等于单个环塞的局部阻力系数之和；当两环塞间距超过单塞对下游的影响长度时，它们在对下游流动的影响上是相互独立的，具体体现在双塞的局部阻力系数将会等于单塞的局部阻力系数之和。由图5(a)可知，对于孔径比为β=0.5的两种长径比的环塞，当两塞间距小于6倍环塞内径(30 mm)时，两塞对流动的影响不是独立的，阻力系数远小于单个环塞的局部阻力系数之和；当两塞间距大于8倍塞径(80 mm)时，总的局部阻力系数ζ约为18，基本等于单个环塞的局部阻力系数的两倍，说明两塞对下游流动的影响是相互独立的。对于孔径比β=0.8的两不同长径比的环塞，当两塞间距大于5倍塞径后，双塞的局部阻力系数ζ基本等于单个环塞的局部阻力系数(约为1.1)之和，说明两塞对下游流动的影响开始独立。β=0.5的两相同规格的环塞之间的流动干涉范围大于β=0.8，这与2.1中关于再附点的实验结果相符合。白兆亮等[11]使用β=0.83的相邻两个孔板，实验研究了板间距对总阻力系数的影响，得出当板间距大于9倍板孔内径时，两孔板对流动的扰动基本是独立的，而小于9倍板孔内径时，总的阻力系数随板间距发生改变，与本研究的结果有一定的差异。其原因可能：一是他的上游孔板放置位置距离光入口距离太短(一般牛顿流体紊流的充分发展需要50倍以上管径的入口长度)，该位置的流动很可能尚未充分发展；二是他们测压使用的静压管读数分辨率低(可有1 mm的读数误差)；三是流量测量用的流水堰水平面高度的分辨率也不高。这种产生差异也可能是国产玻璃管的内径沿管轴方向的变化不同所引起。

图5不同孔径比下双塞的局部阻力随塞间距的改变特性

3 结 论

通过对内置在充分发展管流中不同规格环塞的局部阻力和流动再附点的实验测试，获以下结论：

(1) 对于孔径比较小的环塞，塞内的分离流要求较长的再附长度才能重新附壁。l/d=0.2的局部阻力系数约为15，相当于l/d=0.5和l/d=1.0的局部阻力系数的1.5倍。

(2) 当环塞的长径比较小时，短塞长的环塞局部阻力反而大于长塞长环塞的局部阻力。

(3) 孔径比减小时，双塞之间的流动干涉距离增大。

参考文献：

[1] Wang H, Xie S, Qingyi S, et al. Experiment study on pressure drop of a multistage letdown orifice tube[J]. Nuclear Engineering & Design, 2013,265:633-638.

[2] Ray S, Date A W. Friction and heat transfer characteristics of flow through square duct with twisted tape insert[J]. International Journal of Heat & Mass Transfer, 2003,46(5):889-902.

[3] 党 彦,王炳军,李红梅,等.泄洪洞工作闸室及陡坡明渠段体型优化数值模拟[J].水利与建筑工程学报,2016,14(2):163-166.

[4] 邱耀德,罗彬文,彭 高.水平突变管内流动形态的数值模拟[J].湖南工业大学学报,2015,29(1):48-51.

[5] Durrett R P, Stevenson W H, Thompson H D. Radial and axial turbulent flow measurements with an LDV in an axisymmetric sudden expansion air flow[J]. Journal of Fluids Engineering, 1988,110(4):367-372.

[6] 常 胜,牧振伟,万连宾.大口径玻璃钢管承接式接头局部水头损失系数探讨[J].水利与建筑工程学报,2016,14(4):89-101.

[7] 李栋浩,王文娥,葛茂生.突然缩小圆管的局部水头损失系数试验研究[J].水利与建筑工程学报,2011,9(4):22-24.

[8] 王亚林,朱德兰,张 林.插入式滴灌管局部阻力相邻影响研究[J].农业机械学报,2015,46(11):187-194.

[9] 三浦,斩田中，定司,等.管内オリフィス下流の变动成分に关する实验的研究[J]. 日本机械学会论文集(B编), 1992,58：3547-3551.

[10] 李 琳,白兆亮.有压管道孔板局部阻力相邻影响系数研究[J].水电能源科学,2016,34(5):107-109.

[11] 白兆亮,李 琳.有压管道中孔板相对间距对局部阻力系数的影响及其机理研究[J].水电能源科学,2015,33(1):177-182.

[12] Ai W. Energy dissipation characteristics of sharp-edged orifice plate[J]. Advances in Mechanical Engineering, 2015,7(8):1-6.

[13] Ding T M, Wang Y. Comparison research on hydraulic characteristics of three type's orifice plate[J]. Open Fuels & Energy Science Journal, 2015,8(1):43-46.

[14] Zhao T Y, Zhang J L. Experimental study of a simple pressure loss coefficient model for multi-hole orifice[J]. Harbin of Institute of Technology Journal, 2008,15(3):399-403.

[15] 薛 冬,田 淳.断面收缩比对齿墩式内消能工消能效率的影响[J].水电能源科学，2014,32(4):84-87.