数值模拟在渐扩式折坡消力池中的应用

郑梅玲，李辉成

(1.福建省电力勘测设计院， 福建 福州 350003；2.武汉大学 水资源与水电工程科学国家重点实验室， 湖北 武汉 430072)

目前我国中小型水利项目，特别是低水头引水工程在总的水利工程中占据较大比例。低水头引水工程一般建设在耕地面积大、人口较集中地区，此类区域的特点是河岸侧堤和河床底部的抗冲能力较较低，若消能措施处理不当，水流出闸后往往不能均匀扩散，造成主流集中，形成折冲水流，冲刷河岸及河床[1]；同时，当水流的弗劳德数比较小(Fr<4.5)时，泄水建筑物通常无法形成稳定的水跃，即低弗劳德数水跃，其消能率低，大量的余能流向下游[2]。当弗氏数Fr=1.0～1.7、共轭水深比值小于2时，水面会泛起较大波浪，形成波状水跃，波状水跃下的水流不能随翼墙扩散，仍保持急流前进，导致主流两侧发生回流，缩窄河槽有效过水宽度，增大局部单宽流量，加剧对枢纽工程下游岸坡的冲刷和对下游段建筑物的淘刷，严重影响工程的运行。

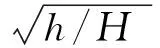
这些研究针对的或为顺坡渐扩式明渠、或为平底渐扩式消力池、或为仅折坡段扩散的消力池，而对于完全渐扩式折坡消力池水力特性的研究则少之又少。基于此，本文以河南省某水库工程南灌溉洞消力池为原型，按照重力相似原则，进行水工模型试验研究。针对原折坡等宽消力池即非扩散消力池方案中存在的不良流态、消能率低的问题，兼顾折坡式消力池和渐扩式消力池各自的特点，提出了一种全新的完全渐扩式折坡消力池形式，通过研究其流场的水力特性，阐明其消能原理。

本文运用数值模拟研究、模型试验验证的方法，对比了渐扩式折坡消力池和普通折坡消力池的消能效果差异，采用对消力池的流场的三维流态分析，发现了两者消能效果差异的原因，探明了渐扩式翼墙提高消力池消能效率的原理，为类似工程中折坡消力池的设计与体型优化提供借鉴。

1 数值模拟基本理论

1.1 三维数值模型

通过FLOW-3D软件来进行数值模拟计算研究，采用有限差分网格离散控制方程，再采用广义极小残差算法来迭代求解。

1.2 基本理论方程

对消力池的数值模拟计算属于气液两相流范畴。FLOW-3D对气液界面的描述为TruVOF方法，每个网格计算单元的流体体积分数满足方程：

(1)

(2)

F=1，表示单元被流体充满；F=0，表示单元被空气充满；F=0～1，单元内同时存在流体和空气。

1.3 湍流基本理论

湍流模型采用RNGk-ε理论模型，为解决高应变率和大曲率流线流动，RNGk-ε理论模型完善了平均流动中旋转情况和旋流情况下的流体运动，因而其精度较高，模拟结果更可信[8-13]。

(3)

(4)

式中：xj表示坐标轴j方向上分量；Gk是湍动能产生项的数值；μ为流体黏性值；ρ为流体密度值；t为时间量；p表压力值。

2 工程应用

2.1 计算体型及边界条件

2.1.1 工程概况及计算体型

某水库南灌溉洞孔口尺寸为2.5 m×2.5 m，为有压坝身泄水孔，洞身长24.4 m。洞身进口采用椭圆形曲线型式设计，进口底高程为81.5 m，布置事故检修闸门，洞身设有压平坡段，后接压坡段。涵洞下出口连接长20.0 m、深2.5 m的下挖式消力池，消力池后接南灌溉渠，涵洞出口处即消力池折坡为1∶4斜坡，与下底板连接为整个消力池部分。为降低消力池底板的扬压力，消力池底板水平段设置反滤和排水。

为研究渐扩式折坡消力池的消能效果，建立非扩散消力池和渐扩式消力池2种体型，两者除消力池翼墙型式有区别外，其余控制条件均一致。消力池模型示意图见图1。

2.1.2 计算网格

某水库南灌溉洞模型总共有31万个网格，其中参与计算的有效网格数约为14万个。因为模型在y方向长度远大于x向和z向长度，因此沿y方向设置三个网格块体，分别是包含水库计算域、闸室到消力池计算域和南灌溉渠计算域。其中闸室到消力池的计算域是本文重点研究范围，因此设置其加密网格尺寸0.001 m3，水库计算域设置为0.027 m3，南灌溉洞明渠计算域网格尺寸设置为0.064 m3。南灌溉洞网格划如图2所示。

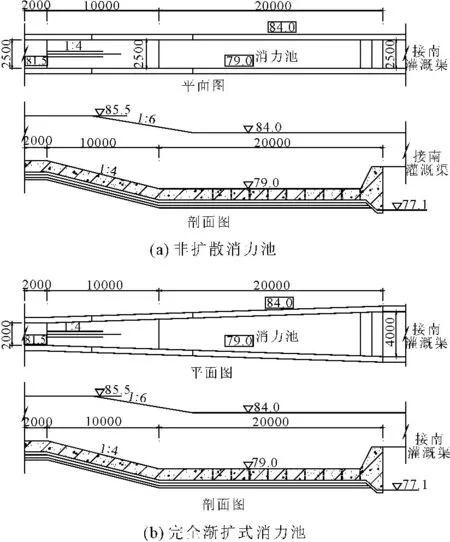
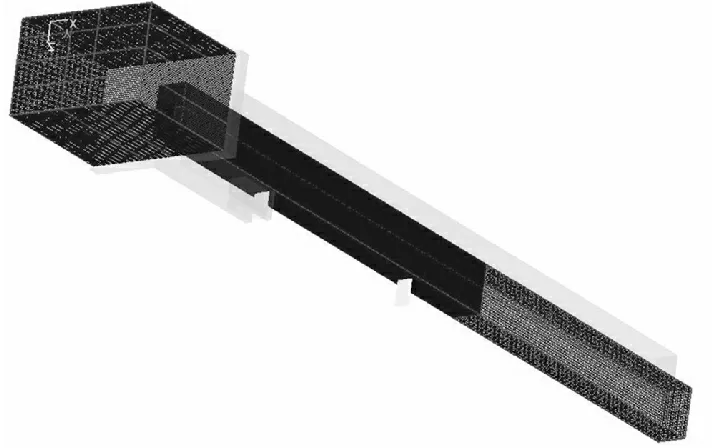
图1 消力池模型示意图(长度：mm，高程：m)

图2模型网格示意图

2.1.3 工况选取及数值模拟边界条件

在设计工况的控制条件下，对2种不同翼墙形式的消力池方案进行数值模拟计算，计算选取的工况如表1所示。

表1 数值模拟计算工况

计算边界条件设置：模型上部自由液面直接与空气连接，设置为压力进口边界。上游设置为设计流量工况下的库水位84.75 m，水面设置为自由水面，各结构壁面设置为固壁边界，糙率设置为混凝土糙率0.014。

2.2 模型计算结果对比分析

2.2.1 数值模拟结果可靠性验证分析

为确保数值模拟的准确性，对设计流量工况下水面线计算值与实测值进行比较，如图3所示：两模型中，消力池平坡范围内水面线吻合度很高，只是在折坡部分水面线略有差异；由于水跃发生在折坡段，该处流态较为复杂，模型试验时水流因卷气造成波动较大，水面线试验数据的误差不可控，由图3可知数值模拟与物理模型试验水面线拟合较好，数值模拟的计算成果可靠性较高。

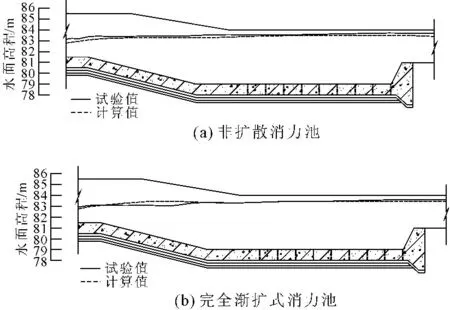
图3消力池水面线图

图4(a)为1∶20的水工模型中设计流量下消力池的流态，图4(b)为数值模拟流态稳定后的某一时刻的三维流态示意图，其中白色箭头表示水流的流速矢量。由图4可知，非扩散消力池水流在出闸后水面线收缩，流速最大，水跃发生在折坡略往上游处；完全渐扩式消力池的出闸流速比非扩散消力池方案大，水跃起始点比与前者略有延后，主要发生在消力池折坡起始点处。同时，两方案中消力池流态相似，仅在折坡起始处出现上下翻滚，均无立轴旋涡出现。这一点与物理模型试验一致[14]，可以发现FLOW-3D数值模拟的流态成果与试验吻合较好，且完全扩散式消力池并不会造成不良流态。

2.2.2 完全渐扩式消力池消能机理分析

以消力池折坡起点为Y0、折坡末端为Y10.0、 消力池末端为Y30.0， 将消力池中部平面轴线处的流速绘制成折线图， 见图5。 由图5可知， 完全渐扩消力池在折坡处流速减小梯度较大， 能量耗散较快。

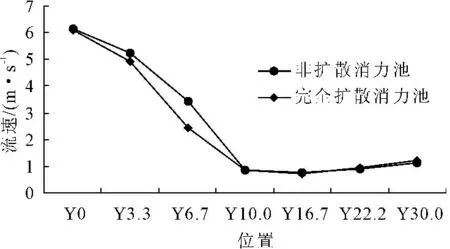
图4 消力池数值模拟流态图

图5消力池中部平面轴线处流速

数值模拟软件可以通过云图和等值线图展示各个剖面的流速分布情况，在分析流速分布方面有着试验点测流速不可替代的优势。由中部纵剖面速度云图6看出，在消力池内的水跃区范围内，完全渐扩式消力池较非扩散消力池的流速场分布更加紊乱，下部主流沿折坡向下后，又由底部向上翻滚，使水跃区水流上部不断翻腾漩滚，液体质点不断地穿越交界面进行交换，充分混合掺气，流速急剧变化。从各平面流速等值线看出，完全渐扩消力池上部和底部流速分布对称，中部流速等值线密集，流速梯度大，水流紊动剧烈，能量耗散快。从出池断面流速也可以发现，完全渐扩消力池低流速区部分有所扩大，即完全渐扩式消力池的消能更加充分，使出池水流动能减小。

2.2.3 完全渐扩式折坡消力池消能效率分析

紊动能是体现水流由紊动而产生的能量耗散程度的重要指标，其衡量流体的紊动状态，对考察水跃消能防冲建筑物性能具有重要意义[1,15]。本文采用的RNGk-ε二方程紊流模型可以计算水流的紊动能：

(5)

其中u′为脉动流速。计算结果见图7、图8。

对比两种消力池的中部纵剖面紊动能云图发现，完全渐扩式消力池的水跃紊动区向下更贴近消力池折坡，在沿流向上范围也更广；在水跃紊流中心区，非扩散式消力池动能最大值是1.58 m2/s2，而完全渐扩式消力池的最大值达到2.18 m2/s2。从中部平面的紊动能云图7可以看出，非扩散消力池的水流紊动区分布不明显，且紊动能较低；完全渐扩消力池的水跃区水流紊动集中在中部，中部漩滚区的紊动能值比非扩散消力池更大，水流紊动更明显。第三组对比图选取的是消力池折坡底部与平坡交界处断面的紊动能云图，由图8可以看出完全渐扩消力池的紊动水流在横向上向两侧扩展更明显。

2.2.4 消力池底板压强分布规律

消力池底板压强关系着工程运行的稳定与安全，本文通过数值模拟计算出消力池底板压强分布云图，见图9。

由图9可知，两种方案消力池底板压强分布规律相似，均由消力池平坡首部至消力池尾端递减，未出现超低负压区，最大压强约为42.5 kPa，满足工程结构安全要求。相较于非渐扩消力池，完全渐扩式消力池平坡首部压强梯度较大，消力池尾端压强也稍大。

3 结 论

(1) 本文应用FLOW-3D软件，采用RNGk-ε模型、TruVOF方法对完全渐扩式折坡消力池消能机理、消能效果进行数值模拟计算，以物理模型试验数据来验证数值模拟计算成果的可靠性，供类似工程参考。

图6 消力池各断面流速等值线图

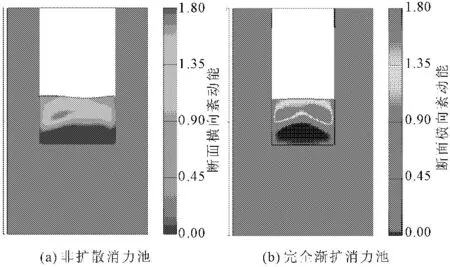
图7 消力池各断面纵向紊动能分布

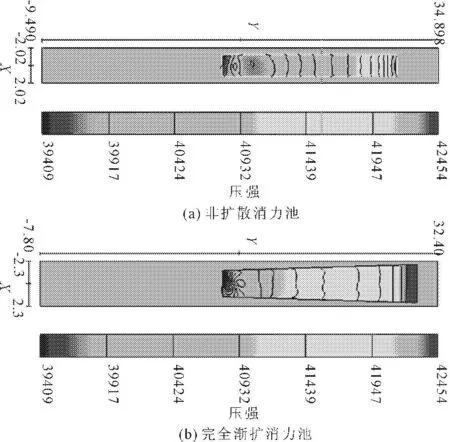
图8 消力池中部断面横向紊动能图

图9消力池压强分布

(2) 相对于非渐扩式消力池，渐扩式折坡消力池水流横向扩散明显，横向紊动剪切与摩擦冲撞增强了池内横向消能效果；同时，消力池中水跃发生区流速梯度更大，紊动剧烈，水流上下漩滚，掺气充分，纵向底流消能效果增强。完全渐扩式折坡消力池中横向消能与纵向底流消能相互结合使出池水流消能充分，水流流态平稳、流速分布均匀，对下游河床冲刷较小。

参考文献：

[1] Rouse H, Siao T T, Nagaratnam S. Turbulence characterics of the hydraulic jump[J], Journal of Hydraulics Division, 1959,84:1-30.

[2] 田振华,张术彬,韩 雷.钢筋石笼与混凝土消力池消能率对比试验研究[J].黑龙江水利科技,2014,42(11):16-19.

[3] 毛昶熙.闸坝泄流局部冲刷问题(四)——局部冲刷公式的推广应用[J].人民黄河,1988(6):65-68，49.

[4] 赵顺安,宋志勇.顺坡渐扩矩形明渠水跃计算公式[J].水利学报,2005,36(6):709-714.

[5] 吴宇峰,伍 超,刘小兵.渐扩散水跃跃长的研究[J].水科学进展,2007,18(2):210-215.

[6] 王冰洁,刘韩生.折坡扩散消力池水跃共轭水深计算方法及水跃长度、消能率分析[J].水电能源科学,2014(8):108-111.

[7] 梁 砚,周 赤,段文刚.折坡扩散型消力池的水跃特性试验研究[J].长江科学院院报，2017,34(3):53-57.

[8] 职保平，等.小石峡水电站溢洪道消力池结构优化的三维数值模拟[J].水利与建筑工程学报,2011,9(5):15-17.

[9] 木克然·阿娃，等.阿拉沟水库溢洪道流场数值模拟[J].水利与建筑工程学报,2014,12(2):38-43.

[10] 赵相航，等.基于VOF模型的台阶式溢洪道数值模拟[J].水利与建筑工程学报,2016,14(3):143-148.

[11] 王 昊，等.某重力坝泄洪底孔水力特性的数值模拟研究[J].水利与建筑工程学报,2016,14(2):40-44.

[12] 包中进,刘 云,王月华.泄水建筑物三维水流数值模拟技术及应用[J].浙江水利科技,2015(1):18-22.

[13] 胡松海.基于FLOW-3D软件溢流坝不同鼻坎角度的三维数值模拟[J].人民珠江,2017,38(8):72-75，83.

[14] 彭 诚,王均星,郑梅玲，等.渐扩式折坡消力池的水力特性试验研究[J].水电能源科学,2016(5):110-112.

[15] 董宗师,王均星,蔡 芳.非完全宽尾墩消能机理数值模拟[J].武汉大学学报(工学版),2016,49(4):521-526.