整体化铺装层加固空心板理论最优厚度分析

刘 发 水

(福州市公路局， 福建 福州 350002)

空心板桥因具有自重小、建筑高度较低、受力明确、结构简单、用料经济、施工快捷等诸多优点而被广泛应用，是我国高速公路、城市道路建设的主力桥型之一。然而调查显示部分空心板桥梁在超限交通量和运输作用下产生各种病害，需要进行加固改造[1-4]。

早期实际工程中，在荷载的长期反复作用下，桥面铺装层与主梁的粘结经常受到破坏。因此，结构上出于安全考虑，偏于保守的将铺装层作为安全储备，不考虑其参与结构受力，仅视为二期恒载作用[5]。但是，随着研究的不断深入，Seible F等[6]通过对实桥旧梁上浇筑混凝土铺装层的试验研究，发现桥面铺装层混凝土对主梁承载力有提高作用。鬲鹏飞[7]计算并分析了整体化铺装层对装配式箱梁桥在横向传力方面的影响，认为整体化铺装层可以有效提高装配式箱梁桥横向传力的性能。郝宪武[8]通过实际工程和有限元分析，对整体化铺装层对预应力箱梁桥承载能力的提高幅度以及设计计算方法开展了一些有益尝试。商允福等[9]为了解决低荷载等级桥梁改建成高荷载等级桥梁遇到的问题，在实践的基础上总结出预应力空心板桥超荷载设计方法，其实质是将铺装层和空心板视为组合截面共同承担外荷载的作用，但研究缺乏必要的试验依据。方萍等[10]通过对钢桥面上加铺沥青混凝土铺装层开展试验和有限元理论分析。分析结果表明：钢桥面能与沥青混凝土铺装层形成组合截面，共同承担荷载的作用。罗立峰等[11]通过结构线弹性理论简化得到以梁板体的最大弯矩为基础，以桥面铺装层的开裂和剥离为控制指标的水泥混凝土桥面铺装层计算方法。徐洪涛[12]通过6片2 m的矩形截面梁缩尺试验模型，分析了混凝土铺装层和钢纤维混凝土对主梁承载力的影响，认为桥面铺装层能够有效地提高主梁承载力。唐国斌等[13]通过在3片10 m的空心板上进行有无铺装层、不同材料铺装层的试验研究，分析了不同铺装层厚度和材料下的空心板桥受力性能，提出了考虑铺装层叠合效应的空心板桥计算方法。邹兰林等[14]通过有限元计算与荷载试验研究发现装配式板桥80%～90%的桥面铺装层参与结构整体受力比较符合结构实际受力状态。

目前，国内外学者对于中小跨径桥梁的整体化铺装层对主梁受力性能影响的研究较少。仅发现桥面整体化铺装层能够提高空心板桥的整体刚度，与空心板共同承担外荷载。但是整体化铺装层的有效厚度取值问题一直没能得到很好的解决，现行《公路桥涵设计通用规范》[15](JTG D60—2015)只对各种情况下桥梁的铺装厚度提出要求，但未详细说明铺装层有效厚度。随着新材料、新工艺的采用，桥面铺装与主梁的粘结越来越紧密，可以形成叠合结构，协同受力。因此，考虑桥面铺装参与受力是合理的。本文以装配式空心板桥为研究对象，采用大型通用软件ABAQUS建立有限元计算模型。分析了不同跨径的空心板桥，不同整体化铺装层厚度对应力和挠度的影响，讨论了不同跨径下整体化铺装层的理论最优厚度，并对不同跨径下考虑铺装层叠合效应的空心板桥进行了承载力极限状态和正常使用状态验算。

1 整体化铺装层加固设计

和普通铺装层的单层钢筋相比较，整体化铺装层采用双层钢筋网，并通过植筋与主梁连接，使主梁和铺装层形成叠合结构。整体化铺装增大了空心板截面高度、提高了结构整体抗弯刚度和铰缝传递荷载的能力，降低了荷载作用下挠度和应力值[16-17]。

如图1所示，本文以一跨8 m装配式空心板桥为例，介绍整体化铺装层加固设计。空心板中板宽1.24 m，高0.4 m。如图2所示，空心板顶部预埋顶部连接钢筋(①号钢筋)。铰缝采用深铰缝形式，共有剪刀钢筋和纵向受力钢筋两类构造钢筋。空心板和铰缝混凝土均采用C30，普通钢筋采用HRB335。

图1空心板横截面图(单位：cm)

图2铰缝构造图(单位：cm)

整体化铺装层混凝土采用C40级混凝土，厚度为22 cm，横向布置图如图3所示，铺装层配置上下两层钢筋网(钢筋①②)，每层布置图如图4所示，采用Φ16钢筋，间距10 cm×10 cm，在上层钢筋网靠近桥台处离端部2 m范围内进行钢筋加密(钢筋③)，加密钢筋为Φ16钢筋。植筋采用直径Φ16的钢筋，横桥向共布置四道植筋，间距34 cm，外侧植筋纵桥向间距30 cm，内侧植筋纵桥向间距60 cm，每片空心板上有78根植筋，总数为234根，布置如图5所示。

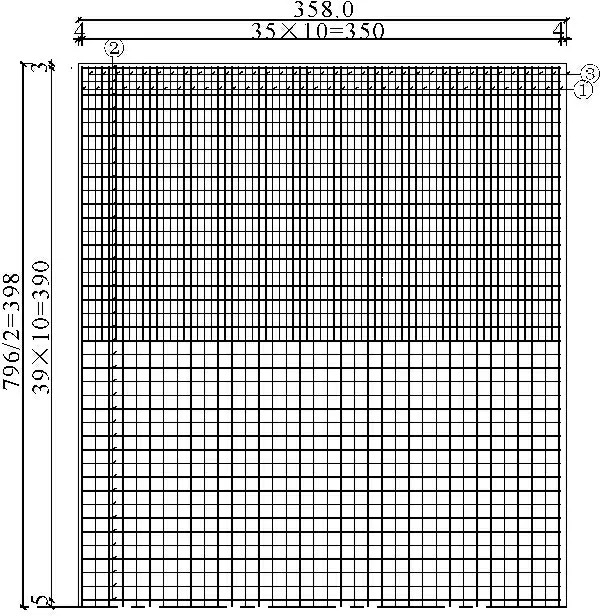
图3 空心板加固改造后横断面图(单位：cm)

图4 整体化铺装层钢筋网布置图(单位：cm)

图5植筋布置图(单位：cm)

2 采用整体化铺装层加固的空心板受力过程分析

分析装配式空心板桥的施工过程，可以将空心板桥的受力变化划分为三个阶段。

阶段一为空心板承受自重。此阶段空心板旧铺装层已凿除，空心板仅承受自身的重量。本阶段跨中截面弯矩计算如式(1)：

(1)

式中：q1为空心板自重集度；L为空心板计算跨径。

阶段二为空心板承受自重和整体化铺装层湿重。此阶段浇筑整体化铺装层混凝土，但尚未形成强度，空心板需承受自身的重量和整体化铺装层混凝土的湿重。本阶段跨中截面弯矩计算为：

(2)

式中：q2为整体化桥面铺装自重荷载集度，q2=γA；γ为混凝土重度；A为单片空心板整体化铺装层混凝土横截面面积。

阶段三为空心板与整体化铺装层共同承担外部荷载作用。此阶段整体化铺装层混凝土已形成强度，空心板与整体化铺装层形成叠合结构，共同承担汽车荷载等外荷载。

3 空心板桥整体化铺装层厚度对空心板桥受力性能影响分析

3.1 参数选择

取空心板桥标准图跨径6 m、8m、10 m、13 m、16 m和20 m的简支空心板进行整体化铺装层加固空心板桥理论最优厚度评价，各跨径空心板的技术指标如表1所示。

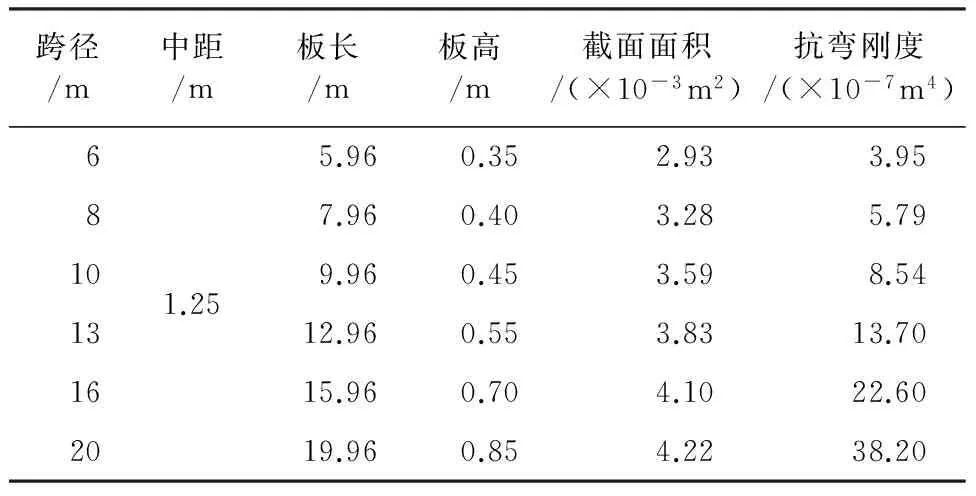
表1 空心板桥主要技术指标表

3.2 有限元模型

采用通用非线性有限元软件ABAQUS，建立整体化铺装层加固后空心板的实体有限元计算模型。空心板、铰缝和整体化铺装层采用线性减缩积分的三维六面体单元C3D8R，空心板主筋和铰缝门式钢筋采用三维三节点桁架T3D2单元，全桥有限元模型见图6。采用Embedded功能模拟混凝土和钢筋的相互作用。采用Tied约束实现铺装层与主梁和铰缝的连接。

图6有限元计算模型

有限元中空心板桥梁端采用简支约束。根据桥梁跨径及最不利原则,汽车荷载采用公路-Ⅰ级车道荷载，根据最不利工况(偏载)进行加载，偏载工况示意图如图7所示。

采用塑性损伤模型模拟混凝土的塑性阶段行为[18]。采用理想弹塑性模型模拟钢筋，弹性模量Es取200 GPa，屈服应变μs为1 675 με。空心板与铰缝的接触属于新老混凝土接触问题，新老混凝土粘结强度可以分为法向轴拉粘结强度ft、两个沿着结合面表面方向的粘结剪切强度τy、τz。结合面法向轴拉粘结强度ft取新、旧混凝土中较小的轴拉强度值的70%[19]；采用刘沛林等[20]双折线模型来模拟空心板与铰缝构造的结合面的粘结滑移关系，τy和τz两个方向的粘结滑移关系是相同的；结合面的粘结滑移刚度K取10 MPa/mm；最终滑移值Su和峰值应力对应的滑移值S0之比Su/S0取2.0[21]。

图7车辆荷载布置示意图(单位：cm)

对比某空心板桥整体化铺装层一跨8 m足尺模型试验[22]，跨中截面荷载-挠度曲线和荷载-应变曲线如图8、图9所示。从图8、图9中可以看出，空心板的试验值和有限元值基本一致，整体的变化趋势也近似相同，说明了本文有限元模型的正确性，可以进行进一步参数分析。

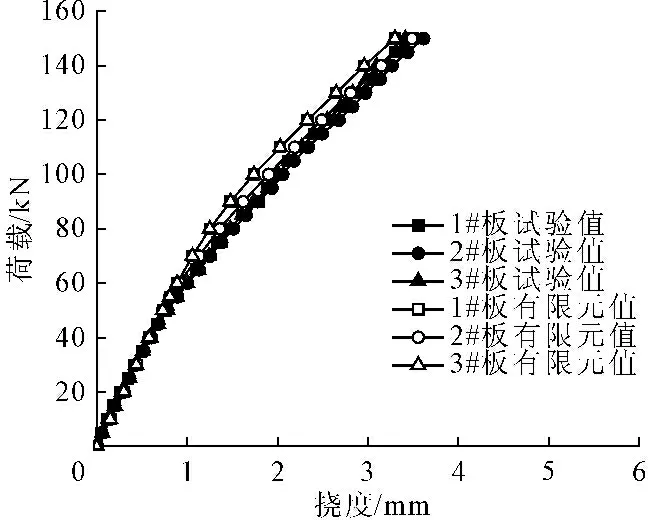
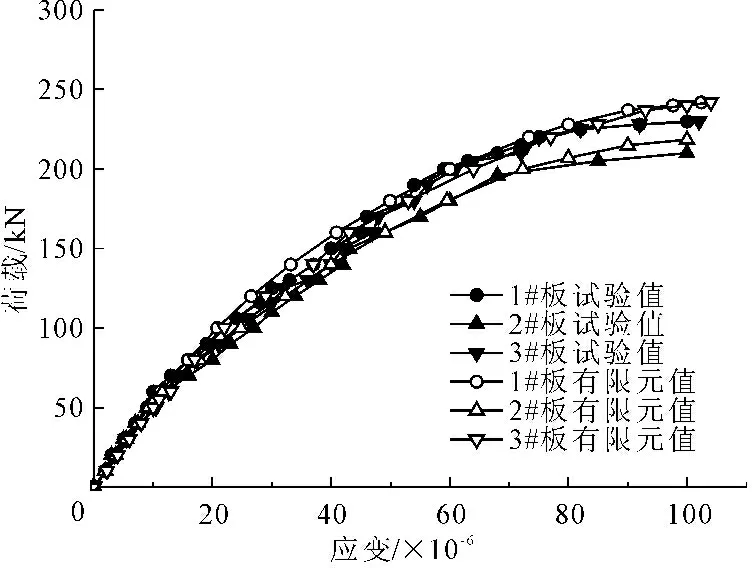
图8 空心板跨中截面荷载-挠度曲线

图9空心板跨中截面荷载-应变曲线

3.3 整体化铺装层厚度影响分析

图10是L=6 m时不同整体化铺装层厚度情况下，结构自重、汽车荷载和组合作用下空心板应力和挠度曲线图。在桥面铺装层混凝土尚未形成强度之前，铺装层的自重由空心板承受，故应力和挠度随着铺装层厚度的增加而增大，曲线呈上升状态。在铺装层混凝土形成强度以后，铺装层与空心板形成叠合结构共同受力，整体刚度变大。在一定的外荷载作用下，随着铺装层厚度的增加，应力和挠度逐渐减小，曲线呈下降状态。

虽然随着铺装层厚度的增加，铺装层混凝土自重在结构的总应力和总变形中占有越来越大的比例，但是总应力和总变形与铺装层的厚度并不是一个线形的关系。随着铺装层厚度的增加，组合作用下的应力与挠度曲线均呈先下降后上升的状态，存在一种整体化铺装层厚度值，使得在相同荷载作用下空心板的应力或挠度最小。对于跨径L=6 m的空心板，铺装层厚度为30 cm时，空心板应力最小；当铺装层厚度为26 cm时，空心板挠度最小。

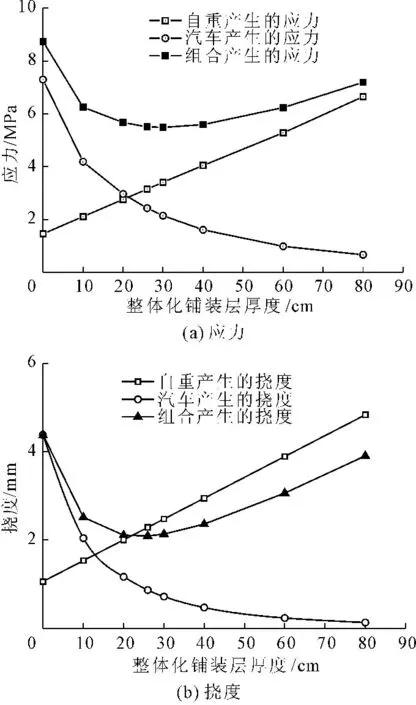
图10不同整体化铺装层厚度下空心板应力与挠度曲线(L=6 m)

同理，通过研究表明：跨径L=8 m的空心板，铺装层厚度为24 cm时，空心板应力最小；当铺装层厚度为20 cm时，空心板挠度最小。跨径L=10 m的空心板，铺装层厚度为20 cm时，空心板应力最小；当铺装层厚度为15 cm时，空心板挠度最小。跨径L=13 m的空心板，铺装层厚度为10 cm时，空心板应力最小；当铺装层厚度为15 cm时，空心板挠度最小。跨径L=16 m的空心板，铺装层厚度为6 cm时，空心板应力最小；当铺装层厚度为10 cm时，空心板挠度最小。跨径L=20 m的空心板，铺装层厚度为4 cm时，空心板应力最小；当铺装层厚度为6 cm时，空心板挠度最小。

3.4 理论最优厚度分析

标准跨径L分别为6 m、8 m、10 m、13 m、16 m和20 m时，应力最小和挠度最小时分别对应的铺装层理论最优厚度见表2。

表2 整体化铺装层理论最优厚度

取应力最小和挠度最小时所对应的整体化铺装层厚度的大值作为整体化铺装层的理论最优厚度，计算跨径和整体化铺装层理论最优厚度的关系曲线见图11。由图11可以看出，对于不同跨径的空心板桥，存在一种整体化铺装层理论最优厚度值使应力最小或挠度最小，理论最优厚度仅从结构出发，不考虑下部承载力和经济性。随跨径的增大，整体化铺装层理论最优厚度减小，跨径6 m空心板的整体化铺装层理论最优厚度为30 cm，跨径20 m空心板的整体化铺装层理论最优厚度减小为6 cm。

图11不同跨径下整体化铺装层理论最优厚度

4 考虑铺装层的叠合效应后空心板桥验算

对于某一固定跨径的装配式空心板梁桥，在原有旧桥的基础上，凿除原有破损的铺装层，加铺新的铺装层，原有空心板的高度是不变的，若铺装层的厚度太厚，桥梁承载能力不足，即桥梁在最不利组合情况下，空心板桥中至少有一个截面出现效应S大于抗力R的情况。

整体化铺装层可以提高结构的抗力R，改变结构的内力分担，降低结构的作用效应S，使得结构满足γ0S≤R。假设某一装配式空心板桥，仅将铺装层视为二期恒载作用于空心板桥上时的结构抗力是R1，作用在桥上的荷载组合效应为S，由于荷载作用效应的标准值提高，使得γ0S>R1，结构不满足承载力要求。若在空心板上浇筑整体化铺装层，在强度形成后，铺装层的结构抗力为R2，铺装层与空心板组合形成叠合结构，共同分担作用在桥上的荷载组合效应S。其中，空心板分担荷载作用效应S1，铺装层分担作用效应S2。若空心板满足γ0S1≤R1，同时铺装层满足γ0S2≤R2，则说明空心板与桥面铺装层都满足承载能力极限状态设计要求。

对跨径为6 m、8 m、10 m、13 m、16 m和20 m的空心板在整体化铺装层厚度分别为10 cm、20 cm、30 cm、40 cm时的承载能力极限状态正截面承载力和正常使用状态裂缝和挠度进行验算。

正截面承载力按式(3)计算。

(3)

式中：fcd为混凝土轴心抗压强度标准值；b为截面宽度；h0为截面有效高度，h0=h-a，h为截面全高，a为保护层厚度；x为受拉区高度。

裂缝宽度按式(4)～式(6)计算。

(4)

(5)

(6)

式中：C1为钢筋表明形状系数；C2为作用长期效应影响系数；C3为与构件受力性质有关的系数；ρ为纵向受拉钢筋配筋率，按式(5)计算；d为钢筋的直径；bf为构件受拉翼缘宽度；hf为构件受拉翼缘厚度；σss钢筋应力，按式(6)计算。

均布荷载作用下，构件的长期挠度值按式(7)计算。

(7)

式中：ηθ为挠度长期增长系数；B为开裂构件等效截面抗弯刚度。

可变荷载频遇值计算长期挠度值，按式(8)计算。

wQ=wl-wG

(8)

式中：wl为挠度长期值；wG为自重产生的挠度长期值。

承载能力极限状态正截面承载力和正常使用状态裂缝和挠度的验算结果见表3～表8。不同整体化铺装层厚度下各跨径空心板承载能力极限状态的验算和正常使用状态下均满足规范要求。在设计时，可根据桥梁跨径和结构要求，根据表3～表8中各数值，初拟整体化铺装层厚度。

表3 不同整体化铺装层厚度空心板验算(L=6 m)

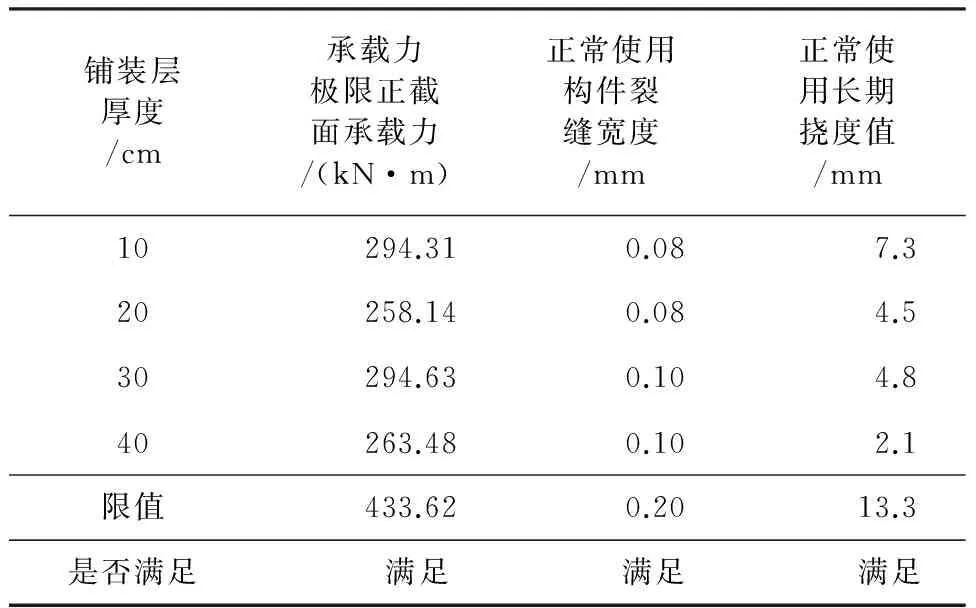
表4 不同整体化铺装层厚度L=8 m空心板验算

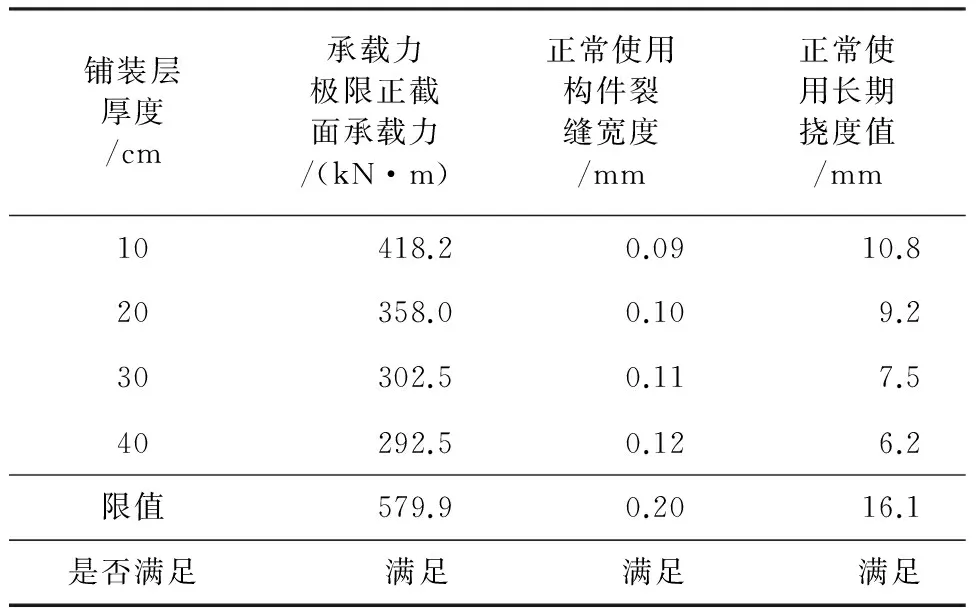
表5 不同整体化铺装层厚度L=10 m空心板验算

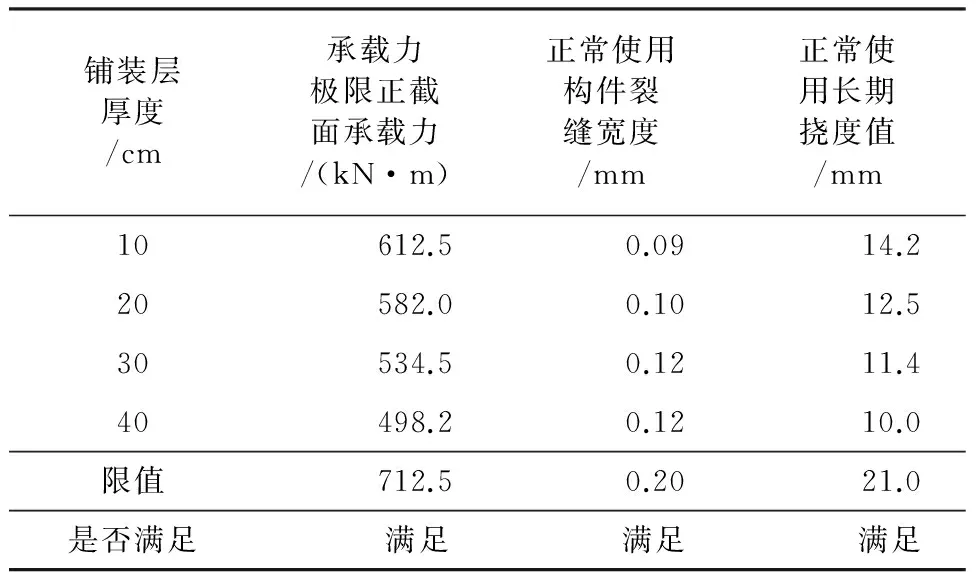
表6 不同整体化铺装层厚度L=13 m空心板验算

表7 不同整体化铺装层厚度L=16 m空心板验算

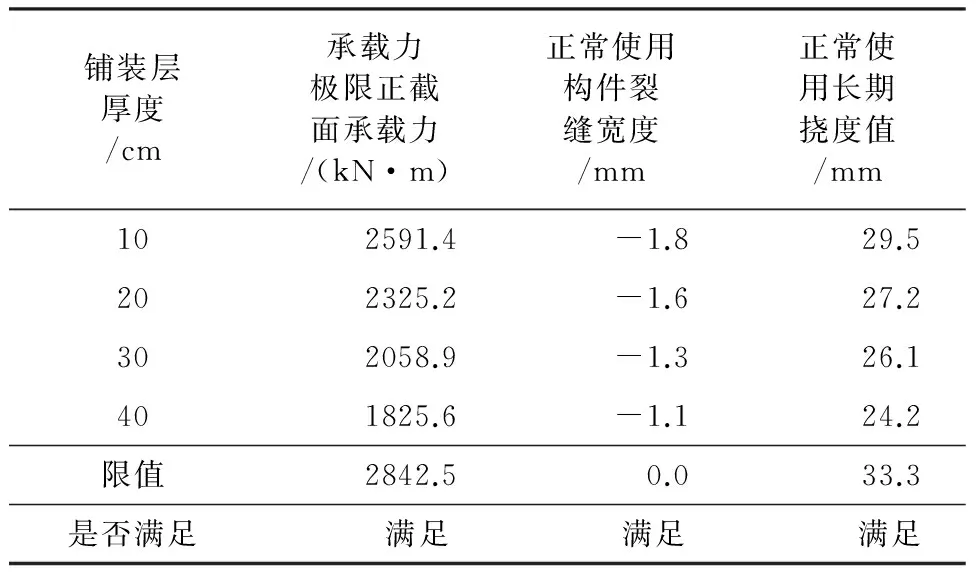
表8 不同铺装层厚度L=20 m空心板验算

5 结 语

(1) 整体化铺装层加固空心板受力可分为三个阶段，即空心板承受自重、空心板承受自重和整体化铺装层湿重、空心板与整体化铺装层共同承担外部荷载作用。

(2) 对于不同跨径的空心板桥，存在一种整体化铺装层理论最优厚度值使空心板跨中截面应力最小或挠度最小。

(3) 随跨径的增大，整体化铺装层理论最优厚度减小，当跨径从6 m增大到20 m，整体化铺装层理论最优厚度从30 cm减小到6 cm。

(4) 对不同跨径下不同整体化铺装层厚度的空心板梁进行承载力极限状态和正常使用极限状态验算，均满足要求。

参考文献：

[1] 许 莉，郑圣基.简支空心板桥车辆荷载效应分析[J].水利与建筑工程学报，2015，13(2)：7-10.

[2] 李增锋，庄一舟，程俊峰，等.装配式空心板斜交桥梁横向预应力的抗裂性能研究[J].水利与建筑工程学报，2017，15(5)：44-50，81.

[3] 李增锋，庄一舟，程俊峰，等.横向预应力对装配整体式空心板桥纵向抗裂性能的影响[J].水利与建筑工程学报，2017，15(3)：127-133.

[4] 王砚桐.高等级公路中“单板受力”现象及原因分析[J].公路交通技术，2004(4)：29-32.

[5] 陈宝春，陈友杰，赵 秋.桥梁工程[M].北京：人民交通出版社，2017.

[6] Seible F, Lathem C T. Analysis and design for structural concrete bridge deck overlays[J]. Journal of Structural Engineering，1990，116(10)：2711-2727.

[7] 鬲鹏飞.装配式箱梁桥整体化层合理厚度分析[D].西安：长安大学，2015.

[8] 郝宪武.装配式箱梁桥整体化层作用机理及其设计加固方法[D].西安：长安大学，2012.

[9] 商允福，陈广淳.预应力空心板桥超荷载设计方法[J].中国农村水利水电，2000(8)：40-41.

[10] 方 萍，万 水，叶见曙.钢桥面铺装力学特性试验研究[J].公路交通技术，2002(4)：7-11.

[11] 罗立峰，钟 鸣，黄成造.桥面铺装设计理论的研究[J].华南理工大学学报(自然科学版)，2002，30(4)：91-96.

[12] 徐洪涛.桥面铺装层的受力分析及承载力研究[D].天津：河北工业大学，2003.

[13] 唐国斌，项贻强，管品武.桥面铺装对中小跨径桥梁力学性能影响研究[J].公路交通科技，2010，27(12)：94-98，104.

[14] 邹兰林，彭 冬.装配式板桥桥面铺装层受力特性分析[J].公路与汽运，2010(5)：147-150.

[15] 吴颖恒，张俊平.桥面铺装对简支空心板桥受力行为的影响研究[J].广州大学学报(自然科学版)，2011，10(1)：60-64.

[16] 詹华熙，王国亮，魏洪昌.桥面补强层加固法系统研究[J].公路交通科技，2006，23(4)：87-90，103.

[17] 中华人民共和国住房和城乡建设部.混凝土结构设计规范：GB 5002—2010[S].北京：中国建筑工业出版社，2010.

[18] 刘 健.新老混凝土粘结的力学性能研究[D].大连：大连理工大学，2000.

[19] 刘沛林，时旭东，张天申.装配式钢筋混凝土简支板梁桥铰缝接触面应力分析[J].特种结构，2010，27(4)：77-80，84.

[20] 叶见曙，刘九生，俞 博，等.空心板混凝土铰缝抗剪性能试验研究[J].公路交通科技，2013，30(6)：33-39.

[21] 王 锋.桥面整体化铺装层加固空心板受力性能研究[D].福州：福州大学，2015.