多因素影响隧道仰拱竖向位移回归探析

宋 洋

(中铁二院工程集团有限责任公司，四川成都 610031)

近年来，随着我国高速铁路的大量兴建，深埋软岩隧道出现底鼓病害的情况越来越突出，尤其是隧道穿越具有微膨胀性的地层时，底鼓导致轨道板纵向位移超限等问题已引起工程界的重视，并开展了众多相关研究，取得了系列研究成果[1-4]。多年来，对于底鼓的研究大多针对软岩蠕变机理，且较多的研究是针对具体的工点。在实际隧道工程设计中，如何在众多蠕变本构中选择合适的模型来进行分析设计，一直是工程上的难题[5]。此外完备的岩体蠕变实验难以完成，对岩体蠕变参数的选择有诸多困难。故此时，通过软岩蠕变理论计算难以得到准确的隧道仰拱位移。因此，基于数值模拟得到的多因素仰拱竖向位移回归研究，具有重大的理论研究价值与工程指导意义。

本文以某高速铁路隧道为背景，通过数值试验研究模拟深埋软岩隧道底鼓，探索隧道仰拱在不同膨胀应力、不同仰拱矢跨比和不同衬砌厚度三个因素共同影响下的纵向位移规律，然后通过回归分析得到可接受的隧道底鼓预测模型。

1 工程背景

某铁路客运专线按照速度目标值250 km/h客运专线双线设计。隧道深埋段采用复合式衬砌结构(图1)，其中仰拱矢跨比设计为1/12，二次衬砌厚度为45 cm。隧道洞内采用CRTS-I型双块式无砟轨道。

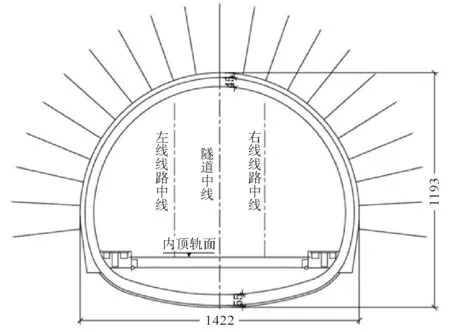
图1 复合式衬砌结构(单位:cm)

隧道围岩为三叠系下统铜街子组二段(T1t2)页岩，该页岩呈暗紫红色，泥质结构，判为IV级围岩，重度为21.5 kN/m3，弹性反力系数K为350 MPa。根据取样分析，页岩天然抗压强度24.3 MPa，饱和吸水率4 %，自由膨胀率6.9 %，膨胀应力50 kPa。

调试阶段进行轨道精测时，发现隧道K367+786～+837段(长51 m)无砟轨道的变形上拱，轨道板局部发现裂纹，仰拱上拱位移值达到5～15 mm(图2)。

图2 无砟轨道变形上拱示意

出现底鼓病害后，设计拟增大仰拱矢跨比和衬砌厚度，抵抗膨胀应力，抑制仰拱上拱。而膨胀应力、仰拱矢跨比和衬砌厚度三个因素决定了采取何种设计参数能够抑制底鼓。因此需要建立在围岩与结构多种因素影响下，快速预测仰拱纵向位移的数值模型。

2 数值模拟正交试验

本节通过正交试验原理，设计了在多因素影响下隧道底鼓正交试验，并结合工程背景建立荷载-结构模型，采用有限元计算得到膨胀应力、仰拱矢跨比、衬砌厚度与仰拱位移的对应数据。

本试验有三个自变量：q不同膨胀应力；f不同仰拱矢跨比；h不同衬砌厚度。根据工程背景，参考现行相关规范后，分别取25 kPa、40 kPa、50 kPa作为膨胀应力。选择较有代表的三种仰拱矢跨比，即1/12 、1/10、1/8。选择设计中IV、V级围岩常采用的3种二次衬砌厚度，即45 cm、50 cm、55 cm。

2.1 正交试验设计

正交试验设计是研究多因素、多水平试验的一种设计方法[6]。在试验研究中，常有多个自变量影响，正交试验设计可根据正交性挑选出有代表性的自变量组合进行试验，从而高效、快速、经济的完成研究[7-8]。

本试验可看做一个三因素三水平的试验，分别将不同膨胀应力、不同仰拱矢跨比、不同衬砌厚度对应为q、f、h三个因素，每个因素有三个水平，具体工况见表1。

表1 因素水平

每组试验各因素的具体水平组合可直接参考L9(34)正交表。

2.2 正交试验研究

在实际工程设计中，往往采用荷载—结构模型进行计算，此种计算方法得出的结果符合实际，且具有较强的操作性。首先建立几何模型，该隧道为双线隧道，二次衬砌轮廓为3心圆，净空宽度为12.8 m，净空高度为8.68 m。根据《隧道设计手册》，采用梁单元模拟二次衬砌，仰拱衬砌厚度较拱墙部位加厚10 cm，为了较好的模拟工程中的实际情况，过渡段采用厚度线性渐变的变截面梁单元模拟。根据TB 10003-2005《铁路隧道设计规范》，采用荷载-结构模型需考虑围岩对衬砌的约束作用，试验采用弹簧单元模拟这种弹性反力。在TB 10003-2005《铁路隧道设计规范》中，对深埋隧道荷载有细致的说明，本试验采取了规范中的计算方法，按工程背景和相关规范进行取值。计算中用到的参数如表2、表3所示。

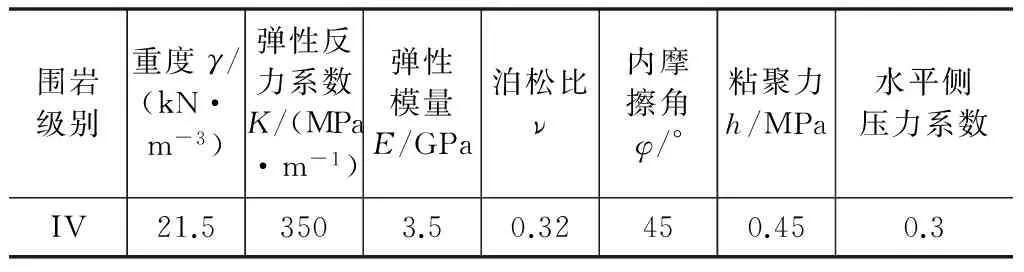
表2 围岩参数

一般的深埋隧道设计中，采用荷载-结构模型进行计算，仰拱受到的外力只有围岩弹性约束力，当隧道穿越具有弱膨胀性的地层时，还应当考虑地层的膨胀应力。膨胀应力具有各向异性，试验中采用匀部于仰拱的竖直向上荷载模拟。根据TB 10003-2005《铁路隧道设计规范》，复合式衬砌初期支护按主要承载结构计算，因此分担到二次衬砌的荷载均按80 %考虑。荷载—结构计算模型如图3所示。

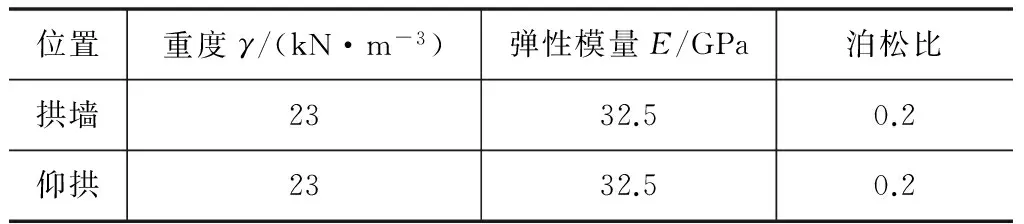
表3 二次衬砌参数取值

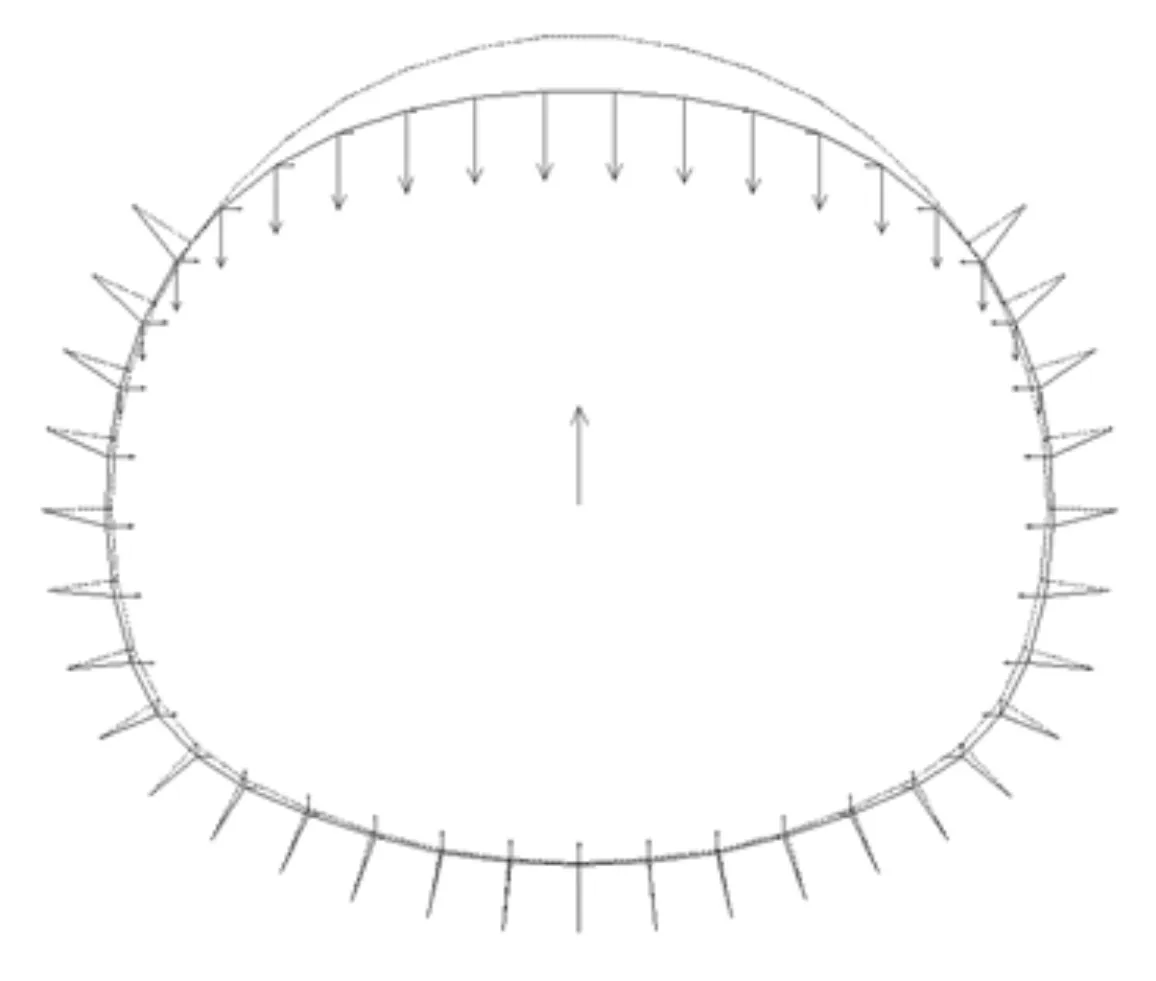
图3 计算模型

在荷载—结构模型计算中，由于采用有限元方法，同一种几何模型在不同的单元划分情况下得到的计算结果有差异，因此在本研究的9组试验中，每组试验采用3种不同的单元划分，共计27个计算工况。

2.3 正交试验结果

采用ANSYS对上述27个荷载—结构模型进行求解，提取仰拱纵向位移如表4。

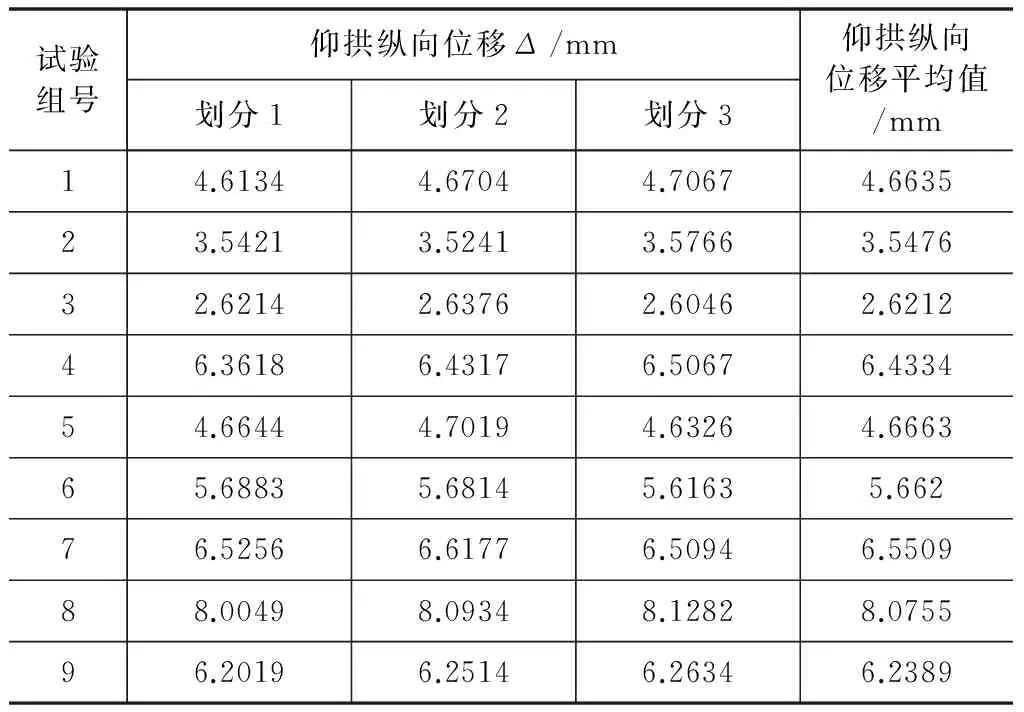
表4 仰拱纵向位移

从表4中可以看出，荷载—结构模型计算出的仰拱纵向位移与现场仰拱纵向位移差距不大，因此采用荷载—结构模拟底鼓病害是可行的。

3 正交试验结果分析

通过上一节的正交试验研究，得到27组试验因素q、f、h与仰拱位移Δ的对应数据，本节先将数据进行归一化处理，然后通过拱的挠度理论建立合理的回归方程，再进行回归分析，得出各因素与仰拱位移率Δ′的定量关系。

3.1 试验数据归一化处理

为了使试验结果具有普遍性，对试验中的变量数据进行了无量纲化处理。无量纲化的手段多种多样，本文采用了常见的归一化处理，即选定一个与变量同量纲的标准值，求出二者比值作为无量纲变量。

首先选定一种环境作为基准环境，膨胀应力采取25 kPa作为基准，仰拱矢跨比采取1/12为基准，衬砌厚度则采用IV级围岩衬砌常用的厚度45 cm为基准。对试验中的三个因素：膨胀应力、衬砌厚度、仰拱矢跨比进行归一化，采用各水平膨胀应力与25 kPa的比值作为膨胀应力的无量纲水平，记作q，25 kPa、40 kPa、50 kPa分别对应1、1.6、2；采用各水平与1/12的比值作为仰拱矢跨比无量纲水平，记作f；采用各水平与45 mm的比值做为衬砌厚度无量纲水平，记作h，45 cm、50 cm、55 cm分别对应1、1.25、1.375。

本次试验的结果指标设计为仰拱位移率Δ′，即各实验组仰拱位移Δi与基准环境下仰拱位移Δ0之比

(1)

根据上一节的试验结果，可计算出仰拱位移率Δ′(表5)。

表5 仰拱位移率统计

3.2 建立回归模型[9]

将仰拱视为无铰拱(图4):

图4 无铰拱计算示意

由虚功原理：

(2)

可以得出无铰拱拱顶位移:

(3)

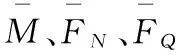
对式(3)第一项进行分析，在边界条件为对称竖向荷载的情况，可以得到：

(4)

由于是圆弧拱，y=R(1-cosθ)，x=Rsinθ

根据几何关系，矢跨比：

(5)

由三角函数关系可知：

(6)

同理可得：

(7)

故：

(8)

3.3 多元回归分析[10]

令：

则仰拱位移率Δ′与8个变换后的量ai,bi,ci,di,ei,fi,gi,hi存在线性关系(表6):

k7gi+k8hi+ei，i=1,2,…,9

(9)

可得正规方程式的矩阵形式为：

(XTX)k=XTΔ′

(10)

或：

Ak=B

(11)

式中：k=(k1,k2,k3,k4,k5,k6,k7,k8)为正规方程中待定的未知实数向量， 如果系数矩阵A满秩， 则A-1存在，

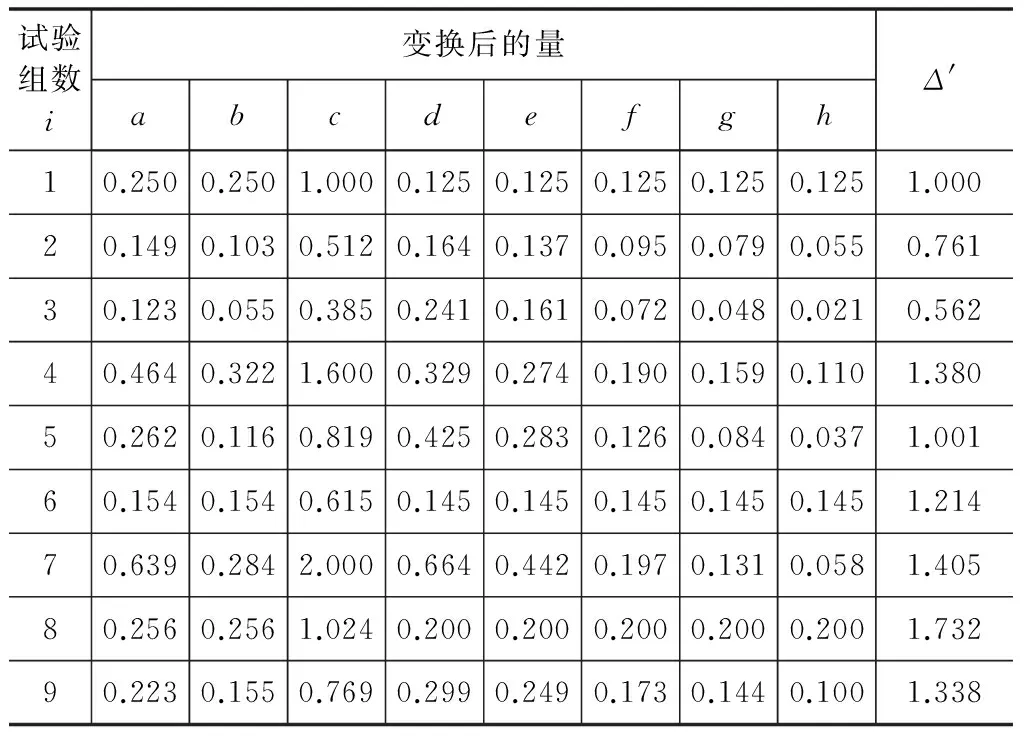
表6 试验观测数据

此时有：

k=A-1B=(XTX)-1XTΔ′

(12)

通过以上方法，解出各系数，得到多元回归模型为：

(13)

该回归模型表明，膨胀应力、仰拱矢跨比、衬砌厚度对仰拱纵向位移均有显著影响，且仰拱纵向位移与膨胀应力呈正相关；与衬砌厚度倒数呈正相关；与仰拱矢跨比呈复杂的非线性关系。

4 回归模型验证

本研究设置4个检验组，通过对比检验组荷载-结构计算的Δ′与回归模型计算的Δ′，验证回归模型可靠度。选择70 kPa、100 kPa作为检验组膨胀应力。选择1/6 、1/5作为检验组仰拱矢跨比。选择50 cm、55 cm作为检验组二次衬砌厚度。检验指标依然为仰拱位移率Δ′，即各检验组仰拱位移Δi与基准环境下仰拱位移Δ0之比。检验组的设置和回归验证如表7所示。

可以看到，检验组中模型计算Δ′与回归计算Δ′的误差较小，可以认为回归模型具有统计意义，能够快速地预测在围岩与结构多种因素影响下，仰拱纵向位移。

5 结论

(1)采用正交试验方法，研究在围岩与结构多种因素影响下隧道仰拱纵向位移的规律是可行的；通过荷载—结构模型计算出的仰拱纵向位移与现场仰拱纵向位移差距不大，采用荷载—结构模拟底鼓病害是可行的。

表7 回归验证统计

(2)通过理论分析，建立仰拱位移率Δ′与因素q膨胀应力、f仰拱矢跨比、h衬砌厚度的关系模型，将正交试验得到的数据进行回归分析，得到的多元回归模型表明，膨胀应力、仰拱矢跨比、衬砌厚度对仰拱纵向位移均有显著影响。

(3)通过设置检验组进行对比，验证多元回归模型的可靠度，结果表明回归模型具有统计意义，能够快速地预测仰拱纵向位移。

[1] 张良刚.特大断面板岩隧道围岩变形特征及控制技术研究 [D]. 中国地质大学, 2014.

[2] 李廷春.毛羽山隧道高地应力软岩大变形施工控制技术 [J]. 现代隧道技术, 2011 (2).

[3] 李建军,张志强.岩石蠕变对隧道二次衬砌结构影响的研究 [J]. 现代隧道技术, 2011 (6).

[4] 吕志涛,吴庚林,靳晓光,等.隧道膨胀性围岩蠕变特性分析及参数反演 [J]. 地下空间与工程学报, 2016 (6).

[5] 焦春茂.岩体非定常流变模型的有限元计算及位移反分析 [D]. 山东科技大学, 2005.

[6] 董如何,肖必华,方永水.正交试验设计的理论分析方法及应用 [J]. 安徽建筑工业学院学报(自然科学版), 2004 (6).

[7] 张志强,何本国,李永珑,等. 节理岩体隧道稳定性影响因素正交试验及锚杆作用要点研究[J]. 武汉理工大学学报,2013(2).

[8] 苏永华,李翔,丁云,等. 基于二次正交试验优化的隧道围岩稳定可靠度方法 [J]. 岩土工程学报, 2012 (2).

[9] 龙驭球,包世华.结构力学 [M].北京: 高等教育出版社.

[10] 德格奥特. 概率论与数理统计 [M].北京: 高等教育出版社.