大学城内智能快递柜服务网点选址研究—以郑州市龙子湖大学城为例

（郑州大学 管理工程学院，河南 郑州 450000）

1 引言

迄今为止，我国已建成大学城60余座[1]，如：南京仙林大学城、广州大学城、郑州龙子湖大学城等。大学的聚集分布有利于充分利用高校园区丰富的资源，实现优势互补，发挥高校园区整体优势[2]。大学生作为网购的重要群体，消费规模不断扩大。大学城内快递数量急剧增加，校园快递末端配送效率低下的问题日益凸显。研究表明，智能快递柜的使用减少了学生等待时间，方便寄取快递，有效解决快递“最后一公里”问题[3-5]。大学城内智能快递柜的使用群体不仅限于本大学师生，如果智能快递柜服务网点的位置选择得当，可以满足多个大学学生的共同使用，从而服务更多学生群体，提高快递的服务效率和学生取件的便利性。

目前，已经有学者对智能快递服务网点的推广使用进行研究探讨。如：杨士涓[6]从智能快递柜基于微信公众平台的信息服务、多方合作校企商业模式、创新运作模式等方面进行了分析。朱溪亭[7]提出构建基于智能快递柜的校园快递服务点，整合校园快递终端业务从而提高校园快递服务水平。张秋燕[8]分析了智能快递自提柜的发展现状并与传统快递自提模式进行了对比，为亚马逊成功运用智能快递自提柜提供了建议。任为[9]分析得出智能快递柜在发展过程中存在着商业运营模式不清晰、投放空间不灵活、布置受限、恶性竞争和增值服务欠缺的问题，并提出了针对性的应对策略，如快递公司自投快递柜、智能快递柜与传统派送相结合、统一规划布局和推广增值性服务。孙红、周帆[10]等就智能快递柜发展过程中存在的问题进行研究，提出了完善智能快递柜服务系统的方法。

目前对选址规划问题进行研究有以下几种方式。一是定性研究，利用专家打分法或者德尔菲法对选址位置进行研究。二是采用双层规划模型、多目标选址模型、集合覆盖模型等结合人工智能算法进行选址优化研究[11]。目前，采用后者进行选址研究的学者居多。如：王勇[12]以运输费用和建设成本最小为目标基于改进蚁群算法将配送中心选址阶段看成聚类问题，将已经分配了供货点的候选配送中心作为聚类中心，求出配送成本最低的配送方案，从而对多物流配送中心进行选址。周翔[13]等构建了配送中心和末端节点的两阶段布局模型，以取货距离、配送时长为主要考虑因素建立了顾客满意度函数，采用中心偏移二次聚类算法解决末端节点的数量及规模。

在智能快递柜网点选址方面，施书彪、黄有方[14]以租金成本、配送成本和惩罚成本最小化为目标建立了校园智能快递柜选址模型，并以实例验证了模型的可行性。冯斌[15]利用K-mean法对选址区域进行分区，降低了选址的难度，建立了智能快递柜备选址评估指标模型，应用AHP法和模糊综合评价法确定了备选址的位置，应用0-1整数规划和排队论模型确定了智能快递柜的精确选址和选址规模。王嘉琦和邹恩[16]指出国内的智能快递柜运营模式主要有电商企业自建自用、快递企业自建自用和第三方平台共用三种，目前尚处于企业自发创新的初期阶段。丁猛[17]采用覆盖模型方法，以网点数量最小和固定网点数量为目标，以各需求点取件距离之和最短为约束条件建立高校智能快递柜网点选址模型。李玉民、杨露[18]等认为第三方平台共用模式是目前最普遍的智能快递柜运营模式，并基于演化博弈理论构建了快递企业和第三方智能快递柜企业之间的演化博弈模型。

与我国相比，国外针对快递“最后一公里”终端配送设备的研究已经达到了一定的水平，其理论和实践都相对成熟[19]。其中，快递自提服务主要存在于日本和中国台湾、欧洲等地，如日本和台湾的“便利店提货模式”、新加坡的第二代自助式邮亭、欧洲的“收寄点（CDP）”等[15]。目前，国外关于智能快递柜的研究主要集中于有人值守式CDP和无人值守式CDP两种。Rowlands[20]和Esser[21]分别介绍了CDP在英国以及德国的发展趋势，通过实证研究证明了CDP的使用率和在顾客中的认知率均呈现逐步上升趋势。Weltevreden[22]分析了荷兰消费者的网购数据，揭示了自提点对零售企业、购物中心和消费者的影响程度。Rowlands[20]综合考虑递送成本、递送时效、投资开发回收期等多方面因素，细致地比较分析“无人交付接收盒”和“递送盒”的应用范围和应用区别，研究发展在人群集中区域投放“无人交付接收盒”更能够节省运输成本，提高投资收益。Michael[23]通过比较分析，得出有人值守式CDP在快递末端配送上具有较大的发展优势，并进一步介绍了有人值守式CDP的未来发展前景。

本文拟从时间方面对大学城内智能快递柜服务网点布局进行优化，寻找大学城内网点个数最少的布局方式。将时间参数转化为距离参数，以此确定智能快递柜服务网点的辐射半径，构建大学城内智能快递柜服务网点布局的集合覆盖模型，利用集合覆盖的启发式算法进行求解，进而得到最优网络布局方式，旨在提高学生取件效率，降低企业建设成本。

2 问题描述

大学城内物流快递系统主要包括以下几个部分：快递分拨中心、配送中心和快递服务网点。其中，学生取件的便利性和快递服务网点的性质和选址点紧密相连。智能快递柜的使用减少了学生等待时间，方便寄取快递。本文提出在大学城内建设智能快递柜服务网点，并对大学城内网点进行选址分析，以解决大学城内高校学生快件收发问题，即大学城内快递“最后一公里问题”。通过建立智能快递柜服务网点，为学生群体提供更加便利、快捷的服务，解决学生群体取件难、取件时间长的问题，同时增加企业的效益。本文就智能快递柜服务网点布局问题进行研究。

智能快递柜服务网点候选点集合为{j|j∈J,j=1,2,…,m}，需求区域（学生宿舍群体）集合为{i|i∈I,i=1,2,…,n}。假设候选点个数若干，每个网点的服务能力用网点容量来表示，则需求服务匹配存在3种情况：若dij＞L，服务网点候选点将不对该需求点进行服务；若dij≤L且未超过网点服务能力，服务网点候选点将对该需求点进行服务；若dij≤L但超过网点服务能力，则不对该需求点进行服务。其中L为网络服务网点候选点的辐射半径，dij为服务网点候选点到学生群体需求点的距离。智能快递柜服务网点布局示意图如图1所示。

图1 智能快递柜服务网点布局示意图

3 模型设计

3.1 模型假设

由于大学城内智能快递柜服务网点的容量和辐射半径选择范围较大，服务对象学生群体对于取件具有很强的时间约束，建设智能快递柜服务网点用地存在不确定性。对此，对大学城内智能快递柜服务网点选址过程中有关参数进行如下说明：

（1）快递件单位化处理。由于智能快递柜本身包含大中小3种不同类型的格子，在此我们只考虑快递件数量，不考虑快递件的大小和形状。

（2）需求点的确定。大学城不同于一所大学，学生需求点不应按照单栋学生宿舍进行划分。高校内学生群体通常的活动范围都在宿舍、食堂、教学楼和图书馆之间。一般高校园区内宿舍群周围都附带有商业街以满足学生生活的日常需求。故本文只考虑学生活动范围在宿舍周围。将大学城内的半径100m内的宿舍区域看作一个需求点。

（3）智能快递柜服务网点的处理量。智能快递柜服务网点的处理量与其覆盖半径和其覆盖区域内学生数量有关。理论上，网点的覆盖半径越大，学生数量越多，其处理量就越大。但结合实际情况，由于智能快递柜服务网点的数量限制，不同辐射半径和学生密度对应1个最佳处理量，避免智能快递柜服务网点容量闲置造成浪费。

（4）智能快递柜服务网点覆盖半径。一般来说，在学生步行速度一定的情况下，需求点与网点之间距离越短，取件时间就越短。为保证学生取件的最大便捷性，按照步行5km/h，10min内取得快递，则智能快递柜服务网点覆盖半径最大应为800m。

在对大学城内学生取件问题描述和参数设置的基础上构建集合覆盖模型，以实现智能快递柜服务网点布局，提出如下假设：

假设1：假设建立一个智能快递柜服务网点的固定成本相同。

假设2：不考虑狂欢购物节对大学城内快递数量的影响。

假设3：不考虑其他竞争企业对设立智能快递柜服务网点的影响。

假设4：不考虑区域内交通影响因素，设定所有网点的最大服务半经上限一致。

3.2 模型建立

基于以上假设及大学城内智能快递柜服务网点的特点，建立大学城内智能快递柜服务网点选址的集合覆盖模型。建立最大覆盖模型的目标是在最大服务半径确定的情况下对有限的服务网点进行选址，满足尽可能多的需求点。

式（1）中，sj为智能快递柜服务网点选址变量，N为学生群体需求区域i的集合，N={1,2,…,n}。当sj=1时，表示备选点j作为智能快递柜服务网点选址点。当sj=0时，表示备选点j不被作为智能快递柜服务网点选址点。为保证1个地方最多只能投建1个网点，sj应满足：

式（2）中，M为智能快递柜服务网点备选网点j的集合，M={1,2,…,m} 。需求点i到备选点j之间的距离dij表示为：

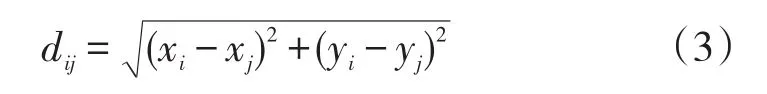
每个服务网点的覆盖半径是有限的，只有当学生需求点在服务网点的覆盖范围内，智能快递柜服务网点才对此需求点进行服务，并且允许1个服务网点只提供部分需求，同时保证每个需求点快递处理量得到满足，因此yij应满足：

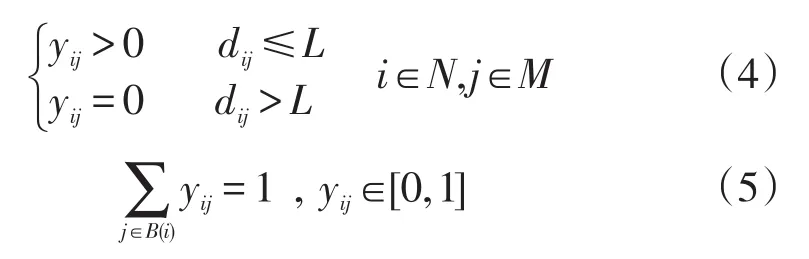
式（4）、式（5）中，y′ij为服务网点j满足需求点i需求量的百分比；L为网点的覆盖半径；B(i)为覆盖需求点i的网点j的集合。当yij=0，表示需求点i的需求量未分配给网点j；当0＜yij≤1，表示需求点i的需求量被分配给网点j，且被分配的需求量百分比为yij。每个网点都有其最大处理量，超过最大处理量则不能继续进行服务，因此需要对每个网点的服务能力进行限制，其约束条件为：

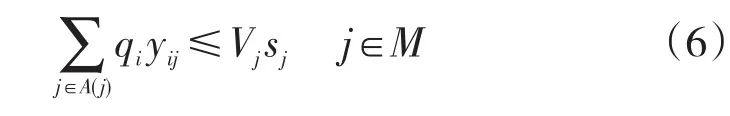
式（6）中：qi为需求点i的需求量；Vj为智能快递柜服务网点的处理量；A(j)为网点j所覆盖的需求点i的集合。

3.3 模型求解

集合覆盖问题属于NP-hard问题，不存在多项式求解算法。这类问题的求解方法主要分为两大类：一是枚举法，能够找到小规模问题的最优解，但对于规模较大的问题无法有效求解[24]；二是启发式算法，比如遗传算法、人工神经网络算法、蚁群算法、模拟退火算法等，所得结果不能保证是全局最优解，但可保证是可行解，可对大型问题有效分析、求解[25-26]。本文选择一个集合覆盖的启发式算法[27]，主要步骤如下：

第一步：初始化。令所有的yij=0，sj=0，，并确定集合A(j)和集合B(i)。

第二步：选择下一个服务网点。在M中选择sj=0且当A(j)的模为最大时，点j′为网络节点，即|A(j)|=max{|A(j)|,j∈M} ，令sj=1，并在集合M中提出节点j′，即M=M{j′}。

第三步：确定节点j′的覆盖半径。将A(j)中的元素按B(i)的模从小到大的顺序指派给j′，直至j′的处理量为Vj=0 或A(j)为空。其中，对于i∈A(j′)且yi＜1，将i指派给j′的方法为：若qi(1-yi)≤Vj，则令yij=1-yi，Vj=Vj-qi(1-yi)，yi=1在A(j)和N中剔除 需 求 点i。 若qi(1-yi)≤qj，则 令yij=Vj′/qi，

第四步：若N或M为空，停止；否则，更新集合A(j)和B(i)，转第二步，直至N或M为空。

运用Matlab2014进行编程求解，得到智能快递柜服务网点的最小个数及布局方式，并将此时服务网点的处理能力设为建设容量。

3.4 方案评价

由于选址问题是一项复杂系统，在对方案进行选择时需要考虑多方面的因素。因此，对于方案的评价本文从企业和学生两方面进行考虑，采用综合打分法对方案进行选择。对学生便利性而言，大学城内智能快递柜服务网点选址对学生取件主要影响因素有取件距离远近，距离越近对学生便利性越大。由于覆盖模型选址已确定好其辐射半径，因此本文可以将距离因素转化到学生需要跨校取件数量多少，需要跨校取件的快递数量越多，此方案对学生便利性越差。对企业成本而言，大学城内智能快递柜服务网点选址主要与网点数量有关。网点数量越多，企业的建设成本配送成本就会越高。本文建立一个综合打分模型对不同方案进行评价。

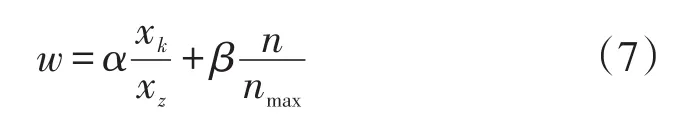
式（7）中：w为方案评价得分，xk为大学城内学生跨校取件的数量，xz为大学城内快递件总数，n为当前方案中智能快递柜网点的个数，nmax为所有方案中智能快递柜服务网点的个数最大值，α为学生便利性的影响因子，β为企业成本大小影响因子，w值最小的备选方案为智能快递柜服务网点最优选址方案。

4 算例分析

为验证本文大学城智能快递柜服务网点选址模型和算法的有效性，本文以郑州龙子湖大学城作为案例进行分析。龙子湖大学城内有15所高校，河南大学龙子湖校区等高校还未投入使用，本文仅以环龙子湖路的12所高校作为研究对象。关于龙子湖大学城具体院校情况及在校生数量见表1。

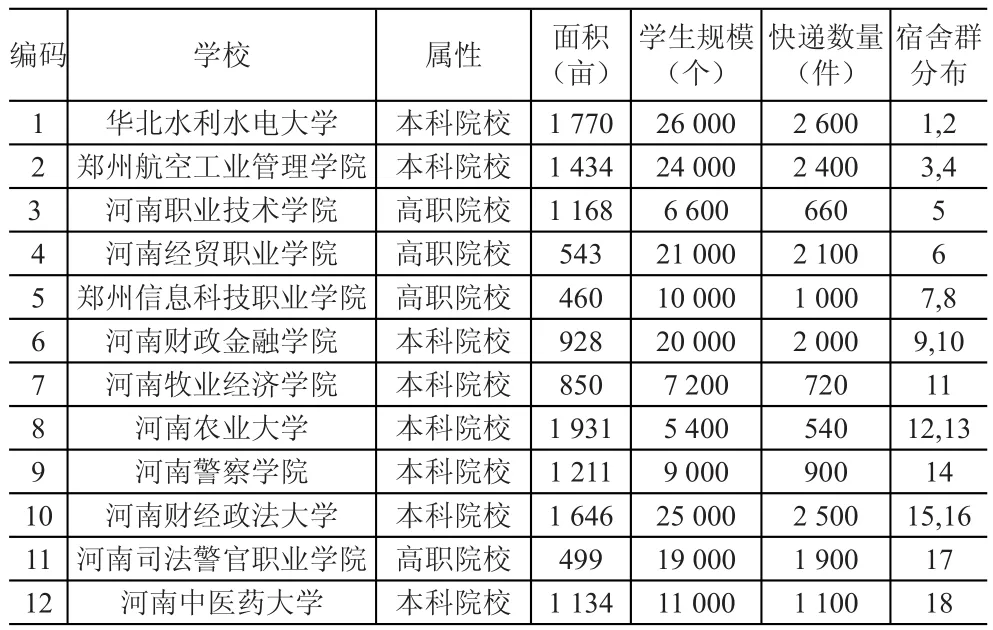
表1 龙子湖高校园区学校基本数据情况

本文选取龙子湖大学城内12所高校内的18个宿舍群作为智能快递柜服务网点的需求点，并为每个需求点进行编号，以1：400的比例绘制在12cm×12cm的区域内得到其坐标位置(x,y)。各学生宿舍群需求点坐标(x,y)和快递数量q情况见表2。关于大学城学生快递数量，只考虑智能快递服务网点快递柜存储格子数量满足学生日常快递件数量。根据调查，平日高校快递数量为高校人数的10%。对于一所高校有两个或多个需求点的情况，按照需求点所包含宿舍数量比例对快递数量进行分配，为该需求点的需求量。

表2 学生宿舍需求点坐标及需求量

大学城内学生群体通常的活动范围都在宿舍、食堂、教学楼和图书馆之间。一般高校校园内宿舍群周围都附带有商业街以满足学生生活的日常需求。基于此，考虑到学生跨校取件还是存在不便，选取分布在龙子湖大学城内12所高校的12个初始点作为智能快递柜服务网点的初始位置。表3表示了12个候选网点的位置(x,y)以及拟建网点的初始处理量V。

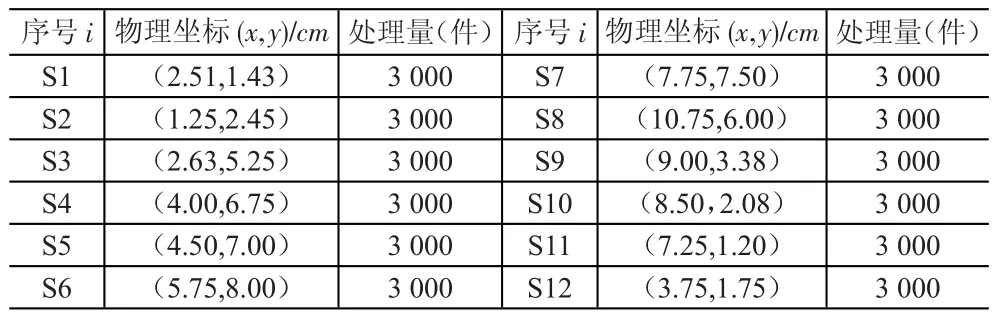
表3 候选服务网点的坐标及拟建网点的初始容量

根据学生群体对时效性的要求，为保证学生取件的最大便捷性，按照步行5km/h，10min内取得快递，则智能快递柜服务网点覆盖半径最大应为800m。即智能快递柜服务网点覆盖半径可控制在200-800m，因此，映射在12cm×12cm的区域内L的取值控制为0.5-2cm，以每200m为单位将网点辐射半径L分为1、1.5、2cm三种情况，处理量V以每3 000为单位设置为3 000、6 000个快递柜格子2种情况。以此构成6（3×2）种不同情况的组合，构建集合覆盖模型，运用算法求解，运行Matlab得到L=1cm，V=3 000（件）时的网络布局方式，如图2所示。

图2 覆盖半径为1cm，容量为3 000件时的网络布局方式

在给出的12个候选网点中，选出12个节点位置作为智能快递柜服务网点位置，即龙子湖大学城内每所高校建设一个智能快递柜服务网点。网点处理能力分别为1 715、2 400、660、100、3 000、2 000、720、540、900、1 500、2 900、1 985件。其中需求点1的快递数量由网点1和12各满足50%；需求点8的快递数量由网点4满足20%，网点5满足80%；需求点18的快递数量由网点10和11各满足50%。同理，将6种情况依次进行求解，结果见表4。

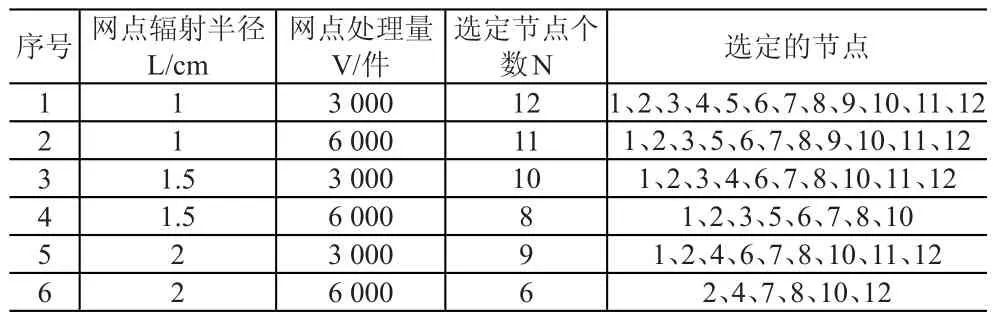
表4 不同网点辐射半径L和处理量V的网络布局方式

分析网点的辐射半径、处理量和节点个数之间的关系。可知，当网点辐射半径保持不变，随着网点容量的增加，选中的网点个数逐渐减少。当网点容量保持不变，随着辐射半径的增加，选中的网点个数逐渐减少。当网点个数最少时，随着网点容量的增加，网点容量利用率逐渐下降。

运用综合打分法在6种方案中选出最佳方案，假设α=0.6，β=0.4，计算可得6种方案的得分依次为0.465,0.496,0.495,0.526,0.576,0.524。故应选择方案1，即网点辐射半径为400m，网点容量为3 000件的方案，此时12个规划网点全部为建设网点，建设网点的处理件数分别为1 715、2 400、660、100、3 000、2 000、720、540、900、1 500、2 900、1 985件。网络布局方式如图2所示，智能快递柜选址节点及分配需求见表5。

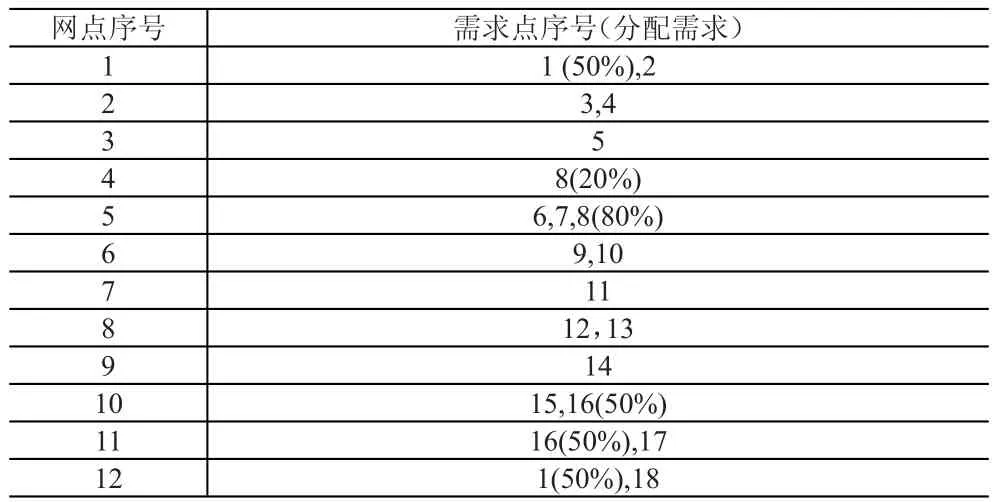
表5 龙子湖大学城智能快递柜选址节点及分配需求

5 结论

本文研究大学城内智能快递柜服务网点的选址布局，建立了以网点个数最少为目标，网点辐射半径和容量作为约束的集合覆盖模型，求解分析并确定候选方案；同时考虑学生取件便利性及企业建设成本问题，运用综合打分法找到最理想的网点布局方案，确保大学城内所有学生宿舍需求点都被网点覆盖，以布局和优化智能快递柜服务网点。计算结果得到，最优方案为方案1，即以网点辐射半径为400m，网点容量为3 000件在龙子湖大学城12所高校内每个高校建设一个智能快递柜服务网点。计算结果与实际相符。

[参考文献]

[1]李翠.大学城教育资源共享分析—以济南长清大学城为例[D].济南:山东经济学院,2011.

[2]姜同仁,马向文,王亚飞,等.集约化高校园区体育教育资源与开放式教学模式构建[J].武汉体育学院学报,2011,(3).

[3]罗明,陈勇.智能自提柜应对电商物流“最后一公里”的对策研究[J].物流技术,2016,35(5):22-24.

[4]刘玫“.快递自提柜”解决最后一公里的难题[J].科技视界,2015,(28):185.

[5]王凤美.谈最后一公里的智能化解决方案—智能快递柜[J].物流工程与管理,2016,38(6):67-68.

[6]杨士涓,顾淑红.高校校园快递发展及智能快递柜的应用与推广—以广西师范大学为例[J].物流技术,2017,36(5):154-157.

[7]朱溪亭.基于智能快递柜的校园快递终端业务整合研究—以苏州健雄职业技术学院为例[J].中国商论,2015,(27):87-89.

[8]张燕秋.关于智能快递自提柜的研究及应用分析—以亚马逊为例[J].科技广场,2014,(10).

[9]任为.浅议智能快递柜发展的制约因素及策略[J].中小企业管理与科技旬刊,2015,(20):187-187.

[10]孙红,周帆,刘玉博,等.智能自助快递柜的应用及发展方向[J].科技传播,2016,8(5).

[11]陈义友,陈以衡.基于逐渐覆盖的自提点选址模型与算法研究[J].计算机应用研究,2016,(8):1-5.

[12]王勇,何宇.基于改进蚁群算法的多物流配送中心选址[J].经营管理者,2011,(2):281-298.

[13]周翔,许茂增,吕奇光.B2C模式下配送中心与末端节点的两阶段布局优化模型[J].计算机集成制造系统,2014,20(12):235-259.

[14]施书彪,黄有方,严伟.智能柜在校园快递配送中的应用研究[J].计算机仿真,2015,32(9):421-424.

[15]冯斌.智能快件箱布局规划与运营模式研究[D].北京:北京交通大学,2015.

[16]王嘉琦,邹恩.基于智能快递柜模式的网购末端物流应用分析[J].物流技术,2015,34(5):58-60.

[17]丁猛.大学校园智能快递柜选址研究[D].深圳:深圳大学,2016.

[18]李玉民,杨露,王新露,等.快递与第三方智能快递柜合作机制的演化博弈分析[J].郑州大学学报(工学版),2017,(5):81-85.

[19]刘立华.智能快递柜自助服务的应用及其发展方向[J].物流工程与管理,2015,37(8):54-55

[20]Xu J,Jiang L,Wang S.Construction of Pick-Up Points in China E-commerce Logistics[A].Proceedings of the 2012 International Conference on Cybernetics and Informatics[C].New York:Springer,2014.

[21]Esser K,Kurte J.B2C E-Commerce:Impact on Transport in Urban Areas[A].Recent Advances in City Logistics.The 4th International Conference on City Logistics[C].2006.

[22]Weltevreden J W J.B2C e-commerce logistics:the rise of collection and delivery points in The Netherlands[J].International Journal of Retail&Distribution Management,2008,36(8):638-660.

[23]Browne M,Anderson S,Allen J,et al.Overview of home deliveries in the UK[Z].2001.

[24]王继强.集合覆盖问题的模型与算法[J].计算机工程与应用,2013,49(17):15-17.

[25]毕娅,李文峰.基于约束的覆盖选址分配问题[J].上海交通大学学报,2013,47(3):495-499.

[26]赵霞,窦建平.求解农产品供应链网络设计问题的混合粒子群算法[J].管理工程学报,2013,27(4):169-177.

[27]李玉民,王新露,郭晓燕.基于集合覆盖模型的农产品冷链网络布局[J].中国农业大学学报,2017,22(9):212-220.