一种具有分段曲率补偿的带隙基准电路

秦晋豫 ，吕 坚 ，周 云 ，阙隆成 ，田 雷

（1.电子科技大学光电科学与工程学院，成都610054;2.中国电子科技集团公司第四十九研究所，哈尔滨150009）

1 引言

随着深亚微米集成电路技术的不断发展，芯片集成规模越来越大，为了保证整体系统的正常工作，带隙基准源的精度起着至关重要的作用，它的温度特性直接决定了整体电路的精度和性能。而传统的带隙基准源通常采用一阶的补偿方法，其温度系数在20～100ppm/℃，传统的带隙基准无论在精度、稳定性，还是在功耗上，都远远无法满足现在微电子系统的需求。因此，提高带隙基准源的精度是十分重要的[1－3]。

针对传统带隙基准源的问题，已经有很多人提出了曲率补偿的办法。文献[4]用具有不同温度特性的电阻对基准源进行曲率校正，但是过分依赖于电阻的温度特性，对工艺要求较高。文献[5]提出一种低压曲率补偿基准电压源，但是该电路使用的晶体管多，结构复杂。文献[6]提出一种具有高的PSRR的曲率补偿电路，但是该补偿电路经过曲率补偿后，精度提升小，电路结构复杂，极大地增加了系统的功耗。采用分段曲率补偿技术在传统Borkaw带隙基准源的结构上进行改进，对带隙基准电压温度特性曲线在高、低温段进行曲率补偿，得到一种结构简单、功耗低、具有高精度的温度特性的基准源。

2 传统带隙基准源结构和原理

双极晶体管的基极—发射极电压（PN结二极管）的正向电压VBE具有负温度特性。室温下，有两个双极晶体管工作在不相等的电流密度下，它们基极－发射极电压的差值就与绝对温度成正比其中两个双极晶体管电流密度之比为n/1[7]。利用得到的正、负温度系数电压，可以得到一个零温度系数的基准电压将该式对温度求导，选择适当的系数K，使求导值在特定的温度下为0，从而得到零温度系数的基准电压。

基于上述原理，已经有很多经典的带隙基准电路产生，其中传统Brokaw结构的具有较好的温度特性温度。传统的Brokaw结构示意图如图1所示。

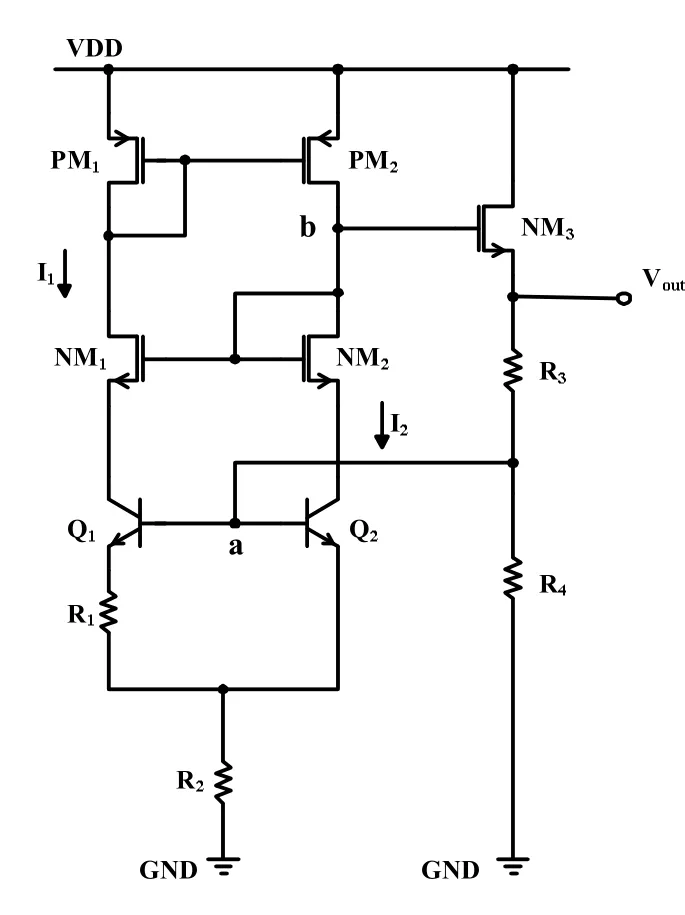
图1 传统Brokaw带隙基准结构示意图

Borkaw带隙基准电压源是1974年由A.Paul Brokaw在Widlar带隙基准电压源的基础上提出来的。与Widlar带隙基准电压源相比较而言，Brokaw基准可以产生两倍的PTAT电流，减小了Q1和Q2大的发射区面积比所带来的器件失配，具有更好的电压温度特性[8－9]。如图 1 所示，PM1、PM2和 NM1、NM2构成电流镜，产生与电源无关的偏置，保证流过Q1和Q2的电流其中，所以两倍的正温度电流I1流过R2产生正温度系数电压可以得到基准电压为：

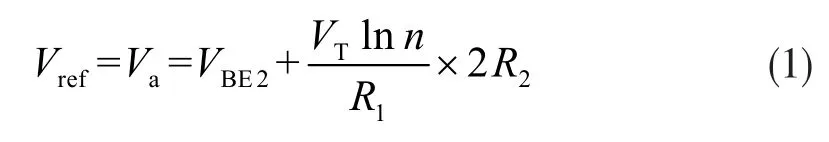
将上式对温度求导，并在室温下令等式结果为零，就可以确定出所需的R2和R1的比值，从而得到室温下温度系数为零的参考电压。

由图2的传统带隙基准结构的仿真结果,可以看出，传统的带隙基准电压源在－40～+125℃的温度范围中，最大和最小值之差仅为7.519mV，平均温度系数为37.07ppm/℃，该传统的带隙基准源在精度上已经无法满足大规模集成系统的要求。同时，该传统带隙基准结构在室温下温度系数为零，当温度大于或者小于室温时，负温度系数大于正温度系数，导致参考电压减小，造成精度减小。所以提出的改进型带隙基准源结构在温度大于或者小于室温时，分段对正温度系数进行补偿，以此提高带隙基准电路的精度。

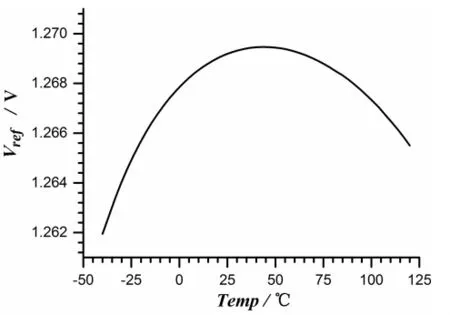
图2 传统Brokaw带隙基准结构的仿真结果

3 改进型带隙基准源结构

针对传统的Borkaw带隙基准电压源精度低，同时芯片集成规模越来越大，几个系统集成于一个芯片中，对带隙基准电压源的要求高。设计一种改进型的带隙基准源结构，通过这一结构，可在温度大于或者低于室温时，对正温度系数进行分段补偿，从而提高带隙基准源的精度。这一改进型带隙基准源的具体结构如图3所示。

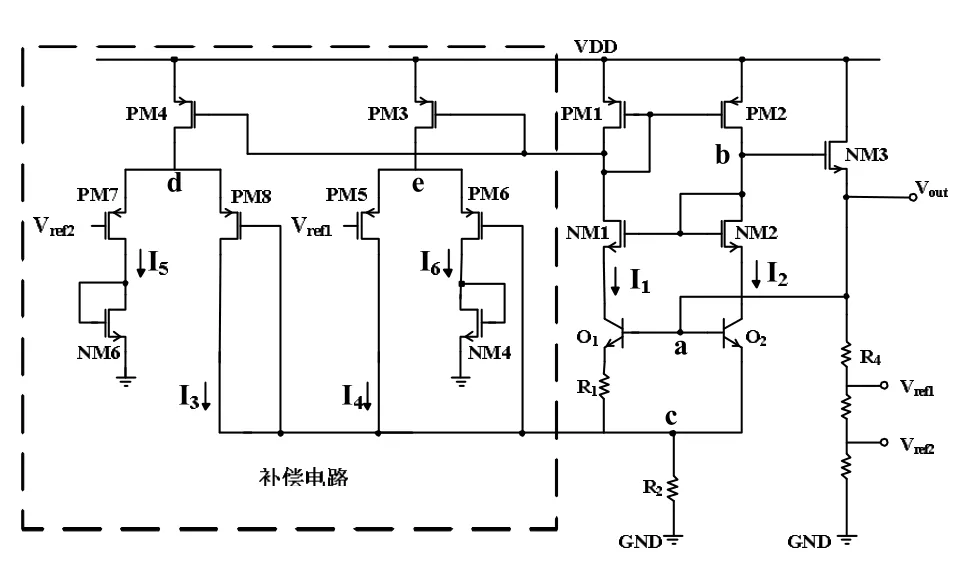
图3 改进型带隙基准源结构示意图

图中，由 PM1、PM2、NM1、NM2、Q1、Q2、R1、R2构成带隙基准核心电路，该核心电路的工作原理与上述传统带隙基准电路相同；虚线框内所示的电路为温度补偿电路，由PM3、PM4与PM1构成电流镜，流过PM3电流为X倍的I1电流，流过PM4的电流为Y倍的I1电流，（其中式中n表示Q1的有效发射面积是Q2的n倍）。当温度小于室温时，Vc电压降低，与Vref1和Vref2比较（其中电流I4趋近于0，I3电流增大，补偿正温度电压为所以在低补偿后的Vref为：

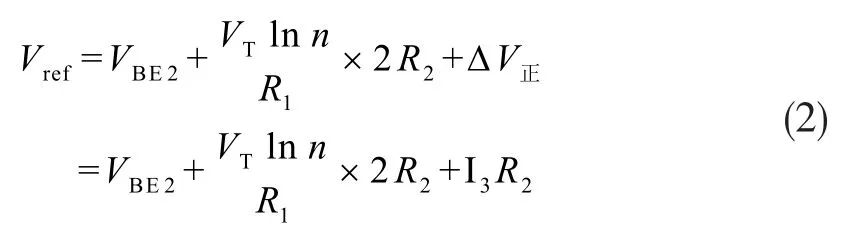
其中，当温度小于室温时，PM7和PM8工作在亚阈值区，得到下式：

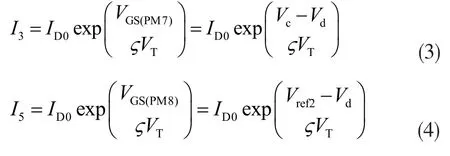
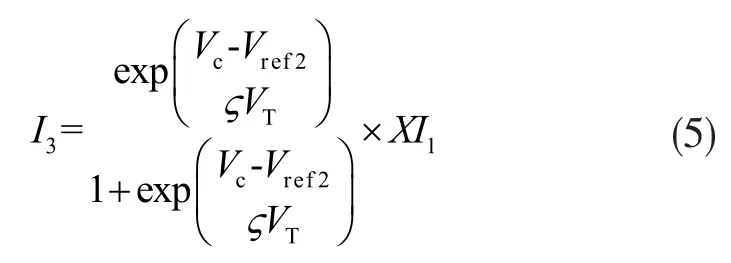
将式(5)带入式（2），可得在低于室温时，补偿后的基准电压：

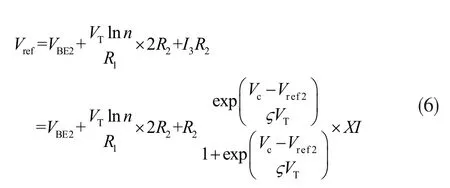
选择合适的Vref2值和X值，产生合适的正温度补偿电流I3，从而对基准电压源进行合适补偿。

当温度大于室温时，Vc电压升高，与Vref1和Vref2比较（其中电流 I3趋近于0，I4电流增大，补偿正温度电压为所以在高温补偿后的Vref为：

其中，当高温时的分段补偿正温度系数电流I4的推理与低温补偿电流I3的推理同理，选取合适的Vref1和Y值可以得到合适的补偿电流I4，从而对基准电压源进行合适补偿。

4 改进型带隙基准源仿真结果与分析

基于Nuvoton的0.35μm BCD工艺模型，使用Cadence的Specture工具对电路进行仿真分析。图4给出了在高温和低温下，补偿的正温度系数电流曲线。图5给出了在TT、FF、SS的工艺角下，补偿后的带隙基准电压温度特性曲线。仿真数据结果见表1。

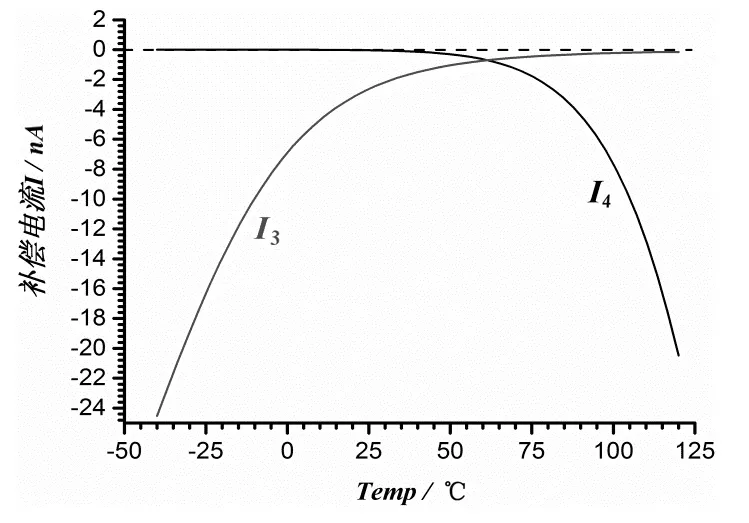
图4 高温、低温下补偿的正温度系数电流曲线

仿真结果表明，在不增加电路的复杂性的基础上，可实现一种具有高精度的带隙基准电路。经过在低温和高温分段正温度系数电流的补偿，在－40～+120℃的温度范围中，最大和最小值之差仅为871.9μV，平均温度系数为4.292ppm/℃。从表1的结果可见，在不同的工艺角下仿真，改进型带隙基准电路具有良好的稳定性。

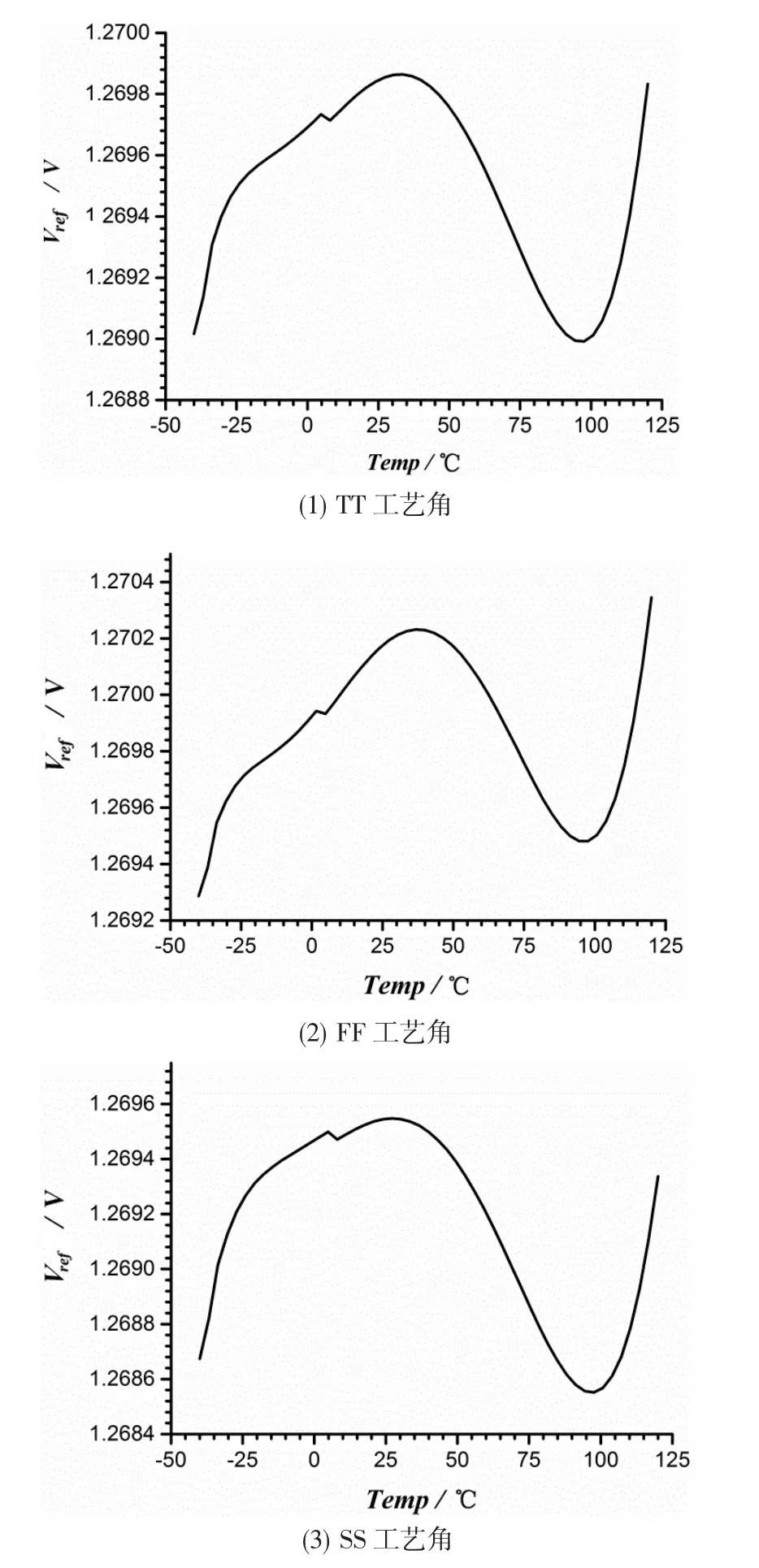
图5 输出基准电压在不同工艺角下的温度曲线

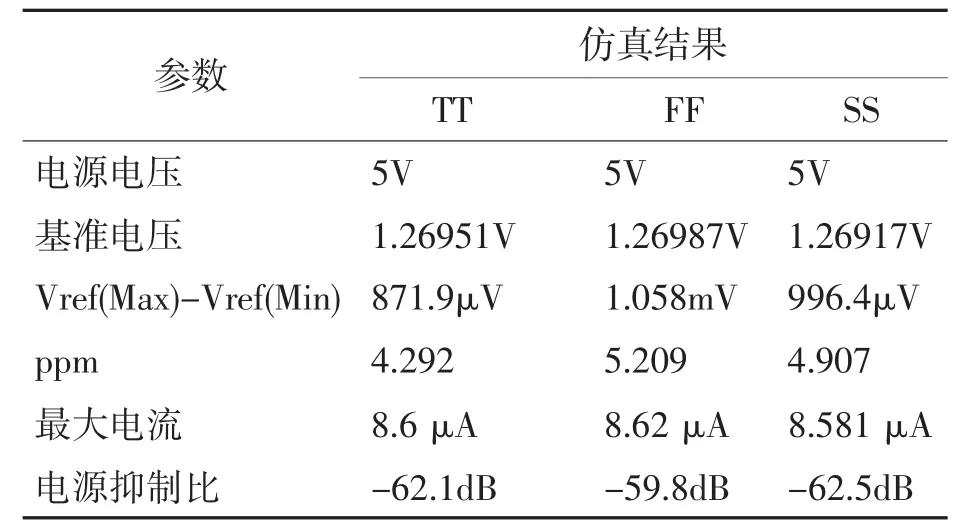
表1 带隙基准源在不同工艺角下的仿真结果

5 结束语

分析传统Brokaw带隙基准电路和改进型温度补偿带隙基准电路,在理论上阐述了传统带隙基准源在高温和低温下基准电压随温度变化大的不足，提出了一种具有正温度补偿的改进型带隙基准电路。通过一系列仿真结果显示，经过正温度系数补偿，带隙基准电压的温度系数明显减小，带隙基准源精度得到了提高。改进型带隙基准电路可以很好地满足集成电路系统对带隙基准源的低温度系数日益增长的需求。

参考文献：

[1]CHAHARDORI M,ATARODI M,SHARIFKHANI M.A sub 1V high PSRR CMOS bandgap voltage reference[J].Microelectronics Journal,2011,42(9):1057-1065.

[2]李睿，冯全源.一种高性能曲率补偿带隙基准源的设计[J].微电子学，2016,03:328-331.LI Rui,FENG Quanyuan.Design of a high performance curvature compensation bandgap reference[J].Microelectronics,2016,03:328-331.

[3]LIU Xi,LIU Qian,JIN Xiaoshi,et al.Negative voltage bandgap reference with multilevel curvature compensation technique[J].Journal of Semiconductors,2016,37(5):055008.

[4]SANBORN K,MA D,IVANOV V.A Sub-1V low noise bandgap voltage reference[J].IEEE Journal of Solid-State Circuits,2007,42(11):2466-2481.

[5]SU Kai,GONG Min,QIN Huaibin,et al.A multiple transistor combination low-voltage curvature-corrected bandgap reference[J].Journal of Semiconductors,2013,34(6):065010.

[6]ZHOU Q,YAN K,LIN J,et al.Novel high-PSRR highorder curvature-compensated bandgap voltage reference[J].Journal of China Universities of Posts&Telecommunications,2016,23(2):66-72.

[7]毕查德·拉扎维.模拟CMOS集成电路设计[M].陈贵灿,程军,张瑞智,等译.西安:西安交通大学出版社,2002.RAZAVI B.Design of Analog CMOS and Integrated Circuits[M].CHEN Guican,CHENG Jun,ZHANG Ruizhi,et al,transl.Xi'an：Xi'an jiaotong university press,2002.

[8]BROKAW A P.A simple three-terminal IC bandgap reference[J].IEEE Journal of Solid-State Circuits,1974,9(6):388-393.

[9]杨琦,张国俊.一种带有数字修调的高精度带隙基准电路[J].微电子学,2016,03:320-323.YANG Qi,ZHANG Guojun.A high precision bandgap reference circuit with Digital Trimming[J].Microelectronics,2016,03:320-323.