具有自主修正投放轨迹的装备空投的建模与仿真*

许 飞，许世蒙，杜建华，曹贻鹏

（1.陆军装甲兵学院基础部，北京 100072；2.陆军装甲兵学院科研部，北京 100072）

0 引言

装备自主精确空投［1］是指基本上完全依赖空降伞上配置的控制装置来实现精确定位目标的投放，其优势在于能够充分利用航天航空、气象、卫星、激光探测等现代科学技术手段，不断修正空投轨迹，以满足一定的投放要求。精确空投系统及技术的发展和应用是信息化条件下多兵种的联合作战，战时的快速反应、制胜的重要环节，是实现兵力、装备、补给等快速、精确送达的有效手段［2］，但在实战中，由于受到地域环境、气候条件、可见度以及地面和空中信号传输等不利条件的干扰，空投的精度还有待进一步提高，鉴于此本文从空投的建模和轨迹修正两个重要方面进行改进和优化来提高空投的精度。

目前装备空投过程多采用常微分方程建立模型，但该种方法建立的模型考虑的影响因素少，因素间关联度低，可扩展性差，不利于模型的完善和优化，在实战中会造成空投精度不高、落点分散、搜集困难、损耗偏高等问题，并且考虑到在一些极端天气或能见度低的情况下进行空投，空投的精度更加无法保证，为此本文将采用偏微分方程建立模型，使之更加贴合战场环境，同时在实际空投过程中，利用空降伞上的传感器监控、测算由投放点、投放速度、电磁干扰等不确定因素所引起的空投轨迹的偏移程度，单次、多次，甚至实时修正空投轨迹，从而不断地提高空投精度［3］。

通过对所建模型及轨迹修正理论进行仿真和多次模拟，并对仿真结果进行对比，采用偏微分方程建立模型并对空投轨迹进行修正能够缩小装备空投的着落点范围，提高空投的稳定性及精度。

1 装备空投动力学模型的建立

假定装备质量、重力及阻力分别为mw、Gw、Dw，降落伞的质量、重力及阻力分别为 ms、Gs、Ds，投放速度为，实时速度为，位移向量为。根据装备受力情况，以时间t和轨迹修正参数h为参量建立偏微分方程组模型：

2 变量动态分析

2.1 气压、温度对空气密度的影响

影响空气密度的因素主要有压强和温度，其关系为［4］

式中，kon=293 K为标准状态空气的温度；pon=101.325 kpa为标准状态空气的压强；ρon=1.29 kg/m3为标准状态空气的密度。

由式（7）～ 式（9）可知，在 2 000 m 处空气密度与地面处空气密度相差不大，为了便于运算，这里取平均值ρ=1.142 8 kg/m3代替。

2.2 装备所受空气阻力的分析

装备和降落伞在空气中所受风阻取决于物体的形状、迎风面积、空气密度、风阻系数以及相对运动速度，其关系式为［4-5］

式中，f为空气阻力；c为风阻系数；s为迎风面积；v为装备相对风的速度；n的取值与装备运动速度有关，通常认为 10 m/s时 n=1，10 m/s～311 m/s时 n=2。

2.3 降落伞面积的选取

降落伞面积的选取直接关系到装备减速效果和空投精度，进而影响投放轨迹的修正和装备搜寻，为此，降落伞的选取应保证在垂直方向上受力均衡［6-7］，则

式中，Dwz、Dsz分别为 Dw、Ds在垂直方向上的分量值；c1、c2分别为降落伞和装备的风阻系数，根据文献［5］取 c1=0.873，c2=1.28；s为降落伞面积；s2=22 m2为装备底部迎风面积，并假设装备质量为m=10 000 kg，通过式（10）可得降落伞面积为

在此面积下，装备可减速至安全落地速度以下，并保持该速度直至降落至目标点，联合式（1）～式（12）便得到装备运动微分方程组。

3 模型仿真及可靠性

利用MATLAB软件及采用蒙特卡罗法对添加随机因素后的空投轨迹进行一次、两次修正，以提高空投精度和规避障碍物，结果表明：对空投轨迹进行修正能够解决由投放误差所引起的精度降低的问题。

3.1 添加随机因素前后的MATLAB仿真

3.1.1 仿真中的参数设定

假定装备投放高度为h=2 000 m，装备连同降落伞的质量为m=10 000 kg，装备底部、前方、侧面面积分别为，装备投放时的速度为v=80 m/s，开伞时间为t=8 s，并忽略开伞对装备姿态的影响，在下降过程中装备受到水平风的影响，方向与装备滑行方向相反，且风力大小与装备所处高度有关，其关系为：

3.1.2 空投轨迹、速度及着落点范围

由3.1.1中的参数设定，采用离散化的方法对投放过程进行MATLAB仿真，可以得到装备空投过程中的实时高度和速度变化曲线。

图1 和图2是装备空投中速度、位移实时变化曲线。由图1可知，在垂直方向上，降落伞打开前后的速度发生很大改变，在较短时间内便降到5 m/s以下的安全速度，而在x轴方向，速度变化较缓，但在到达地面时，各方向的速度均已降至安全速度以下［8］。从图2中可以看到，在降落伞打开后，空投轨迹发生明显的变化，并且可知落地点的坐标是（3 551.8，0），显示出装备在水平方向发生了大的漂移，这必将会引起较大的投放误差，为装备的搜寻带来不便。

在实际的装备投放中，由于受到空投位置、速度及其他随机因素的影响，空投轨迹发生偏移，现假定空投位置的误差为10 m，空投速度的误差为10 m/s，风的方向水平不变，采用蒙特卡罗法模拟50次的空投过程［9］，其落点范围如图3所示。

由图3可知，当空投存在误差的情况下，装备着落点的范围为［-10，10］×［3 350,3 750］，与理论落点坐标（3 551.8，0）对比来看，在y轴存在约10 m的偏离，而在x轴则存在约200 m的偏离，需对空投轨迹进行修正。

3.2 空投轨迹修正及对比分析

3.2.1 空投轨迹修正

为提高空投精度，需要对空投轨迹进行修正，以实现装备准确、安全着陆［10-11］，根据投放环境，误差大小的不同，修正频率可以是一次、多次或实时修正，具体修正过程如图4所示。

图4 是装备空投轨迹修正的流程图，在本次仿真实验中，设定的修正频率为一次和两次，其中一次修正是在总高度的1/2处，两次修正分别在总高度的1/3和2/3处，轨迹修正后的落点范围如图5和图6所示。

由图5可知，经一次轨迹修正后的装备着落点范围在y轴存在9 m的偏离，在x轴则存在100 m的偏离，较上节未修正轨迹的投放范围有了明显的提升，约在x轴方向半径范围提高了50%，效果显著。图6是经两次轨迹修正得到的着落点范围，已知在x轴方向分布范围为［3 480，3 638］，较单次轨迹修正的着落点范围提高了21%，当然，若要继续提高空投精度，可对空投轨迹进行多次修正或实时修正。

3.2.2 轨迹修正的对比分析

上节从无随机因素影响、添加随机因素影响、对空投轨迹修正3个方面进行了仿真模拟，主要探索轨迹修正的参数设定、频率及强度，其仿真对比结果如表1所示。

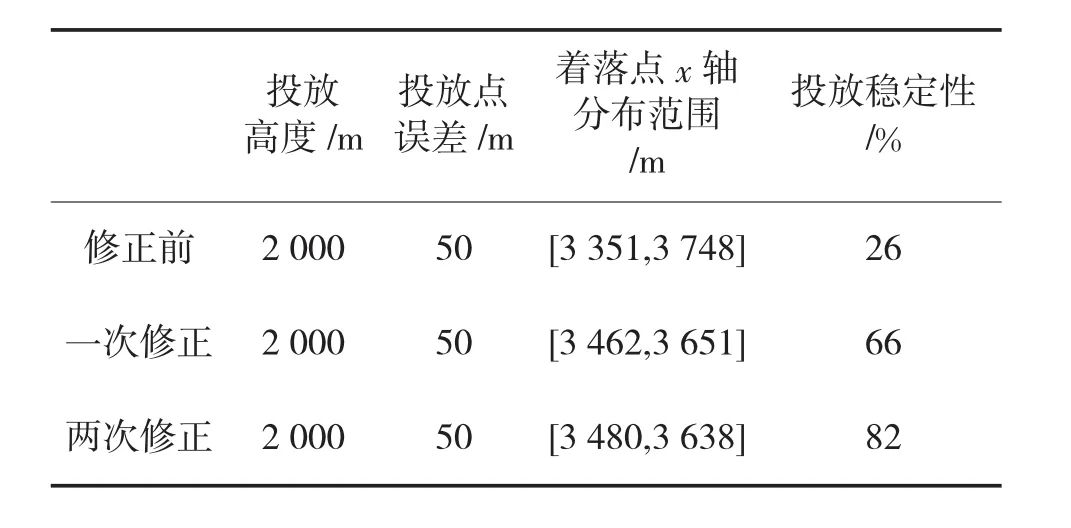
表1 轨迹修正后的仿真结果对比

从表1中可以看到，经单次轨迹修正后的装备着落点范围缩小了50%，两次轨迹修正后的着落点范围缩小了60.5%，投放精度和稳定性显著提升，本段关于轨迹修正的思想和方法是对后续更加精确的轨迹修正进行的有益探索。

3.3 障碍规避的空投轨迹修正

障碍规避［12-13］是指导航控制系统通过获取着陆区地形及障碍物信息，并结合装备位置、速度等状态参数，自主对空投轨迹进行修正，完成对障碍物的规避。本次仿真忽略障碍物形状，并设修正的目标距离为100 m以避开障碍物，其仿真结果如图7所示。

由图7可知，随着着落点的改变，也可通过控制器对空投轨迹进行修正以保证空投精度，但由于误差具有传递性，改变后的落点范围较不发生改变的落点范围有所增加，并且由于空投过程受不确定随机因素的影响，这也给控制器修正的力度、策略提出更高要求。

4 结论

本文对装备空投过程建立了偏微分方程组模型，并对该空投过程进行了仿真模拟，随后对仿真过程进行了单次和两次轨迹修正，从中可以看到空投精度在不断提高，同时又仿真模拟了为避开障碍物而采取的轨迹修正，这些仿真模拟的过程和结果表明，该偏微分方程组模型和轨迹修正理论能够提高空投的稳定性和精度，同时也有助于进一步研究空投轨迹的实时修正理论。

参考文献：

［1］王锐，孙昕，史晓春.精确空投系统的导航方法研究［J］.科学技术与工程，2011，11（28）：7028-7031.

［2］胡容，姚敏，赵敏，等.翼伞精确空投系统归航轨迹规划与控制［J］.指挥控制与仿真，2014，36（6）：111-116.

［3］叶培建，杨孟飞，彭兢，等.中国深空探测进入/再入返回技术的发展现状和展望［J］.中国科学·技术科学，2015，45（3）：229-238.

［4］许飞，许世蒙，杜建华，等.军用装备定点精确投放的建模与仿真［J］.装甲兵工程学院学报，2016，30（1）：99-103.

［5］李薇，黄振华，周群，等.无风条件下军用装备定点投放的数学建模与仿真［J］. 火力与指挥控制，2012，37（10）：43-45.

［6］TANG Q G，ZHANG Q B.Perturbation dynamics and its application for parachute munition system ［J］.Journal of China Ordnance，2007，3（4）：272-274.

［7］ZHU Y，LIU L，WANG Z P.Flow field characteristics for parachute-projectile system ［J］.Chinese Journal of Mechanical Engineering，2011，24（5）：813-819.

［8］WANG H Y，HONG H J.Environment adaptability evaluation for buffering airbag of heavy equipment during airdrop landing［J］.Journal of China Ordnance 2012，8（4）：223-229.

［9］GUO Z，MIAO Q L.Prediction of the trajectory of the manned spacecraft SHENZHOU-7 deploying a parachute based on a fine wind field ［J］.Science China Earth Science，2011，24（9）：1413-1429.

［10］郑成，吴庆宪，姜长生，等.基于IAGA的翼伞系统分段归航轨迹的优化［J］.电光与控制，2011，18（2）：69-72.

［11］王茜茜，谢慕君，李元春.基于模糊参数优化的小行星软着陆控制方法研究 ［J］. 深空探测学报，2015，2（2）：162-167.

［12］胡海静，朱圣英，崔远平.基于Lyapunov函数的小天体软着陆障碍规避控制方法［J］.深空探测学报，2015，2（2）：149-154.

［13］唐波，高军，李良春，等.精确空投系统投放点确定的辅助决策模型构建［J］.装备指挥技术学院学报，2010，21（2）：123-125.