基于局部动态贝叶斯网络的无人机态势评估*

袁覃恩，慕晓冬，易昭湘，王诺娅

（1.火箭军工程大学，西安 710025；2.武汉科技大学管理学院，武汉 430065）

0 引言

无人机（Unmanned Aerial Vehicle）［1］拥有成本低廉，机动性好，使用方便，操作简单等优点，在诸如侦查、航摄、监控、物品投送等方面具有很大的应用空间。近年来，无人机技术发展十分迅速，无人机控制系统的发展也有着智能化、自主化的趋势。无人机本身动力较小，受天气、地形等环境因素影响较大，自主飞行中无人机控制系统缺乏对飞行过程中突发事件的应急处理能力。因此，深入研究无人机态势实时评估方法能够提高无人机执行任务的可靠性，避免事故，降低损失。

近年来，众多学者对态势评估技术进行了深入的研究，取得了一系列成果。文献［2］运用串联电阻分压法、改进AHP法和熵权法3种方法对空战威胁指标权重进行计算，为评估空战威胁提供了一种可行方法。文献［3］提出了一种采用分层贝叶斯网络的自适应态势评估，提高了评估系统鲁棒性。文献［4］运用变权综合评估模型实现了对即时航迹优劣的评估，具有良好的时效性。文献［5］提出了一种结合动态贝叶斯网络和方差变换的方法来感知车辆自动变道中的不确定因素，并运用于实际。文献［6］运用变结构动态贝叶斯网络将分类信息的不确定度作为态势评估的证据，使用概率推理实现动态环境下的态势评估，能够处理无人机飞行过程中的不确定性信息。在态势评估众多方法中动态贝叶斯网络能够处理不确定性信息且能够进行实时评估，具有较高的可用性和较大的潜力，是当前研究的热点。但是运用动态贝叶斯网络算法对无人机进行实时态势评估过程中注重信息的传递和积累，忽略了突发状况结束后不会对无人机飞行产生持续影响的实际情况。

局部动态贝叶斯网络方法是在对航迹分段的基础上对态势进行实时评估，能够对突发状况进行感知，为控制系统实时决策提供支持。该方法基于任务实际情况简化了网络拓扑结构，对突发状况具有较强的敏感性，在突发状况结束后能屏蔽突发状况对态势的持续影响，更加贴合评估需求。

1 动态贝叶斯网络（DBN）

贝叶斯网络［7］（BN）是一种图形化的建模工具，它将图论和概率论相结合对不确定事件进行分析和推理，不仅具有完备的数学基础，同时也具备直观的知识表示，已经在众多领域中得到广泛的应用。BN推理与一般的知识表示方法不同的地方在于当证据发生改变时，BN不需要重新建立模型。变量在更多的情况下会随着时间的改变而改变，而静态BN无法处理对时间敏感的事件，因此，学者们提出了动态贝叶斯网络［8］（DBN）用于解决时序问题。

2 局部动态贝叶斯网络（Local Dynamic Bayesian Network，LDBN）

2.1 基本思想

2.1.1 路径分段

根据历史观测数据中地形、气象等情况进行分区，将地形、气象条件相近且相邻的区域划分为同一区域。根据划分的区域，将UAV飞行过程中位于同一区域的路径划分为同一路径段，完成对UAV飞行路径的分段。

2.1.2 局部子网络

在飞行过程中某一段的飞行必须依赖于前置路径段的完成，如果前置的飞行没有完成，则该路径的飞行无法进行。基于这种强烈的依赖关系，每次进行推理前对路径段进行判定，经过判定后各个路径段的飞行过程相互之间可以视为独立。为同一路径段的飞行建立局部子网络，不同路径段的子网络相互独立，当前执行过程只需要构建当前路径的局部动态贝叶斯网络，得到当前路径段完成的概率。

2.1.3 子网络之间信息传递

已经完成的飞行结果是确定的，每次推理前进行判定，进入下一路径段时只需要将前置任务完成状况作为证据输入下一路径段的局部贝叶斯子网络中，其他无用信息舍去。已经完成的路径段从估计模型中删去，减少网络的复杂度。

2.2 贝叶斯网络证据

UAV飞行过程中可能受到的影响因素主要有风、雨、雪等天气因素，地形，电磁环境等环境因素，以及其他飞行物等偶然状况。因此，贝叶斯网络证据分为3类：

第1类，地形等固定证据，随着各个区域的划分，这一类证据根据各区域的具体情况而定，对各区域而言是始终存在且固定不变的，其条件好会提高飞行态势的值，其条件较差则会降低飞行态势的值。

第2类，天气等条件证据，这一类证据始终会存在且会随时间发生变化，其条件好会提高飞行态势的值，其条件较差则会降低飞行态势的值。

第3类，区域内的突发情况，这一类证据并不一定会存在，因此，在计算中只考虑这一类证据的出现会降低飞行态势的值，未出现突发情况则并不增加飞行态势的值。

2.3 推理算法

目前DBN的精确推理算法［9］主要包括前向后向算法（Forwards-Backwards，FB）算法，边界算法（Frontier Algorithm）以及接口算法（Interface Algorithm）等。由于边界算法及接口算法运用了图形变换，在处理较大规模贝叶斯网络时具有优势，但算法复杂度较高，对无人机机载计算机负担过重，而当前问题网络规模较小，为保证算法实时性，采用FB 推理算法［10］：

2.3.1 前向算子

2.3.2 后向算子

2.3.3 后验概率

同一时间片的前向、后向计算结果相乘得到在当前观测证据条件下的事件状态的后验概率。

2.4 算法流程

评估算法流程如图2所示。

评估算法基本步骤如下：

Step1：读取UAV飞行航迹。

Step2：对航迹进行分段，并将所有航迹段完成标志置0。

Step3：检查到的第一个标志非1的航迹段作为当前段，若所有完成标志均为1，则跳转至Step8。

Step4：读取当前段的先验概率并将时间参数T置为1。

Step5：读取当前时刻T的观测数据。

Step6：在观测数据和先验概率基础上，运用前向后向算法建立当前飞行段的局部动态贝叶斯子网络，对UAV飞行态势进行估计并输出。

Step7：对比当前UAV所处位置和航迹分段信息判断该飞行段是否结束，若已结束，将航迹完成标志置1，进入下一路径段，跳转至Step8；若未结束，则时间参数T增加1，进入下一时间片，跳转至Step3。

Step8：飞行结束。

3 仿真实验

假设UAV执行物品投送任务，根据UAV的飞行路径，UAV从A1区域的S点起飞，依次飞过区域A2、A3、A4、A3，到达终点 A5 区域的 D 点。根据飞行区域的历史观测数据，将飞行路径划分为5个阶段。图3给出无人机初始飞行航迹示意图。运用Matlab平台进行仿真实验，对观测数据进行分级预处理得到推理证据，每次推理输入评估系统的数据为一个1×6数组

式中，A（area）为划分区域后当前所在区域的编号；T（terrain）为当前区域地形数据；W（wind）为当前风力情况数据；R（rain）为当前下雨情况数据；I（interference）为当前受到干扰情况；E（emer-gency）为是否监测到突发状况。输出结果为当前状态下态势评估结果。

3.1 实验1

Step1：给定一组观测数据（无突发状况）运用动态贝叶斯网络（DBN）对态势进行估计，画出态势曲线；给定的观测数据中固定证据及条件证据保持不变，在第8时刻添加遇到其他飞行器的突发状况，运用动态贝叶斯网络（DBN）对态势进行估计，画出态势曲线。

Step2：给定一组观测数据（无突发状况）运用局部动态贝叶斯网络（LDBN）对态势进行估计，画出态势曲线；给定的观测数据中固定证据及条件证据保持不变，在第8时刻添加遇到其他飞行器的突发状况，运用局部动态贝叶斯网络（LDBN）对态势进行估计，画出态势曲线。

实验1结论：

图4为动态贝叶斯网络算法对飞行任务态势的估计，图5为局部动态贝叶斯网络算法对飞行任务态势的估计。由两图对比可知，两种方法均能够对条件的变化以及突发状况有较好的感知，但在突发状况结束后局部动态贝叶斯网络估计算法能屏蔽突发状况对态势的持续影响，更加贴合其他飞行器，一旦飞过就不再对UAV产生影响的实际情况。

3.2 实验2

Step1：在给定的一组观测数据中固定证据及条件证据均相同情况下，分别运用动态贝叶斯网络（DBN）和局部动态贝叶斯网络（LDBN）对态势进行估计，画出态势曲线。

Step2：给定的一组观测数据中固定证据及条件证据与Step1中保持不变，在第8时刻添加遇到其他飞行器的突发状况，分别运用动态贝叶斯网络（DBN）和局部动态贝叶斯网络（LDBN）对态势进行估计，画出态势曲线。

实验2结论：

下页图6中未发生突发事件，该图反映的是动态贝叶斯网络算法与局部动态贝叶斯网络算法在态势估计中对变化的条件证据感知敏感度的对比，由图中曲线走势可知，LDBN算法的态势曲线在第20、21时刻出现了明显波动，但DBN算法对这一波动却无法感知。LDBN算法由于摒弃了已完成区域的无效数据，在UAV态势估计中对条件证据的感知比DBN算法更为敏感。

图7中两条曲线是固定证据及条件证据相同，第8时刻遇到其他飞行器情况下的态势估计曲线。该图反映的是动态贝叶斯网络算法与局部动态贝叶斯网络算法在态势估计中发生突发状况下局部情况的对比。由图7对比结果可知，第8时刻发生突发状况后，LDBN算法的态势曲线下降幅度明显大于DBN算法，在对突发事件的感知上LDBN算法比DBN算法更为敏感。

3.3 实验3

将实验2重复进行10次，记录所有单次推理的运算时间，分别计算相同条件下两种方法运算时间的平均值和最大值。

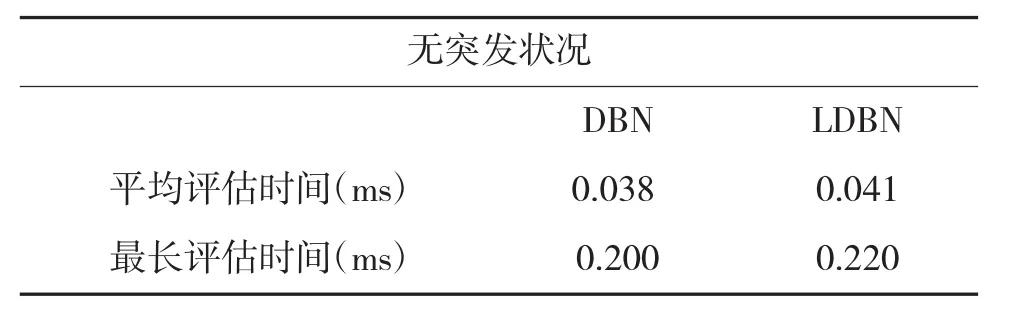
表1 无突发情况330次评估时间

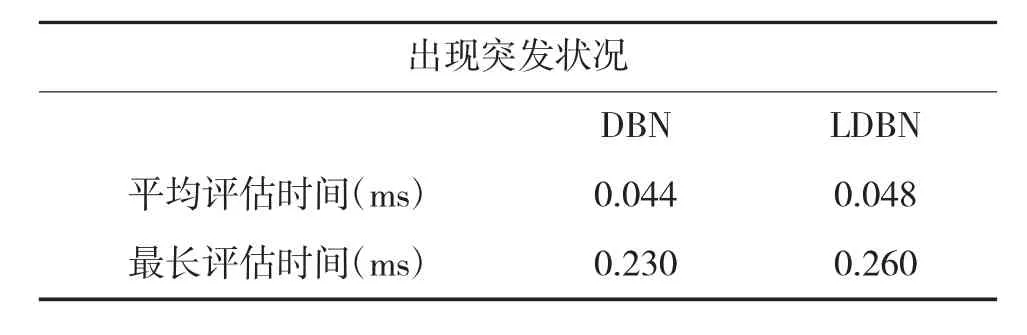
表2 出现突发情况330次评估时间

实验3结论：

由表1、表2中数据可知，在无突发情况下LDBN算法平均运算速度较DBN算法下降7.89%，最长评估时间长0.02 ms；在出现突发情况下LDBN算法运算速度较DBN算法下降9.09%，最长评估时间长0.03 ms。综上，LDBN算法较DBN算法运算速度有所下降，仍具有与动态贝叶斯网络接近的实时性，符合实时评估要求。

4 结论

本文在贝叶斯网络算法的基础上，考虑UAV飞行过程中的实际情况，对飞行路径进行分段处理，在路径分段基础上对动态贝叶斯网络估计算法进行改进，提出了局部动态贝叶斯网络算法并进行了实验验证，结果表明该方法有效可行，在突发状况结束后，局部动态贝叶斯网络估计算法能屏蔽历史突发状况对态势估计的错误影响，提高了局部态势估计中对条件证据和突发状况感知的敏感性，对无人机态势实时评估具有参考意义。

参考文献：

［1］WATTS A C，PERRY J H，SMITH S E，et al.Small unmanned aircraft systems for low-altitude aerial surveys［J］.Journal of Wildlife Management，2016，74（7）：1614-1619.

［2］程天发，葛泉波，陈哨东，等.基于改进空战威胁评估模型的权重计算方法比较［J］.火力与指挥控制，2016，41（1）：32-36.

［3］LI C，CAO M，TIAN L.Situation assessment approach based on a hierarchic multi-timescale bayesian network［C］//International Conference on Information Science and Control Engineering.IEEE，2015：911-915.

［4］曹岱伟，刘刚.低空飞行器即时航迹评估方法及模型［J］.现代电子技术，2014，38（2）：6-8.

［5］ULBRICH S，MAURER M.Situation assessment in tactical lane change behavior planning for automated vehicles［C］//IEEE，International Conference on Intelligent Transportation Systems.IEEE，2015：975-981.

［6］王长清，王振玲.基于时变贝叶斯网络的无人机态势评估模型［J］.计算机工程，2011，37（15）：152-154.

［7］PEARL B J.Probabilistic reasoning in intelligent systems：network of plausible inference［C］//Designing Intelligent Systems：UNIPUB，1984：1022-1027.

［8］DEAN T，KANAZAWA K.A model for reasoning about persistence and causation ［J］.Computational Intelligence，1989，5（2）：142-150.

［9］ANDRIEU C，DAVY M，DOUCET A.Efficient particle filtering for jump markov systems.application to time-varying autoregressions［J］.IEEE Transactions on Signal Processing，2003，51（7）：1762-1770.

［10］高晓光，陈海洋，符小卫，等.离散动态贝叶斯网络推理及其应用［M］.北京：国防工业出版社，2016：47-50.