含风电场概率最优潮流的拟蒙特卡洛算法
李泳泉
(国网浙江云和县供电有限公司,浙江 云和 323600)
风力在清洁能源中占有不可替代的位置,云和县内风力资源丰富,境内黄源风电站现已建成并接入电网。在风电场接入电网后, 积极收集相关运行数据,开展相关分析研究工作。相邻风电场在并网运行后,其出力之间往往存在一定的相关性;风电场并入电网运行后,出力的随机性和相关性对电力系统影响不可忽略。在电网规划与运行中,概率最优潮流(Probabilistic Optimal Power Flow,简称P-OPF)能评估电力系统中各种不确定因素,有助于潜在薄弱环节的提前发现和解决,降低电网运行风险。
P-OPF将电力系统中的不确定量视为服从某种概率分布的随机变量,通过输入变量的统计信息来求取输出变量的统计信息,比如各阶统计矩、概率密度函数(Probability Density Function,简称 PDF)、累积分布函数(Cumulative Distribution Function,简称CDF)等。现存的P-OPF问题解法主要有蒙特卡洛模拟法[1](Monte Carlo Simulation,简称MCS)、累积量法[2-5](Cumulant Method)和点估计法[6-7](Point Estimate Method)。
这三种方法中,MCS的适用性最广,只要建立相关的非正态随机变量的数学模型,再生成大量样本进行最优潮流(Optimal Power Flow,简称OPF)计算,进而输出变量的统计矩、PDF和CDF能够准确得到。但MCS最后结果的准确、收敛需要庞大的计算量来支撑。
累积量法将P-OPF计算中的优化过程视为一种概率映射,通过线性化潮流运算模型来求取输出量的统计信息。但该方法有两个不足,由于P-OPF计算中不等式约束的存在,输出量与输入量间函数关系的非线性很大,线性化该函数关系引入的误差不可忽略;累积量法在相关性的处理上需繁杂的数学计算保证,并且输入变量之间必须相互独立,而风电场机组出力之间的相关性必须考虑。
点估计[8]则是采用另一种方法来逼近输出、输入量间的函数关系。 在概率潮流问题中,能较准确地求得输出量的数学期望和标准差[9-10],易于输入变量相关性的处理[11-12]。 但其为减小计算量而引入的误差也是很大的,不能准确求取输出量的高阶统计矩[13-14]。 在 P- OPF运算中,由于不等式约束的限制,即使输入随机变量是正态的,输出变量也不是正态的, 不少输出变量的概率分布甚至是截断的,该方法的精度更是不够。
这三种方法均存在不足之处,将采取拟蒙特卡洛法(Quasi Monte Carlo Simulation,简称QMCS)来求取输出量的统计矩。为达到加快收敛速度和保证较高的精度目的。将采用Sobol数列中的低偏差序列(Low Discrepancy Sequence)替代MCS的伪随机序列(Pseudo Random Sequence)的方法。考虑到随机因素的相关性对概率最优潮流的显著影响[1],本文用 Nataf转换对输入变量间的相关性进行处理,用基于 Gauss- Hermite积分的插值法求解原相关的随机变量映射到标准正态空间的相关系数,通过 Cholesky分解将问题转换到独立的正态空间。同时,利用输出变量的概率加权矩(Probability Weighted Moments,简称PWM),通过多项式转换模型来建立输出量的PDF和CDF。
1 Nataf转换
相邻区域的风电场风速因素可视为相关的非正态随机向量。考虑到直接得到多变量联合概率分布函数较为困难。联合概率分布模型是常用的方法之一,该模型能满足各个变量之间的相关性。在概率分布问题处理中,正态分布拥有难以比拟的易处理特点,通过多维正态分布的联合概率密度函数建立多维非正态随机变量的模型, 即 Nataf变换[15-16],在工程应用中较多使用。 这里介绍一种用Nataf变换来生成风电场风速样本的方法。
设有随机变量,其CDF为F(x);z为服从标准正态分布的随机变量,其CDF为Φ(z)。根据等边际概率原则有:
F(x)=Φ(z)
(1)
则可表示为
x=F-1[Φ(z)]
(2)
将两个相关的随机变量x1、x2分别由z1、z2表示,为确保经由式(2)转换得到的随机变量x1、x2间的相关系数为ρx,需确定z1、z2间的相关系数ρz。ρx、ρz有如下函数关系:

(3)
式中φ(z1,z2,ρz)——二维标准正态分布的联合概率密度函数;μi、σi——xi的数学期望和标准差(i=1,2)。
对于给定的ρx值,直接通过求解式(3)中的积分方程来求得ρz是很困难的。但注意到ρx是关于ρz的连续函数,且相关系数ρz的取值位于区间[1,-1]内,因此可以用一个关于ρz的多项式来逼近两者的函数关系。
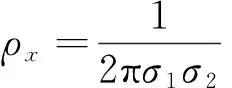
(4)
(5)
通过对各类概率分布的测试,一个阶数不超过9阶的多项式便可非常精准地逼近ρx、ρz的函数关系(n≤9)。式(4)中的二重积分可由11点的Gauss-Hermite积分准确求得。
对于给定的ρx值,求解式(5)中的一元n次方程便可求得ρz,所求的ρz应满足如下条件:
|ρz|≤1,ρzρx≥0
(6)
设随机向量X=(x1,…,xi,…xm)T的相关系数矩阵为Rx,可将式(2)由标准正态随机向量Z=(z1,…,zi,…zm)T表示。对X中的任意两个元素xi、xj(i≠j),zi、zj间的相关系数可由插值法求得,从而得到Z的相关系数矩阵Rz。对Rz进行Cholesky分解。便可将Z由相互独立的标准正态随机向量U表示:
Z=LU↔U=L-1Z
(7)
RZ=LLT
(8)
L为下三角矩阵。
通过式(7)、式(2),可以将独立的标准正态随机向量U转换成具有指定边际概率分布和相关系数矩阵Rx的非正态随机向量X,利用多维正态分布的联合概率密度函数描述相关的非正态多维随机变量。
2 拟蒙特卡洛
P-OPF的实质可定性为一个随机非线性规划问题:
min{f(x)|g(x)=b0,h(x)≤0|}
(9)
其中:g(x)=b0表示P-OPF计算中的等式约束,h(x)≤0表示不等式约束,P-OPF的数学模型可参见文献[1]和[6]。
假定电力系统中各随机因素组成的向量表示成X=(x1,…,xi,…xm)T。不考虑P-OPF的具体运算过程,输出变量y和X之间的关系表达为
y=H(x1,…,xi,…Xm)
(10)
经由Nataf转换,可将xi由ui表示,将y视为ui的函数:
y=H*(u1,…,ui,…Um)
(11)
经过式(1)的边际转换后,可以得到一个标准均匀分布空间:
ui=Φ-1(si)
(12)
si为标准均匀分布随机变量(si∈[0,1])。此时,y可表示为
y=h(S)S=(s1,…,si,…sm)
(13)
QMCS的基本思路通过计算输出变量的数学期望为例来展示:
(14)
式(14)的积分区域是m维单位空间[0,1]m。
在空间[0,1]m内随机选取点列Sj,应用MCS,对式(14)求积分,得到yj的数学期望:
(15)
通过算法生成伪随机序点列Sj,为确保所得的E[y]值准确收敛,点列数n通常很大,计算时间长。本文采取QMCS来改善计算的收敛速度和精度,即:选取尽可能均匀地分布在m维空间[0,1]m的点列Sj,以低偏差序列来替代MCS的伪随机序列,从而以较小的计算量得到较高精度的结果。
Sobol数列[18]在高维空间内的均匀性较好,本文选用Sobol数列进行计算。计算过程中所选点列是确定的,采用一种选取n个点列的点估计方法,为兼顾计算量和所得结果的精度,选用前(2-2001)列的Sobol数列进行运算。
3 多项式转换模型
对于概率分布未知且只有观测样本的随机变量,需要找到一个合适的模型来表述其分布情况。本文采用基于韦伯分布(α=1,β=4)的多项式转换模型对样本进行分布拟合。
设随机变量t服从韦伯分布W(1,4),由式(1)边际转换可得:
x=F-1[W(T)]
(16)
用一个10阶多项式逼近函数F-1[W(T)]:

(17)
解出系数ak,随机变量x可用韦伯分布对其进行表达。
随机变量的各阶统计矩可以描述其统计特性,只要使得式(17)中多项式模型的统计矩等于x的统计矩,便可得到较佳的模拟效果。本文采用PWM来确定ak的值。
随机变量的r阶PWM(βr)定义[19]如下:
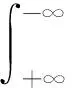
(18)
式(17)多项式模型的βr为
(19)
W(t)、w(t)分别为韦伯分布W(1,4)的CDF和PDF。Mk,r定义如下:

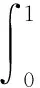
(20)
M0,0-M10,10可通过数值积分得到。
对于离散系统,可以将变量因素按x1≤…xi≤…≤xn排序,则βr的无偏估计值[20]如下:
(21)
依式(21)求解得到的前11阶PWM,利用式(19),得到如下的线性方程组:
(22)
求解方程得到系数ak。
需要说明的是,韦伯分布的逆累积分布函数(Inverse Cumulative Distribution Function,简称ICDF)存在闭式解析式:
t=[-ln(1-s)]1/4
(23)
式中s——标准均匀分布随机变量。
将式(23)代入式(17)就可以得到ICDF:

(24)
使用ICDF的优点在于:对于给定的概率点,可通过式(24)直接求得x的分位数。
4 算法步骤
本文求解P-OPF问题的具体步骤如下。
(1)选取m维Sobol数列的前(2-2001)点列,m为输入变量的个数。通过式(12),解得转换到标准正态空间后的向量Uj。
(2)根据各输入变量的ICDF,对式(3)用插值法求得任意两个变量xi、xj在标准正态空间的相关系数ρz,建立相关系数矩阵Rz。
(3)按式(8)把Rz实行Cholesky分解,得到矩阵L(下三角),向量Uj转换为向量Zj,zj=LUj。
(4)将向量Zj中的各元素zj,i依其ICDF按式(2)转换为xj,i,得到向量Xj。
(5)通过Xj代入到OPF,得到样本的输出量。
(6)利用所得的2 000个样本求得各输出变量的数学期望和标准差;根据式(21)求出其前11阶PWM,代入式(22)解得ak,得到式(24)的ICDF,最后得到PDF、CDF。
MCS法的样本也可先生成维相互独立的标准正态随机向量,再依步骤2-4生成样本即可。
5 算例分析
利用文献[1]中算例,其中均值为静态平衡点处的有功负荷值,而有功负荷服从一般正态分布,均值的5%取为标准差,风力发电的出力之间还应考虑更强的相关性:

以105次MCS计算结果作为比较基准,2 000次QMCS、MCS得到的数学期望、标准差的相对误差平均值如表1所示。

表1 QMCS与MCS的误差比较
由表1数据可知,次数相等情况下,QMCS所得数学期望和标准差的精度值要明显高于MCS;由于 QMCS使用确定点列计算,其收敛性要优于MCS。以有功潮流数学期望相对误差平均值这个指标为例,执行10次MCS(2000次)运算,其误差波动范围为0.383~2.053。
对各输出变量,基于所得的样本,依式(24)求出其ICDF,在5%、25%、50%、75%、95%处求得对应的分位数,最后计算其和MCS(105次)所得结果的相对误差平均值,如表2所示。
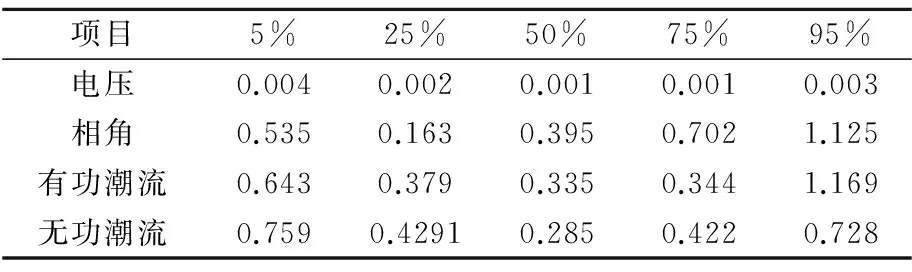
表2 基于多项式模型所得分位数的误差
输出变量的概率分布通过多项式模型可以精确描述。
以线路32-113的无功潮流为例,其对应的多项式模型系数如表3所示;所得 PDF、CDF如图1、图2所示,单峰概率分布很难描述线路32-113的无功潮流,本文提出的模型能够很精确地求解出相对应的 PDF、CDF图。
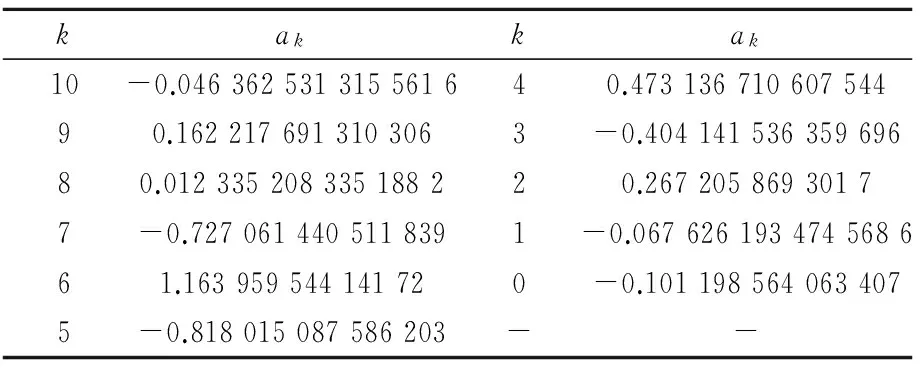
表3 多项式模型的系数(线路32-113无功潮流)
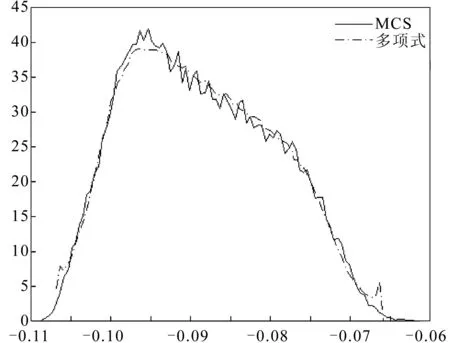
图1 线路32-113无功潮流的概率密度函数
在图1的右端,可以看到有一个误差呈现明显尖峰状。对P-OPF所有的输出变量进行模拟测试,此误差位于部分不规则概率分布的PDF两端,但由多项式模型建立的CDF位于5%~95%这一概率区间段的模拟效果,依旧很准确。

图2 线路32-113无功潮流的累积分布函数
6 结语
针对MCS法、累积量法、点估计法等P-OPF计算方法的不足,本文基于QMCS提出了一种求取P-OPF输出变量PDF、CDF的方法。 该方法具有如下特点:只需一次插值就能得到任意两种概率分布的相关系数计算公式,且能对服从任意连续概率分布随机变量间的相关性进行处理;较小计算量即可准确求得输出变量的数学期望、标准差等统计信息;对服从不规则分布输出量的PDF、CDF进行描述;在相同的计算次数下,其收敛性和精度要优于MCS。
参考文献:
[1] 杨欢,邹斌.含相关性随机变量的概率最优潮流问题的蒙特卡罗模拟方法[J].电力系统保护与控制,2012,40(19):110-115.
YANG Huan,ZOU Bin.A Monte Carlo simulation method for probabilistic optimal power flow with correlated stochastic variables[J].Power System Protection and Control,2012,40(19):110-115.
[2]M M,P K,Q V H.Probabilistic optimal power flow[C]//IEEE Canadian Conference on Electrical and Computer Engineering,Waterloo,Canada,1998.
[3]S A,R W,A J.Cumulant- based probabilistic optimal power flow(P-OPF) with Gaussian and Gamma distributions[J].IEEE Transactions on Power Systems,2005,20(2):773-781.
[4]S A,R W,A J.Cumulant based probabilistic optimal power flow (P-OPF) [C]//International Conference on Probabilistic Methods Applied to Power Systems,Ames,American,2004.
[5]S A,R W,A J.Introduction to cumulant-based probabilistic optimal power flow (P-OPF)[J].IEEE Transactions on Power Systems,2005,20(2):1184-1186.
[6]V G,C C A.Probabilistic Optimal Power Flow in Electricity Markets Based on a Two-point Estimate Method[J].IEEE Transactions on Power Systems,2006,21(4):1883-1893.
[7]潘炜,刘文颖,杨以涵.概率最优潮流的点估计算法[J].中国电机工程学报,2008,28(16):28-33.
PAN Wei,LIU Wenying,YANG Yihan.Point Estimate Method for Probabilistically Optimal Power Flow Computation[J].Proceedings of the CSEE,2008,28(16):28-33.
[8]H H P.An efficient point estimate method for probabilistic analysis[J].Reliability Engineering and System Safety,1998,59(3):261-267.
[9]S C L.Probabilistic Load-Flow Computation Using Point Estimate Method[J].IEEE Transactions on Power Systems,2005,20(4):1843-1851.
[10]M J M,P R J.Point Estimate Schemes to Solve the Probabilistic Power Flow[J].IEEE Transactions on Power Systems,2007,22(4):1594-1601.
[11]M J M,B L,C A J,et al.Probabilistic power flow with correlated wind sources[J].IET Generation Transmission and Distribution,2010,4(5):641-651.
[12]杨欢,邹斌.含相关性随机变量的概率潮流三点估计法[J].电力系统自动化,2012,36(15):51-56.
YANG Huan,ZOU Bin.A Three-point Estimate Method for Solving Probabilistic Power Flow Problems with Correlated Random Variables[J].Automation of Electric Power Systems,2012,36(15):51-56.
[13]U J.Probabilistic load flow with correlated wind power injections[J].Electric Power systems research,2010,80(5):528-536.
[14]U J.Probabilistic load flow in systems with wind generation[J].IET Generation Transmission and Distribution,2009,3(12):1031-1041.
[15]L P L,D K A.Multivariate distribution models with prescribed marginals and convariances [J].Probabilistic Engineering Mechanics,1986,1(2):105-112.
[16]Q X.Evaluating correlation coefficient for Nataf transformation [J].Probabilistic Engineering Mechanics,2014(37):1-6.
[17]N J C,S A F M.Applications of a method for the efficient computation of posterior distributions [J].Journal of the Royal Statistical Society. Series C (Applied Statistics),1982,31(3):214-225.
[18]M W J,C R E.Quasi-Monte Carlo integration[J].Journal of Computational Physics,1995, 122(2):218-230.
[19]G J A,L J M,M N C.Probability weighted moments: definition and relation to parameters of several distributions expressable in inverse form[J].Water Resources Research,1979, 15(5):1049-1054.
[20]H J R M,W J R,W E F.Estimation of the generalized extreme-value distribution by the method of probability-weighted moments [J].Technometrics,1985, 27(3):251-261.

