页岩气渗流机制数学表征及Knudsen扩散影响分析

刘 骞

(中国石油集团长城钻探工程有限公司， 辽宁 盘锦 124010)

随着全球能源结构发生改变，页岩气在全球能源体系中发挥的作用越来越大[1]。页岩气藏的孔隙直径为纳米级，属于超低孔、超低渗的致密多孔介质，且赋存方式多样[2-5]。通常，页岩气在页岩气藏内的流动特征受“微尺度流动”下多重渗流机制的共同影响[6]，其中以黏性流、Knudsen扩散和吸附 — 解吸附作用等渗流机制为主。本次研究中，将考虑基质和裂缝的黏性流及Knudsen扩散作用，采用Langmuir等温吸附方程表征气体分子在基质孔隙的吸附与解吸附作用。同时，通过Knudsen扩散的质量流量公式，分析孔隙半径、压力和温度变化对质量流量的影响。

1 页岩气渗流机制及其数学表征

1.1 黏性流

当气体分子平均自由程小于孔隙直径时，分子与壁面的碰撞较少，主要以分子间的碰撞为主。此时，由压力梯度引起的气体流动称为黏性流，其质量流量可以用达西定律来表示[7]：

(1)

式中：Nv—— 黏性流引起的质量流量，kg(m2·s)；

kmi—— 基岩渗透率，m2；

pm—— 基岩孔隙压力，Pa；

ρm—— 基岩气体的密度，kgm3；

μg—— 气体黏度，Pa·s。

1.2 Knudsen扩散

当气体在多孔固体中扩散时，如果孔径小于气体分子的平均自由程(约0.1 m)，则气体分子对孔壁的碰撞，较之气体分子间的碰撞要频繁得多。此时气体之间的质量流量可以用Knudsen扩散公式[8]表示：

Nk=-MgDkm▽Cm

(2)

由

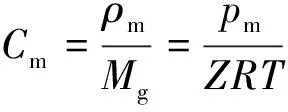
(3)

(4)

式中：Nk—— Knudsen引起的质量流量，kg(m2·s)；

Cm—— 气体的摩尔浓度，molm3；

Mg——气体的摩尔质量，kgmol；

Dkm——基岩的扩散系数[9]，m2s；

φm——基岩孔隙度；

R——理想气体分数；

Z——气体压缩因子；

T——温度，K；

c—— 趋近于1的常数[10]。

1.3 吸附-脱附作用

页岩气的吸附力取决于地层温度、压力和岩石的表明吸附能力。假定温度恒定，吸附量只是压力的函数，可采用Langmuir等温吸附模型[11-13]计算脱附量：

(5)

式中：ρs—— 页岩基质密度，kgm3；

qL—— Langmuir气体体积，m3；

pL—— Langmuir气体压力，Pa；

vstd—— 标况下气体摩尔体积，m3mol。

1.4 连续性方程

实验室研究表明，基质孔隙中的游离气来源于吸附气的解吸，裂缝中流动的气体来源于基质孔隙。根据质量守恒和达西定律，得到基岩和裂缝连续性方程。

1.4.1 基岩连续性方程

对于基质孔隙，基岩脱附气是源项，从孔隙流入裂缝的是汇项：

(6)

式中：ρm—— 气体密度，kgm3；

μm—— 气体黏度，Pa·s；

q—— 单位体积有机质脱附气量，kgm3；

pf—— 裂缝渗流压力，Pa；

Nv—— 黏性流引起的质量流量，kg(m2·s)；

Km—— 基岩视渗透率，m2。

将式(1)和式(3)带入式(6)，可得到基质孔隙连续性方程。

1.4.2 裂缝连续性方程

对于裂缝，从孔隙流入裂缝的是源项，流入井筒的是汇项：

(7)

式中：p0—— 标况下页岩气的密度，kgm3；

ρm—— 基质密度，kgm3；

φf—— 裂缝孔隙度；

ρf—— 气体在裂缝中的密度；

vf—— 气体在裂缝内的流量，m3；

Qb—— 井筒流量，m3。

式(7)经过简化，得到裂缝连续性方程：

(8)

式中：Kf—— 裂缝渗透率，m2；

μf—— 缝内气体黏度，Pa·s。

1.4.3 模型求解

将运动方程带入连续性方程，可以得到页岩气裂缝 — 基质双重介质数学模型。设置初始条件如下：

pm(x，y，t)t=0=pf(x，y，t)t=0=pi

通过有限元方法可对式(6)(7)(8)进行求解，得到简化的页岩气多级压裂水平井定压解：

(9)

s—— Laplace空间变量。

2 Knudsen扩散影响分析

页岩气的产出是游离气和吸附气解吸共同采出的结果。在给定的页岩气藏条件下，吸附对页岩气的产能影响较大，黏性流、Knudsen扩散和吸附 — 解吸附作用等渗流机制中，Knudsen扩散的影响与产能直接相关。在此重点分析扩散机制的影响。

为了进一步研究Knudsen扩散对页岩气流量的贡献，设定表1所示储层参数。

表1 储层参数表

基于以上参数，假设基质孔隙半径范围为1 ～ 1 000 nm，绘制Knudsen扩散对质量流量的贡献图(见图1)。

图1 Knudsen扩散对质量流量的贡献

由图1可以看出，Knudsen扩散对质量流量的贡献随着孔隙半径的增大逐渐减小。当孔隙半径在1 nm时，其对质量流量的贡献几乎为100%；当孔隙半径接近1 000 nm时，Knudsen扩散对质量流量的作用很小。因此，Knudsen扩散对页岩气产能的贡献不能忽略。

2.1 Knudsen扩散与压力和温度的关系

假设孔隙半径r为100 nm，不同压力和温度对Knudsen扩散的影响见图2。

图2 压力和温度对Knudsen扩散的影响

由图2可看出，压力对Knudsen扩散的影响比温度明显。Knudsen扩散的质量流量贡献，随着压力的增大而减小，随着温度的增大而增大。

2.2 Knudsen扩散判断图版

若Knudsen扩散贡献率为20%，可以考虑Knudsen扩散。以此为标准，得到Knudsen扩散判断图版(见图3)。

由图3看出，当压力小于10 MPa时，Knudsen扩散的贡献率大于20%，此时必须考虑Knudsen扩散；当孔隙半径小于120 nm时，Knudsen扩散的贡献率大于20%，必须考虑Knudsen扩散。在实践中，当图版上孔隙半径与压力的交点位于曲线的左下方时，必须考虑Knudsen扩散；当交点位于曲线的右上方时，无须考虑Knudsen扩散。

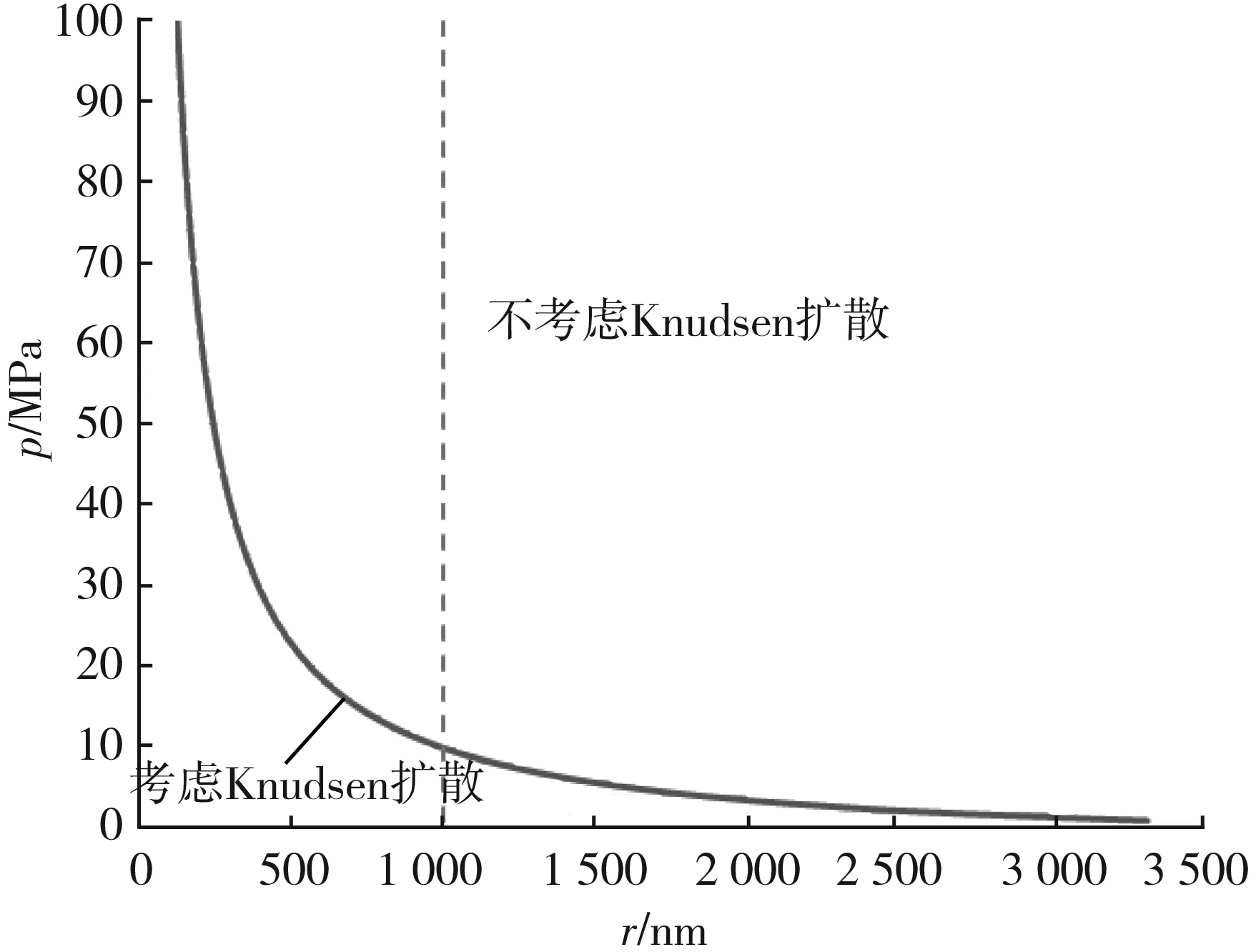
图3 Knudsen扩散判断图版

3 结 语

本次研究中，基于双重介质，建立了基质和裂缝的运动方程。考虑基质和裂缝的黏性流及Knudsen扩散作用，采用Langmuir等温吸附方程表征气体分子在基质孔隙的吸附与解吸附作用。通过Knudsen扩散的质量流量公式，分析孔隙半径、压力和温度变化对质量流量的影响。

经过研究认为，Knudsen扩散对质量流量的贡献率随着孔隙半径的增大逐渐减小。当孔隙半径在1 nm时，其对质量流量的贡献率几乎为100%；当孔隙半径接近1 000 nm时，Knudsen扩散对质量流量的作用很小。

压力对Knudsen扩散的影响比温度更明显。Knudsen扩散的质量流量贡献率，随着压力的增大而减小，随着温度的增大而增大。

当压力小于10 MPa时，Knudsen扩散的贡献率大于20%，必须考虑其影响；当孔隙半径小于120 nm时，Knudsen扩散的贡献率大于20%，必须考虑其影响。

[1] 张金川，汪宗余，聂海宽，等.页岩气及其勘探研究意义[J].现代地质，2008，22(4)：640-646.

[2] CURTIS M E,SONDERGELD C H，AMBROSE R J，et al.Microstructural investigation of gas shale in two and three dimensions using nanometer-scale resolution imaging[J].AAPG Bulletin，2012，96(4)：665-677.

[3] JAVADPOUR F, FISHER D, UNSWORTH M.Nano-scale gas flow in shale sediments[J].Journal of Canadian Petroleum Technology,2007,46(10):55-61.

[4] ROBERT G L, ROBERT M R, STEPHEN C R, et al.Morphology, genesis, and distribution of nanometer-scale pores in siliceous mudstone of the Mississippian Barnett shale[J].Journal of Sedimentary Research, 2009, 79(12):848-861.

[5] REED R M, LOUCKS R G.Imaging nanoscale pores in the Mississippian Barnett shale of the northern fort worth basin[J].AAPG Annual Convention Abstracts, 2007, 6(16):115.

[6] 樊 菁，沈 青.微尺度气体流动[J].力学进展，2002，32(3)：321-336.

[7] KAST W, HOHENTHANNER C R.Mass transfer within the gas-phase of porous media [J].International Journal of Heat and Mass Transfer,2000,43(5):807-823.

[8] OZKAN E, RAGHAVAN R. Modeling of fluid transfer from shale matrix to fracture network[G].SPE 114167,2008.

[9] FLORENCE F A, RUSHING J A, NEWSHAM K E, et al.Improved permeability prediction relations for low permeability sands [G].SPE 107954,2007.

[10] FREEMAN C M.A numerical study of microscale flow behavior in tight gas and shale gas reservoir systems[G].SPE 141125,2010.

[11] LANGMUIR I.The constitution and fundamental properties of solids and liquids：part I.solids[J].Journal of the American Chemical Society,1916,38(11):2221-2295.

[12] LANGMUIR I.The constitution and fundamental properties of solids and liquids：part II.liquids [J].Journal of the American Chemical Society,1917,39(9):1848-1906.

[13] 盛茂，李根生，黄中伟，等.页岩气藏流固耦合渗流模型及有限元求解[J].岩石力学与工程学报,2013,32(4):1896-1898.