相依网络上基于相连边的择优恢复算法∗

吴佳键1) 龚凯1)2)3) 王聪4) 王磊1)

1)(西南财经大学经济信息工程学院,成都 611130)

2)(西南财经大学,互联网金融创新及监管协同创新中心,成都 611130)

3)(西南财经大学,金融智能与金融工程四川省重点实验室,成都 611130)

4)(四川师范大学,可视化计算与虚拟现实四川省重点实验室,成都 610068)

(2017年11月24日收到;2018年1月26日收到修改稿)

1 引 言

现实世界中,基础设施网络(如通讯、交通、能源等)之间相互依赖、协同工作的情况既是一种普遍现象,也是社会各界的共识[1].对此,有研究者把这样一些存在相互依赖关系的基础网络构成的系统称为相依网络[2−4].网络间的相互依赖一方面可以提高整个系统的运转效率[5],同时也带来了意料之外的脆弱性和风险性[6].一旦这些关乎国家安全和民生的基础网络发生故障甚至瘫痪(例如2003年意大利“9.28”停电事故和2012年印度“7.31”停电事故),势必会给社会经济活动和民生造成极其严重影响.因此,如何有效地应对和控制故障传播,避免相依网络发生结构性破碎,成为复杂网络研究领域的新热点问题之一[7,8].

根据复杂网络理论[9],采用鉴别关键节点并实施预先保护是一种主流思想[10−13].对于相依网络,国内外研究者也相继提出了预先保护少数节点免受失效影响的策略,以此来减缓或阻止故障在整个系统中的传播与爆发.例如从网络中筛选出大度数或高介数节点作为不受耦合影响的自治节点[14],或是提前保护那些相连边数和相依边数都很高的节点[15],或是预先保护前5%的大度数或高Pagerank值的节点[16],文献[17]则是基于拓扑距离[18]提出了局域保护等.不过,多数研究中的故障传播和预先保护都是互不干涉的静态过程.然而,瞬息万变的真实世界更需要的是及时有效的动态应急措施,这样的措施能够在相依系统遭受故障时迅速做出响应,恢复失效节点,尽可能将损失降到最低,避免故障的升级扩大[19].

最近,文献[20]提出了一种基于相依网络的恢复模型.在该模型中,级联失效阶段和恢复节点阶段是有序交替的动态过程,其恢复的基本思想是通过定义共同边界节点(mutual boundary nodes),在每轮恢复阶段找出符合条件的共同边界节点并以一定比例实施恢复,进而遏制故障在相依网络上的扩散.当前的做法是根据随机概率进行选择,简称随机恢复算法.这种方法虽然简单直观,但显然存在很大的提升空间.考虑到现实社会中资源有限等客观因素的限制,系统遭受故障时无论采取何种应急措施都将面临择优的难题[21−23].本文利用共同边界节点在极大连通网络(giant component,GC)内外的连接边数计算定义边界节点的重要性,提出一种基于相连边的择优恢复(preferential recovery based on connectivity link,PRCL)算法.仿真结果显示,PRCL算法能够很好地鉴别恢复过程中具有重要作用的少数边界节点,有效且及时地遏制故障在网络间的级联传播.本文结构如下:介绍共同边界节点的定义,详述相依网络上的恢复模型;提出共同边界节点在极大连通网络内外连接边数的量化指标,并根据PRCL算法公式计算求出每轮恢复阶段中节点的边界重要指数,按照比例实施择优恢复;通过随机网络(ER)和无标度网络(SF)构建的ER-ER(SF-SF/ER-SF/SF-ER)相依网络上的级联仿真,分别对随机、度数中心性和局域中心性为基础的恢复算法的实施效果进行比较分析;讨论了PRCL算法的参数值.实验结果表明,PRCL算法具备恢复能力强、起效时间早且迭代步数少的优势,能够在不同的相依网络上找到对结构连通性具有重要影响作用的少数边界节点,有效地阻止故障在网络间的级联扩散,从而避免相依网络发生结构性破碎.

2 相依网络的恢复模型

最初,孤立网络上的恢复模型通常具备自发性恢复机制[24],基本思想是每隔一段时间,网络中满足条件的失效节点进行自我恢复.最近,Muro等[20]通过定义相依网络中的共同边界节点,开创性地提出一种适用于相依网络的恢复模型(本文简称恢复模型).该模型创新之处主要体现在两方面:第一,能够被恢复的节点只能是符合条件的共同边界节点;第二,相依网络的级联失效阶段和恢复节点阶段不是孤立的静态过程,而是有序交替的动态过程.

在恢复模型中,共同边界节点是指:如果网络A中的失效节点ai与极大连通网络GCA的拓扑距离l=1(即节点ai与GCA中任意节点存在连接关系),并且对应的耦合节点bj与其极大连通网络GCB的拓扑距离也同样满足l=1,那么把这对节点(ai,bj)称为共同边界节点,见图1.恢复模型中只有满足共同边界条件的失效节点才能作为候选恢复目标,这样的定义具有现实性和合理性:第一,现实世界中,当基础设施网络发生故障时,受时空等物理条件的限制,通常都是优先抢修正常区域周边的设施单位,由近到远逐步恢复;第二,如果候选恢复目标不是共同边界节点,那么就很有可能因其对应的耦合节点脱离极大连通网络而反复失效,导致这样的恢复行为没有实际意义.

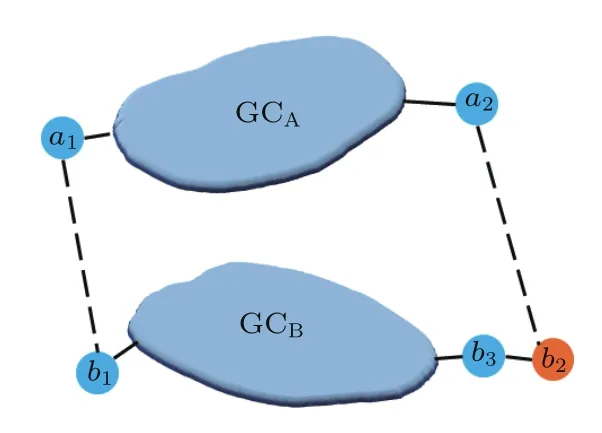
图1 相依网络的共同边界节点,节点a2对应的耦合节点b2与GCB的拓扑距离l=2,所以(a2,b2)不是共同边界节点Fig.1.Schematic demonstration of the mutual boundary of the GCs.Since the topological distance between b2and GCBis equal to 2,the point of(a2,b2)is not mutual boundary nodes.

归纳起来,恢复模型是由初始化、级联失效和实施恢复等三个阶段构成.初始阶段,随机选择网络A中比例等于1−p的节点发生故障,p是指初始正常节点比例,失效是指故障节点连同自身相连边和相依边一并从网络中移除.根据典型相依网络模型的级联规则[2],当节点满足以下条件之一就会失效:不属于极大连通网络或对应的耦合节点故障.在级联失效阶段,当网络A碎裂成多个网络时,不属于极大连通网络GCA的节点随即失效,这些故障节点通过相依边的作用导致网络B中的耦合节点也发生级联故障,进而改变网络B的连通性,且不属于GCB的节点失去功能.反过来,网络B中失效节点同样通过相依边的耦合关系造成网络A中的节点失效,进一步导致网络A破碎.重复迭代直至没有新增失效节点.显然,初始阶段和级联失效阶段正是典型相依网络的动力学过程.在此,引入恢复机制.简单地说,在迭代步数n>0时,网络A将自身故障传递到网络B.接着,网络B因其受到耦合关系的牵连,导致网络内某些节点脱离GCB,同时又造成网络A上的耦合节点失效.但不同的是,在网络B将故障传递回网络A之前,恢复机制会介入并找出当前的共同边界节点,按比例实施恢复.实施结束后,网络B继续将故障传递回网络A,见示意图2.

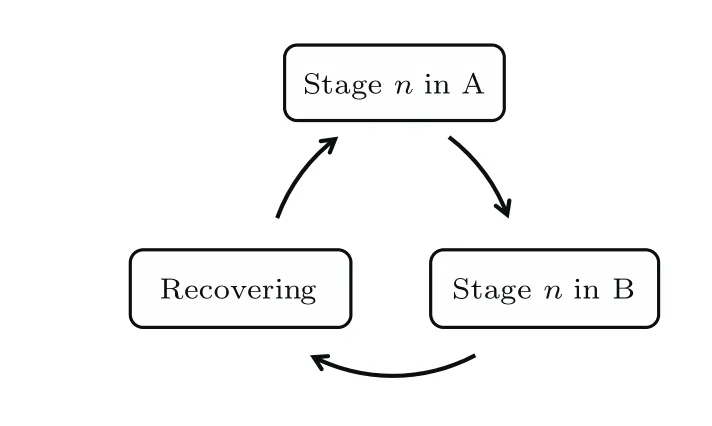
图2 相依网络的恢复模型Fig.2.Schematic model of the failures-recovery in interdependent networks.

具体逻辑流程如下.

I.Stagenin A

1)如果网络A中正常节点ai的耦合节点bi在n−1步时已失效,则ai失效;

2)当前已脱离极大连通网络GCA的节点都失效.

II.Stagenin B

3)如果网络B中正常节点bj的耦合节点aj在步骤2)失效,则bj失效;

4)当前已脱离极大连通网络GCB的节点都失效.

III.Recovering

5)找出所有的共同边界节点,按照一定比例λ(这里指恢复过程中边界节点的恢复比例)进行选择恢复,当前采取的做法是按随机概率恢复;凡是被恢复的节点,其自身与极大连通网络内的所有连边一并恢复,并且恢复与本轮其他被恢复节点的原有连边;

6)重复步骤1)—5),一旦当前网络达到稳态(不再新增失效节点),整个恢复模型的动力学过程终止,此时网络是剩余的极大连通网络.

3 基于相连边的择优恢复算法

在恢复模型中,随机恢复算法之所以有效是因为共同边界特性:边界节点与极大连通网络的拓扑关系确保恢复行为能够最大程度地增强剩余网络的结构鲁棒性,同时,利用相依关系的对称性,实施恢复又可以最大限度地避免被恢复节点受相依边的耦合作用导致无效恢复.然而,从现实角度考虑,相依系统遭受故障时无论采取何种应急措施都会面临选择谁实施恢复的难题,这是由资源有限等客观因素所决定的.例如真实世界中防控疾病传播要重点关注高危人群[25]、阻断互联网谣言散播需要重点监管意见领袖[26,27]等.所以,采取择优算法相比随机方法而言,具备更广的适用性和更强的指导性.

一般地,择优选择首先要考虑的是怎样合理地利用结构特征对节点进行有效鉴别从而发现重要节点[28].受文献[29]的启发,可以发现边界节点的相连边在恢复过程中存在两种情况:与当前极大连通网络内的正常节点存在原有连接(见图3蓝色虚线),或是与当前极大连通网络外的失效节点存在原有连接(见图3黑色虚线).仔细分析,边界节点与极大连通网络内相连边数量的多少,意味着恢复该节点后的极大连通网络内节点平均度的增减变化,而已知节点平均度与网络鲁棒性呈正相关[30,31].另一方面,边界节点与极大连通网络外的相连边数量又意味着该节点在原始网络上的结构连通性或是局限性[32],这类连边数越多,说明后续恢复阶段的候选目标数就越多,重要边界节点被选中的潜在性也就越高.可想而知,恢复模型上边界节点的重要性既依赖于该节点与极大连通网络内的连接关系,也依赖与极大连通网络外的连接关系,所以,衡量边界节点重要性时需要综合考虑上述两类相连边以及它们在恢复作用上的比重关系,这不同于以往研究工作将连边数最多的节点简单地定义成重要节点的思想[33].本文利用边界节点在极大连通网络内外的连接边数计算边界节点的重要性,提出PRCL算法.这里用符号I代表恢复模型中边界节点的边界重要指数.PRCL算法的具体步骤如下.

1)迭代步数n时,在恢复阶段找出相依网络上所有的共同边界节点.

2)遍历网络A上的边界节点,按照如下规则计算求出每个节点的边界重要指数:

①计算边界节点vi与当前极大连通网络GCA的失效连边数,即边界节点vi与极大连通网络内正常节点存在原有连边的数量,用符号表示;

②计算边界节点vi与极大连通网络GCA外失效节点存在原有连边的数量,用符号表示;3

③根据(1)式求出节点vi的边界重要指数,

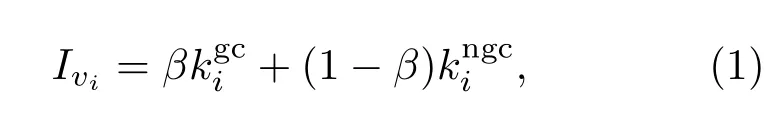
式中参数β(β∈[0,1])代表两类相连边在计算边界节点重要性时的比重关系.为了便于计算,用参数f=β/(1−β)来量化这两类相连边的比重关系.如果参数f等于1,即β取值等于0.5时,说明极大连通网络内的相连边与极大连通网络外的相连边就衡量边界节点的重要性而言同样重要.有关参数讨论请见后文的算法分析.在此,简单且不失一般性,本文参数f默认值为2.

3)网络A遍历结束后,按照恢复比例λ,根据边界重要指数进行降序恢复.一旦网络A的边界节点恢复正常,网络B对应的耦合节点也立刻恢复.见图3.

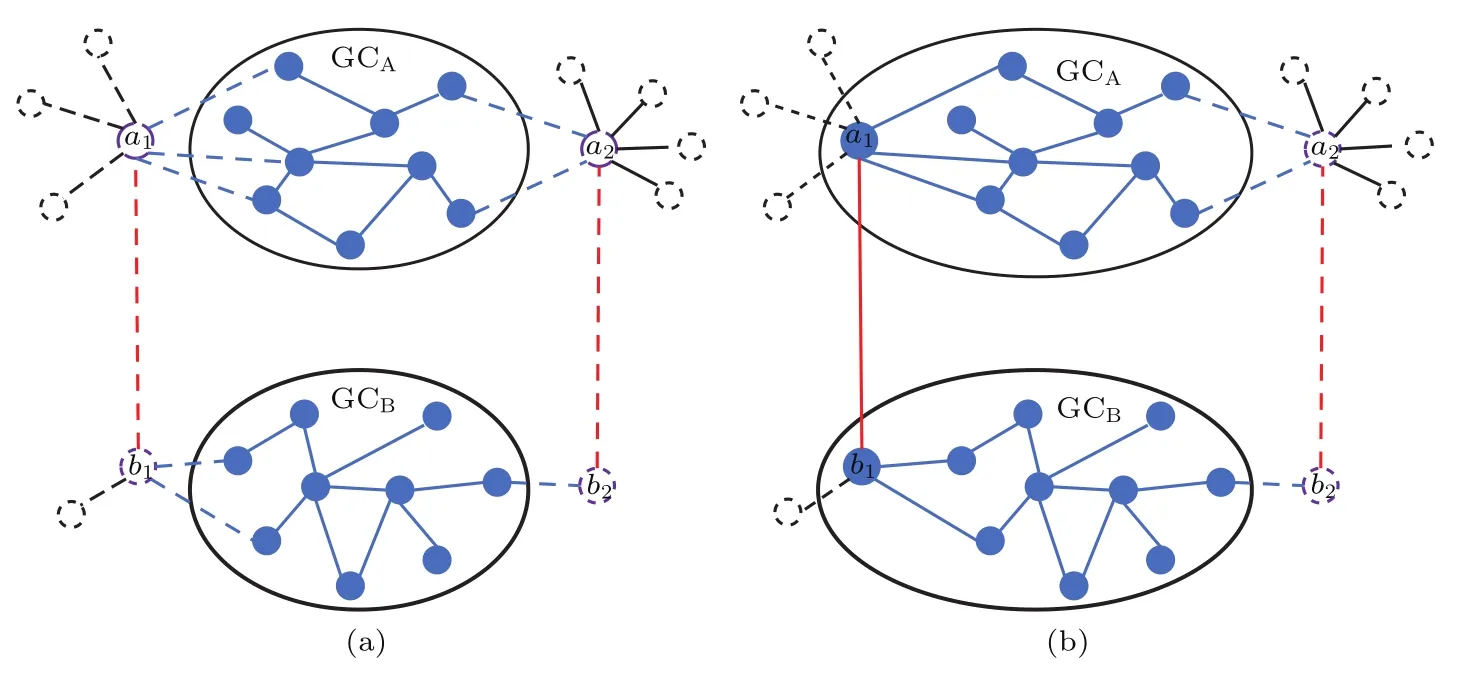
图3 基于相连边的择优恢复过程,(a)节点对(a1,b1)和(a2,b2)是两组共同边界节点,节点a1和a2都有6条相连边,其中节点a1的kgc=3且kngc=3;(b)依据计算公式可知I(a1)=9/3,同理得知I(a2)=8/3,因而优先恢复a1和耦合节点b1,然后修复(a1,b1)的相依边以及与其他正常节点的连接关系Fig.3.Schematic illustration of the PRCL strategy:(a)Two pairs of mutual boundary nodes((a1,b1)and(a2,b2))are shown;(b)by counting the number of first-type and second-type connectivity links of node a1,kgc=3 and kngc=3,after calculating the boundary importance index with f=2,then I(a1)=9/3;in the same way,I(a2)=8/3,so two interdependent nodes a1and b1are preferential repaired,all their connections with the GCs and all links between reactivated failure nodes are restored.

为了比较分析PRCL算法的恢复效果,以经典复杂网络理论中常见的三种中心性指标为基准算法:随机(random,RR)、度数中心性(degree,PRD)和局域中心性(local,PRL).这里,RR算法是指通过随机方式选取边界节点进行恢复,PRD算法是指优先选取大度的边界节点进行恢复[34],PRL算法是指根据边界节点的原有邻居拓扑关系优先选择局域中心性最高的边界节点进行恢复[35].

4 仿真结果与分析

为了检验恢复算法的有效性,本文利用ER随机网络[36]和无标度网络[37]构建同构相依网络和异构相依网络.这四类网络(ER-ER/SF-SF/ERSF/SF-ER)表征相依网络不同的结构特征,能够更全面地评估PRCL算法的恢复效果.参照文献[20]的取值和方法,子网络节点规模等于10000,相依网络规模N=20000,节点平均度⟨k⟩=5.根据以上参数,利用基于渗流理论[38]的随机故障模型进行仿真模拟,数据均为独立重复104次的平均值.

图4描述的是边界节点恢复比例λ=3%时,存在极大连通网络的概率随初始正常节点比例的变化情况.横坐标p表示初始时网络正常节点的比例,纵坐标P∞表示相依网络遭受随机故障后存在极大连通网络的概率[2].本文认定相依网络遭受故障但经修复达到稳态后,如果子网络A的剩余极大连通网络节点数NGCA>2,并且子网络B的剩余极大连通网络的节点数NGCB>2,则视为存在;否则视作崩溃.在此,P∞的具体计算是统计存在极大连通网络(NGCA=NGCB>2)的试验次数占总试验次数的比例.图示方块(圆圈/菱角/十字)表示采用PRCL算法(PRD/PRL/RR)的恢复情况,P∞值越大说明网络鲁棒性越强,也就说明恢复算法在相同p值时的恢复效果越好.观察图4(a)所代表的ER-ER网络可见,PRCL算法实施恢复后的效果十分突出,其次是PRD算法和PRL算法,相比择优选择的结果来看,RR算法的恢复效果最差.进一步观察图4(b)、图4(c)和图4(d),可见PRCL算法在异构或是同构的相依网络上均表现出非常明显的优势.而当λ取值等于5%(图5)和10%(图6)的情况时,PRCL算法在恢复效果上的有效性仍然保持不变.甚至在λ取值过大时(λ=30%,图7),较高的恢复比例会造成恢复节点数太多从而模糊算法间的效果差异,例如PRD和PRL在多数情况下就因交织纠缠而难以辨别,但即便如此,PRCL算法也依然表现出微弱性优势.综上可知,PRCL算法能够更好地鉴别相依网络恢复阶段具有重要作用的少数边界节点,有效地遏制住故障在网络间的级联扩散.

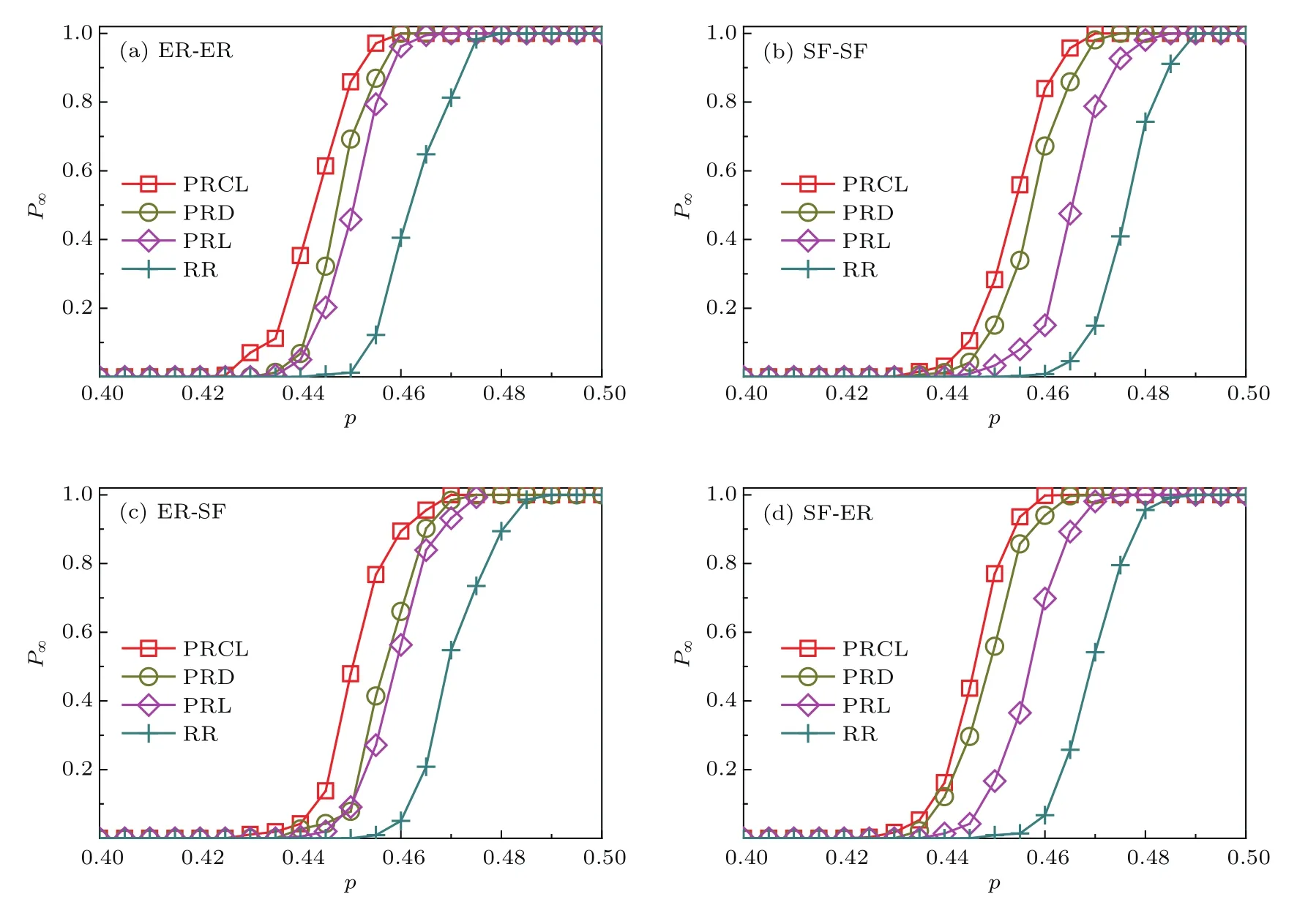
图4 边界节点恢复比例λ=3%时,存在极大连通网络的概率P∞随初始网络正常节点比例p的变化Fig.4.Probability of existence of the giant connected component,P∞,as a function of p with λ =3%.

图8 比较分析的是PRCL算法与其他恢复算法在迭代步数(number of iteration steps,NOI)方面的表现情况.NOI表示遭受随机故障时相依网络达到稳态所经历的迭代步数[2,39].对于恢复算法而言,图中迭代步数(NOI)峰值是指实施恢复后网络达到稳态时所需的最大迭代步数.图8(a)中,PRCL算法的NOI峰值最小(NOI为6.803),低于PRD(NOI为6.962)、PRL(NOI为7.113)和RR算法(NOI为7.322),同样的情况也出现在其他相依网络上,如图8(b)、图8(c)和图8(d)所示.直观可见,相比其他算法,PRCL算法能够在最少迭代步数内有效地控制住故障在相依网络上的传播扩散.另一方面,观察四条曲线发现,PRCL算法在NOI峰值处的正常节点比例p的数值明显低于PRD,PRL和RR算法,例如在图8(a),PRCL算法NOI峰值对应的pNOI=0.43,低于PRD(pNOI=0.435),PRL(pNOI=0.435)和RR算法(pNOI=0.45),这种优势在其他相依网络中(图8(b)、图8(c)、图8(d))同样存在.可见,PRCL算法施加于相依网络后发挥恢复作用的起效时间最早,具有很强的及时性.整体来看,PRCL算法在不同的相依网络上都表现出起效时间早且迭代步数少的优势,因而能够及时地阻断故障在网络间的级联扩散.

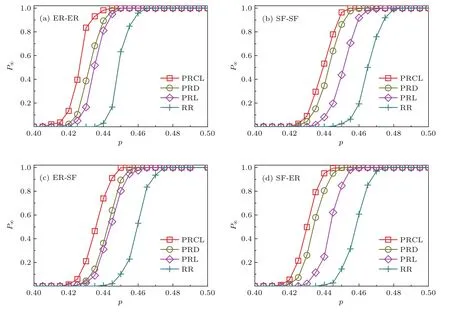
图5 边界节点恢复比例λ=5%时,存在极大连通网络的概率P∞随初始网络正常节点比例p的变化Fig.5.Probability of existence of the giant connected component,P∞,as a function of p with λ =5%.

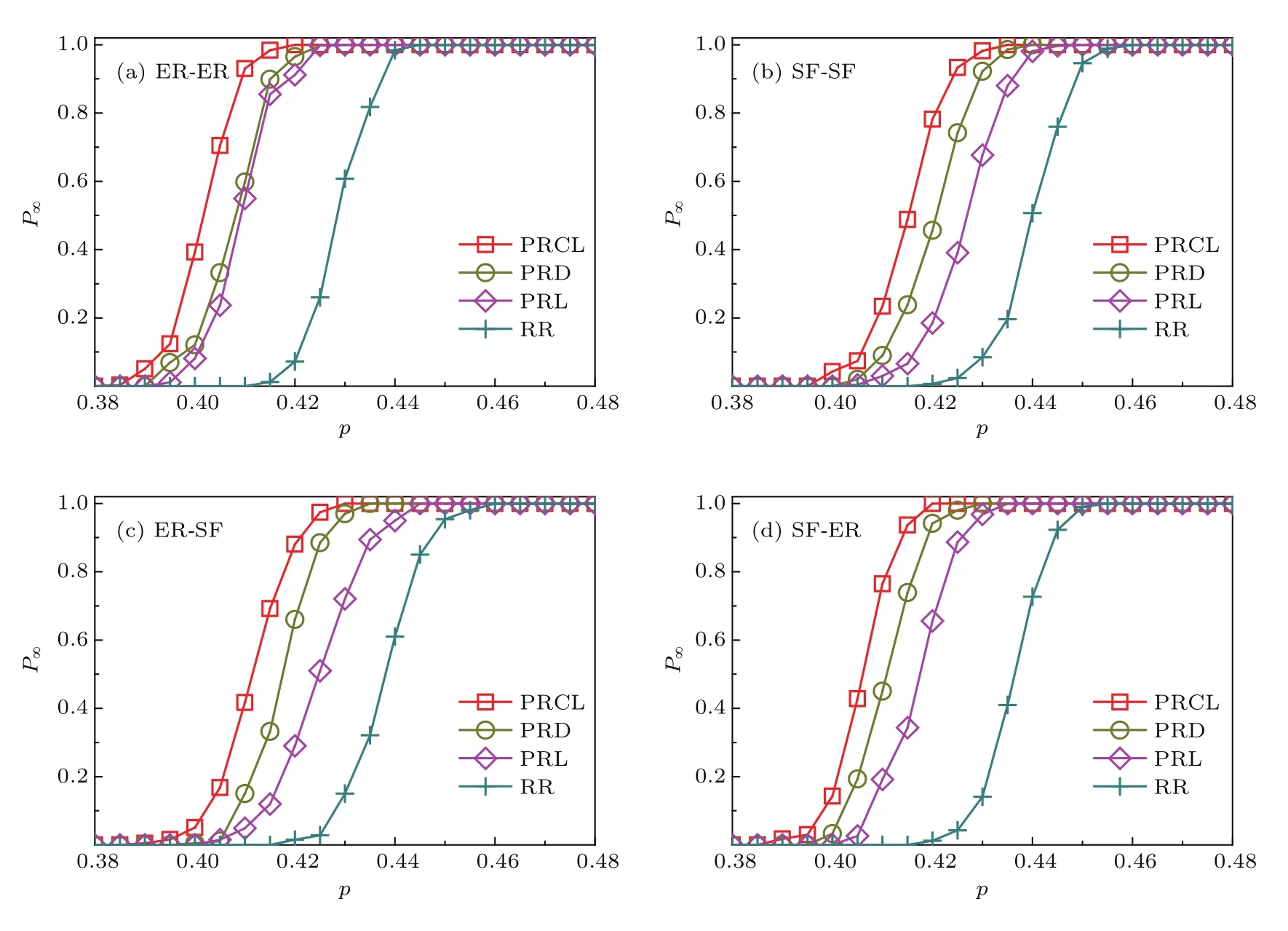
图6 边界节点恢复比例λ=10%时,存在极大连通网络的概率P∞随初始网络正常节点比例p的变化Fig.6.Probability of existence of the giant connected component,P∞,as a function of p with λ =10%.

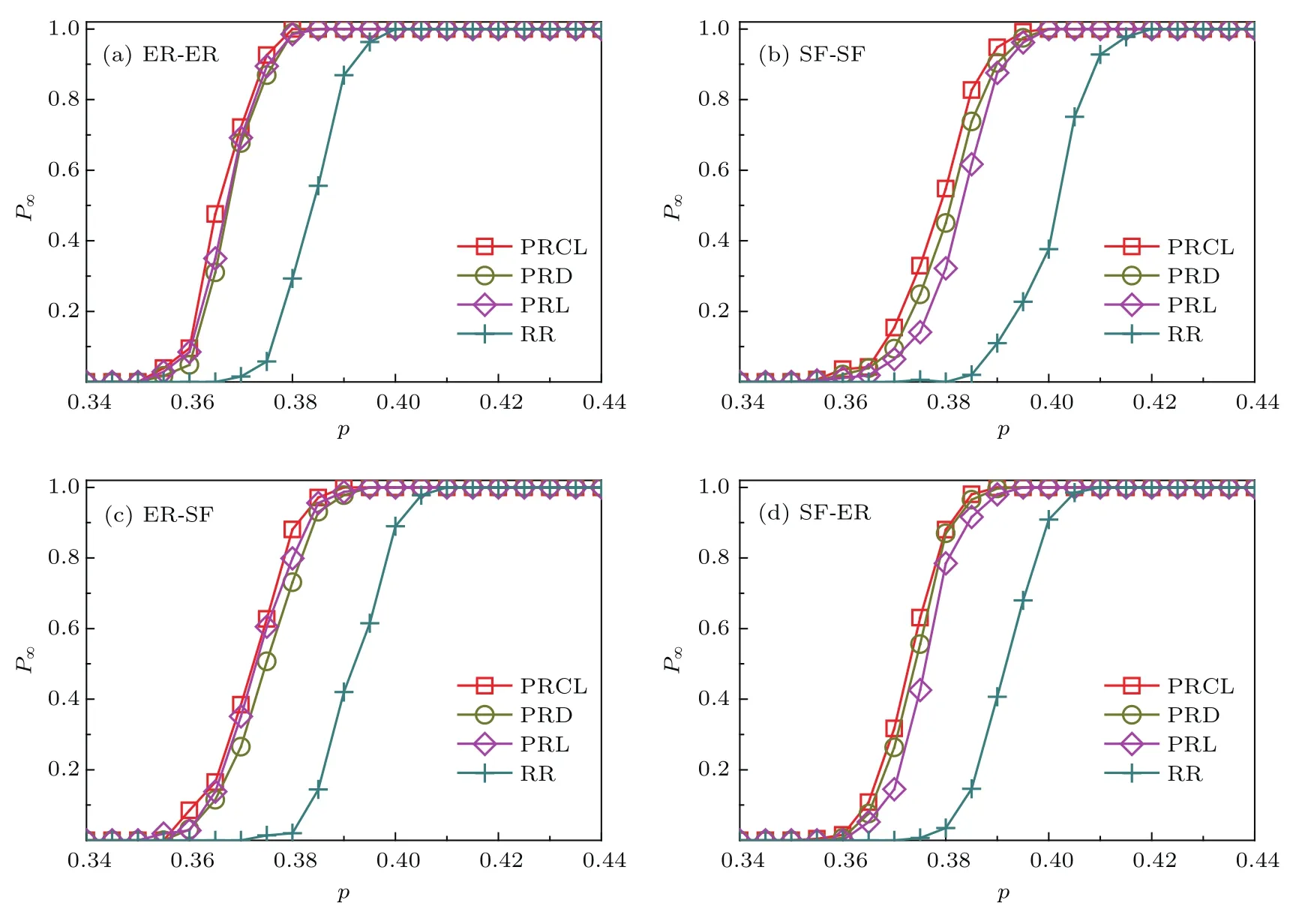
图7 边界节点恢复比例λ=30%时,存在极大连通网络的概率P∞随初始网络正常节点比例p的变化Fig.7.Probability of existence of the giant connected component,P∞,as a function of p with λ =30%.

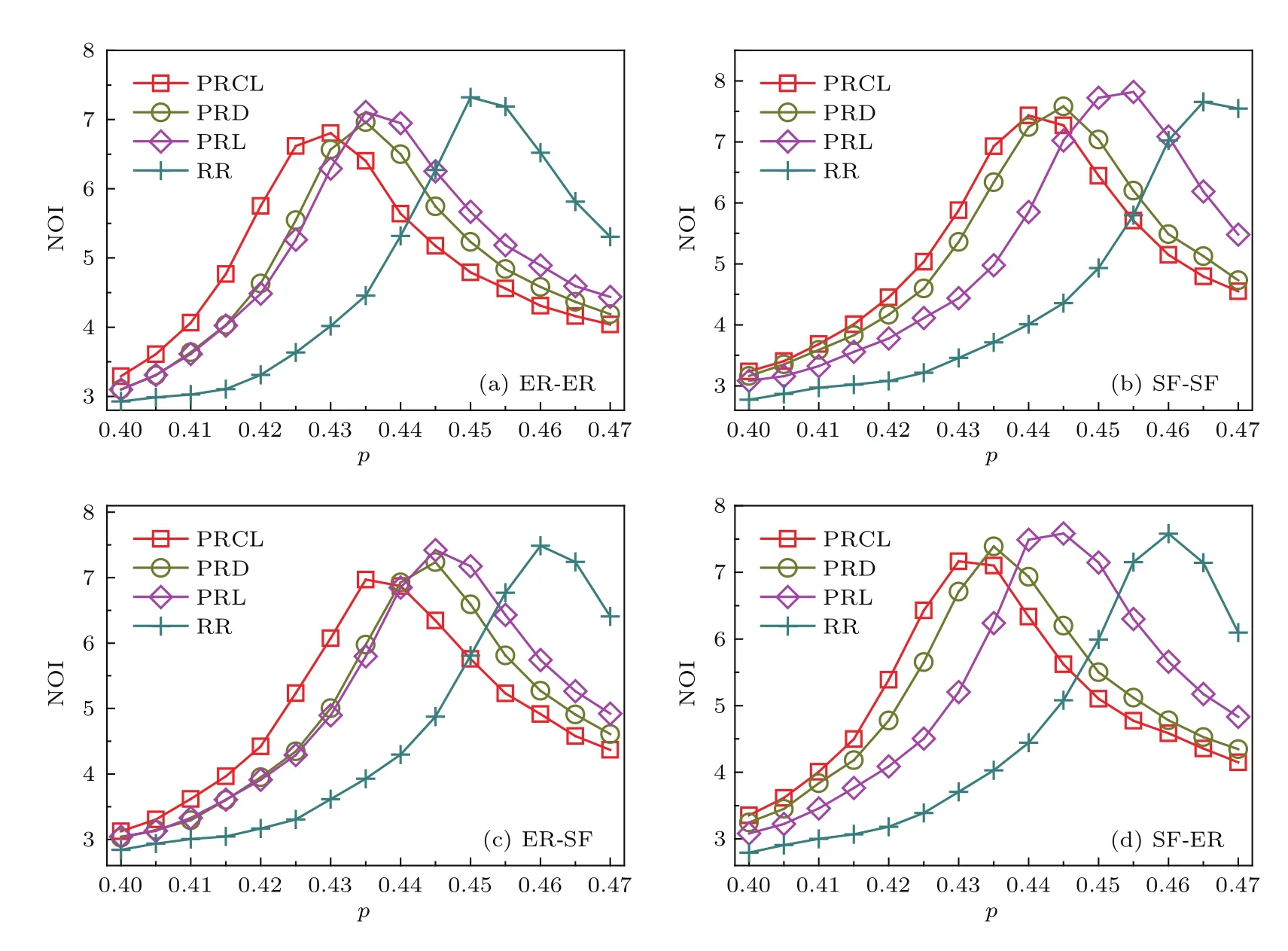
图8 迭代步数NOI随初始正常节点比例p的变化,边界节点恢复比例λ=5%Fig.8.The number of iteration steps(NOI)in the steady state as a function of p with λ=5%.

根据文献[20]中的分析可知,施加恢复算法后相依网络存在三个相图区域:崩溃、恢复和未崩塌.当给定恢复比例λ时,三个区域实质上对应的是正常节点比例p的三个区间.崩溃区域是指正常节点比例p太低造成整个系统彻底破碎,这种情况已经超出恢复算法的有效范围;恢复区域是指受惠于恢复算法的有效作用,网络遭受故障后结构可能有破损但不会完全崩塌;未崩塌区域是指正常节点比例p太高,这种状态下即便不采取恢复,网络也不会出现结构性崩塌.显而易见,在恢复区域内,网络结构完整程度的差异在一定程度上反映出不同算法在网络抗毁性和鲁棒性方面的提升效果,同时也反映算法的优异性.对此,我们利用恢复鲁棒系数 (recovery robustness,Rrc)[16]来衡量实施恢复算法后在恢复区域内的网络鲁棒性.Rrc计算公式如下:

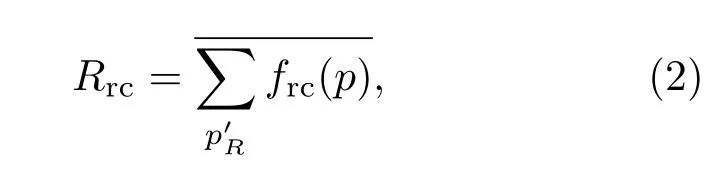
表2描述了当恢复比例λ=5%时,实施不同恢复算法后网络达到稳态时极大连通网络的节点平均度⟨k⟩的情况.在这里,如果正常节点比例p取值太低,整个网络会因失效节点过多而完全破碎,如果取值太高又无法引起传播.参考文献[20]里相图中的恢复区域,选取ER-ER(SFSF/ER-SF/SF-ER)网络的正常节点比例p=0.46(0.47/0.47/0.47).观察表2,PRCL算法在ERER(SF-SF/ER-SF/SF-ER)网络实施恢复后,网络达到最终稳态时的⟨k⟩=3.1311(3.3184/3.1947/3.2979),不仅高于同类择优算法PRD和PRL的情况,相比RR算法的⟨k⟩更是提升了24.74%(30.84%/24.81%/28.84%).进一步观察可见,与相依网络遭受第一轮故障但尚未实施恢复的初始状态相比,采用随机方法的RR算法实施后的ER-ER(SF-SF/ER-SF/SF-ER)网络的⟨k⟩降低了4.05%(2.27%/3.51%/1.31%),也就是说,RR算法并没有提高剩余网络的结构连通性.相反,采用择优方法的PRCL算法实施恢复后,与相依网络遭受第一轮故障时初始状态相比,最终稳态的ER-ER(SF-SF/ER-SF/SF-ER)网络的⟨k⟩提高了19.69%(27.86%/20.44%/27.15%).总之,相比其他恢复算法,PRCL算法发现的边界节点能够明显地增强剩余网络的结构连通性,有效地控制故障恶化避免结构破碎.

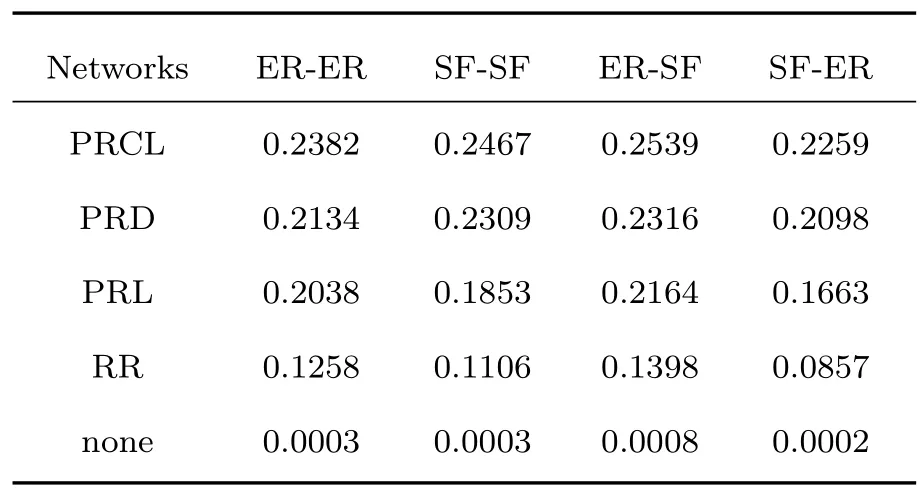
表1 恢复算法施加在相依网络时的恢复鲁棒系数Rrc,边界节点恢复比例为λ=5%Table 1.Comparisons of the recovery robustness Rrc obtained by recovering 5%mutual boundary nodes with dif f erent strategies.

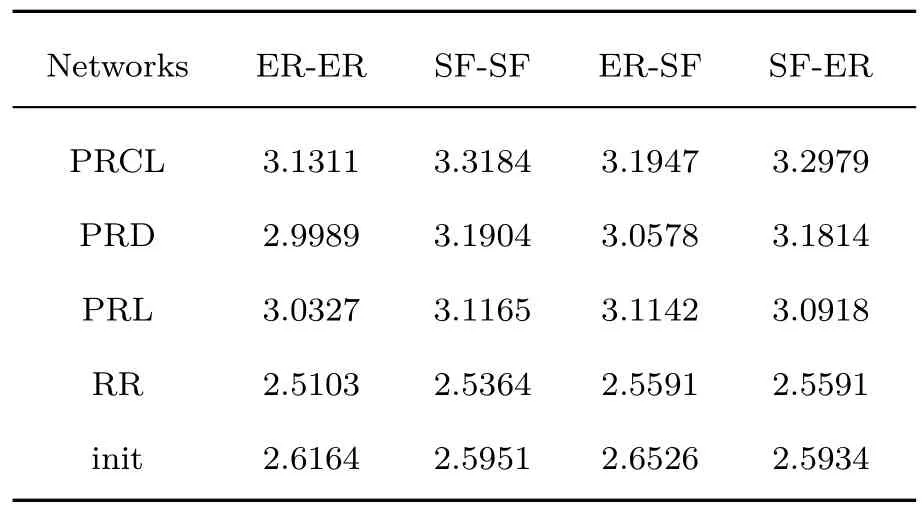
表2 实施恢复算法后极大连通网络的节点平均度⟨k⟩,边界节点恢复比例λ=5%Table 2.Comparisons of average degree of the steady state of the giant connected component network by recovering 5%mutual boundary nodes with dif f erent strategies.

5 算法讨论

代表两类相连边比重关系的参数f是影响PRCL算法在相依网络上恢复效果的关键因素之一,在此讨论算法参数f取值与恢复效果的情况,如图9所示.纵坐标pc表示存在极大连通网络的概率大于或等于50%时正常节点比例的阈值[20],pc越低说明恢复效果越好.观察ER-ER(SF-SF/ER-SF/SF-ER)相依网络,参数f与阈值pc整体呈现两端高中间低的U形现象:1)参数f=1的恢复效果在所有网络都最差,pc=0.4319(0.443/0.4426/0.4337).该现象说明边界节点进行择优恢复时,两类相连边发挥的影响作用不能相提并论;对于极大连通网络内的相连边,其实质作用是在本轮恢复阶段及时地增强剩余网络的结构连通性;反观极大连通网络外的相连边,可以在后续恢复阶段增加潜在恢复目标的数量,间接提高重要边界节点被优先恢复的概率,所以极大连通网络内的相连边相对更重要;2)当参数f=∞时,也是当β=1时(只考虑边界节点与极大连通网络内的相连边,完全忽略与极大连通网络外的相连边),参数f与pc未呈线性负相关,反而出现pc显著变大的上扬现象(0.4257/0.4386/0.4359/0.4297),该现象从侧面反映出边界节点的两类相连边虽各有不同,但只有综合考虑才能最大程度地发挥恢复效果;3)当参数f取值有限且f>2时,f在一定取值范围内与pc呈现出近似线性反比的现象,但整体而言参数f与阈值pc之间不呈线性负相关,例如f∈[2,8]([2,6]/[2,6]/[2,6])局部范围时,f越大pc越低,而随着f>8(6/6/6),pc出现了时高时低的交替变化.

进一步分析,参数f存在一个近似最优值能使pc达到相对的最低点,例如f=8(6,6,6)的ER-ER网络(SF-SF,ER-SF,SF-ER)的pc值降到相对最低.不过,f最优值的选定有可能需要深入研究相依网络的子网结构与节点平均度对参数f造成的影响.

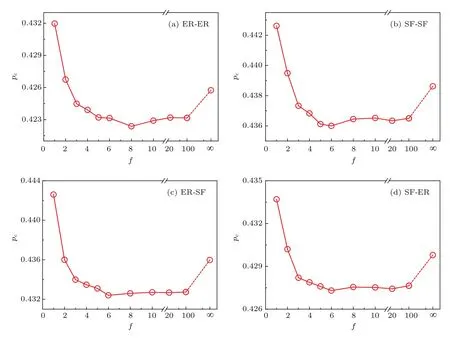
图9 存在极大连通网络的正常节点比例阈值pc随参数f的变化,边界节点恢复比例λ=5%Fig.9.The critical point pcfor dif f erent parameters of f with λ=5%under PRCL.

6 结论与展望

受客观因素的影响,相依网络遭受随机故障时选择谁优先进行恢复是我们面临的现实性难题.考虑到恢复模型中边界节点的相连边存在两种情况:与当前极大连通网络内的正常节点存在原有连接,或是与当前极大连通网络外的失效节点存在原有连接.在此,基于相依网络的恢复模型,本文利用边界节点在极大连通网络内外的连接边数计算边界节点的重要性,提出一种基于相连边的择优恢复算法(PRCL算法).

通过由ER网络和无标度网络构建的ERER(SF-SF/ER-SF/SF-ER)相依网络的随机故障级联仿真实验表明,PRCL算法能够更好地鉴别相依网络恢复阶段具有重要作用的边界节点,有效地遏制故障在网络间的级联扩散;同时,利用NOI迭代步数等指标表明PRCL算法具备起效时间早和迭代步数少的优势.另外,本文利用恢复鲁棒系数进行对比分析,发现施加PRCL算法后相依网络具有更好的结构完整性,体现了本算法的优异性和适用性.而极大连通网络节点平均度的比较结果也进一步说明PRCL算法可以增强结构连通性.最后,通过算法分析发现,算法参数f与恢复效果不呈线性正相关.当参数f取值有限且f>2时,PRCL算法发挥出较好的恢复效果.相比而言,参数f=1在所有网络中的恢复效果都相对较差,而参数f→∞时,PRCL算法也没有表现出更好的恢复效果.上述结果进一步说明PRCL算法的核心问题,即恢复模型的两类相连边发挥的影响作用各有不同,合理地利用两类相连边的比重关系能够最大程度地增强相依网络的恢复能力.

本文利用边界节点与极大连通网络内外连接关系的思想对恢复模型中边界节点的重要性进行度量,进而择优恢复相依网络上的重要节点.该研究工作对于现实世界中相依系统遭受随机故障时的应急决策和实施行为具有科学的指导意义和实际的可操作性,同时,也为深入研究相依网络抗毁性等后续工作提供了借鉴.

[1]Vespignani A 2010Nature464 984

[2]Buldyrev S V,Parshani R,Paul G,Stanley H E,Havlin S 2010Nature464 1025

[3]Gao J X,Buldyrev S V,Stanley H E,Havlin S 2012Nat.Phys.8 40

[4]Chen S M,Lü H,Xu Q G,Xu Y F,Lai Q 2015Acta Phys.Sin.64 048902(in Chinese)[陈世明,吕辉,徐青刚,许云飞,赖强2015物理学报64 048902]

[5]Rinaldi S M,Peerenboom J P,Kelly T K 2001IEEE Contr.Syst.21 11

[6]Morris R G,Barthelemy M 2013Sci.Rep.3 2764

[7]Liu L J,Yin Y F,Zhang Z H,Malaiya Y K 2016Plos One10 e0164777

[8]Korkali M,Veneman J G,Tivnan B F,Bagrow J P,Hines P D H 2017Sci.Rep.7 44499

[9]Wang X F,Li X,Chen G R 2012Network Science:An Introduction(Beijing:Higher Education Press)(in Chinese)[汪小帆,李翔,陈关荣 2012 网络科学导论(北京:高等教育出版社)]

[10]Cohen R,Erez K,Ben-Avraham D,Havlin S 2001Phys.Rev.Lett.86 3682

[11]Albert R,Albert I,Nakarado G L 2004Phys.Rev.E69 025103

[12]Gong K,Tang M,Hui P M,Zhang H F,Younghae D,Lai Y C 2013Plos One8 83489

[13]Zhang Z K,Liu C,Zhan X X,Lu X,Zhang C X,Zhang Y C 2016Phys.Rep.65 1

[14]Schneider C M,Yazdani N,Araújo N A M,Havlin S,Herrmann H 2013Sci.Rep.3 1969

[15]Du R J,Dong G G,Tian L X,Liu R R 2016Physica A450 687

[16]Gong M G,Ma L J,Cai Q,Jiao L C 2015Sci.Rep.5 8439

[17]Wang J D,Lao S Y,Ruan Y R,Bai L,Hou L L 2017Appl.Sci.7 597

[18]Shang Y L 2016Sci.Rep.6 30521

[19]Shekhtman L M,Danziger M M,Havlin S 2016Chaos Solition.Fract.90 28

[20]Muro M A D,Rocca C E L,Stanley H E,Havlin S,Braunstein L A 2016Sci.Rep.6 22834

[21]Schneider C M,Moreira A A,Andrade J S,Havlin S,Herrmann H J 2011Proc.Natl.Acad.Sci.USA108 3838

[22]Huang X Q,Gao J X,Buldyrev S V,Havlin S,Stanley H E 2011Phys.Rev.E83 065101

[23]Hu F Y,Yeung C H,Yang S N,Wang W P,Zeng A 2016Sci.Rep.6 24522

[24]Majdandzic A,Podobnki B,Buldyrev S V,Kenett D Y,Havlin S,Stanley H E 2013Nat.Phys.10 34

[25]Liu J G,Lin J H,Guo Q,Zhou T 2016Sci.Rep.6 21380

[26]Weng J S,Lim E P,Jiang J,He Q 2010Proceedings of the Third ACM International Conference on Web Search and Data Mining(New York:ACM Press)pp261–270

[27]Liu C,Zhang Z K 2014Commun.Nonlinear.Sci.19 896

[28]Ren X L,Lü L Y 2014Chin.Sci.Bull.13 1175(in Chinese)[任晓龙,吕琳媛 2014科学通报 13 1175]

[29]Liu R R,Li M,Jia C X,Wang B H 2016 Sci.Rep.6 25294

[30]Sun S W,Wu Y F,Ma Y L,Wang L,Gao Z K,Xia C Y 2016 Sci.Rep.6 32983

[31]Wang X Y,Cao J Y,Qin X M 2016 Plos One 11 e0160545

[32]Boccaletti S,Bianconi G,Criado R,del Genio C I,Gómez-Gardeñes J,Romance M,Sendiña-Nadal I,Wang Z,Zanin M 2014 Phys.Rep.544 1

[33]Valdez L D,Macri P A,Braunstein L A 2014 J.Phys.A:Math.Theor.47 055002

[34]Freeman L C 1979 Social Networks 1 215

[35]Chen D B,Lü L Y,Shang M S,Zhang Y C,Zhou T 2012 Physica A 391 1777

[36]Erdös P,Rényi A 1959 Publ.Math.Debrecen 6 290

[37]Newman M E 2003 SIAM Rev.45 167

[38]Radicchi F 2015 Nat.Phys.11 7

[39]Liu R R,Jia C X,Zhang J L,Wang B H 2012 J.Univ.Shanghai Sci.Technol.34 235(in Chinese)[刘润然, 贾春晓,章剑林,汪秉宏2012上海理工大学学报34 235]