有界大洋对纬向风强迫的响应及共振∗

张东凌1) 卢姁2)3) 张铭3)

1)(中国科学院大气物理研究所,国际气候与环境科学中心,北京 100029)

2)(中国人民解放军61741部队,北京 100094)

3)(解放军理工大学气象海洋学院,大气环流与短期气候预测实验室,南京 211101)

(2017年10月13日收到;2017年12月11日收到修改稿)

1 引 言

20世纪90年代后,10年及以上年代际尺度的海洋气候变化已成为气候学中的热点问题.太平洋年代际振荡(Pacific decadal oscillation,PDO)是北太平洋海表面温度(sea surface temperature,SST)年代际时间尺度上气候变率的强信号[1,2],国内外已有许多研究[3−7],其可直接造成太平洋及其周边地区大气环流的年代际变化[8].然而PDO仍不能完全解释东北太平洋中盐度、营养物、叶绿素及鱼储量等的年代际变化.为此,2008年,Lorenzo等[9]对东北太平洋海域的海表面高度(sea surface height,SSH)定义了一个新的气候模态,即北太平洋流涡振荡(North Pacific gyre oscillation,NPGO),它能很好地反映风应力和海表面盐度距平的变化,且与东北太平洋生物变量趋势有很大相关性.因SST和SSH的变化趋势有较高相关性[10],故也可用SST的年代际变化来表示NPGO模态.PDO和NPGO作为北太平洋的主要气候模态,已受到人们的广泛重视[11−13].PDO和NPGO模态既是海气相互作用的产物,又受全球变暖影响,同时也会改变北太平洋海洋要素的分布,并对大气环流有影响.研究认为北太平洋PDO模态与大气阿留申低压异常有关[14],北太平洋NPGO模态则与大气的北太平洋涛动(North Pacific oscillation,NPO)有关[15].中纬度西风急流造成近地面西风应力,其强迫会使大洋上层流动发生响应.风应力驱动上层大洋的理论早在20世纪50年代就已被提出,然而直到目前,海洋对风应力响应的研究仍很受重视[16−21].北太平洋主要气候模态PDO和NPGO与风应力关系密切.

吕庆平等[22]曾对冬季北太平洋上层流场异常做过复经验正交函数(empirical orthogonal function,EOF)分解,发现第一、二模态的时间系数场与北太平洋表面温度异常(sea surface temperature anomaly,SSTA)空间场的回归系数场分别与PDO,NPGO模态的空间场结构相似,第一模态有20 a的年代际变化,第二模态有18,14 a的年代际变化.张东凌等[23]对冬季北太平洋大气风场和大洋流场做过联合复EOF分解,发现其第一、二模态的时间系数与PDO,NPGO指数有较高相关性,且第一模态有22,14 a的年代际变化,还有明显的7 a的年际变化,第二模态有17,11 a的年代际变化.以上这些年代际变化中第一、二模态均与PDO模态的年代际变化(准20 a,见文献[3])和NPGO的年代际变化(准13 a,见文献[24])相近;在以上吕庆平和张东凌的复EOF分解的海洋流场上,第一模态的空间场都表现为在整个北太平洋有洋盆尺度气旋式旋转的大洋环流,在日本本州岛以东有一个椭圆形流涡;而第二模态的空间场也都表现为在北太平洋中高纬度和中低纬度分别有洋盆尺度的气旋式环流和反气旋环流,在日本本州岛以东也有气旋流涡出现;张东凌的工作还发现,堪察加半岛东南海域还有反气旋流涡存在[22,23].吕庆平和张东凌都将流场异常的第一、二模态分别对应为PDO和NPGO的流场模.路凯程等[25]对北太平洋1,4,7,10月份风应力与流场异常做过联合EOF分解,并给出了第一模态的结果,发现其时间系数1,4,7,10月份分别有18,15,20,15,17,14,19 a的年代际变化及5,5,8,3 a的年际变化.

文献[23—25]的结果是对北太平洋的实际资料进行诊断分析后得到的,虽然揭示了很多事实,但是有关这些事实的原因却难以从动力学上做出明确解释.如:纬向风强迫真的可以产生PDO和NPGO的流场模吗?为何北太平洋的年际变化和年代际变化都出现在那几个有限的周期附近?这些周期与大洋自身的尺度有什么关系?大洋是如何对外强迫风场做出响应的?大洋能够与风场强迫产生共振吗?这些都是重要的问题,目前也都没有公认的准确答案.为此本文利用约化重力准平衡线性海洋模型,对有界大洋对纬向风强迫的响应做了动力学解析研究,并做了讨论,试图回答以上问题.

2 数学模型

本文所用的数学模型为中纬β通道中的约化重力(一层半)准平衡(准无辐散)线性化海洋模型,即考虑一个上层为受风应力驱动的风生流层,下层为无穷深静止的情况;h为上层厚度的扰动;上、下层的密度则分别为ρ1,ρ2,且ρ1,ρ2均为常数;在此不考虑基流的影响,但考虑风场对大洋的强迫和瑞利摩擦的作用,并在有限矩形海域中进行求解和讨论.该海洋模型上层的控制方程组如下:

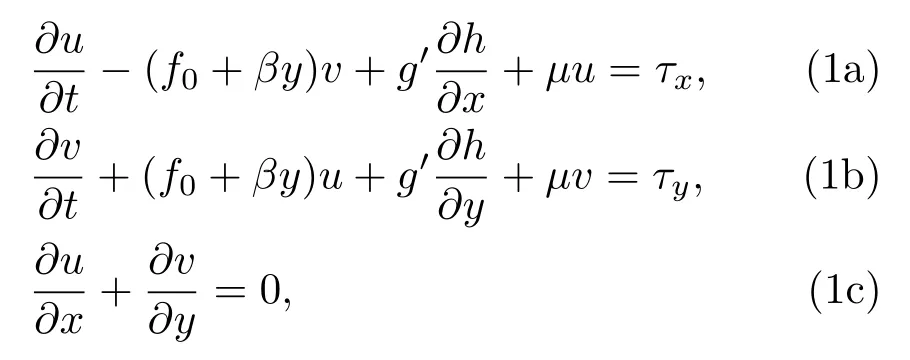
这里τx,τy为大气风应力的强迫,且设τx=γua,τy=γva,而ua,va为近海面风速,γ为比例系数,设为常数;µ为瑞利摩擦系数,也设为常数;f0为y0处的地转参数,β=∂f/∂y|y=y0,这里y0设为北半球中纬度β通道的中心位置;g′=g(ρ2−ρ1)/ρ1,为约化重力加速度.由该方程组的准无辐散性即(1c)式,可引入流函数ψ并有

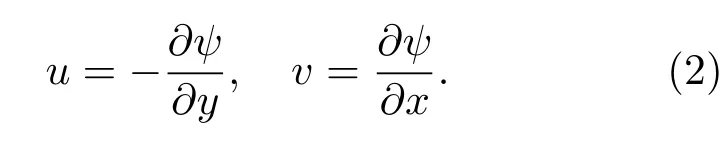
将(2)式代入(1)式,将(1c)式对y微商后再减去(1b)式对x的微商以消去h,可得

此处F=(∂τy/∂x−∂τx/∂y)=γζa,ζa=∂va/∂x−∂ua/∂y为近地面大气风场的旋度.

现求方程组(3)在该β通道中(中心线在y=y0处,半宽为M)并存在东、西边界(东、西海岸)时,此矩形大洋中的解析解,这样该方程组须满足以下边条件:

即在x=0,L处有刚壁(西、东海岸),在y=y0±M处(β通道的南、北边界)也设为刚壁.

因方程(3)是线性方程,故其解可写成自由波动的解和外强迫特解的叠加,这两个解分别用下标I,II来区分,即有

这里ψI满足自由波动方程,即方程(3)中取F≡0,同时满足边条件(4)式.ψI中因考虑了摩擦,又无外强迫和不稳定,故在一段时间后,其运动将因摩擦而趋于静止.ψII则满足方程(3),同时也满足边条件(4)式;这样(5)式中的解ψ最终由ψII即外强迫特解来决定.

3 外强迫特解的求取

为书写方便,以下略去ψII中的下标II.只考虑纬向风异常的强迫,并设该异常具有以下两种水平分布的振荡形式.第一种纬向风异常取为

注意到F=−γ∂ua/∂y,将(6a),(6b)式分别代入F的表达式,则以上第一、二种纬向风异常的强迫分别为

为解析求解方程(3)满足边界条件(4)式在外强迫(6a)或(6b)式下的特解,在(6a)式中设

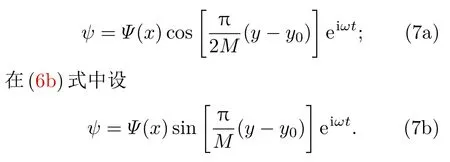
则(7a),(7b)式中的ψ显然满足边条件(4b)式.为方便,称(7a)式为第一种流场,(7b)式为第二种流场.将(6a),(7a)式或(6b),(7b)式代入(3)式后,可得

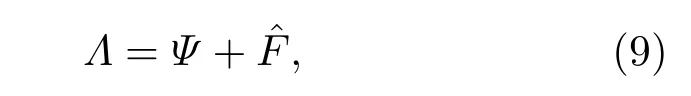
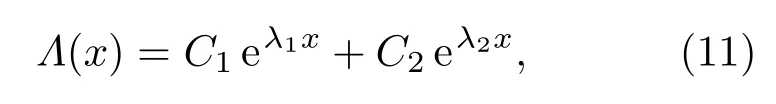
此处C1,C2为任意复常数,λ1,λ2中包含ω,µ,l,M等参数(但不包含L).于是有

现求(12)式中满足边界条件(4a)式的解.为此将x=0代入(12)式,有

将x=L代入(12)式,有

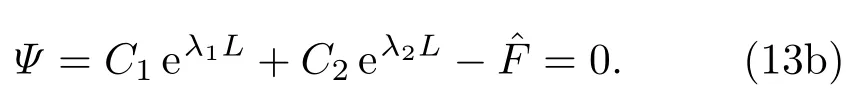
求解由(13a),(13b)式构成的关于C1,C2的二元一次方程组,可得为复数;

这样就求得了满足边界条件(4)式的解Ψ.将的表达式代入Ψ,并将Ψ代入(7a)和(7b)式.当取第一种纬向风异常即(6a)式时,有

当取第二种纬向风异常即(6b)式时则有

在ψ,u,v的解中,λ1,λ2中均含有ω.由(15),(16)和(6)式知,大洋流函数(流场)与外强迫纬向风二者的变化频率相同,均为ω.注意,外强迫纬向风振荡eiωt前的系数是实数,而大洋流函数(流场)对纬向风的响应(异常)eiωt前的系数是复数.这表明外强迫纬向风与大洋流函数(流场)响应之间有位相差,大洋的响应要滞后于纬向风的强迫.

以上ψ,u,v的解析解均用复函数表示,为得到有物理意义的实数解,将以上用复函数表示的解取实部即可.

4 大洋对纬向风强迫的响应

此有界大洋模型中大洋对大气纬向风异常强迫的响应即为上节中的外强迫特解.本节中,根据以上两种风场强迫,计算了相应的外强迫特解,并对此解做了分析讨论.这里取纬向风异常振幅取γ=10−9s−1,µ=5.7×10−12s−1,β=1.7536×10−11m−1s−1(40◦N处的值),有界海洋半宽M取1000 km,有界海洋长度L则取12000 km,该尺度与中纬北太平洋东西尺度相当.

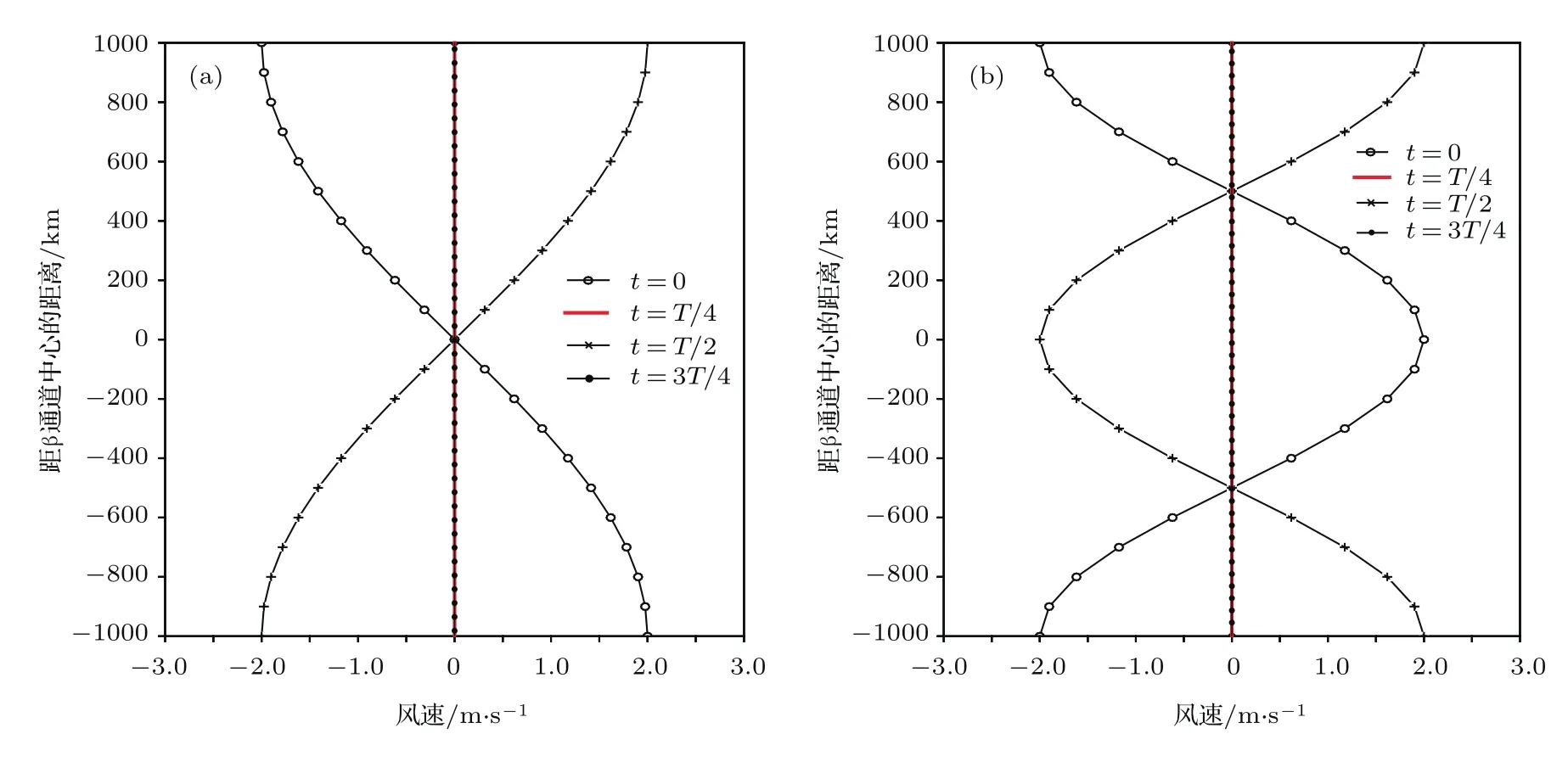
图1 外强迫风场在β通道中的分布 (a)第一种风场;(b)第二种风场Fig.1.Distribution of external forcing wind field in beta channel:(a)The first kinds of wind field;(b)the second kinds of wind field.

4.1 对第一种纬向风异常的响应

取强迫风场异常为第一种纬向风异常的形式,即取(6a)式,此时F为(6c)式,且有=由于北太平洋主要气候模态PDO具有准20年的年代际变化周期[2],为此这里取周期T=20 a,于是有ω=2π/T=9.9551×10−9s−1.此时纬向风异常ua在该β通道中的分布如图1(a)所示.在t=0时刻,在高纬有西风负异常,低纬有西风正异常,中纬异常不大;在t=T/4时刻,风场异常为0;在t=T/2时刻,风场异常与t=0时刻相反;在t=3T/4时刻,风场异常又为0;在t=T时刻,风场异常同t=0时刻.

图2 第一种风场强迫下大洋流函数的响应(单位为104m2/s)Fig.2.Response of oceanic flow function under the first kinds of forcing wind field(unit:104m2/s).

图2 和图3分别给出了在以上时刻第一种纬向风异常强迫下的大洋流函数和流场异常,即其响应.由图2和图3可见,该情况下海洋响应具有以下特点:在西海岸以东,大洋中有一个很强的长轴平行于西海岸的椭圆状流涡,在t=0和t=T/2时刻,分别呈气旋式和反气旋式旋转.在t=T/4和t=3T/4时刻,虽然纬向风异常为0,但是以上气旋式和反气旋式旋转的流涡仍未消失,这体现了流场响应对纬向风强迫的滞后性.西海岸以东有明显的海流西部强化现象.对于整个有界大洋,在t=0和t=T/2时刻,则分别有较弱的洋盆尺度的气旋性和反气旋性环流.此解较好地体现了PDO流场模的特征[22,23].这表明,第一种纬向风异常能够强迫出类似北太平洋PDO流场模的形态,不妨称该形态为PDO流场模的解析解.

图3 第一种风场强迫下大洋流场的响应(箭头单位为m/s) (a)t=0;(b)t=T/4;(c)t=T/2;(d)t=3T/4Fig.3.Response of oceanic flow field under the first kind of forcing wind field(arrow unit:m/s):(a)t=0;(b)t=T/4;(c)t=T/2;(d)t=3T/4.

4.2 对第二种纬向风异常的响应

取大气强迫风场异常为(6b)式,即取第二种纬向风异常强迫,此时F为(6d)式,且有=由于北太平洋次要气候模态NPGO有准13 a的年代际变化周期[24],为此取周期T=12 a,于是有ω=2π/T=1.6592×10−8s−1.此时纬向风异常ua在该β通道中的分布如图1(b)所示.在t=0时刻,高纬有西风负异常,中纬有西风正异常,低纬有西风负异常;在t=T/4时刻,风场异常为0;在t=T/2时刻,风场异常与t=0时刻相反;在t=3T/4时刻,风场异常又为0;在t=T时刻,风场异常同t=0时刻.

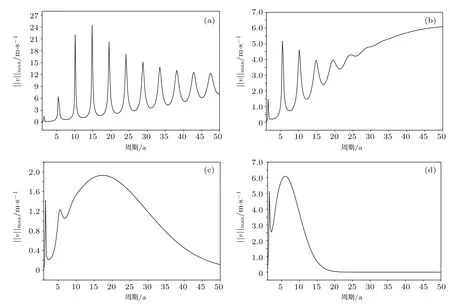
图4和图5分别给出了在以上时刻第二种纬向风异常强迫下的大洋流函数和流场异常,即其响应.由图4和图5可见,该情况下大洋响应具有以下特点:在西海岸以东,大洋中有一对很强的长轴平行于西海岸的椭圆状流涡.中高纬(y>y0)处的流涡在t=0和t=T/2时刻,分别呈气旋式和反气旋式旋转,中低纬(y

图4 第二种风场强迫下大洋流函数的响应(单位为104m2/s) (a)t=0;(b)t=T/4;(c)t=T/2;(d)t=3T/4Fig.4.Response of oceanic flow function under the second kinds of forcing wind field(unit:104m2/s):(a)t=0;(b)t=T/4;(c)t=T/2;(d)t=3T/4.

图5 第二种风场强迫下大洋流场的响应(箭头单位:m/s) (a)t=0;(b)t=T/4;(c)t=T/2;(d)t=3T/4Fig.5.Response of oceanic flow field under the second kinds of forcing wind field(arrow unit:m/s):(a)t=0;(b)t=T/4;(c)t=T/2;(d)t=3T/4.

最后,比较本节纬向风的分布可知,中纬度西风急流异常位置偏北,能强迫出PDO流场模的解析解,偏南则能强迫出NPGO流场模的解析解(图1).

5 有界大洋与外强迫风场的共振

共振是指一物理系统在特定频率下,比其他频率以更大的振幅做振动的情形,这些特定频率称之为共振频率.当阻尼很小时,共振频率大约与系统自然频率或称固有频率相等,后者是自由振荡时的频率.通常一个系统有多个共振频率,在这些共振频率上振动比较容易,而在其他频率上振动比较困难,且一般多重视系统中较低的共振频率.若引起振动的频率较宽,则该系统一般会“挑出”共振频率且随此频率振动,而将其他频率过滤掉.

5.1 共振现象的出现

为考察本文有界大洋模型与外强迫风场的共振,这里仍取以上各参数,但改变外强迫风场的振荡频率ω,因周期T=2π/ω,故也可通过改变周期T来实现.由于本文关心的是气候问题,故这里周期T的时段取0.25—50 a.若取第一种形式的风场强迫,考察大洋经向流v响应的最大值,则该最大值出现在y=y0处,由(15c)式知此处有

式中l=2.若取第二种形式的风场强迫,则该经向流v响应的最大值出现在y=y0+M/2处,由(16c)式知在此处仍有(17)式,只不过l=1.现对(17)式取模,则有

虽然以上两种风场强迫大洋经向流响应的模可用(18)式来表示,但因λ1,λ2中都包含参数ω,µ,l,M等,故对这两种风场强迫形式而言,该模值要分别计算.由(18)式可见,该模值为x的函数.现对某周期求有界大洋东西长度范围内(即x上)该模的最大值∥v∥max,再对0.25—50 a的外强迫振荡周期以0.25 a的间隔进行扫描,则该最大值随各年振荡周期的变化就表现为一条曲线,该曲线能反映大洋流场对外强迫风场振荡周期的响应情况.

取第一种风场强迫,仍取以上各参数(此时取µ=5.7×10−12s−1),图6(a)给出了∥v∥max对外强迫周期的响应曲线.由图6(a)可见,该曲线有3个峰,分别出现在0.75,4.75和22.25 a处(表1),其相应的峰值分别为1.47,1.74和2.56 m/s,其中22.25 a的峰高而宽,而前两个峰则较低较尖.此外,在周期约10 a处该曲线还有一个拐点,但未形成峰.以上情况表明,在取第4节的参数下,大洋对第一种风场强迫有3个明显的响应周期,分别为0.75,4.75和22.25 a,而最后者与PDO的年代际变化周期约20 a相近.这样对该处约20 a的PDO周期可做这样的解释:第一种纬向风强迫其可有各种长短不一的周期,因22.25 a的周期峰最宽阔,峰值也最高,故大洋流场对纬向风强迫的这个周期就能做出最突出的响应,并使该外强迫周期得到最强体现.以上情况表明,大洋会与纬向风强迫产生共振现象,前两个峰也是共振的结果,只不过没有最后一个峰的共振强.在用实际资料对冬季北太平洋做大气风场和大洋流场的联合复EOF分析[23]以及大洋流场的复EOF分析[22]中发现,两者第一模态的年代际变化主周期都为准20 a,且表现都十分明显;这表明实际情况中大气风场与大洋流场均有准20 a的周期(PDO的周期)存在,且大洋流场对大气风场的强迫有十分明显的响应,产生了共振,而该共振观点能对PDO的这种年代际变化给出合理解释.

取第二种纬向风强迫,其他参数均同图6(a)(此时仍取µ=5.7×10−12s−1), 图6(b)给出了相应的响应曲线.由图6(b)可见,该曲线总体分布态势与图6(a)相似,也有3个峰,分别出现在1.50,5.25和22.25 a处 (表2),其相应的峰值分别为2.81,3.36和5.11 m/s,均比图6(a)中大,这是由于取同样的纬向风振幅˜ua时,图6(b)中的强迫要较图6(a)中的大的缘故(请比较(6c),(6d)式中˜F表达式的不同).22.25 a的峰同样较高较宽阔,而前两个峰也均较低较尖,此外在周期约10 a处该曲线也有一个拐点,但也未形成峰.以上情况表明,大洋对第二种纬向风强迫也有三个明显的响应周期,分别为上述的1.50,5.25,22.25 a,且最后者与图6(a)中的周期相同.因22.25 a的周期峰最宽阔,峰值最高,故大洋流场也能对第二种纬向风强迫做出最大响应,并使其得到最强体现.这里,大洋的共振现象也很明显.在对冬季北太平洋做大气风场和大洋流场的联合复EOF分析[23]以及大洋流场的复EOF分析中[22],发现二者第二模态的年代际变化主周期都为准18 a,且表现也都十分明显,这表明实际情况中大气风场与大洋流场都有准18 a的周期存在,该准18 a的主周期也与图6(b)中峰值最高的22.25 a的周期数值相差不大.此外,NPGO有13 a的年代际变化周期[24],该周期相应于图6(b)中曲线拐点处的周期.

图6 ∥v∥max值的曲线(µ=5.7×10−12s−1) (a)第一种流场;(b)第二种流场Fig.6.Curve of value ∥v∥max(µ =5.7 × 10−12s−1):(a)The first kinds of flow field;(b)the second kinds of flow field.

在此还注意到,λ1,λ2中均不包含参数故纬向风强迫的大小不会改变上述响应曲线的分布形态(含曲线上峰出现的周期),这表明大洋共振现象的周期与纬向风强迫的大小无关,而∥v∥max则与γ˜ua成正比.

5.2 有界大洋自由振荡的固有周期

上面已指出固有频率在共振中的作用,而且一般多重视系统中较低的固有频率.因频率ω与周期T有关系,T=2π/ω,故求固有频率等价于求固有周期,而此时较低的固有频率则有较长的固有周期,即年代际变化.以下求固有频率和固有周期.

考虑无摩擦的有界大洋自由振荡解ψI,略去下标I后其控制方程组仍为(3)式,只不过此时有µ=0,F=0,而边条件仍为(4a)式和(4b)式.设波解(7a)或(7b)式后有(8)式,只不过现在该式中取µ=0和˜F=0.因˜F为0,故Λ=Ψ,并满足方程(10),求解该方程有

此处,λ1,λ2和C1,C2的意义与第3节相同.(19)式要满足边条件(4a)式,则应有C1=−C2和C1(eλ1L−eλ2L)=0;要使C1(eλ1L−eλ2L)=0,就必须有 eλ1L−eλ2L=0,取模则有

(20)式表明,要使有界大洋自由振荡有非零解,其自由振荡的频率不能任意,必须满足(20)式(因λ1,λ2中含有该振荡的频率),该频率即为此有界大洋自由振荡的固有频率,相应的周期为固有周期.注意到(7a)式或(7b)式后可知,对第一种流动,自由振荡的解为

在(21a)式和(21b)式中,任意复常数C1为有界大洋自由振荡的复振幅;ω为其固有频率,须满足(20)式. 当µ= 0(无阻尼)时,注意到∥eλ1L−eλ2L∥即为(18)式第二个×号后表达式的分母,此时二者的λ1,λ2值也相同,故有界大洋自由振荡的固有周期也就是该大洋对外强迫风场响应的共振周期,这也与共振的概念相一致;此时在共振周期上,该大洋响应为无穷大,因其分母为0.

为考察固有周期,在λ1,λ2中取µ=0,其他参数同第4节,并采用0.25 a的时间间隔,在0.25—50 a的时段上,对∥eλ1L−eλ2L∥进行扫描,以便得到∥eλ1L−eλ2L∥的曲线.图7(a)和图7(b)分别给出了第一、二种流场的曲线图.由图7(a)可见,在0.25—50 a的时段上,曲线有11个值小于0.2的尖点.这些尖点对应的周期即为固有周期,且这些尖点的值本应为0,但因这里是按0.25 a间距扫描的以及误差等的影响,故其值尚未达到0.图7(b)的情况与图7(a)类似.表1则给出了扫描得到的第一、二种流场的固有周期数值.

图7 ∥eλ1L− eλ2L∥值的曲线 (a)第一种流场;(b)第二种流场Fig.7.Curve of value ∥eλ1L − eλ2L∥:(a)The first kinds of flow field;(b)the second kinds of flow field.

表1 第一、二种流场的固有周期(单位:a)Table 1.Natural cycles of the first and second kinds of flow field(unit:a).

5.3 摩擦对共振的影响

仍取以上各参数和两种风场,但改变摩擦系数µ,来考察摩擦大小对共振现象的影响.现取µ值(单位为10−10s−1)分别为0.001,0.01,0.057,0.1,1,计算了以上两种纬向风强迫的响应.图8和图9分别给出了取第一、二种纬向风强迫的大洋响应曲线,取µ=0.057×10−10s−1的曲线则见图6,表2和表3分别给出了各响应曲线上与峰值相对应的周期,即共振周期.

图8 第一种风场强迫下∥v∥max值的曲线 (a)µ =0.001×10−10s−1;(b)µ =0.01× 10−10s−1;(c)µ =0.1×10−10s−1;(d)µ =1×10−10s−1Fig.8.Curve of∥v∥maxvalue under the first kind of forcing wind field:(a)µ =0.001× 10−10s−1;(b)µ =0.01×10−10s−1;(c)µ =0.1×10−10s−1;(d)µ =1×10−10s−1.

表2 不同µ时第一种纬向风强迫下大洋响应的共振周期(单位:a)Table 2.Resonance period of oceanic flow field under the first kind of forcing zonal wind at dif f erent values ofµ(unit:a).

图9 第二种风场强迫下∥v∥max值曲线 (a)µ=0.001;(b)µ=0.01;(c)µ=0.1;(d)µ=1(单位均为10−10s−1)Fig.9.The curve of value ∥v∥maxunder the second kinds of forcing wind field:(a)µ =0.001;(b)µ =0.01;(c)µ =0.1;(d)µ =1(units ofµ:10−10s−1).

表3 不同µ时第二种纬向风强迫下大洋响应的共振周期(单位:a)Table 3.Resonance period of oceanic flow field under the second kinds of forcing zonal wind at dif f erent values ofµ(unit:a).

由图6、图8、图9和表2、表3可见,有界海洋对纬向风强迫响应的极大值呈离散分布状态,即其出现在某些离散的特定周期上;当摩擦很小时,响应十分强烈,这表明有剧烈的共振发生,此时外强迫的共振周期与该有界海洋本身的固有周期应相同(表2和表3与表1比较),而该固有周期应与有界大洋本身的特点有关而不依赖于外强迫(见5.2节及以下的5.4节).由图6、图8、图9和表2、表3还可见,在0.25—50 a的周期内,当µ=0.001×10−10s−1时该共振周期都约为:1,5,10,14,19,24,29,33,38,43,48 a,其间隔约5 a.随着摩擦的增大,该共振的阻尼增加,响应减弱,共振周期的个数也在减少.当取µ=0.057×10−10s−1时,其与实际北太平洋的情况较为一致.摩擦再加大,则其最长的周期尺度变短,峰形也变尖.

5.4 有界大洋尺寸对共振的影响

改变有界大洋的东西长度L值和半宽M值,来考察其对共振周期的影响. 在第一、二种纬向风强迫下,取以上各参数并取摩擦µ=0.001×10−10s−1和0.057×10−10s−1,分别计算L=12000,10000,8000,6000 km时有界海洋的共振周期,此时其半宽M都取1000 km.因两种风场强迫的结果十分接近,故取整数年后在一张表中列出.由表4(取µ=0.001×10−10s−1的结果)可见,该L值的确对共振周期有明显影响,随着L值的减小,相邻两个共振周期的间隔增大,而共振周期个数则由11个减至6个.当取µ=0.057×10−10s−1时,对应各L都只有3个共振周期出现,前两个共振周期分别为1和5 a,最后一个周期则随L由大至小分别为22,25,27,31 a,并也有L值对共振周期影响明显的特点.

再改变有界海洋的半宽M值来考察其影响.同样取以上各参数并取摩擦µ=0.001×10−10s−1和0.057×10−10s−1,分别计算有界海洋相对于其半宽M=1000,900,800,700,600,500 km时的共振周期,此时L值取12000 km.计算结果表明,对所取的两种摩擦,在以上M的取值范围,共振周期及个数不随半宽M值改变,当取µ=0.001×10−10s−1时,其等于表4中的第二行.当取0.057×10−10s−1时,其为1,5,22 a. 这表明,有界海洋东西方向的长度L对共振周期值起着决定作用,而其半宽M则影响甚微.

表4 取µ=0.001×10−10s−1而L不同时大洋对风场强迫响应的共振周期(单位:a)Table 4.Resonance period of oceanic flow field under the forcing wind field at dif f erent values of L whenµ =0.001×10−10s−1(unit:a).

5.5 讨 论

以上结果表明,一旦纬向风强迫的周期与该有界海洋固有周期相同或相近,则有界大洋就会与其发生共振,使响应振幅急剧增大,即此时有界大洋会做出强烈响应.若纬向风强迫的周期与此大洋的固有周期相差很远,则此大洋对其响应就不会太大(参见图6、图8和图9).这种情况说明本文的有界大洋系统会“挑出”共振频率且随此频率强烈振动,而将其他频率过滤掉,亦即该固有周期对外强迫周期具有挑选功能,从而也就锁定了PDO和NPGO年代际变化的周期.虽然本文仅考虑了纬向风强迫作用,但是得到的年代际振荡周期却与实际情况相同或接近,这也表明实际中该共振作用是存在的.

从用实际资料所做的对大气风场和大洋流场的联合复EOF分析来看,大气风场的确有年代际变化[23].最近本课题组采用实际资料对亚洲夏季风建立期间的全球热带大气风场异常做了复EOF分析,发现其第一模态有非常显著的19 a年代际变化,第二模态有明显的21 a和13 a的年代际变化;因该复EOF分析仅使用大气实际资料,这就进一步证实了实际大气风场确有年代际变化的存在.此外,近年来对季风年代际变化的研究工作也不少[26],这从另一侧面反映了大气风场年代际变化存在的客观事实.而这种年代际变化的风场会强迫大洋对其做出响应.当强迫大洋的大气风场频率(周期)与该大洋的固有频率(固有周期)相近或相同时,则有共振发生.

对大气风场存在年代际变化的原因可用大气中各种随机波动的非线性相互作用来解释,该相互作用能产生从高频到极低频的各种波动,如将频率分别为ω1和ω2的两个波动相乘时,就会产生频率为ω1−ω2和ω1+ω2的波动,从而在大气中产生广谱的随机波动,即大气白噪声,其中也包含了极低频(年代际变化)的随机波动,即大气红噪声;同样,大气与海洋,大气与陆面等的非线性相互作用也会产生大气白噪声,证明大气中白噪声是普遍存在的.当大气白噪声(广谱的随机波动)风场强迫有界大洋流场时,因上述共振作用,该大洋就会“挑出”其各个共振频率,并随之做出强烈响应,而对其他频率则响应不大,也即海洋流场对大气白噪声风场强迫的响应都是单色的.对于白噪声中包含的红噪声,海洋对其的响应都是某些深浅不一的单色红.将以上观点用于PDO,能更好地解释PDO的随机强迫理论,即白噪声的风场可以强迫出红噪声的海洋异常;不过在此用红噪声比喻不够确切,应用某种单色红,因PDO的周期(频率)是确定而非随机的.

由以上情况知,共振的作用非常重要,因其起到了从白噪声中挑选各种单色的作用,若挑选的各种单色有些落在红色范围,海洋就会出现PDO,NPGO等年代际变化.还要强调的是,风场的强迫同样也很重要.若无风场强迫,即使其存在年代际变化,对有界大洋无摩擦的自由振荡流场,也不会形成PDO或NPGO的流场模,即(21a)式和(21b)式的流函数(图略)会分别与图2和图4有明显不同;当考虑到摩擦后,该流场最终呈静止状态;故该风场对大洋流场的强迫作用是不可忽略的.

本文的海洋模型是线性的,这与Sverdrup,Stommal,Munk等经典工作类似,结果也都大致符合实际,本文也是如此,这表明线性模型是可接受的.然而本文并不排斥大气与大气之间、大洋与大洋之间、大气与大洋之间的非线性相互作用;不但如此,还认为这种非线性相互作用对大洋年代际变化如PDO,NPGO等是十分重要的.正如上面所述,该非线性相互作用是大气白噪声风场的来源,如无该白噪声风场,就不会有大气白噪声风场对海洋流场的强迫,也不能从共振中挑选出某些单色红的海洋流场异常,也就不会产生PDO和NPGO.综上,非线性作用、大气风场强迫和共振是造成PDO和NPGO的三个关键因子,三者缺一不可.

本文主要是对后两个因子做了阐述.对第一个因子,因非线性相互作用的复杂性,本文并未涉及,只是默认其结果可形成大气白噪声风场.当然以上说法是对PDO随机强迫理论而言的,也有从统计出发的观点认为[27],太阳活动可引起PDO现象.对此本文也能这样解释:太阳活动通过影响阿留申低压活动使得大气风场产生了与海洋年代际固有周期相近或相同的周期变化(两者均约为22 a),该大气风场对海洋流场施加强迫,从而形成PDO.后两个因子仍起着重要作用,而第一个因子则换成了太阳活动的强迫.

关于共振波动的性质,因本文采用了准平衡(准无幅散)近似,故仅包含Rossby波.Sverdrup解可看作Rossby波方程的定常特解,且该解结构由风场决定,从该解相当于共振Rossby定常波这一点来看,本文的解亦为共振Rossby波,只不过是时变而非定常的;另外,本文还具体揭示了共振的情况和机制.

6 结 语

本文采用中纬β通道中约化重力准平衡线性海洋模型,对有界大洋解析求解了纬向风强迫下其流场的响应,讨论了该响应中的共振问题,对引言中所提的问题做了肯定的回答.

1)在本文所取的参数及纬向风场强迫下,有界大洋的响应分别类似于先前诊断所得的冬季北太平洋PDO和NPGO的流场模,可称之为这两个流场模的解析解.

2)该PDO和NPGO流场模的解析解分别表现为:在大洋西海岸以东,前者有一个椭圆状流涡,后者则有南北两个旋转方向相反的流涡并构成流涡偶;在整个大洋,前者有一个洋盆尺度环流,而后者大洋南北分别有两个旋转方向相反的洋盆尺度环流.

3)中纬度西风急流异常位置偏北和偏南,分别能强迫出PDO和NPGO流场模的解析解;流函数(流场)响应的强度与纬向风强迫大小成正比,而响应频率(周期)则与纬向风强迫频率(周期)相同,但大洋响应要滞后于纬向风的强迫.

4)当纬向风强迫频率(周期)与该大洋固有频率(周期)相同时,二者会有共振发生,此时大洋响应最强烈,而二者频率(周期)相差较远时,该响应则不大;摩擦越小该共振就越强,共振的个数也越多;该解析解的性质为时变的共振Rossby波.

5)有界大洋东西向的长度对其固有频率(周期)即共振频率(周期)有明显影响并起着决定作用,当长度减小时,相邻两个共振周期的间隔会增大.

6)非线性相互作用使随机风场具有各种频率;通过该共振,可从中选出某些固有频率,在该频率上流场对风场响应最强烈,从而也就锁定了PDO和NPGO的周期;非线性相互作用、风场对流场强迫、共振是造成PDO和NPGO的3个关键因子.

最后要说明的是,因本文是解析研究,对模型做了必要简化(如取东、西海岸线是南北走向的,仅采用纬向风的强迫等),这与实际北太平洋的情况不完全相同,虽然本文结果总体与实况一致,但也有些差异,这是正常和可以理解的.

[1]Mantua N J,Hare S R,Zhang Y,Wallace J M,Francis R C 1997Bull.Amer.Meteor.Soc.78 1069

[2]Newman M,Alexander M A,Ault T R,et al.2016J.Climate29 4399

[3]Yang X Q,Zhu Y M,Xie Q,Ren X J,Xu G Y 2004Chin.J.Atmos.Sci.28 979(in Chinese)[杨修群,朱益民,谢倩,任雪娟,徐桂玉2004大气科学28 979]

[4]Wu D X,Lin X P,Wan X Q,Lan J 2006Acta Oceanol.Sin.28 1(in Chinese)[吴德星,林霄沛,万修全,兰健2006海洋学报28 1]

[5]Sun D,Bryan F 2010Climate Dynamics:Why does Climate Vary?(Washington DC:American Geophys Uninon Press)p123

[6]Liu 2010Deep-Sea Res.II57 1098

[7]Wang S S,Guan Y P,Li Z J,Cao Y,Huang J P 2012Acta Phys.Sin.61 169201(in Chinese)[王闪闪,管玉平,Li Zhi-Jin,Cao Yi,黄建平2012物理学报61 169201]

[8]Liu Q Y,Li C,Hu R J 2010Climatic Environ.Res.15 217(in Chinese)[刘秦玉,李春,胡瑞金 2010气候与环境研究15 217]

[9]Lorenzo E D,Schneider N,Cobb K M,Franks P,Chhak K,Miller A,Mcwilliams J,Bograd S,Arango H,Curchitser E 2008Geophys.Res.Lett.35 L08607

[10]Cummins P F,Lagerloef G S E,Mitchum G 2005Geophys.Res.Lett.32 L17607

[11]Furtado J C,Lorenzo E D,Schneider N,Bond N A 2011J.Climate24 3049

[12]Zhang W,Luo M 2016Atmos.Sci.Lett.17 437

[13]Rafter P A,Sanchez S C,Ferguson J,Carriquiry J D,Druf f el E R M 2017Quaternary Sci.Rev.160 108

[14]Chhak K,Lorenzo E D 2009J.Climate22 1255

[15]Ceballos L,Lorenzo E D,Hoyos C D 2009J.Climate22 5163

[16]Cabanes C,Huck T,Verderee C D 2006J.Phys.Oceanogr.36 1739

[17]Qiu B,Chen S M 2010Deep-Sea Res.II.57 1098

[18]Zhang Y C,Zhang L F 2009Adv.Earth Sci.24 1119(in Chinese)[张永垂,张立凤2009地球科学进展24 1119]

[19]Zhang Y C,Zhang L F,Luo Y 2010J.Trop.Meteor.16 51

[20]Zhang Y C,Zhang L F,Lyu Q P 2011Adv.Atmos.Sci.28 158

[21]Lyu Q P,Zhang W F,Zhang M 2013Climatic Environ.Res.18 124(in Chinese)[吕庆平,张维锋,张铭 2013气候与环境研究18 124]

[22]Lyu Q P,Lu X,Zhu J,Dai W H,Zhang M 2015J.Marin.Sci.33 1(in Chinese)[吕庆平,卢姁,朱娟,戴文灝,张铭2015海洋学研究33 1]

[23]Zhang D L,Lyu Q P,Zhang L F 2015Chin.J.Atmos.Sci.39 692(in Chinese)[张东凌,吕庆平,张立凤2015大气科学39 692]

[24]Lyu Q P,Lu K C,Zhang M 2013Climatic Environ.Res.18 210(in Chinese)[吕庆平,路凯程,张铭2013气候与环境研究18 210]

[25]Lu K C,Yu J,Lyu Q P,Zhang M 2014Adv.Marin.Sci.32 467(in Chinese)[路凯程,于杰,吕庆平,张铭 2014海洋科学进展32 467]

[26]Ding Y H,Sun Y,Liu Y Y,Si D,Wang Z Y,Zhu Y X,Liu Y J,Song Y F,Zhang J 2013Chin.J.Atmos.Sci.37 253(in Chinese)[丁一汇,孙颖,刘芸芸,司东,王遵娅,朱玉祥,柳艳菊,宋亚芳,张锦2013大气科学37 253]

[27]Qu W Z,Huang F,Zhao J P,Jia Y L,Li C,Yue S H 2008Oceanol.Limnol.Sin.39 552(in Chinese)[曲维政,黄菲,赵进平,加英莱,李春,岳淑红 2008海洋与湖沼 39 552]