部分浸没圆柱壳声固耦合计算的半解析法研究∗
郭文杰1)3) 李天匀1)2)3) 朱翔1)2)3) 屈凯旸4)
1)(华中科技大学船舶与海洋工程学院,武汉 430074)
2)(高新船舶与深海开发装备协同创新中心,上海 200240)
3)(船舶与海洋水动力湖北省重点实验室,武汉 430074)
4)(上海交通大学船舶海洋与建筑工程学院,上海 200240)
(2017年12月18日收到;2018年2月7日收到修改稿)
1 引 言
圆柱壳结构以其优异的几何特性、力学特性被广泛应用于土木、化工、航空航天、海洋工程等诸多领域,比如输油管道、储液罐、潜艇耐压壳等.20世纪,国内外针对圆柱壳-流场耦合系统声振问题已有大量的文献报道[1−4],也形成了较为完善的理论体系,在这些工作中,大多数的研究均针对比如全充液或者全浸没问题(无限流域)这种壳体与流场完全耦合的振动、声学问题的研究.但是对于实际的工程问题,流域往往是存在边界的,尤其是当结构靠近流体边界时,或者结构内带有自由液面时,如果忽略流体边界的影响,计算结果往往是有偏差的[5].
自由液面作为一类典型的边界条件,其与圆柱壳结构的耦合动力学特性吸引了许多学者对其开展研究.Huang[6]基于镜像原理研究了平面波入射下二维圆柱壳的散射声场,Hasheminejad和Azarpeyvand[7]进一步将该方法延展到研究平面波入射下1/4空间二维圆柱的声散射问题.白振国等[8]采用镜像原理建立了有限水深环境中二维圆柱壳的振动声学物理模型,并探讨了潜深对声场分布和衰减特性的影响规律.郭文杰等[9,10]基于镜像原理和Graf加法定理建立了有限水深下有限长圆柱壳-流体耦合振动的解析模型,并基于傅里叶变换及稳相法提出了该系统远场声压的快速准确预报方法.
上述研究主要针对壳体结构完全浸没在水中的情况,这一类问题中,结构完全与流场耦合,其声振耦合方程的描述相对容易.实际上,还有一类问题,就是结构与流场部分耦合的情况,比如系泊状态下的潜艇、舰船等.对于系泊状态下圆柱壳声固耦合分析的研究工作则相对较少,尤其是圆柱壳轴线平行于自由液面时的解析或半解析研究更是鲜有报道,这是因为系泊状态下流体载荷解析表达式和耦合方程更难以得到.为了解决壳体部分充液的振动问题,Amabili[11]给出了两种近似的方法,一种是用以圆柱圆心为原点构成的扇形边界近似替代自由液面的方法,但是这种方法仅适用于浸没角度较小的情况;另一种是用部分环状区域代替原始边界,但这种方法也仅适用于浸没角度小于π的工况.值得注意的是,Amabili提出的第一类方法是可以推广到壳体部分浸没问题中[12],并明确指出浸没角度的适用范围仅为−π/8—π/8;但是第二类方法无法推广到外流场.基于Amabili提出的自由液面近似处理方法,Ye等[13]研究了系泊状态下无限长圆柱壳声振特性.
此外,其他一些学者也研究过部分浸没或者部分充液的壳体耦合振动问题,Selmane和Lakis[14]将圆柱壳沿周向分割成微段,再结合波动法研究了部分充液时其流固耦合特性.Ergin和Temarel[15]基于瑞利-李兹法研究了部分充液或者部分浸没时圆柱壳固有频率.Krishna和Ganesan[16]基于多项式级数及有限元法计算了部分充液圆柱壳固有频率以及附连水质量.但是这些研究工作实际上仅仅考虑了湿表面流体的影响而并未考虑自由液面边界条件的声学效应,尚无法揭示自由液面对声振特性的影响.另外还有一些学者通过实验的手段分析了部分充液的圆管自振特性[17]或者附连水质量效应[18],但依然无法从机理上求解这类问题.
需要强调的是,在壳体与流场部分耦合的问题中,半充液或者半浸没情况是个特例,因为这种模型下自由液面刚好在壳体横截面的水平坐标轴上,容易得到流体载荷的解析表达式,可采用正弦三角级数[19]来自动满足自由液面的边界条件.基于这类解析表达式,Li等[20]对半浸状态下全充液圆柱壳的声辐射特性进行分析,李天匀等[21]针对有限长半充液圆柱壳的自由振动及受迫振动特性开展研究.尽管本文工作是要解决部分浸没这类更为普遍的工况,而文献[19—21]中的研究工作仅能解决半浸没这种特殊工况.但是,文献[19—21]中关于在半浸没情况下通过采用正弦三角级数来自动满足自由液面下的声压释放条件的思路却可以借鉴到本文的研究工作中来.
针对更一般的壳体与流场部分耦合,如部分浸没等问题,此时自由液面与圆柱壳的圆心不共面.这给问题的描述和求解带来了很大的挑战.为解决这个问题,本文将声压函数和壳体位移函数建立在不同的坐标系下.具体来讲,将声场坐标系的原点建立在自由液面上,并采用正弦三角级数来满足自由液面上的声压释放边界条件;将壳体运动方程建立在以圆柱圆心为坐标原点的坐标系下.由此,便可以分别得到声压函数与壳体位移函数在各自坐标系下的解析表达式,为解析求解部分浸没问题奠定了基础.然后,再利用Galerkin法处理结构与声场部分声固耦合的界面上的速度连续条件,并通过两坐标间的几何关系求得声压幅值与壳体位移幅值之间的关系矩阵,最终便可以求解该声固耦合系统方程.本文方法的提出可以便捷有效地解决系泊状态下圆柱壳的声振问题,丰富了该问题理论研究的内涵,也为解析求解浮态问题提供了新的思路.
2 理论分析
2.1 物理模型
为了便于研究,本文假设圆柱壳轴向是无限长的,且激励力沿轴向是均匀分布的,由此本文的数学物理模型是一个典型的平面应变模型(即二维模型).二维圆柱壳厚度为h,中面半径为Rs,杨氏模量为E,泊松比为µ;密度为ρs,部分浸没于密度为ρf;声速为cf的流体中,壳体轴系与自由液面平行.如图1所示,以壳体圆心O为坐标原点的极坐标系(r,φ)为结构坐标系,φ的取值范围为0—2π,以壳体圆心正上方与自由液面的交点Q为原点的极坐标系(R,θ)为声场坐标系,θ的取值范围为0—π,
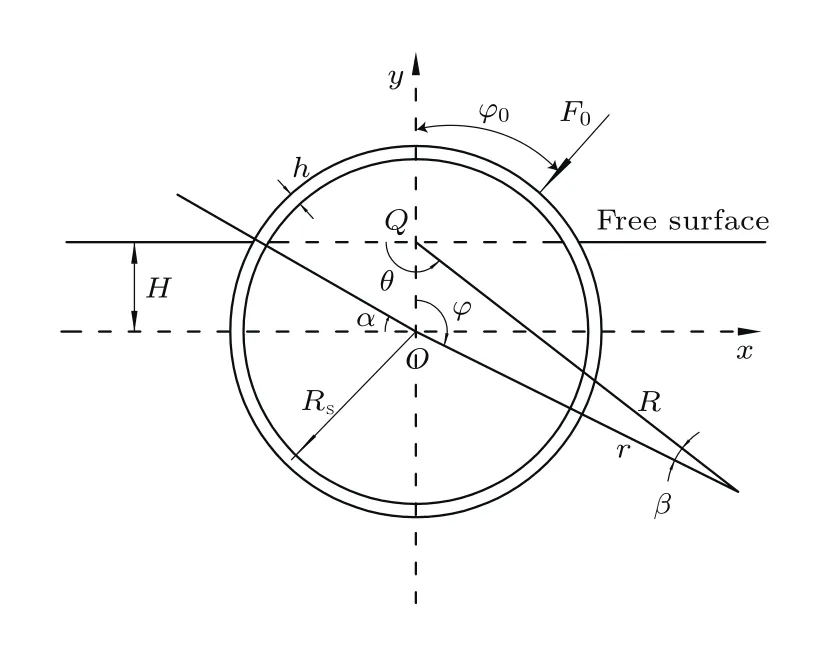
图1 物理模型坐标图Fig.1.Coordinate figure of the physical model.
定义Q点到O点距离为浸没深度H,浸没角度α满足sinα=H/Rs,当自由液面在壳体圆心下方时,H取值为负值.两类坐标系与平面上任一点的夹角定义为β.当自由液面在壳体圆心上方时β取值为正值,在下方时β取值为负值.径向激励力幅值为F0,激励角度为φ0.
2.2 声学边界条件
本文的物理模型是典型的声固耦合模型,而这项研究工作的难点和重点之一就是得到满足所有对应的声学边界条件的声压解析表达式.
首先,声压p必须满足声学Helmholtz方程:
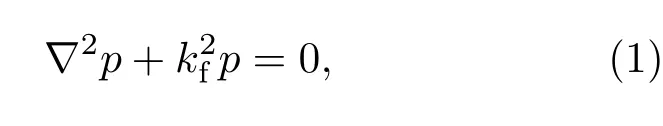
其中kf=ω/cf为声波波数,ω=2πf为角频率,f表示频率,∇2表示拉普拉斯算子.
其次,声压表达式还要满足无限远处Sommerfeld辐射条件:
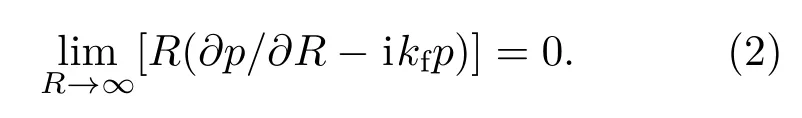
最后,自由液面处的声压需满足声压释放条件(因为研究的频率相对较高,自由表面的重力波可以忽略不计;此外由于自由液面以上空气密度远小于水,故作为真空处理)

实际上,当声场坐标系原点建立在自由液面上时,可以通过采用正弦三角级数来自动满足自由液面声压为零的边界条件[19],具体形式为
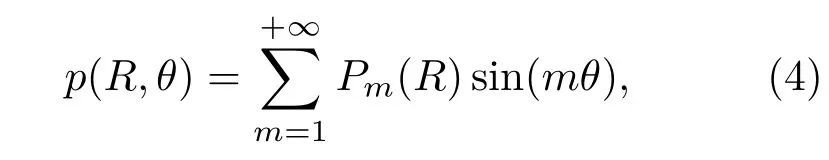
其中m为正弦三角级数的序数,Pm(R)为对应的声压幅值函数.
对于自由液面上的任意点,角度θ=0或π,将其代入(4)式,可以得到自由液面声压的表达式:
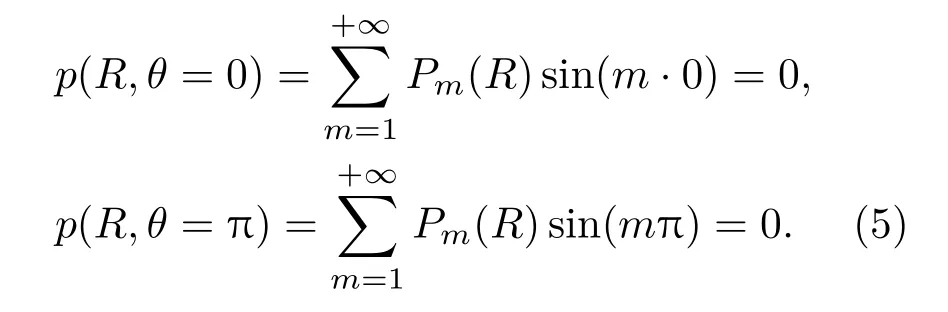
显然此类正弦三角级数可以用来满足自由液面声压释放条件,此外采用三角函数也更有利于应用分离变量法来求解Helmholtz方程.由此可以得到声压幅值函数Pm(R)的解析表达式:
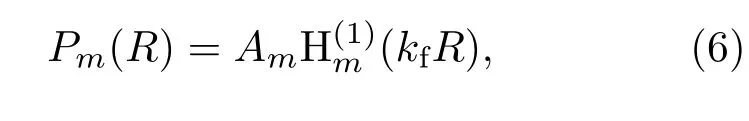
其中H(1)m()为第m阶第一类汉克尔函数,Am为声压幅值.
由于第一类汉克尔函数在远场自动满足Sommerfeld辐射条件,因此将(6)式代入(4)式可以得到满足以上声学边界条件的声压解析表达式:
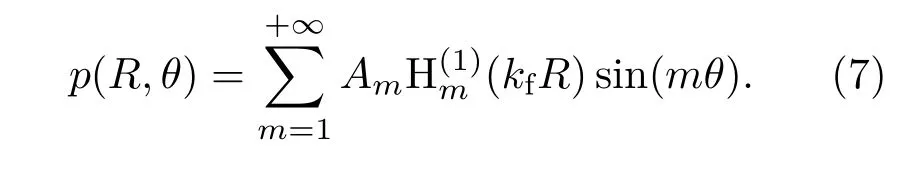
2.3 壳体运动方程
得到声压的解析表达式后,接下来需要建立壳体运动方程.本节采用二维Flügge薄壳理论[22],具体的方程为(为简洁,后文略去简谐时间项exp(−iωt)):
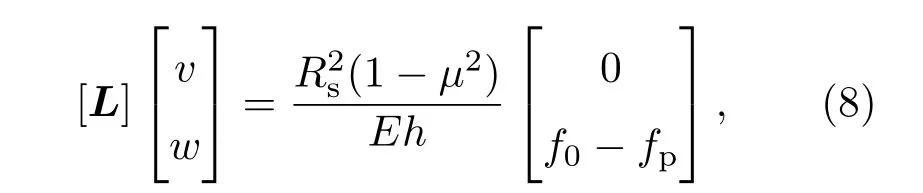
其中v和w分别是壳体中面切向和径向位移,fp表示作用在圆柱壳表面的声载荷,f0表示外激励力载荷,[L]是二维Flügge薄壳方程中的微分算子矩阵,具体如下:
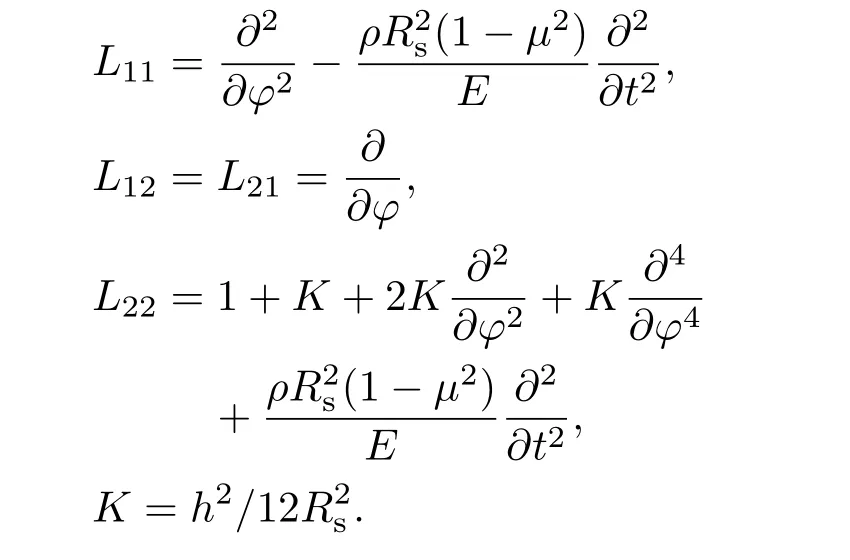
由于壳体和声介质是部分耦合,因此(8)式中fp应表示为分段函数的形式:

假设作用于圆柱壳的激励力是一个沿轴向均匀分布的无限长径向线力,激励力位于结构坐标系的(Rs,φ0)处,则激励力载荷可以表示为
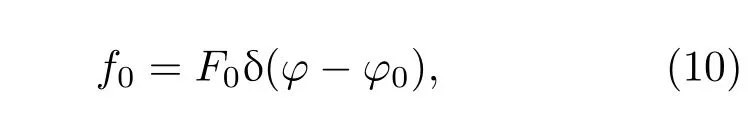
其中δ()表示狄利克雷函数.
对于圆柱壳结构,由于周向的周期性,其位移及载荷函数可以在周向展开为傅里叶级数的形式[8]:
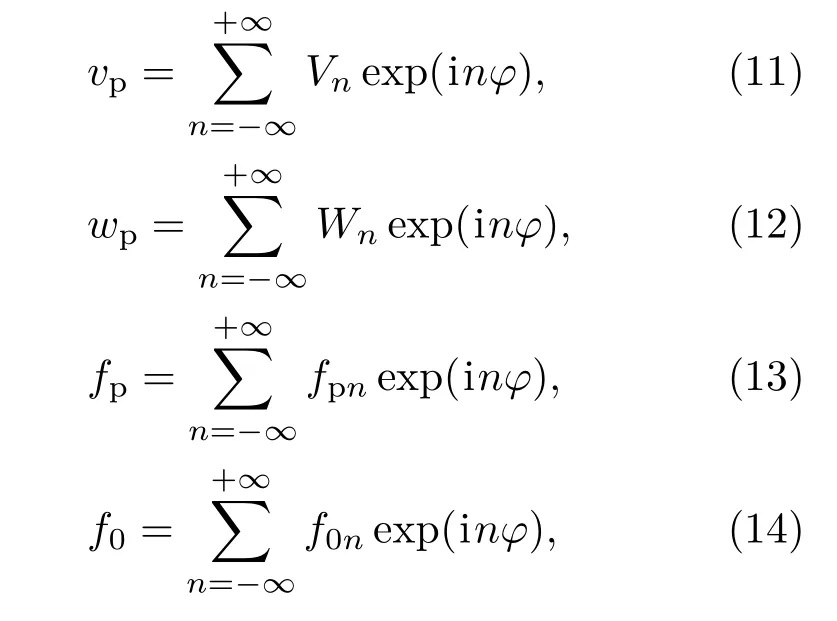
其中Vn和Wn分别是周向和径向位移幅值,fpn和f0n分别表示壳体表面声载荷fp以及激励力载荷f0的幅值,n是傅里叶周向展开序列数.
因为(9)和(13)式是壳体表面声载荷fp的不同形式的表达式,利用正交化处理,可得fpn的表达式:
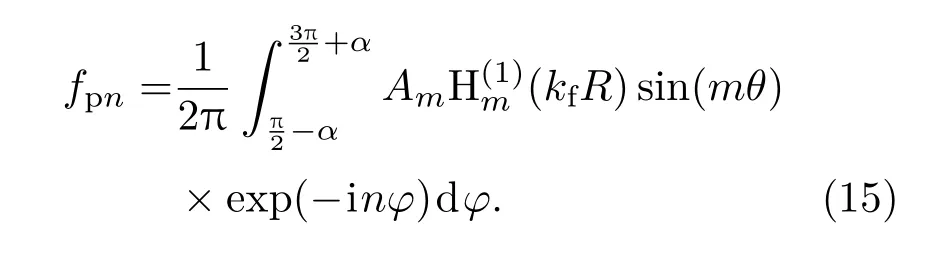
由图1可知,空间中任意点的结构坐标与声学坐标有如下关系:
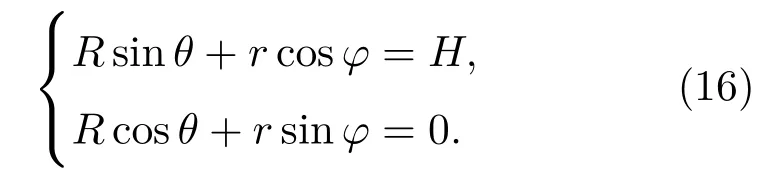
因此对于流固耦合面上任一点,令r=Rs,则(R,θ)在声学坐标系下的坐标可以由(16)式解出:
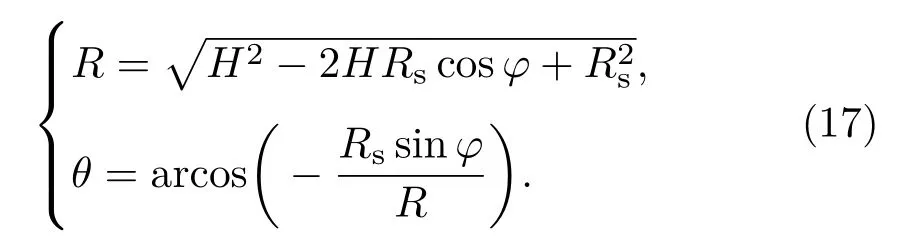
将(17)式代入(15)式即可对fnp进行求解,但是由于积分中包含汉克尔函数,无法直接进行积分计算,因此本文采用离散求和的形式来近似计算.首先将积分域均分为K段,然后取各段中点值代入求和公式中:
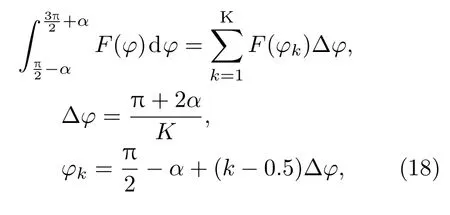
其中F(φ)表示需要进行积分的函数,通过大量算例表明K取100时收敛性已经很好.
同理,(10)和(14)式是外激励力f0的不同形式的表达式,利用正交化处理,可以得到f0n的表达式:
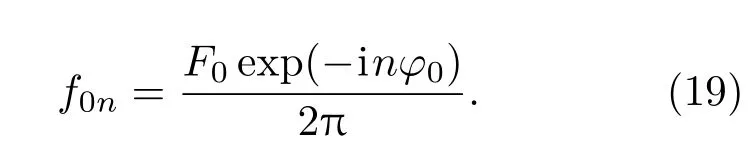
然后将(11)—(14)式代入到(8)式中,并进行正交化处理,可以得到解耦后的壳体运动方程:
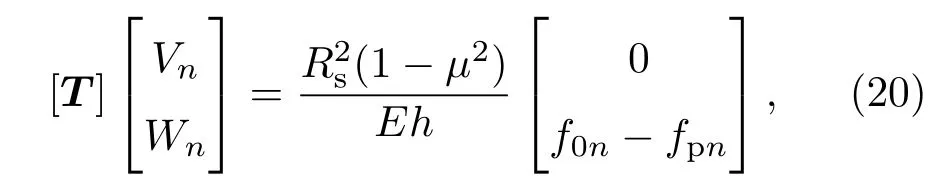
其中矩阵[T]的元素如下:T11=Ω2−n2,T12=T21=in,T22=1+K+Kn4−2Kn2−Ω2.是无量纲频率.
由(20)式可以得到仅与径向位移幅值相关的控制方程:
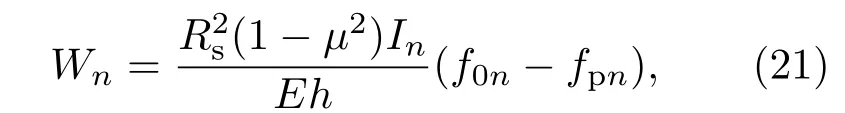
其中In=T11/det(T),In与n有关,det(T)表示矩阵[T]的行列式.
很明显,求解控制方程(21)的关键在于得到径向位移幅值Wn和壳体表面声载荷幅值fpn之间的关系.因此需要通过壳体表面流体与结构速度连续条件来求解该问题,在声固耦合交界面处.具体方程为[10]:
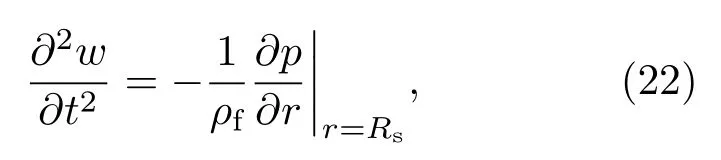
因为很难直接求解速度连续方程,采用Galerkin法进行处理,可选择的权函数有两类,一类是壳体径向位移的周向函数,另一类是声压的周向函数:
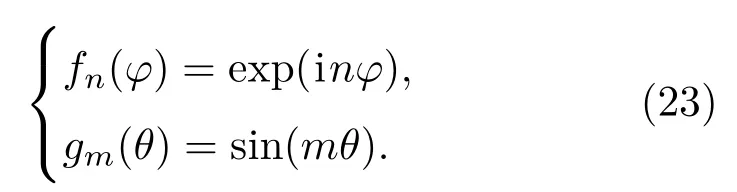
因此方程(22)可以转变为Galerkin积分的弱形式:
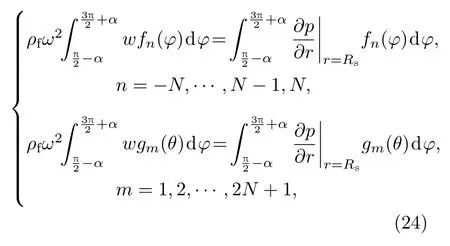
其中N是截断项数,即需要构造2N+1个积分方程.
由(24)式可以得到径向位移幅值和声压幅值之间的关系:
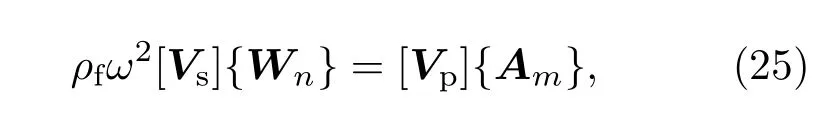
其 中[Vs]和[Vp]均 是2N+1阶 方 阵,{Wn}和{Am}分别表示径向位移幅值向量和声压幅值向量,且{Wn}=[W−N,W−N+1,···,WN−1,WN]T,{Am}=[A1,A2,···,A2N,A2N+1]T,上标T表示转置.
根据(16)式中两类坐标系的几何关系,可以将声压沿径向的导数转换到声学坐标系下:
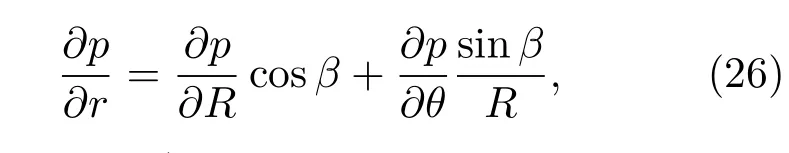
其中夹角β=3π/2−θ−φ.
由此,当权函数选择壳体径向位移的周向函数exp(inφ)时,[Vs]和[Vp]中每一个元素的具体表达式如下:
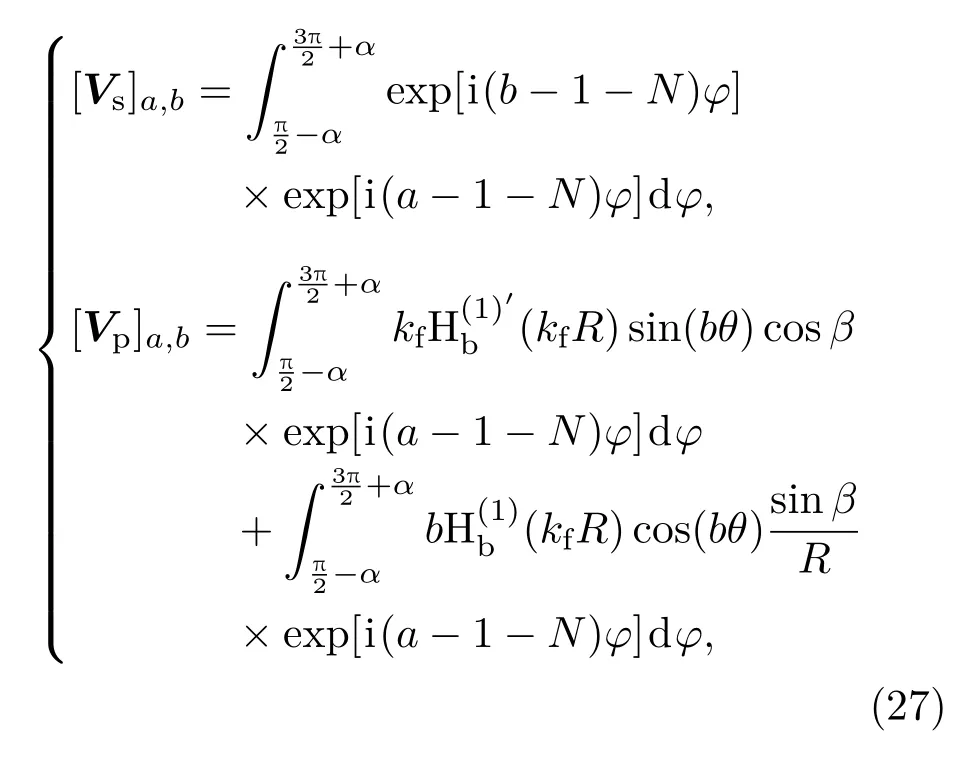
其中a,b分别表示矩阵的行和列.
当权函数选择声压的周向函数sin(mθ)时,[Vs]和[Vp]中每一个元素的具体表达式如下:
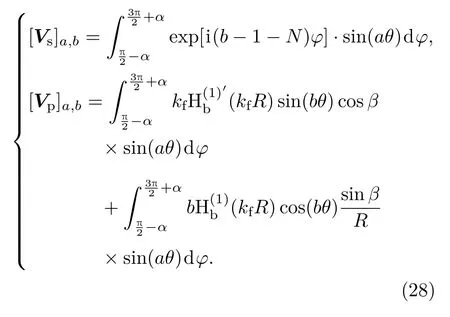
由于(27)或(28)式中积分包含汉克尔函数,无法直接进行积分计算,因此也采用(18)式中离散求和的方法来近似计算.
为了方便求解耦合方程,将(21)式改写为矩阵运算方程:
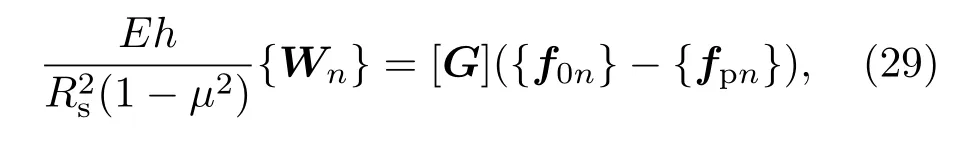
其中{f0n}=F0/2π{exp(iNφ0),exp[i(N−1)φ0],···,exp(−iNφ0)}T;[G]矩阵为对角矩阵,[G]j,j=Ij−1−N;{fpn}={fp,−N,fp,−N+1,···,fp,N}T.
同时,(15)式中{fpn}也可表示为矩阵的形式:{fpn}=[Tp]{Am}.(30)其中矩阵[Tp]中每一个元素的具体表达式如下:
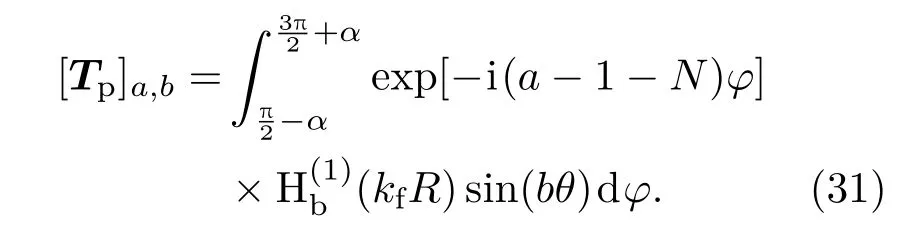
将(25)和(30)式代入方程(29)中,可以求解出径向位移幅值{Wn}:
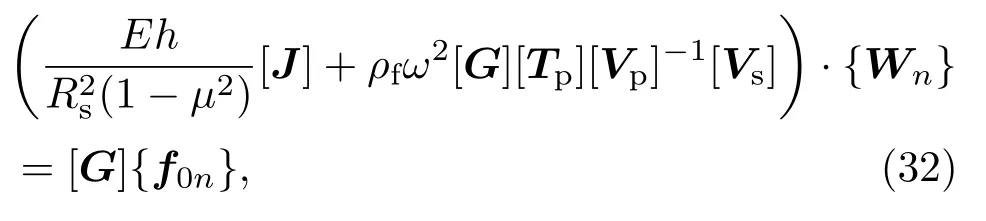
其中矩阵[J]是2N+1阶单位矩阵,并且在得到径向位移幅值{Wn}后,根据(25)式可以求解出{Am},从而可以计算声压.
前文求解受迫振动时,是已知激励力及激励频率,求响应(径向位移幅值).当求解自由振动时,并没有激励源,固有频率是要求解的未知量.由此(32)式可以表示为
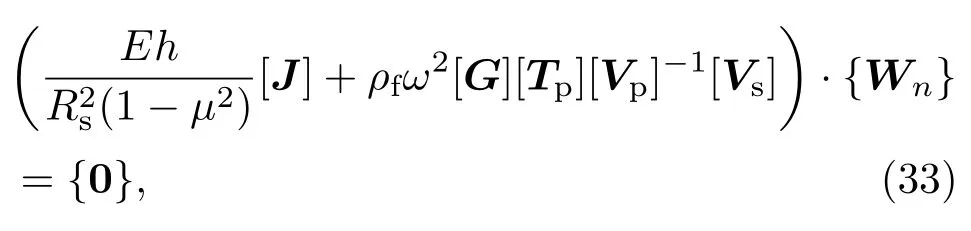
其中{0}表示零向量,显然(33)式是个典型的特征值问题,即求解角频率ω.
具体来讲就是通过定义(33)式中系数矩阵行列式值为零来求解角频率:
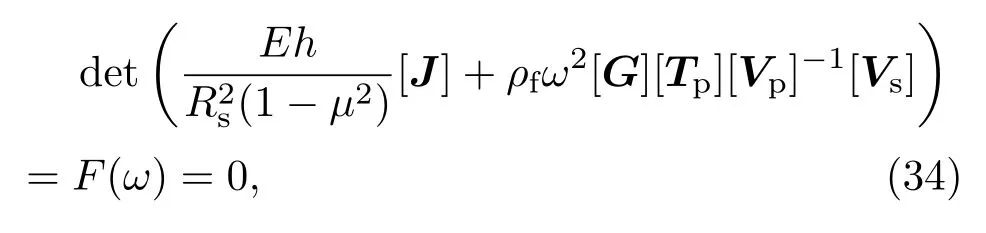
其中F(ω)表示系数矩阵的行列式值.
因为矩阵[J],[Vp],[Tp]中均含有角频率ω,实际上矩阵的行列式值F(ω)=0是个关于角频率隐式表达的超越方程,难以直接解出ω.因此本文采用搜根的方法进行求解,通过设置合适的搜根步长,逐步增大输入的角频率,当行列式值过零点时,输出对应的角频率,这个角频率即为系统的固有角频率.由此可以将超越方程的各阶角频率从小到大逐一求出,再根据可以得到各阶固有频率.
3 数值计算
模型参数:半径Rs=0.18 m,厚度h=0.001 m,壳体密度ρ=7850 kg/m3,杨氏模量E=206 GPa,泊松比µ=0.3,流体密度ρf=1025 kg/m3,流体声速cf=1500 m/s.
3.1 收敛性分析
为了说明方法的收敛性,取无量纲浸没深度H/Rs=−0.5,H/Rs=0和H/Rs=0.5,分别计算在激励力频率200,400,800 Hz时径向均方根振速Vm随截断数N的变化规律,定义
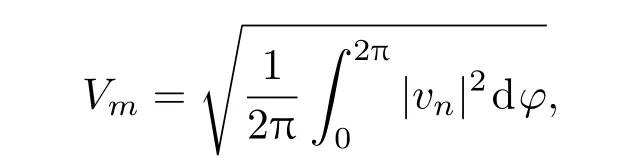
其中vn=∂w/∂t表示径向速度;则均方根速度级 VML=20lg(Vm/V0),其中基准速度V0=10−6m/s. 激励力幅值F0=1 N,激励角度φ0= π/4. 定义复杨氏模量E′=E(1+iη),结构阻尼η=0.01.计算中权函数选择位移的周向展开函数.
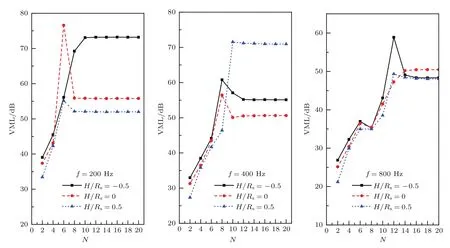
图2 均方根速度级VML收敛性分析Fig.2.Convergence analysis of the root mean square velocity levels.
从图2可见,均方根速度级随着截断项数N的增大很快趋于稳定;并且频率越高,达到收敛时截断项数N的取值越大.由图2可知,对于频率小于800 Hz时的分析计算,N取16时已足够收敛.
3.2 本文方法的适用性分析
对于Amabili[12]提出的自由液面近似处理方法,浸没角度α的适用范围仅为−π/8到π/8(无量纲浸没深度H/Rs约为−0.38—0.38,无量纲深度为负值表示壳体的圆心在自由液面上方),而本文方法的主要优势就是模型中壳体部分浸没时的浸没深度范围更广.为了验证本文的方法,无量纲浸没深度取值为−0.9—0.9,分别计算两种不同权函数下首阶固有频率值,并与有限元软件Comsol仿真计算结果进行对比.其中有限元模型如图3所示,流域以声学坐标原点为中心,半径取2 m,用完美匹配层模拟无限远声学边界,匹配层厚度取0.05 m.网格包含7980个域单元和756个边界单元.
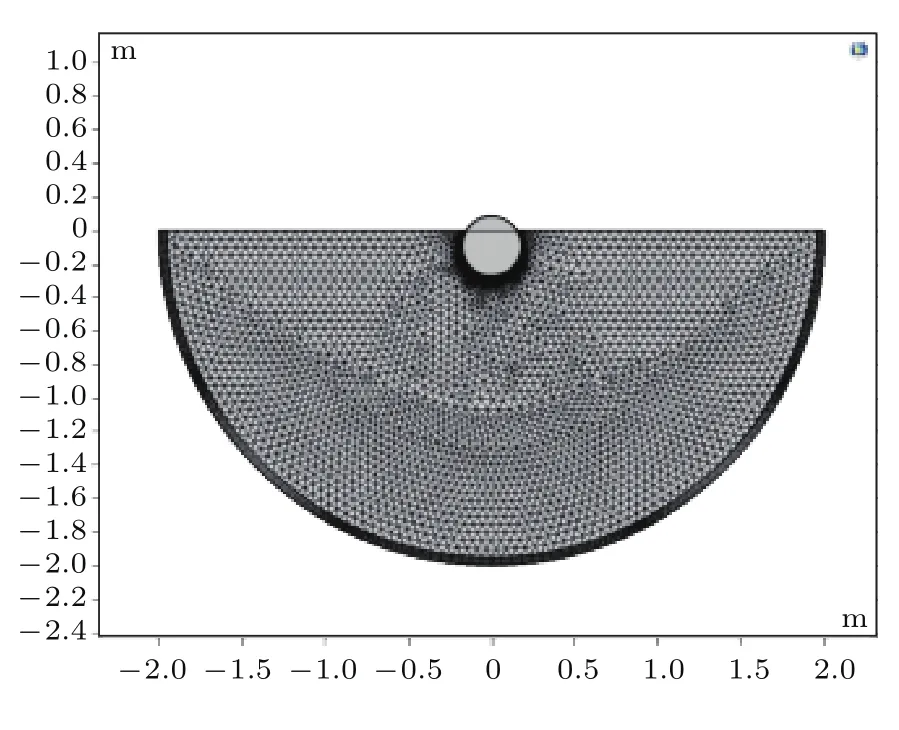
图3 有限元模型Fig.3.The finite element model.
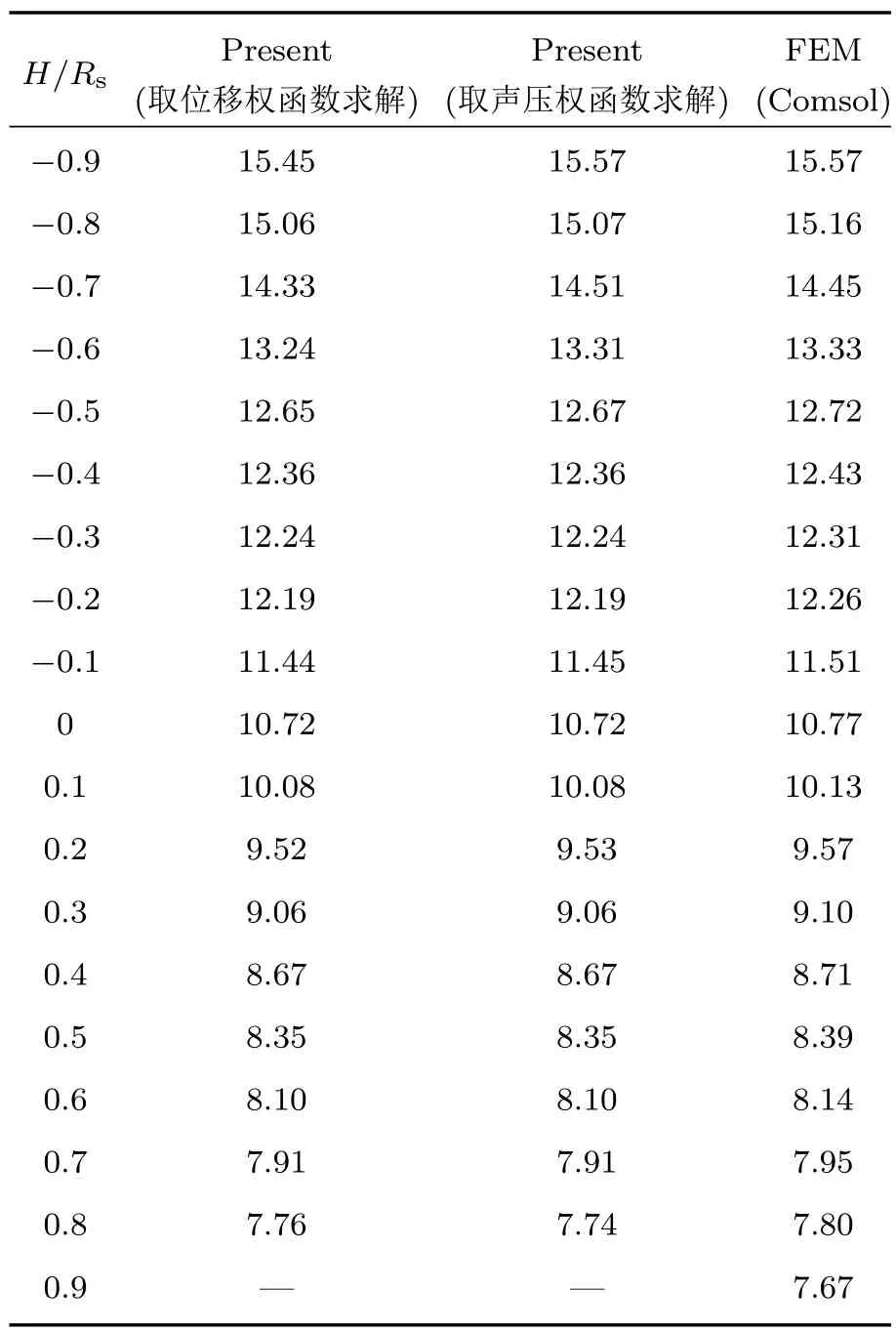
表1 不同浸没深度下首阶固有频率对比(单位为Hz)Table 1.Comparison of the fundamental frequency with dif f erent immerged depth(in Hz).
从表1可以看出,选择位移函数或者选择声压函数作为权函数时,首阶固有频率计算结果符合很好.并且无论选择哪类权函数,无量纲浸没深度H/Rs均可以从−0.9变化到0.8(当无量纲浸没深度过大或者过小时计算结果难以收敛),这表明本文的浸深适用范围非常广,方法更具有一般性.
此外,从表1还可以看出,本文方法计算结果与Comsol仿真计算结果符合良好,而且不同方法下首阶固有频率随浸没深度的变化规律也是一致的.这是由于随着壳体浸没深度的增大,流固耦合面增大,附连水质量也相应增加,因此固有频率会逐渐减小.
3.3 准确性验证
3.3.1 自由振动的验证
为说明本文方法计算自由振动问题的准确性,分别取无量纲浸没深度H/Rs=−0.7和H/Rs=0.7,计算系统前十阶固有频率,并与有限元软件Comsol仿真计算结果进行对比.定义固有频率的相对误差Error=|f1−f2|/f2×100%.
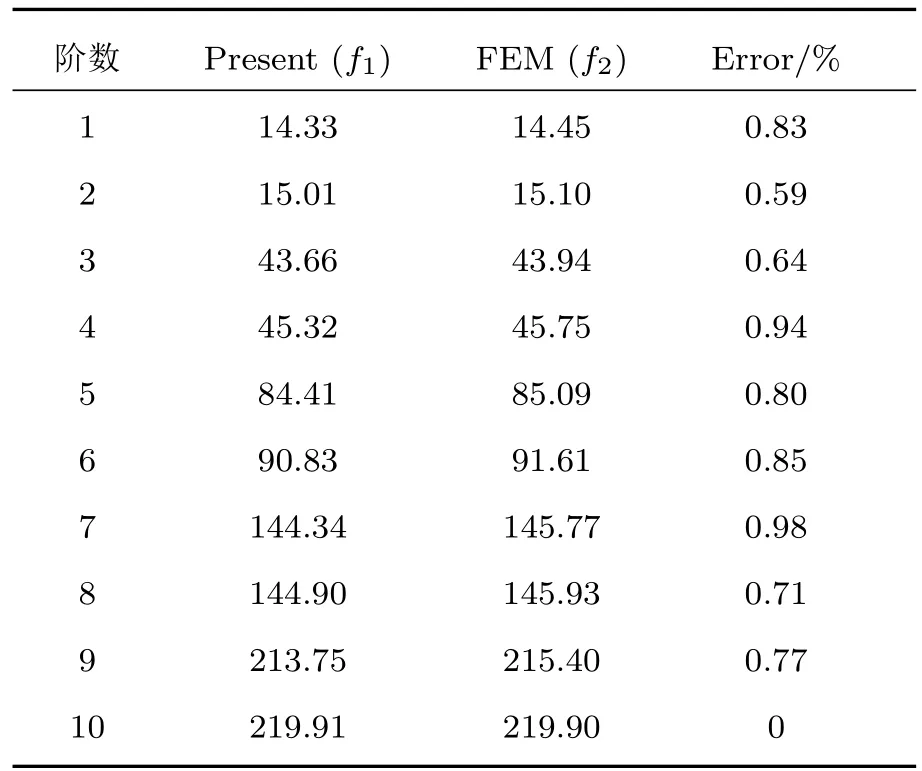
表2 H/Rs=−0.7时前十阶固有频率对比(单位为Hz)Table 2.Comparison of the the first ten order natural frequencies when H/Rs=−0.7(in Hz).
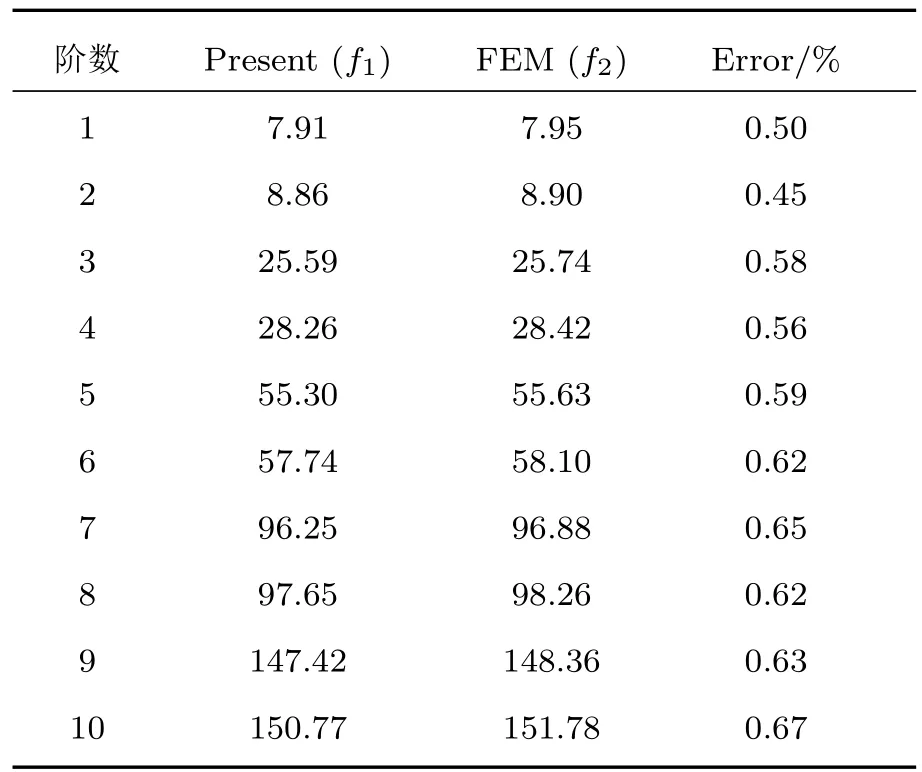
表3 H/Rs=0.7时前十阶固有频率对比(单位为Hz)Table 3.Comparison of the the first ten order natural frequencies when H/Rs=0.7(in Hz).
从表2和表3可以看出,本文方法计算得到的前10阶固有频率值与Comsol仿真计算结果符合良好,最大相对误差不超过1%,说明采用本文方法计算固有频率是准确可靠的.
3.3.2 受迫振动的准确性验证
在分析完自由振动的准确性之后,进一步分析受迫振动的准确性. 取无量纲浸没深度H/Rs=−0.5和H/Rs=0.5,计算在激励力频率50—500 Hz时测点径向速度(频率间隔10 Hz),定义径向速度级VL=20×log(|V|/V0),其中V为径向速度,基准速度V0=10−6m/s.激励力幅值F0=1 N,激励角度φ0=0.测点位于周向角φ=π处.
从图4可以看出,本文计算结果和Comsol仿真计算结果整体符合良好,说明本文方法分析受迫振动是准确可靠的.但是当频率较高时(以图4为例,大于400 Hz),误差逐渐增大.主要的原因可能是有限元计算声固耦合问题时,随着频率增大,对网格密度的要求也提高,计算精度会降低.
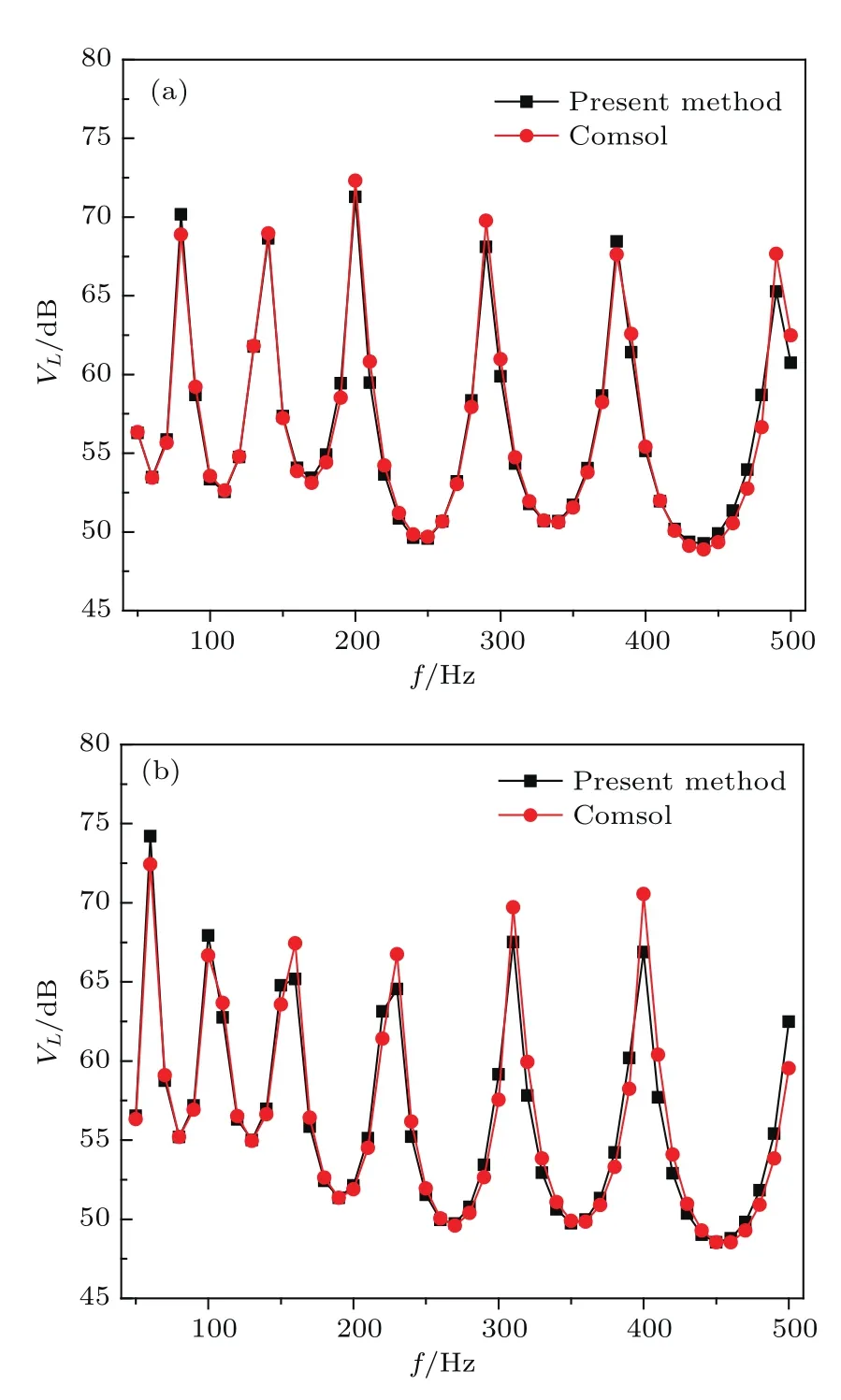
图4 不同方法下径向速度级对比 (a)H/Rs=−0.5;(b)H/Rs=0.5Fig.4.Comparison of the radial velocity levels with dif f erent methods:(a)H/Rs=−0.5;(b)H/Rs=0.5.
3.3.3 声场求解的准确性验证
为进一步说明本文方法计算声场也是准确的,取无量纲浸没深度H/Rs=−0.4和H/Rs=0.4,计算激励频率为50 Hz时声压幅值云图,并与Comsol仿真计算结果进行对比.其中激励力幅值F0=1 N,激励角度φ0=0,云图尺寸为1.2 m×0.6 m.
从图5和图6可以看出,本文方法计算得到的声压云图和有限元软件Comsol仿真计算结果符合良好,由此可以说明本文方法计算声场是准确可靠的.
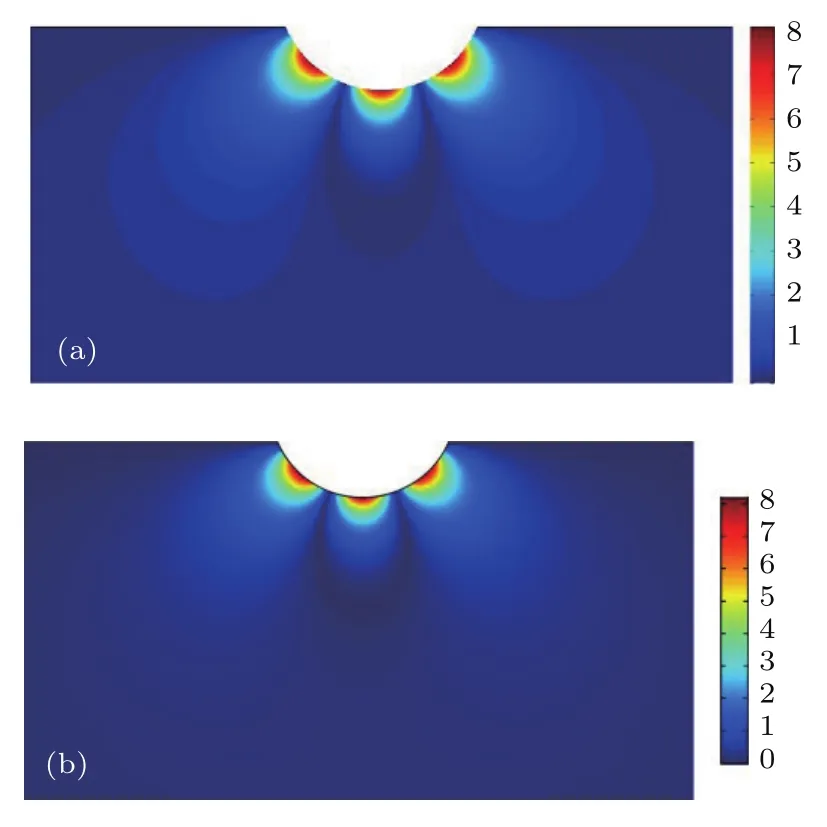
图5 H/Rs=−0.4时不同方法下声压幅值云图对比 (a)本文方法;(b)Comsol仿真Fig.5.Comparison of the sound pressure contour map with dif f erent methods when H/Rs=−0.4:(a)Present method;(b)Comsol.
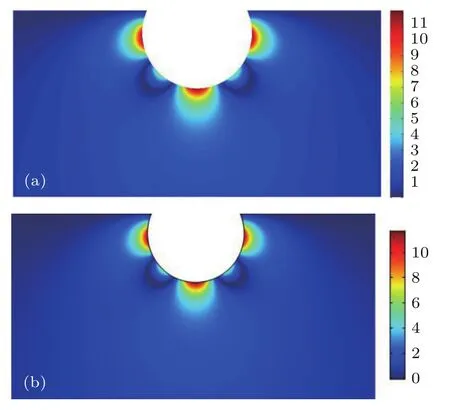
图6 H/Rs=0.4时不同方法下声压幅值云图对比 (a)本文方法;(b)Comsol仿真Fig.6.Comparison of the sound pressure contour map with dif f erent methods when H/Rs=0.4:(a)Present method;(b)Comsol.
此外,值得一提的是,本文方法计算效率也非常高,以图5或图6中声压云图的计算为例,在Matlab中仅仅需要不到2 s即可计算出精确稳定的结果.
4 讨 论
在验证了本文方法计算声固耦合系统振动及声压求解均准确可靠之后,进一步分析与讨论部分浸没壳体的模态振型、无量纲浸没深度对受迫振动的影响以及远场声压的指向性特征.
4.1 模态振型分析
为了更直观地揭示声固部分耦合系统自振特性,取无量纲浸没深度H/Rs=0.7和无限域时计算得到的前4阶模态振型及固有频率.
对比表4和表5可以看出,部分浸没工况下振型与无限域振型有差异.以H/Rs=0.7时第一阶振型为例,振型函数约为cos2φ+0.25·cosφ−0.05·cos3φ,而对于无限域壳体,对应的振型函数为cos2φ(规则的周向波型).这是由于流体在周向分布不均,壳体与结构的部分耦合破坏了圆柱壳的周向的对称性,故规则的周向波之间会发生互耦,形成复杂的振型函数.
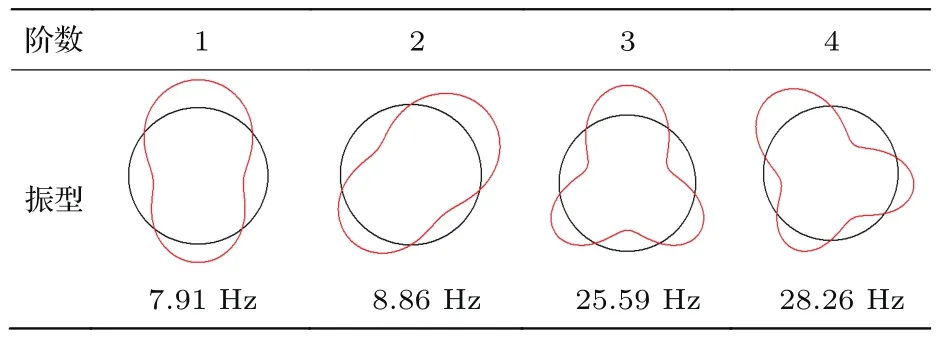
表4 H/Rs=0.7时前4阶模态振型Table 4.Modal shapes of the first four orders when H/Rs=0.7.
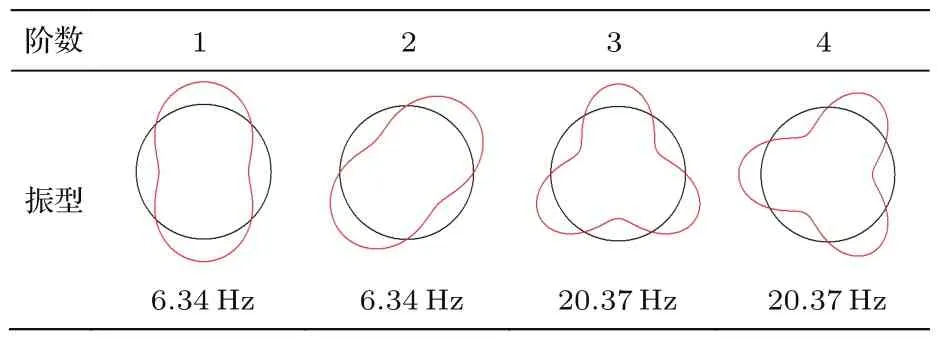
表5 无限域时前4阶模态振型Table 5.Modal shapes of the first four orders when in infinite fluid.
此外,由于自由液面的存在,系统仅有惟一对称轴,对称和反对称模态固有频率也存在差异.以H/Rs=0.7算例下前两阶固有频率为例,分别为7.91 Hz和8.86 Hz,有明显差异;但是对于无限域情况,由于系统具有周向对称性,对称和反对称模态固有频率是相同的,二者存在明显区别.
另外,部分浸没工况下,对称和反对称模态振型函数之间的周向波互耦程度也不尽相同.仍以H/Rs=0.7工况为例,第二阶振型函数(反对称)约为sin2φ+0.38·sinφ−0.08·sin3φ,函数各成分之间的比值由对称模态时1:0.25:−0.05变为反对称时1:0.38:−0.08.而对于无限域情况,对应的振型函数为sin2φ,这也是系泊状态下自振特性区别于无限域工况的又一特征.
4.2 均方根振速频谱分析
3.2节中提到,随着浸没深度增大,流固耦合面会增大,附连水质量也会相应增加.为进一步解释这个观点,本文选取了H/Rs=−0.6,−0.3,0,0.3,0.6这五个深度,对比分析各工况下均方根速度级的频谱曲线.激励力幅值F0=1 N,激励角度φ0=0,激励频率为1—100 Hz,扫频间隔1 Hz.
从图7可以看出,随着浸没深度增大(液面升高),共振峰均向低频移动.这也是因为浸没深度增大使得附连水质量增大,从而增加了系统的总质量,导致共振频率降低,频谱曲线整体左移.
4.3 远场声压指向性分析
系泊状态下的舰船等目标的水下辐射噪声对于其隐蔽性有着重要意义.因此,本节进一步开展二维系泊圆柱壳远场声压指向性特征的研究.
取无量纲浸没深度H/Rs=−0.5,0,0.5,分别计算激励频率f=100,200 Hz时远场声压级指向性图.其中激励力幅值F0=1 N,激励位置φ0=π/4.远场点取自声学坐标系,半径R=1000 m,角度θ取0—π,取值间隔θ/180.定义声压级SPL=20lg(|p|/p0),其中基准声压p0=10−6m/s.
从图8可以看出,所有声压指向性曲线都在角度θ=π/2时(正下方)取最大值.而且尽管激励位置并不在壳体的垂直对称轴上,但声压级关于垂直对称轴呈对称分布.以下对这些现象进行物理解释.
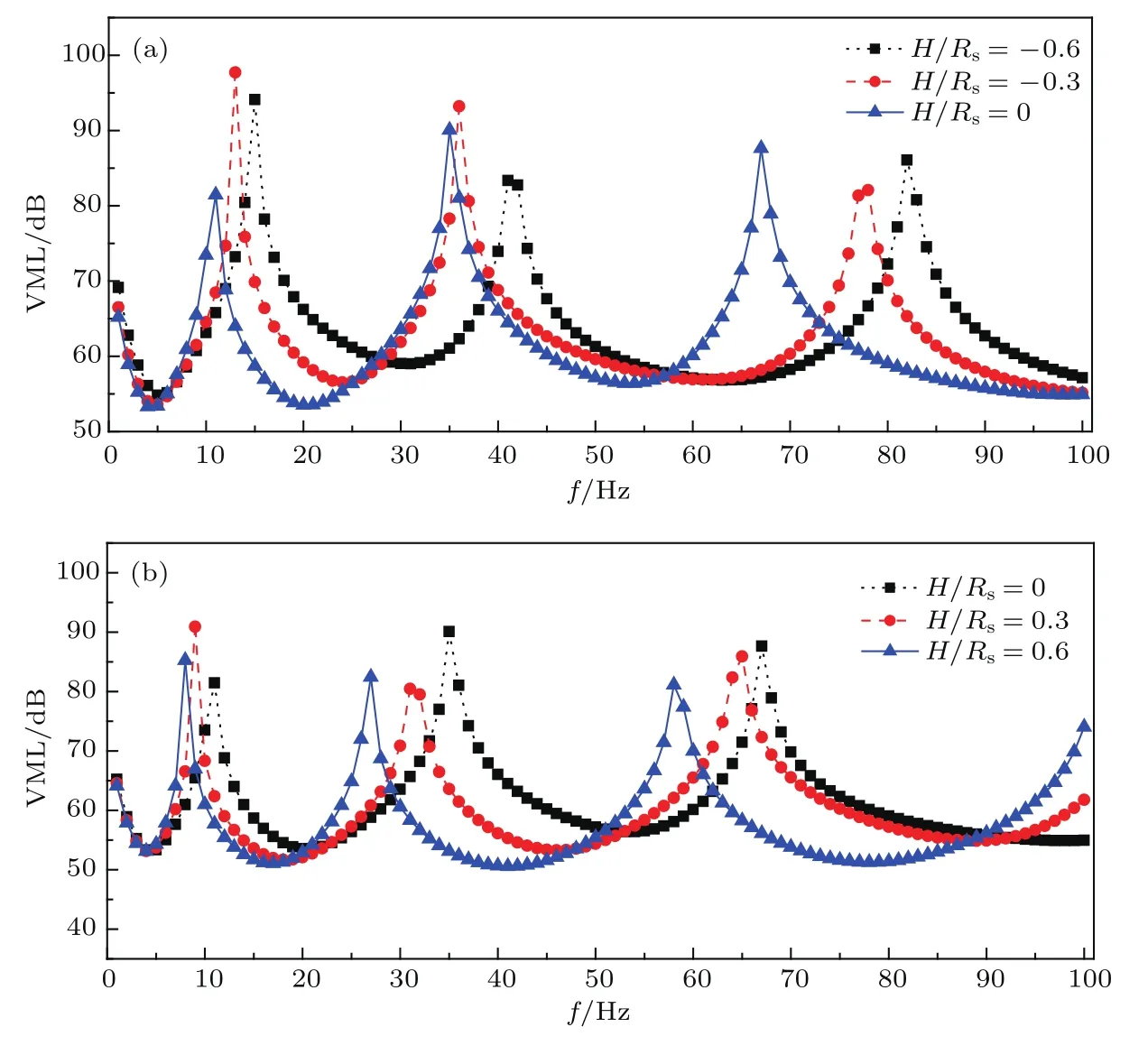
图7 不同浸没深度下均方根速度级频谱曲线 (a)H/Rs=−0.6,−0.3,0;(b)H/Rs=0,0.3,0.6Fig.7.Spectrum curves of the root mean square velocity levels at dif f erent immersion depths:(a)H/Rs=−0.6,−0.3,0;(b)H/Rs=0,0.3,0.6.
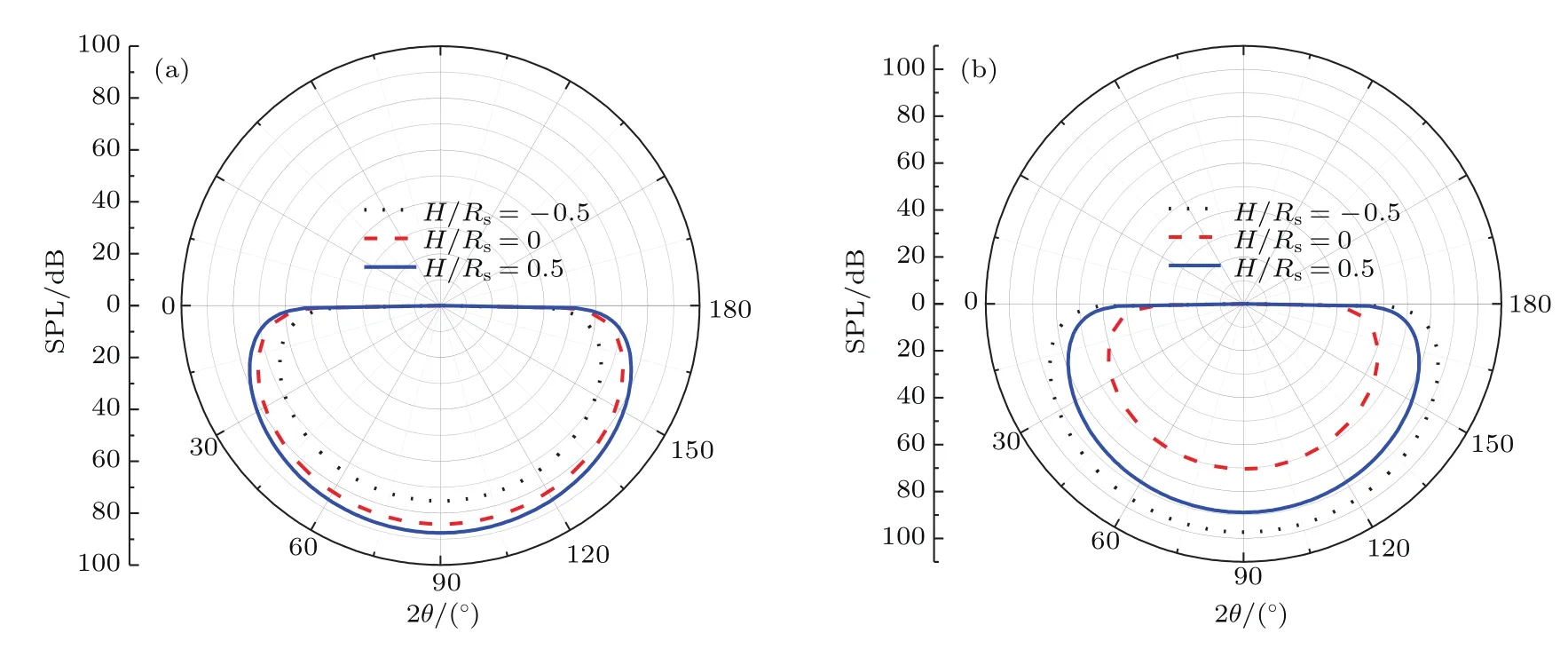
图8 不同浸没深度下声压级指向性 (a)f=100 Hz;(b)f=200 HzFig.8.Directivity of the sound pressure levels at dif f erent immersion depths:(a)f=100 Hz;(b)f=200 Hz.
因为研究的场点位于远场,从几何上讲,壳体湿表面上任意一点到场点的距离可以认为是近似相同的.由此水下的辐射面可以等效为一个点源,而且这个点源距离自由液面的距离在0—2Rs之间(这个距离与速度分布有关,是未知的).
基于镜像原理[8],自由液面对水下声场的作用可以通过在自由液面的另一侧构造等距的(虚源到液面距离)以及反相位的虚源来实现.则水下声场可以认为是由实源和虚源共同贡献,且虚源和实源共同作用下声压在自由液面上满足为零的条件.实际上,由于实源和虚源距离较近,在低频下,这样的物理模型构成了偶极子模型.由此,可以得到声偶极模型的数学表达式[8]:
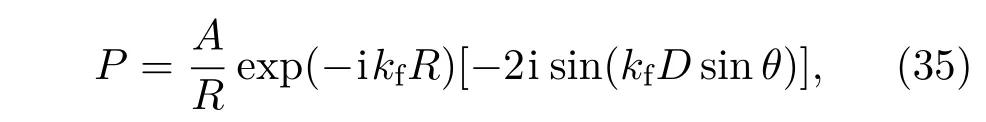
其中A表示点源的声压幅值,R代表场点到声学坐标原点的距离,D表示点源与镜像源距离(D/Rs<4).
虽然D值是未知的,但并不影响分析声压的指向性.因为当激励频率不太高时,kf和D的乘积是小于π/2的.因此当远场点位于壳体截面圆心正下方时(θπ/2),从(35)式可以看出,声压幅值将取最大值.此外,从(35)式中正弦三角函数的数学性质也可以看出,声压级曲线关于对称轴(θ=π/2)将呈对称分布,这也很好地契合了图8中声压级指向性曲线的特征.
5 结 论
提出了一种求解系泊状态下圆柱壳声振问题的新方法.通过将声压与壳体位移建立在不同的坐标系下,方便地得到了其解析表达式,然后再利用Galerkin法以及坐标变换关系处理声固耦合界面的速度连续条件,最终可以很便捷、高效地求解该浮态系统的声振特性,也为求解半空间中弹性结构与声场部分耦合的声振问题提供了新的思路.具体结论如下.
1)通过对部分浸没壳体的自由、受迫振动和辐射声压的求解并与有限元数值解进行对比分析,验证了本文方法的准确性,且本文方法能适用于浸没深度更大范围变化的一般情况.
2)随着自由液面的升高和下潜深度的增大,流体与结构耦合交界面积增大,导致附连水质量相应增大,从而整个系统的附连水质量也会增大,因此同阶次固有频率会逐渐减小.
3)部分浸没工况下自振特性分析时,流体与结构处于部分耦合的状态,从而导致由结构传递到声场中的声波碰到声学边界产生回波,叠加形成复杂的声场.流体介质对声场的作用以声负载的形式作用于结构表面,导致结构的周向波发生互耦,由此结构的周向模态振型不再是规则的波型.
4)由于自由液面的存在使得整个耦合系统仅有惟一对称轴,从而破坏了圆柱壳振动在周向的任意对称性.因此结构的对称和反对称模态的固有频率会有明显差异.
5)由于类偶极子效应,辐射声波以及由边界反射的声波发生干涉.当激励频率相对较低时,根据相干波叠加函数的性质,远场声压级的最大值总是出现在结构正下方.
[1]Williams W,Parke N G,Moran D A,Sherman C H 1964J.Acount.Soc.Am.36 2316
[2]Harari A,Sandman B E 1976J.Acoust.Soc.Am.60 117
[3]Fuller C R 1988J.Sound Vib.122 479
[4]Pan A,Fan J,Wang B,Chen Z G,Zheng G Y 2014Acta Phys.Sin.63 214301(in Chinese)[潘安,范军,王斌,陈志刚,郑国垠2014物理学报63 214301]
[5]Liu P,Liu S W,Li S 2013Ship Sci.Technol.36 36(in Chinese)[刘佩,刘书文,黎胜 2013舰船科学技术 36 36]
[6]Huang H 1981Wave Motion3 269
[7]Hasheminejad S M,Azarpeyvand M 2005J.Appl.Math.Mech.85 66
[8]Bai Z G,Wu W W,Zuo C K,Zhang F,Xiong C X 2014J.Ship Mech.18 178(in Chinese)[白振国,吴文伟,左成魁,张峰,熊晨熙2014船舶力学18 178]
[9]Guo W J,Li T Y,Zhu X,Miao Y Y,Zhang G J 2017J.Sound Vib.393 338
[10]Guo W J,Li T Y,Zhu X,Zhang S 2017Chin.J.Ship Res.12 62(in Chinese)[郭文杰,李天匀,朱翔,张帅2017中国舰船研究12 62]
[11]Amabili M 1996J.Sound Vib.191 757
[12]Amabili M 1997J.Vib.Acoust.119 476
[13]Ye W B,Li T Y,Zhu X 2012Appl.Mech.Mater.170 2303
[14]Selmane A,Lakis A A 1997J.Sound Vib.5 111
[15]Ergin A,Temarel P 2002J.Sound Vib.254 951
[16]Krishna B V,Ganesan N 2006J.Sound Vib.291 1221
[17]Hidalgo J A,Gama A L,Moreire R M 2017J.Sound Vib.408 31
[18]Escaler X,Torre O D,Goggins J 2017J.Fluid Struct.69 252
[19]Li T Y,Wang P,Zhu X,Yang J,Ye W B 2017J.Vib.Acoust.139 041002
[20]Li H L,Wu C J,Huang X Q 2003Appl.Acoust.64 495
[21]Li T Y,Wang L,Guo W J,Yang G D,Zhu Xiang 2016Chin.J.Ship Res.11 106(in Chinese)[李天匀,王露,郭文杰,杨国栋,朱翔2016中国舰船研究11 106]
[22]Zhu X,Ye W B,Li T Y,Chen C 2013Ocean Eng.58 22

