一类二次多项式混沌及其随机数生成器设计

朱淑芹，王文宏，李俊青

ZHU Shuqin,WANG Wenhong,LI Junqing

聊城大学 计算机学院，山东 聊城 252059

School of Computer Science,Liaocheng University,Liaocheng,Shandong 252059,China

1 引言

混沌作为一种特有的非线性动力学现象，具有对初始状态和系统参数的极端敏感性、运动轨道的长期不可预测性、遍历性、混合性等特性[1]，利用混沌的这些特性可以生成伪随机序列，只要混沌系统和初值确定产生的伪随机序列就确定，因此这种伪随机序列具有可重复性。用混沌系统构造伪随机数发生器已成为信息安全领域的研究热点。王雪、闵乐泉[2]等基于八维混沌广义同步系统构造了一个伪随机数发生器。张丽娇[3]和韩双霜[4]分别基于Marotto定理构造了一个二维和三维的离散混沌映射，然后在新混沌映射的基础上分别设计了一个伪随机数发生器。朱淑芹、李俊青等[5]基于Marotto定理构造了一个四维的离散混沌映射并在此基础上设计了一个伪随机数生成器。Chen E，Min Lequan[6]构造了一类四维离散混沌系统，在四维离散混沌系统的基础上利用广义同步理论构造出八维离散混沌系统，基于八维混沌系统构造出一个伪随机数生成器。文献[2-6]中随机数生成器的设计都是把混沌系统产生的随机实数，通过一个实数域到整数域的变换来实现的。而文献[7]和文献[8]采用区间划分的方法来设计随机数生成器，将混沌系统的值域区间划分为m个不相交的区域，并为每个区域标识惟一的数字0～(m-1)，通过判断混沌轨道进入哪个区间来生成随机数。另外，还可以采用把混沌系统生成的实数随机数进行二进制化的方法来产生伪随机数[9-10]。

随机数生成器生成的随机数好坏的关键指标是随机性、独立性、均匀分布性等特性[11]。由于目前对于任意的混沌系统还不能借助概率论方法对混沌系统长期的统计特征进行刻画描述，即不能用混沌映射的概率密度来描述，所以混沌系统生成的随机数的独立性、均匀分布性的特性的判断依赖于实验模拟结果，缺乏理论证明。混沌系统中，只有Chebyshev映射、Tent映射、Logistic映射等几个简单的混沌映射的概率密度是已知的。何振亚、李克等[12]给出了Logistic映射与Tent映射的拓扑共轭关系以及Chebyshev映射与Tent映射的拓扑共轭关系，并由此推出了Logistic映射和Chebyshev映射的概率密度。徐正光、田清[13]等构造了一类与Tent映射拓扑同构的混沌系统。本文在此基础上进一步推广了文献[13]的结论，构造了一类与Tent映射拓扑共轭的二次多项式混沌映射，该二次多项式混沌映射具有三个系统参数，并给出了该类混沌映射的概率密度函数。然后，根据对应的概率密度函数，设计了一个反正弦函数，通过反正弦函数变换，使二次多项式混沌映射生成的随机数在区间（-0.5，0.5）上服从均匀分布，最后利用区间划分的方法设计了一个能生成{0，2m-1}的伪随机数发生器。理论分析和实验结果表明该随机数发生器生成的随机序列具有较好的初值敏感性、自/互相关特性，并通过了NIST SP800-22随机数检测。

2 一类二次多项式混沌映射及其概率密度

定义1[14]对于分别定义在I和J上的两个映射（1）和映射（2）：

若存在一个连续、可逆的函数h，即 y=h(x)，x=h-1(y),x∈I，y∈J，使得，则称映射 f和g关于h拓扑共轭。

f(x)与Tent映射关于函数h(x)是拓扑共轭的。

证明 由于Tent映射为：

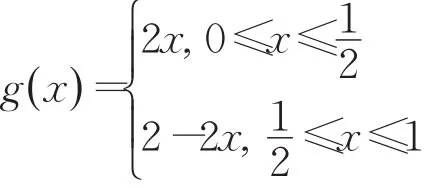
根据定义1，一方面

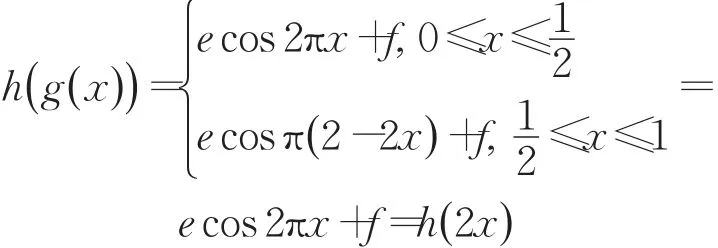
另一方面

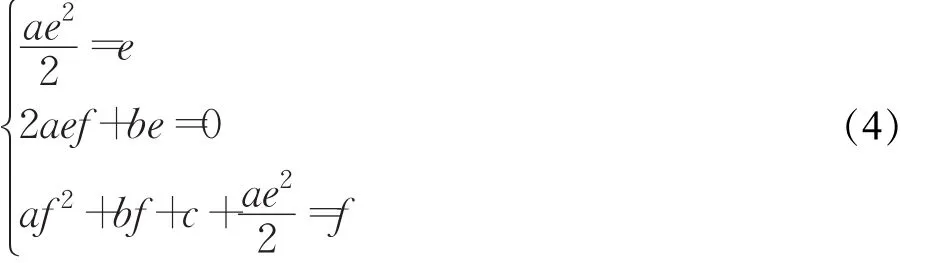
由于e≠0，简化式子（4），可得式子（3）。证明完毕。

刘新波[15]等指出两拓扑共轭的映射具有相同的Lyapunov指数，因此只要 f(x)中的参数满足式（3）的条件，f(x)的Lyapunov指数与Tent映射的Lyapunov指数相同，为ln2。因此 f(x)为混沌系统。

本文中由定理1产生的二次多项式混沌映射记为：

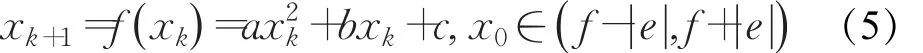
其中，参数 a、b、c、e、f满足定理1的条件。

引理1[14]如果映射 f(x)和g(x)关于函数h(x)拓扑共轭，ρg(x)是映射g(x)的概率密度函数，那么映射f(x)的概率密度函数为：

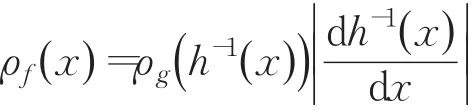
其中，参数 a、b、c、e、f满足定理1的条件。

证明 已知Tent映射的概率密度函数为：

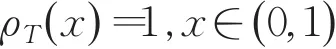
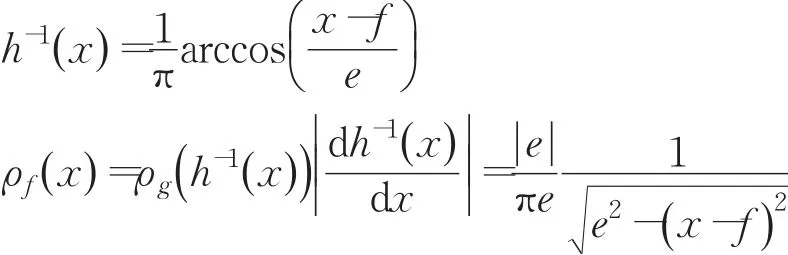
由定理2可知二次多项式混沌映射（5）产生的序列不是均匀分布的，具有明显的统计特性。可以通过一个非线性变换，把混沌映射（5）产生的非均匀分布的随机序列转化为均匀分布的随机序列。

定理3混沌映射（5）产生的随机变量记为X，则随机变量

在（-0.5，0.5）上服从均匀分布。

证明 由定理2可知随机变量X的概率密度函数为：

则随机变量Z的分布函数：

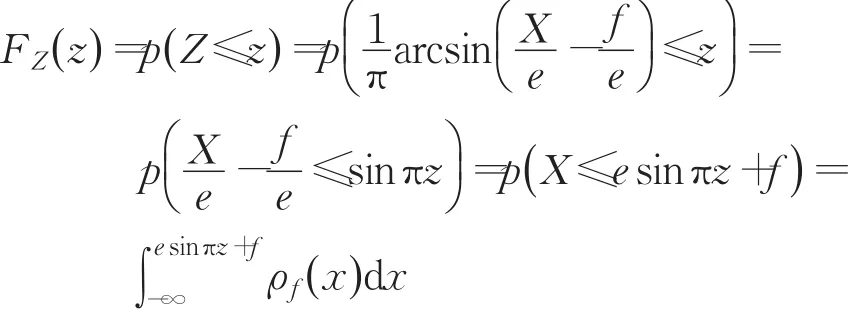
对等式两边关于参数z求导：

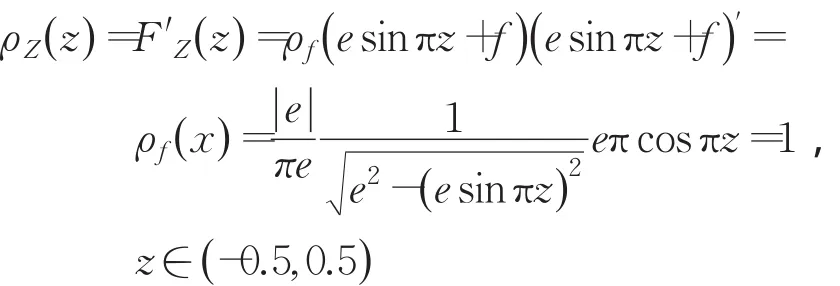
故随机变量Z的密度函数为：

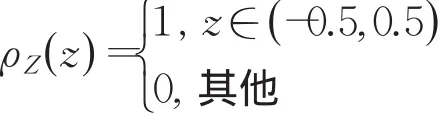
证明完毕。

3 基于二次多项式混沌映射的伪随机数生成器的设计

由前面的定理3可知二次多项式混沌映射生成的随机序列X经过一个反正弦变换得到随机序列Z，Z在区间（-0.5，0.5）上服从均匀分布，因此本文利用区间划分的方法设计伪随机数发生器，这样产生的随机数的随机性、均匀性和独立性更好。具体步骤如下：

（1）由混沌映射（5）生成随机序列X={x1,x2,…,xn}。

（3）把区间（-0.5，0.5）等分为 N=2m个子区间 τi，0.5。如果 zk∈τi,那么sk=i。则就是生成的混沌密钥流。

由定理3可知Z在区间（-0.5，0.5）上服从均匀分布，上述方法产生的密钥流是随机的、独立的、均匀的。

4 实例仿真

实例1根据定理1的条件取a=2，b=-2，c=0，e=1，f=0.5。则得到的一个离散混沌映射为：

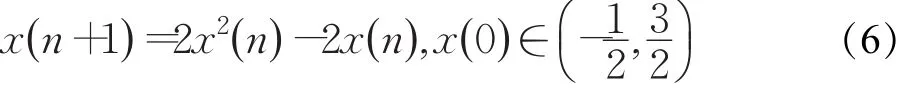
则混沌映射式（6）关于函数h(x)与Tent映射拓扑共轭，其中：

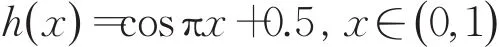
混沌映射式（6）的概率密度函数为：

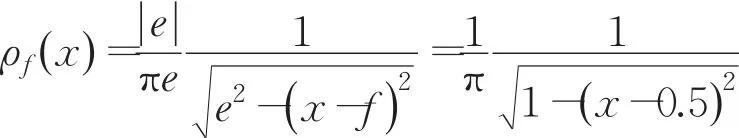
取初值 x0=0.43，迭代公式（6）6 000次的结果如图1。从图中可以看出迭代值布满整个区间，说明系统（6）具有伪随机、有界性、遍历性等混沌特性。

图1 混沌映射（6）的迭代结果

实例2 根据定理1的条件取a=-3，b=6，c=-4/3，e=-2/3，f=1。则得到的一个离散混沌映射为：

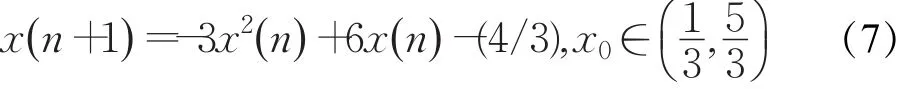
则混沌映射式（7）关于函数h(x)与Tent映射拓扑共轭，其中：

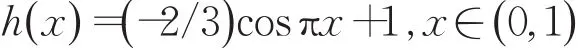
混沌映射式（7）的概率密度函数为：

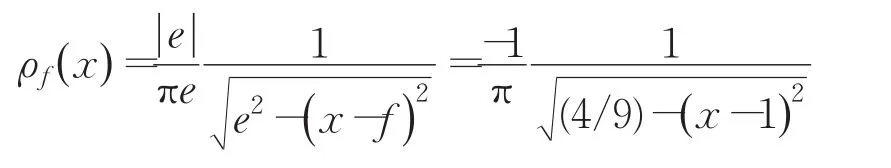
取初值x0=1.23，迭代公式（7）6 000次的结果如图2。从图中可以看出迭代值布满整个区间，说明系统（7）具有伪随机、有界性、遍历性等混沌特性。

图2 混沌映射（7）的迭代结果

5 混沌伪随机数生成器的性能分析

按照第2章生成随机数的方法，取m=8，迭代30 000次，则混沌映射（7）生成{0，1，2，…，255}的随机序列。本文对随机序列进行信息熵分析、初值敏感性分析、相关性分析和NIST SP 800-22检测以验证生成的随机数的均匀性、复杂性和随机性。

5.1 信息熵分析

香农提出信息熵的概念，用于表征信源的不确定性程度。本文用信息熵度量序列的不确定性程度。信息熵的计算公式为：

其中，pi为si出现的概率。当序列的概率分布为等概率分布时，即取[0，255]之间每一个值概率均为1/256时，具有最大熵为8 bit。经计算序列的信息熵为7.988 0bit.非常接近理想值。也可以从序列的直方图看出序列分布的均匀性。图3是随机序列S的数值分布曲线。图中横坐标代表随机序列S可能取的{0，1，…，255}中的256个数，纵坐标代表随机序列S中取{0，1，…，255}中每个数的频数。由图3可以看出随机序列S分布均匀，伪随机性良好。

5.2 初值敏感分析

对于系统（7）选择初始值 x(0)=1.23+10－15，生成的长度为30 000的{0，1，2，…，255}的随机序列，转换为240 000个二进制序列。选择初始值x(0)=1.23，生成的长度为30 000的{0，1，2，…，255}的随机序列，转换为240 000个二进制序列。序列与序列{Sk}的不同率达到49.97%，二者的相关系数为0.005 9。当两个序列的长度为320 000时，不同率达到50.07%，非常接近理想值50%。二者的相关系数为0.004 9。由此可知即使初值有微小的扰动，得到的两个序列完全不同，且两个序列完全独立。

图3 随机序列S的数值分布曲线

5.3 相关性分析

相关特性是混沌序列用于密码学的一个重要性质。理想伪随机序列的自相关函数为δ函数，互相关函数为0。对于系统（7）产生的{Sk}和{Tk}两伪随机序列。序列均值定义为：

其自相关函数定义为：

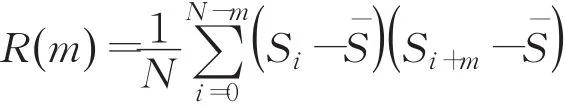
互相关函数定义为：

其中m为相关间隔。图4为两个序列的自相关和互相关函数，截取的相关间隔为0～1 000。由图4可见，自相关函数非常近似于δ函数，互相关函数最大偏差为0.005 4。因此，该伪随机序列具有良好的自相关和互相关特性。

5.4 伪随机性检测

目前具有代表性的检测标准有NIST的FIPS140-2标准、SP800-22标准、德国资讯安全联合办公室发布的AIS31标准和Marsaglia的Diehard battery检测等。一般认为，通过了这些检测的伪随机序列具有良好的伪随机性能。本文采用了目前世界上应用比较广泛的SP800-22标准来检测所产生的二进制序列的伪随机性。对于生成的长度为30 000的{0，1，2，…，255}的随机序列转换为240 000个二进制序列，进行NISTSP800-22的16项指标测试，每项的测试结果均转换为P值进行判断。表1测试结果中P值均大于显著性水平a=0.05。表1表明测试满足SP800-22的随机性要求。

图4 两个序列的自相关和互相关函数

表1 SP800-22检验结果

6 结论

本文构造了一类与Tent映射拓扑共轭的具有三个系统参数的二次多项式混沌映射，基于此类混沌映射设计了一个能生成{0,2m-1}的伪随机数发生器。理论分析和实验结果表明该随机数发生器生成的随机序列具有较好的初值敏感性、自/互相关特性，并通过了NIST SP800-22随机数检测。为产生独立、均匀、复杂的随机数提供了更多的非线性系统选择。

参考文献：

[1]方锦清.驾驭混沌与发展高新技术[M].北京：原子能出版社，2002：31-32.

[2]王雪，闵乐泉，赵耿，等.基于八维混沌广义同步系统的伪随机数发生器[J].计算机应用，2015，35（S2）：49-52.

[3]张丽娇，闵乐泉，韩双霜.二维新混沌系统和伪随机数生成器的设计[J].计算机工程与设计，2014，35（4）：1178-1182.

[4]韩双霜，闵乐泉，韩丹丹.一种基于三维离散混沌映射的伪随机数生器[J].华中科技大学学报：自然科学版，2013，41（8）：16-19.

[5]朱淑芹，李俊青，葛广英.基于一个新的四维离散混沌映射的图像加密新算法[J]，计算机科学，2017，44（1）：188-193.

[6]Chen E，Min Lequan.Discrete chaotic systems with oneline equilibria and their application to image encryption[J].International Journal of Bifurcation and Chaos，2017，27（3）：1-17.

[7]李家标，曾以成，陈仕必，等.改进型Hénon映射生成混沌伪随机序列及性能分析[J].物理学报，2011，60（6）：126-130.

[8]孙福艳，吕宗旺.空间混沌序列的加密特性研究[J].物理学报，2011，60（4）：60-65.

[9]Smaoui N，Kanso A.Cryptography with chaos and shadowing[J].Chaos，Solitons and Fractals，2009，42（4）：2312-2321.

[10]Kocarev L，Jakimoski G.Pseudorandom bits generated by chaotic maps[J].IEEE Transactions on Circuits&Systems I Fund，2003，50（1）：123-126.

[11]罗松江，丘水生，骆开庆.混沌伪随机序列的复杂度的稳定性研究[J].物理学报，2009，58（9）：6045-6049.

[12]何振亚，李克，杨绿溪.具有良好安全性能的混沌映射二进制序列[J].电子科学学刊，1999，21（5）：646-651.

[13]徐正光，田清，田立.一类可以产生独立同分布密钥流的混沌系统[J].物理学报，2013，62（12）：120501.

[14]郝柏林.从抛物线谈起：混沌动力学引论[M].2版.北京：北京大学出版社，2013：114-118.

[15]刘新波，赵德安，朱志宇.混沌映射的保密性能分析[J].江苏科技大学学报：自然科学版，2006，20（4）：51-54.