北京平原南口—孙河断裂南段第四纪活动性及其构造意义

白凌燕，李 潇，秦浩敏，张晓亮，张悦泽

(1.北京市地质调查研究院，北京 100195；2.北京市地质矿产勘查开发局 信息中心，北京 100195；3.中国地质大学(北京) 地球科学与资源学院，北京 100083)

0 引 言

北京平原地区主要活动断裂有北东向及北西向两组。北东向活动断裂自西向东有黄庄—高丽营断裂、顺义断裂、南苑通县断裂、夏垫断裂等主要活动断裂；北西向主要断裂为南口—孙河断裂。上新世以来，在区域伸展构造环境影响和作用下，北京平原区内隐伏着的北东向引张性正断活动，形成了“两隆一凹”的构造格局[1]。其中黄庄—高丽营断裂为北京凹陷西界的主控断裂、南苑—通县断裂为北京凹陷与大兴隆起的分界。第四纪北京地区“两隆一凹”构造图式消失，出现南北段构造分异局面，北西向的南口—孙河断裂的活动对北京地区北段构造变异起重要作用。由于该枢纽断裂(其北西段东北盘上升，西南盘下降；其东南段东北盘下降，西南盘上升)强烈活动，致使京西隆起和北京凹陷发生重点分异[2]。

南口—孙河断裂是北京地区规模最大的一条北西向断裂，总体呈320°～330°方向展布，其北西端起自昌平南口镇，向南东方向经百泉、孙河，长约50 km。断裂北西段(南口至北七家段)倾向SW，形成一个NW向的陷落带，控制北西向马池口第四纪凹陷，凹陷内第四系厚达600多米。断裂南东段(北七家至孙河段)倾向NE，与黄庄—高丽营断裂北段共同控制了顺义凹陷。20世纪70年代末，北京地震地质会战期间布设的钻孔及地球物理勘测，证实该断裂带在第四纪时期存在强烈活动[3]； 2001年江娃利等在昌平旧县村开挖探槽对南口—孙河断裂的古地震事件进行分析，并得出该断裂是北京地区未来发生强震的构造区域[4]；中国地震局曾在该断裂北西段的雪山村、旧县村和百泉庄等地区做了大量的研究工作，取得了该断裂北西段的展布及活动性的详细资料[5-10]；2014年张磊等通过对南口—孙河断裂北西段物探、钻探及槽探工作的分析，对该断裂进行精细定位，并对该段第四纪以来的活动规律进行探讨[11-12]；通过对该断裂南段钻孔分析，结合磁性地层测年数据，分析了该断裂南段的活动规律[13]。

地球轨道参数的周期性变化引起了地球表面日照量的周期性变化，进而导致全球气候的周期性变化[14-18]。气候的周期性变化记录在对气候变化响应敏感的沉积系统中，如沉积物结构、构造、岩性、岩相以及能够反映古气候变化的替代性指标的旋回性变化[19-25]。不同地质历史时期，地球轨道参数具有相对稳定的周期，一旦从地层中识别出米兰科维奇旋回，就有可能建立分辨率达0.02～0.04 Ma 的天文年代标尺[26]。因此，记录在沉积地层中的地球轨道信号能够成为强有力的测年工具，并可用于建立高分辨率的天文地质年代表(ATS)。旋回地层学的开展和应用，提高了地层年代框架的精度和分辨率，可以实现对整个第四纪时期断裂活动规律的探讨，对深入认识断裂的活动性具有重要意义。

本文以北京平原南口—孙河断裂南段上、下两盘钻孔磁性地层研究获得的第四纪年代格架为时间锚点，利用钻孔的沉积物磁化率、自然伽马测试数据进行旋回地层分析，建立了精度为0.1 Ma的连续天文年代标尺。通过对比断层两盘不同地质时期的地层沉积速率，实现了对南口—孙河断裂第四纪以来活动规律精细探讨的目的，并结合中国大陆新构造运动特点对其构造意义进行了探讨。

1 初始年代框架

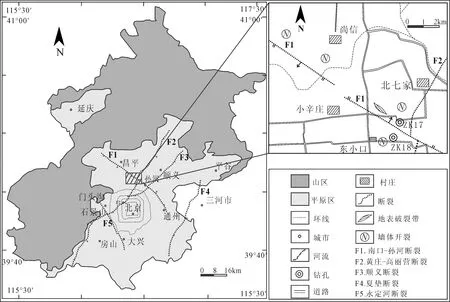
图1 北京平原主要活动断裂分布及钻孔位置图Fig.1 Distribution of main active faults in Beijing plain and the location of drillholes

初步的年代学框架(生物地层学、磁性地层学、放射性同位素年代学等)是取得良好旋回地层学研究成果的保证，即使年代框架具有较大误差范围，它也能够让研究者大致估计出平均沉积速率，为判别旋回地层学分析的合理性提供独立的证据[17-18]。

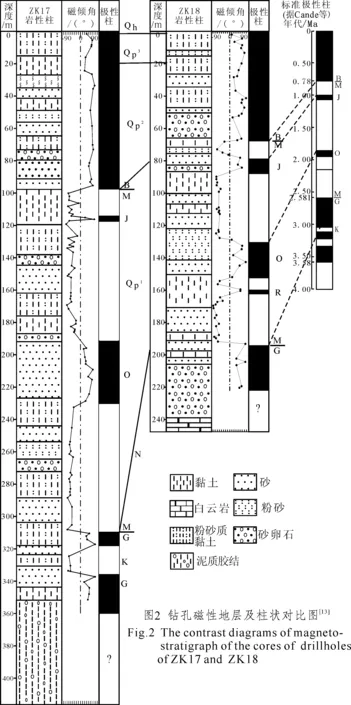
本次工作在南口—孙河断裂南段共布设了2个钻孔(图1)，其中ZK17地理坐标为116°25′40″E、40°5′51″N，孔深416.6 m，其构造位置属于南口—孙河断裂的上盘；ZK18孔地理坐标为116°25′32″E、40°5′16″N，孔深247.6 m，其构造位置属于断裂的下盘。钻探工程采用油压式钻机，全孔取心率达90%以上，岩心直径90 mm。取心率和岩心状况满足磁性地层学研究及高分辨率测试的要求。钻孔剖面的磁性地层学研究和钻孔岩性沉积相分析为旋回地层学分析提供了初始的年代格架[12](图2)。钻孔ZK17第四系下更新统(M/G界线)、中更新统(B/M界线)、上更新统和全新统底界分别为309 m、98 m、25.7 m和1.0 m；ZK17的磁性地层Jaramilo底界为118 m，Olduvai底界为230 m。钻孔ZK18下更新统底界为192.5 m ,中更新统界线深度为68 m，上更新统底界为21.6 m，全新统底界为0.8 m；ZK18的磁性地层Jaramilo底界为87 m，Olduvai底界为153 m。

2 旋回地层学分析

诸多用于旋回地层学分析的古气候替代指标中，磁化率和测井曲线(尤其是自然伽马曲线)是进行旋回分析的理想目标[27-28]。国内外已有很多学者利用这些替代指标成功进行了旋回地层学的分析和研究[26-37]。

工作区的钻孔ZK17的自然伽马测井数据和ZK18的磁化率数据均显示出了很好的旋回性，适合开展旋回地层学分析。分析前先对数据进行去线性趋势、去均值和归一化预处理，利用SSA-MTM谱分析软件包进行频谱分析[38]，采用Analyseries 2.0.4软件[39]进行滤波处理和天文调谐。

2.1 钻孔ZK17旋回地层学分析

ZK17孔自然伽马数据的频谱分析结果揭示出明显的旋回性(图3(a))，具有58.5 m，27.3 m，21.0 m，18.6 m，15.7 m，11.7 m，9.4 m，7.8 m，6.6 m，5.7 m，5.2 m，4.9 m，4.3 m，4.0 m，3.8 m，3.4 m，3.0 m的主周期，其中(27.3～15.7 m)∶(11.7～6.6 m)∶(5.7～3 m)的比值接近5∶2∶1，与短偏心率100 ka∶斜率40 ka∶岁差20 ka的比值接近，这些旋回可能分别代表了短偏心率、斜率和岁差沉积旋回。根据初始年代格架，将自然伽马数据在深度域上的变化转换为时间域上的变化后(图3(b))，频谱分析结果显示出明显的短偏心率、斜率和岁差周期(图3(c))。对初始年代格架下的自然伽马序列进行100 ka的短偏心率信号滤波处理(图4(c))，以磁性倒转年龄为锚点，参考滤波曲线，将自然伽马序列对比到理论偏心率曲线上[40]；其依据是将自然伽马高值对比到偏心率高值上，低值对比到偏心率低值上，据此建立了ZK17孔的天文年代标尺(图4(c)和(d))。根据新建立的天文年代标尺，确定出该井的沉积速率在9～33 cm/ka之间变化(图4(e))。对经过调谐后的数据再进行频谱分析，揭示出409 ka,95 ka,47 ka,20 ka,23 ka的主周期，与天文理论周期更为接近，表明ZK17孔的沉积过程受到地球轨道参数引起的古气候变化的控制(图4(c))。

2.2 钻孔ZK18旋回地层学分析

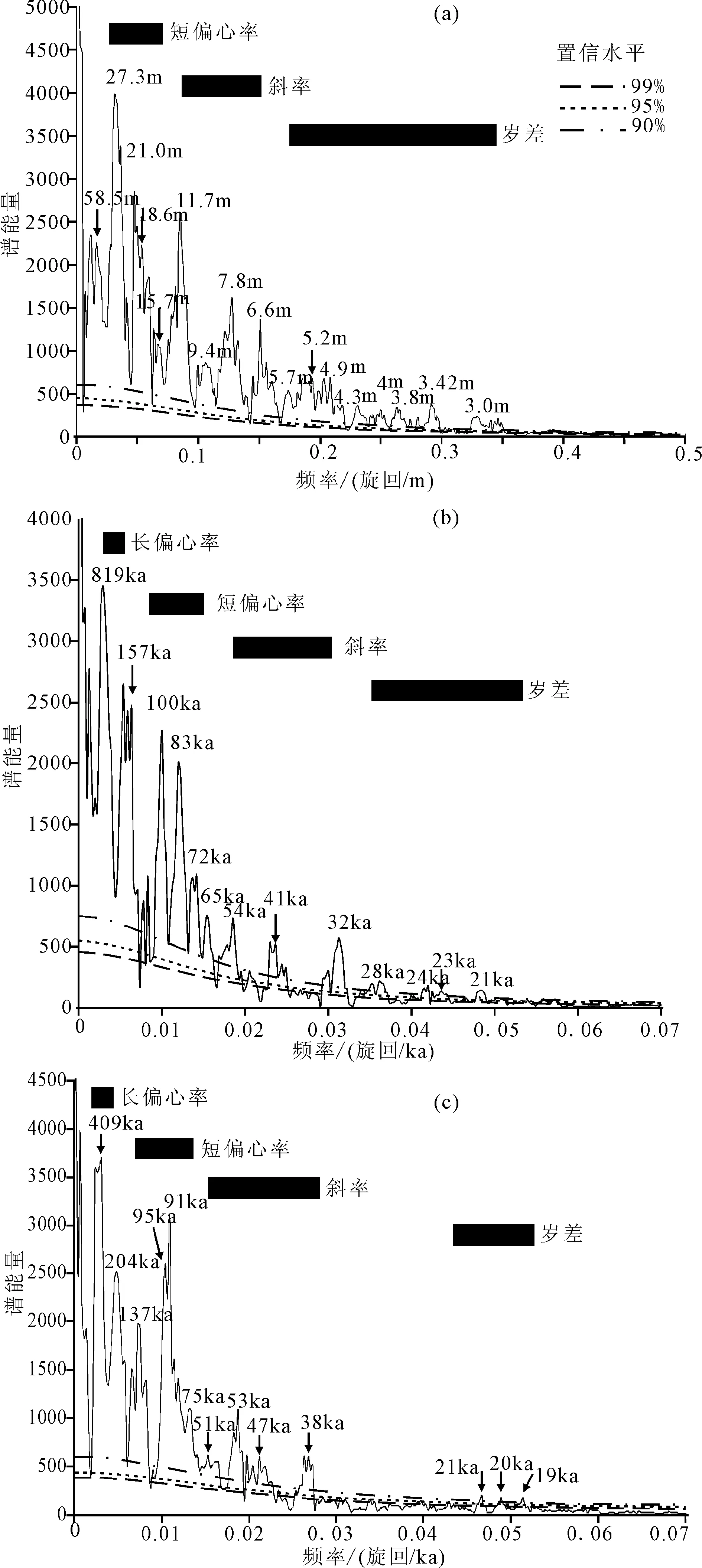
图3 ZK17孔自然伽马在深度域(a)、初始年代格架(b)和调谐后(c)频谱分析结果Fig.3 Natural gamma ray data with depth and the preliminary age framework,and after tuning in drillhole ZK17

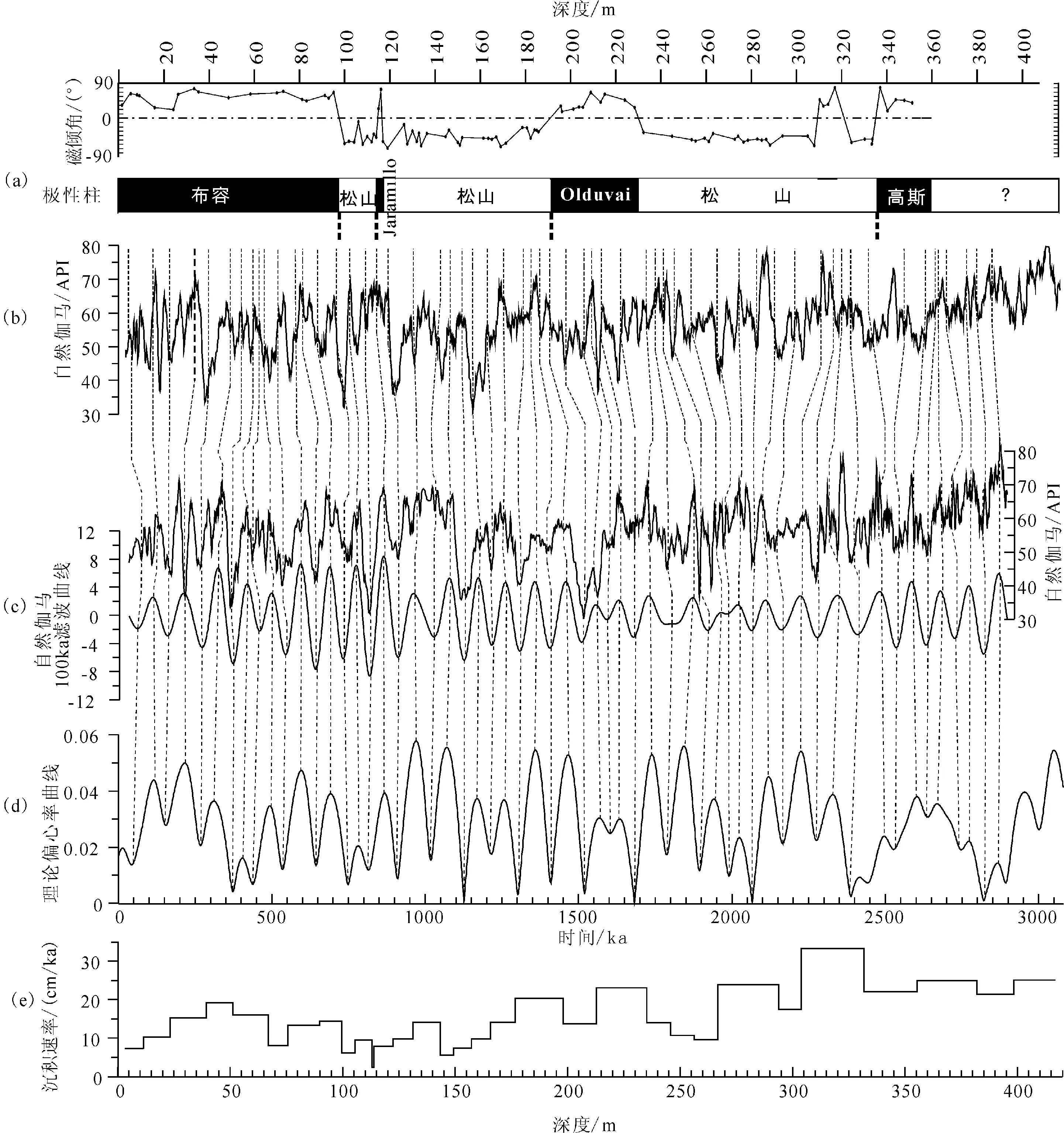
图4 ZK17孔天文年代标尺Fig.4 The astronomical age reference of continuous stratigraphic formations in drillhole ZK17(a)磁倾角与地磁极性柱；(b) 自然伽马在深度域上的变化特征；(c) 理论偏心率曲线[37]；(d) 根据古地磁极性柱提供的初始年代格架将自然伽马在深度域上的变化转化为时间域，并获得100 ka的滤波曲线；(e) 根据天文调谐结果确定的沉积速率

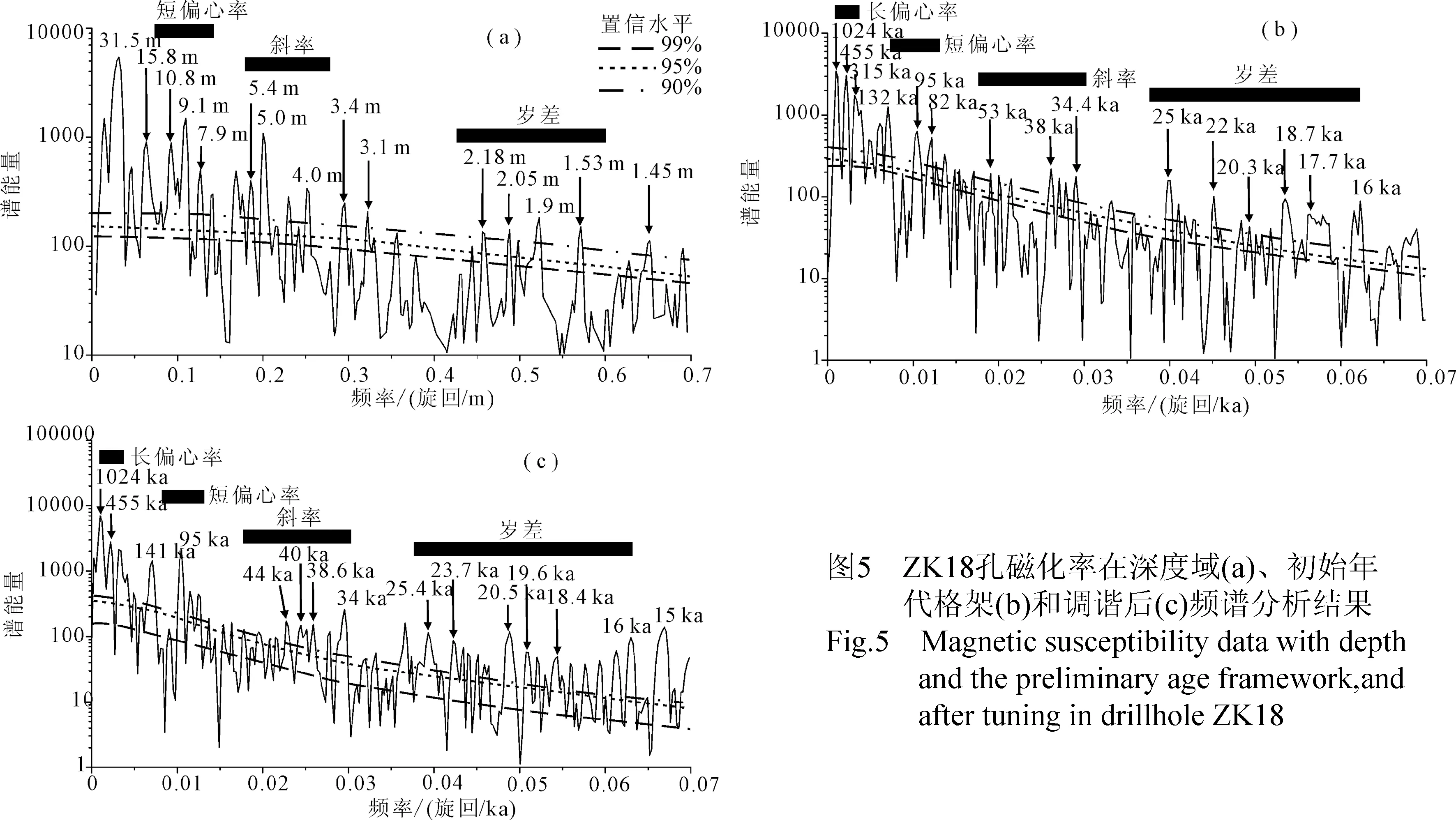
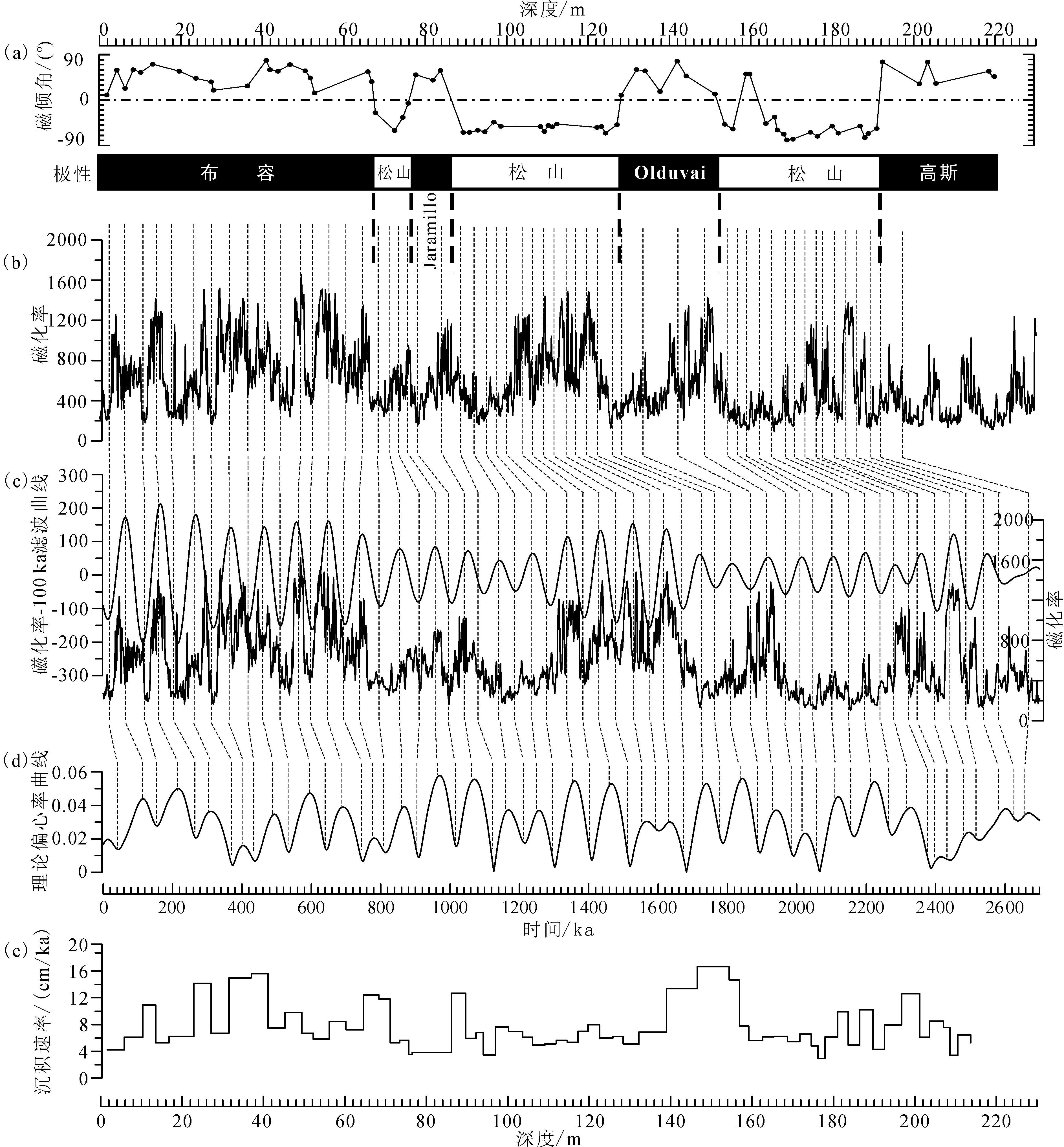
图6 ZK18孔天文年代标尺Fig.6 The astronomical age reference of continuous stratigraphic formations in drillhole ZK18(a)磁倾角与地磁极性柱；(b) 磁化率在深度域上的变化特征；(c) 根据古地磁极性柱提供的初始年代格架将磁化率在深度域上的变化转化为时间域，并获得100 ka的滤波曲线; (d) 偏心率理论曲线[37]及其与磁化率曲线的对比；(d)理论偏心率曲线；(e) 根据天文调谐结果确定的沉积速率

ZK18孔磁化率数据的频谱分析结果揭示出明显的旋回性(图5(a))，具有31.5 m,15.8 m,10.8 m,9.1 m,7.9 m,5.4 m,5.0 m,4.0 m,3.4 m,3.1 m,2.18 m,2.05 m,1.9 m,1.53 m和1.45 m的主周期，其中(13～7.9 m)∶(5.4～3.4 m)∶(2.2～1.4 m)的比值接近5∶2∶1，与短偏心率100 ka∶斜率40 ka∶岁差20 ka的比值接近，这些旋回可能分别代表了短偏心率、斜率和岁差沉积旋回。根据磁性地层学结果及第四纪年代格架建立的初始年代格架，将磁化率数据在深度域上的变化转换为时间域上的变化后(图5(b))，频谱分析结果显示出明显的短偏心率、斜率和岁差周期(图5(c))。对初始年代格架下的磁化率序列进行100 ka的短偏心率信号滤波处理(图6(c))，以磁性倒转年龄及第四纪年代为锚点，参考滤波曲线，将磁化率序列对比到理论偏心率曲线上，其依据是将磁化率高值对比到偏心率高值上，磁化率低值对比到偏心率低值上，据此建立了ZK18孔的天文年代标尺(图6(c)和(d))。根据新建立的天文年代标尺，确定出该井的沉积速率在4～18 cm/ka之间变化(图6(e))。对经过调谐后的数据再进行频谱分析，揭示出455 ka,95 ka,40 ka,23.7 ka,19.6 ka和16 ka的主周期，与天文理论周期更为接近，表明ZK18孔的沉积过程受到地球轨道参数引起的古气候变化的控制，也表明北京平原地区的气候变化受到地球轨道力的影响(图6(c))。

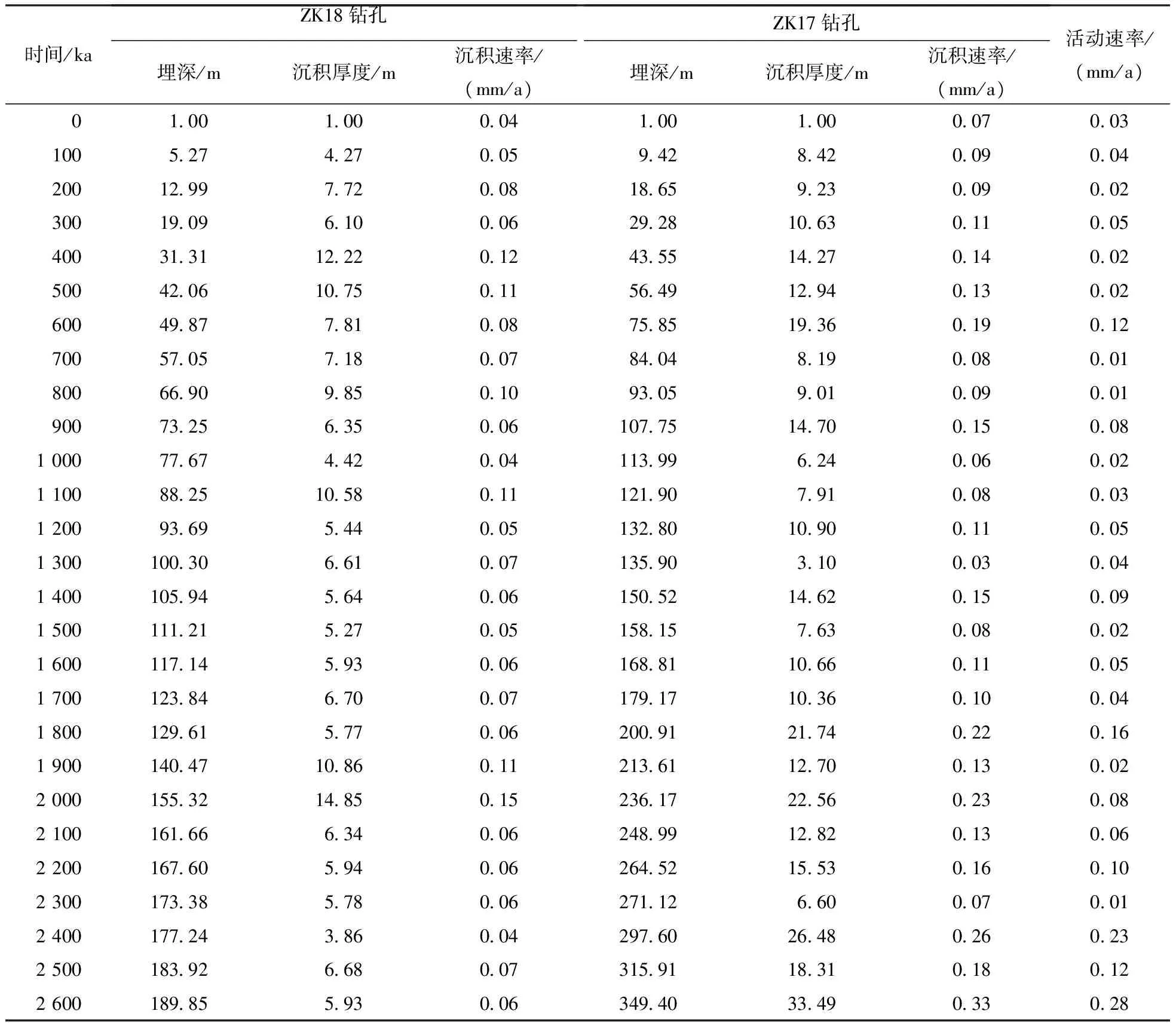
表1 南口—孙河断裂每100 ka活动速率统计Table 1 Active rates per 100 ka in Nankou-Shunhe fault zone

3 南口—孙河断裂活动规律及其构造意义

位于断裂两盘的钻孔第四纪以来不同时间段内的地层岩性、沉积厚度或者堆积速率是具有明显差异的，具体表现为,上盘较下盘同时代的沉积物具有厚度增大、细粒沉积物层数增多和堆积速率增高等地层学特征，它们客观地记录了该断裂两侧垂直差异运动的过程。假定断裂无蠕滑现象的话，断裂两侧的垂直差异运动是通过粘滑错动实现的。

根据旋回分析建立的钻孔ZK17和ZK18的天文年代标尺，以0.1 Ma作为时间间隔，计算断裂两盘钻孔的地层落差及沉积速率差(表1)，从而得到该断裂第四纪以来活动强度的变化特征曲线(图7)。南口—孙河断裂第四纪以来可以识别出6个相对较强的活动幕。

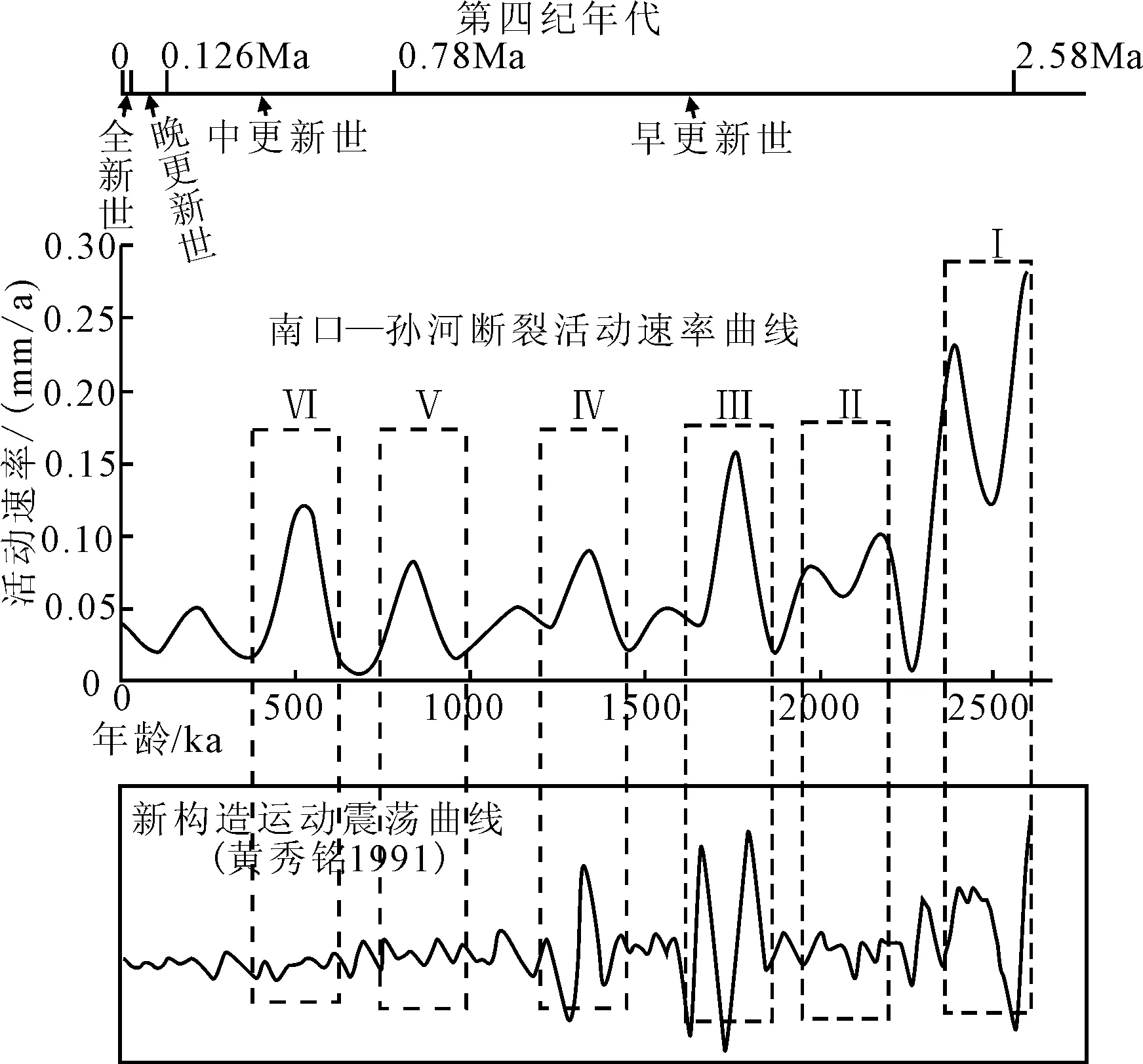
图7 第四纪以来南口—孙河断裂的活动速率曲线Fig.7 Curves showing active rates of Nankou-Sunhe fault since Quaternary

早更新世时期，南口—孙河断裂活动强烈，存在4个明显的活动幕(Ⅰ—Ⅳ幕)，且具有明显的间歇性活动特点，对于其中Ⅰ幕(2.4～2.6 Ma)、Ⅲ幕(1.8 Ma)，活动较为显著，平均活动速率分别为0.21 mm/a和0.16 mm/a；Ⅱ幕(2.0～2.2 Ma)、Ⅳ幕(1.4 Ma)活动强度相对较弱，平均活动速率为0.08 mm/a和0.09 mm/a。1991年，黄秀铭等学者对北京西山地区的夷平面特征进行研究，编绘了北京地区与新构造运动震荡曲线，同样识别出了上述4个活动周期[1](图7)。笔者认为，南口—孙河断裂能够较好地表征本区新构造运动的特点，其第Ⅰ幕和第Ⅲ幕分别对应了青藏高原隆升的两次主幕，即青藏运动的B幕(2.6 Ma)和C幕(1.7 Ma)[40]。早更新世断裂活动强弱间隔为0.4 Ma，表明北京地区同样具有0.4 Ma准周期的新构造运动特点。

中更新世时期，南口—孙河断裂具有继承性活动的特点，活动强度较早更新世有所减弱，存在2个明显的活动幕(Ⅴ幕和Ⅵ幕)。Ⅴ幕(0.9 Ma)平均活动速率为0.08 mm/a，Ⅵ幕(0.6 Ma)平均活动速率为0.12 mm/a。而发生于早更新世晚期(1.2～0.6 Ma B.P.) 的构造运动,是中国大陆地区一次十分强烈的构造运动，构造上被称为“昆黄运动”。这次事件亦造成了全球气候及环境的显著变化[40-42]。

晚更新世时期，南口—孙河断裂的平均活动速率为0.03 mm/a,活动性较之前减弱；全新世以来，从活动速率曲线看，有增强的趋势，这一点与张磊等[13]的研究结果一致。

4 结 论

通过对北京平原南口—孙河断裂上、下两盘钻孔第四纪沉积地层的磁化率和测井曲线进行旋回地层学研究，建立了精度为0.1 Ma的连续天文年代标尺，对比断层两盘不同地质时期的地层垂直落差，分析了南口—孙河断裂第四纪以来的活动规律，获得了以下两点认识。

(1)磁化率和测井数据可以较好地反映陆相地层沉积物粒度的差异，以磁性地层测年结果为时间锚点，进行旋回地层分析，可以实现第四纪地层高精度地层对比的目标。

(2)基于旋回地层年代学的研究成果分析，北京平原南口—孙河断裂第四纪以来具有间歇性活动的特征，可识别出6个相对较强的活动幕。其中早更新世存在4个明显的活动幕，活动周期具有0.4 Ma准周期的特点，第Ⅰ幕和第Ⅲ幕分别对应了青藏高原隆升期的青藏运动的B幕(2.6 Ma)和C幕(1.7 Ma)，中更新世的活动特征则对应了“昆黄运动”，北京地区新构造运动特征与之有较好的呼应关系。

参考文献：

[1] 黄秀铭，汪良谋，徐杰，等.北京地区新构造运动特征[J] .地震地质，1991，13(1)：43-51.

[2] 焦青，邱泽华.北京平原地区主要活动断裂带研究进展[J] .地壳构造与地壳应力文集，2006(1)：72-84.

[3] 邓启东，徐锡伟，张先康，等.城市活动断裂探测的方法和技术[J].地学前缘，2003，10(1)：601-605.

[4] 江娃利，侯治华，谢新生.北京平原南口—孙河断裂带昌平旧县探槽古地震事件研究[J] .中国科学(D辑)，2001，31(6)：501-509.

[5] 张世民，王丹丹，刘旭东，等.北京南口—孙河断裂带北段晚第四纪活动的层序地层学研究[J].地震地质，2007，29(4)：729-743.

[6] 张世民，王丹丹，刘旭东，等.北京南口—孙河断裂晚第四纪古地震事件的钻孔剖面对比与分析[J].中国科学(D辑)，2008，38(7)：881-895.

[7] 向宏发，方仲景，张晚霞，等.北京平原区隐伏断裂晚第四纪活动特征的联合剖面研究[J].地震研究，1996，18(1)：75-79.

[8] 侯治华，钟南才，郝彦军，等.应用高密度电法探测北京南口—孙河隐伏断裂[J] .防灾科技学院学报，2011，13(4)：1-6.

[9] 车兆宏.南口—孙河断层活动性研究[J] .地震地质，1994，16(2)：115-120.

[10] 向宏发，方仲景，贾三发，等.隐伏断裂研究及其工程应用——以北京平原区为例[M] .北京:地震出版社，1994:1-97.

[11] 张磊，白凌燕，蔡向民，等.北京平原南口—孙河断裂带北西段活动性分析[J].中国地质， 2014， 41(3)：902-911.

[12] 张磊，白凌燕，蔡向民，等.北京南口—孙河断裂北西段综合物探剖面定位及其活动性研究[J].现代地质，2014，28(1)：234-242.

[13] 张磊，白凌燕，蔡向民，等.北京平原南口—孙河断裂南段第四纪活动性的磁性地层学研究[J].第四纪研究， 2014， 34(2)：1-10.

[14] 徐道一.天文地质年代表与旋回地层学研究进展[J].地层学杂志， 2005，29(增刊)：635-640.

[15] 徐道一，韩延本，李国辉，等.天文地层学的兴起[J].地层学杂志， 2006， 30(4)：323-326.

[16] 汪品先.地质计时的天文“钟摆”[J].海洋地质与第四纪地质， 2006，26(1)：1-7.

[17] HINNOV L A，OGG J G.Cyclostratigraphy and the astronomical time scale[J].Stratigraphy， 2007，4:239-251.

[18] 吴怀春，张世红，冯庆来，等.旋回地层学理论基础、研究进展和展望[J].地球科学——中国地质大学学报，2011，36(3)：409-428.

[19] 吴怀春，张世红，黄清华，等.中国东北松辽盆地晚白垩世青山口组浮动天文年代标尺的建立[J].地学前缘，2008，15(4)：159-169.

[20] 刘洋，吴怀春，张世红，等.珠江口盆地珠一坳陷韩江组—万山组旋回地层学[J].地球科学——中国地质大学学报，2012，37(3)：411-423.

[21] 姚益民，付国斌，徐道一，等.新疆吐哈盆地侏罗系旋回地层的初步研究[J].地层学杂志，2003，27(2)： 122-128.

[22] 程日辉，王国栋，王璞珺，等.松科1井南孔白垩系青山口组一段沉积序列精细描述：岩石地层、沉积相与旋回地层[J].地学前缘，2009，16(2)：314-323.

[23] 张磊，何付兵，白凌燕，等.北京顺义断裂北段第四纪活动的天文旋回地层学研究[J].中山大学学报(自然科学版)，2015，54(5)：147-154.

[24] 贾鹏，李伟，卢远征，等.四川盆地中南部地区洗象池群沉积旋回的碳氧同位素特征及地质意义[J].现代地质，2016，30(6)：1329-1338.

[25] 孙阳，樊太亮，傅良同，等.大庆长垣姚家组高频层序地层与米兰科维奇旋回对应性[J].现代地质，2011，25(6)：1145-1151.

[26] WU H C，ZHANG S H，JIANG G Q，et al.The floating astronomical time scale for the terrestrial Late Creteaceous Qingshankou Formation from the Songliao Basin of Northeast China and its stratigraphic and paleoclimate implications[J].Earth and Planetary Science Letters，2009，278:308-323.

[27] 徐道一，姚益民，韩延本，等.山东东营凹陷新宾系明化镇组天文地层研究[J].古地理学报，2008，10(6)：287-296.

[28] PROKOPH A， VILLENEUVE M， AGTERBERG F P.Geochronology and calibration of global Milankovitch cyclicity at the Cenomanian Turonian boundary[J].Geology，2001，29(6):523-526.

[29] 龚一鸣，杜远生，童金南，等.旋回地层学：地层学解读时间的第三里程碑[J].地球科学——中国地质大学学报，2008，33(4)：443-457.

[30] 姚益民，徐道一，张海峰，等.陆相沉积的天文地层研究方法简介——以井下地层为例[J].地层学杂志，2007，31(增刊)： 431-442.

[31] 侯红明，汤贤赞，王保贵，等.南沙群岛海域沉积物古地磁参数对米兰科维奇周期的响应[J] .热带海洋，1995 (3)：1-7.

[32] 田军，汪品先，成鑫荣，等.南海ODP1143站上新世至更新世天文年代标尺的建立[J].地球科学——中国地质大学学报， 2005，30(1)：31-39.

[33] 田军，汪品先，成鑫荣，等.南海ODP1148站中中新世(12～18.3Ma)天文调谐的年代标尺[J].地球科学——中国地质大学学报，2005,30(5)：513-518.

[34] TEN VEEN J H ，GEORGE P.Astronomically forced variations in gamma-ray intensity: Late Miocene hemipelagic successions in the eastern Mediterranean basin as a test case[J].Geology，1996，24(1):15-18.

[35] PROKOPH A， VILLENEUVE M， AGTERBERG F P.Geochronology and calibration—Turonian boundary[J].Geology，2001，29(6):523-526.

[36] WEEDON G P，COE A L， GALLOIS R W,et al.Cycolstratigraphy， orbital tuning and inferred productivity for the type Kimmeridge Clay (Late Jurassic)，southern England[J].Journal of the Geological Society，2004，161(4):655-666.

[37] WU H C，ZHANG S H，HUANG Q H.Establishment of floating astronomical time scale for the terrestrial Late Cretaceous Qing-shankou Formation in the Songliao basin of Northeast China[J].Earth Science Frontiers，2008，15(4): 159-169.

[38] GHIL M，ALLEN M R，DETTINGER M D,et al.Advanced spectral methods for climatic time series[J].Review of Geophysics，2002，40(1)：1-3.

[39] PAILLARD D， LABEYRIE L，YIOU P.Macintoshi program performs time-series analysis[J].Eos，1996，77:379.

[40] LASKAR J，ROBUTE l P，JOUTE L F,et al.A long-term numerical solution for the insolation quantities of the Earth[J].Astronomy and Astrophysics，2004，28: 261-285.

[41] 李吉均，方小敏，潘保田，等.新生代晚期青藏高原强烈隆起及其对周边环境的影响[J].第四纪研究，2001，21(5)：381-391.

[42] 朱照宇，王俊达，张国梅，等.华南沿海B/M界线附近的群发地质事件[J] .海洋地质与第四纪地质，1993，13(3)：35-42.

[43] 朱照宇.具有0.4 Ma准周期的事件群发性与气候-构造旋回刍论——以黄土区为对比区[J] .地球化学，1994，23(1)：69-79.