一种强干扰条件下阵列天线波达方向估计方法

宫 健， 楼顺天， 张伟涛

(1. 西安电子科技大学 电子工程学院，陕西 西安 710071；2. 空军工程大学 防空反导学院，陕西 西安 710051)

一种强干扰条件下阵列天线波达方向估计方法

宫 健1,2， 楼顺天1， 张伟涛1

(1. 西安电子科技大学 电子工程学院，陕西 西安 710071；2. 空军工程大学 防空反导学院，陕西 西安 710051)

为解决强干扰条件下阵列天线的波达方向估计问题，定义了保向正交性和特征波束的概念，证明了信源同时满足功率差和角度差较大条件时，所对应的特征矢量具有保向正交性，提出了一种基于干扰特征矢量剔除的波达方向估计算法．最后，通过计算机仿真，验证了所提算法在强干扰条件下比干扰阻塞算法有更高的估计性能．

阵列天线;电子干扰;波达方向估计;信号处理

阵列天线在雷达、声纳、通信等军事领域具有重要的应用价值[1-4]．在阵列信号处理中，一般认为信源所对应的矩阵特征矢量和其对应的阵列导向矢量间没有特定关系[5-7]．一直以来存在这种认识误区的主要原因是忽略了信源功率因素的影响[8-9]．文中围绕信源功率，首先定义了保向正交性和特征波束的概念，从理论上推导了两个信源的保向正交性条件；在此基础上，分析讨论了更为普遍的多个信源的保向正交性条件，并将这一理论用于解决强干扰背景下阵列天线的波达方向(Directional Of Arrival，DOA)估计．

当干扰源功率超出信源功率较大时，谱估计时干扰伪峰会大于信源的谱峰，不利于对信源的检测与定位．目前解决此类问题的方法主要有松弛算法[10]、清除算法[11]等．然而这些算法每一步估计都需要通过迭代来实现，运算量相当大，很难实际应用．另外，文献[12]中提出了较为实用的干扰阻塞算法(Jamming Jam Method，JJM)，可通过构造阻塞矩阵来抑制干扰，但是需要事先知道干扰的方位，而实际中干扰方位往往无法预知．为此，笔者提出了一种基于信源保向正交性的干扰特征矢量剔除算法，该算法在强干扰条件下比现有算法有着更高的角度估计性能，并且不需事先知道干扰源的角度．

1 信源保向正交性相关定义

1.1 保向正交性定义

1.2 特征波束定义

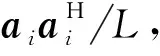
(1)

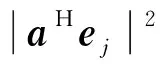
2 强弱信源保向正交条件推导

2.1 强弱信源功率相差不大

根据文献[13]，两个信源接收协方差矩阵的大特征值及其特征向量满足:

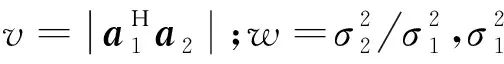
(4)

根据参考文献[14]，可推导出:

(5)

这表明在等功率情况下，信源特征矢量既不保向也不正交．

2.2 强弱信源功率相差极大

随着信号功率差别的增大，在极限情况即w→0时，由洛必达法则有

式(7)和式(8)表明，在w→0，即信源功率相差较大时，特征向量e1具有保向性但并不与a2正交，除非v=0; 特征向量e2与a1正交，是否具有保向性则需要进一步分析．

为简化问题，将噪声略去，对数据协方差矩阵进行分解，有下式成立:

(9)

当w→0时，有

(10)

若同时满足式(9)条件，可以推得

(11)

其中，δ为使e2满足规范化条件的任意矢量．而从满足式(8)的条件出发，可以推得

(12)

也就是说，当信源2和信源1的功率相差很大时，比如通常会遇到的信源1位于天线波束主瓣而信源2位于天线波束旁瓣的情况，e2仍具有保向特性．

2.3 信源保向正交性条件

根据上面的推导可知，即使v≠0，在两信源功率相差很大的前提条件下，信源特征矢量仍具有保向正交特性．只是此时的正交特性修改为弱信源对应特征向量向强信源的导向矢量正交．同时，在两信源功率相等到功率差逐渐增大的过程中，这种性质会从无到有，从不明显到明显．同理，这一结论可推广至多个信源的情况．所以，可通过剔除掉强干扰源对应的特征矢量来抑制干扰，这也正是文中所提DOA算法的理论基础．

3 强干扰背景弱信源DOA估计算法

3.1 算法的基本原理

假设信源总数为M，其中干扰源的个数为J，当其功率满足

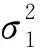
时, 可以推导出

σ1α>σ2α>…>σJα≫σJ+1α>…>σMα,

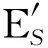
在实际处理中，可按照相邻特征值变化情况来确定干扰对应的大特征值个数J，即

λJ/λJ+1≫λJ+1/λJ+2．

(13)

(14)

根据多重信号分类法，可以求解出信源的DOA为

(15)

3.2 算法的基本步骤

文中算法的基本步骤如下：

步骤5 利用式(15)，实现对目标信号源DOA的估计．

4 计算机仿真结果

假设雷达天线为等间距均匀线阵，阵元数为16，阵元间距d=λ/2，λ为工作波长，采样点数为200．当为转发式干扰时，干扰源和目标源的信号具有相干性，仿真时在步骤2之前采用Toeplitz矩阵重构法[15]对数据解相干，取空间噪声为高斯白噪声．

4.1 干扰源和目标源的保向正交性

假设干扰源位于0°，目标源角度从0°到90°按步长1°变化，信噪比为 10 dB，干信比从 0 dB 按步长 1 dB 变化到 90 dB．对信源功率和角度间隔变化时，特征向量到导向矢量的投影情况如图1所示．

图1 特征矢量到导向矢量投影随角度间隔及干信比变化

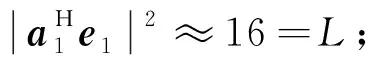
4.2 文中算法与JJM算法性能比较

假设干扰源个数为1，角度位于0°，干信比为50 dB，分别仿真2个和3个目标源且信噪比不同时的空间谱．图2(a)为2个目标源的仿真，角度分别为 -10° 和 -20°，信噪比分别为 0 dB 和 10 dB，图2(b)为3个目标源的仿真，角度分别为 -20°、-10° 和30°，信噪比分别为 0 dB、5 dB 和 10 dB．

由仿真可见，在干信比为50 dB的强干扰条件下，所提算法可以准确地对目标源进行DOA估计， 而JJM算法在这种情况下完全失效．

5 结 束 语

文中从理论上证明了信源同时满足功率差和角度差较大条件时，所对应的特征矢量具有保向正交性．针对强干扰背景下目标的波达方向估计问题，笔者提出了一种基于干扰特征矢量剔除的算法．最后，通过仿真实验说明了该算法比JJM算法有着更高的角度估计性能，其成果在灵巧干扰等复杂电磁环境下的实际应用有待进一步研究．

参考文献：

[1] RABBANI M S, GHAFOURI-SHIRAZ H. Liquid Crystalline Polymer Substrate-based THz Microstrip Antenna Arrays for Medical Applications[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 1533-1536.

[2] TANHA M A, BRENNAN P V, ASH M, et al. Overlapped Phased Array Antenna for Avalanche Radar[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(8): 4017-4026.

[3] ZHANG G, ZHANG Q F, CHEN Y F, et al. Dispersive Feeding Network for Arbitrary Frequency Beam Scanning in Array Antennas[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(6): 3033-3040.

[4] ZHANG H Y, ZHANG F S, ZHANG F, et al. High-power Array Antenna Based on Phase-adjustable Array Element for Wireless Power Transmission[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 2249-2253.

[5] SHI J P, HU G P, ZONG B F, et al. DOA Estimation Using Multipath Echo Power for MIMO Radar in Low-Grazing Angle[J]. IEEE Sensors Journal, 2016, 16(15): 6087-6094.

[6] SHI J P, HU G P, LEI T. DOA Estimation Algorithms for Low-angle Targets with MIMO Radar[J]. Electronics Letters, 2016, 52(8): 652-654.

[7] HASSANIEN A, VOROBYOV S A V, KHABBAZIBASMENJ A. Transmit Radiation Pattern Invariance in MIMO Radar with Application to DOA Estimation[J]. IEEE Signal Processing Letters, 2015, 22(10): 1609-1613.

[8] DEWANTARI A, KIM J, JEON S Y, et al. Gain and Side-lobe Improvement of W-band Microstrip Array Antenna with CSRR for Radar Applications[J]. Electronics Letters, 2017, 53(11): 702-704.

[9] GONG Y H, WANG R B, WANG P. Improved Phase-encoding Calibration for Active Phased-array Antennas of SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(6): 767-771.

[10] 董文益. 强干扰条件下弱信号DOA估计算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.

[11] 王璐, 李素姣, 张耀天, 等. 利用周期重复CLEAN的GNSS欺骗式干扰抑制算法[J]. 信号处理, 2015, 31(12): 1636-1641.

WANG Lu, LI Sujiao, ZHANG Yaotian, et al. Spoofing Interference Suppression in GNSS Using Repeated CLEAN[J]. Journal of Signal Processing, 2015, 31(12): 1636-1641.

[12] 高阳, 许稼, 龙腾. 阻塞矩阵抗干扰方法性能分析[J]. 信号处理, 2015, 31(10): 1361-1365.

GAO Yang, XU Jia, LONG Teng. Performance Analysis of Anti-jamming Method via Block Matrix[J]. Journal of Signal Processing, 2015, 31(10):1361-1365.

[13] SCHMIDT R O. Multiple Emitter Location and Signal Parameter Estimations[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280.

[14] 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004: 167-192.

[15] 司伟建, 吴迪, 韩惠莲. 基于相关Toeplitz预处理的二维测向方法[J]. 中南大学学报:自然科学版, 2015, 46(8): 2892-2897.

SI Weijian,WU Di, HAN Huilian. 2-D Direction Finding Method Based on Correlation Toeplitz Pretreatment[J]. Journal of Central South University: Science and Technology, 2015, 46(8): 2892-2897.

MethodofarrayantennaDOAunderstronginterferencepresence

GONGJian1,2，LOUShuntian1，ZHANGWeitao1

(1. School of Electronic Engineering, Xidian Univ., Xi’an 710071, China；2. Air Force Engineering Univ., Xi’an 710051, China)

In order to solve the problem of DOA estimation for the array antenna under strong interference,the concept of preserving orthogonality and characteristic beam is defined. It is proved theoretically that the characteristic vector of the corresponding feature vector is guaranteed when the source power and the angle interval are both large. And a novel DOA estimation algorithm based on the interference source feature vector is proposed. Through the simulation and comparison of JJM algorithm it is shown that the proposed algorithm has a better statistical estimation performance than the JJM algorithm.

array antenna; electronic interference; direction of arrival; signal processing

2017-03-03

国家自然科学基金资助项目(61571339, 61501501)；航空科学基金资助项目(20150196003, 20150196007)

宫 健(1984-)，男，讲师，西安电子科技大学博士研究生，E-mail：wcyls@163.com．

10.3969/j.issn.1001-2400.2018.01.030

TN974

A

1001-2400(2018)01-0168-05

(编辑： 齐淑娟)