高斯粗糙表面涂覆目标太赫兹散射特性

赵 华， 郭立新

(西安电子科技大学 物理与光电工程学院，陕西 西安 710071)

高斯粗糙表面涂覆目标太赫兹散射特性

赵 华， 郭立新

(西安电子科技大学 物理与光电工程学院，陕西 西安 710071)

采用基于基尔霍夫近似的物理光学方法，研究了具有高斯粗糙表面的涂覆目标太赫兹散射特性．基于高斯粗糙面建立表面粗糙圆锥和锥柱目标模型，根据入射波频率对模型进行剖分以满足物理光学的计算要求．根据菲涅尔反射系数得出表面电流，进而计算涂覆粗糙目标的雷达散射截面．对比分析了粗糙表面目标与光滑目标的散射结果，详细讨论了不同涂覆介质、不同涂层厚度、不同入射角度、不同频率以及不同粗糙度的粗糙表面圆锥目标和锥柱目标的太赫兹散射特性．计算结果表明，在太赫兹波段目标表面的粗糙度对散射有显著的影响．

高斯粗糙面;表面粗糙目标;太赫兹;物理光学

近年来随着雷达目标特性研究的深入，相对于微波频段雷达，太赫兹[1]雷达以其更高的空间分辨率和角分辨率具有更大的优势，受到了越来越多的重视．太赫兹频段相比于微波频段频率更高，更容易发射大带宽信号，具有更高的分辨率，太赫兹波段目标表面的细微结构、粗糙度等细节会显著影响其后向散射特性，实现更小尺寸目标的探测、更精确目标的运动与物理参数反演．太赫兹(THz)波段位于微波与红外波之间，其频率范围为 0.1～ 10.0 THz (1 THz= 1012Hz)，对应的波长为 30 μm～ 3 mm．太赫兹频段目标散射特性是太赫兹雷达探测和成像[2]应用的物理基础，同时也是太赫兹雷达系统进行链路设计、特征提取以及成像算法的重要依据．太赫兹频段目标散射特性研究可分为实验测量和数值计算两种手段．在实验测量上，文献[3]利用 1.56 THz 源在紧缩场中对粗糙表面圆柱体的目标散射特性进行了研究．文献[4]依据实验数据，通过拟合Drude模型，有效地描述了由微波段向太赫兹与远红外频段过渡过程中铝的电磁参数变化的连续性和一致性规律．文献[5]研制了太赫兹数字全息成像系统，该系统可以对太赫兹电磁波的振幅、相位、频率及偏振等全部光学信息的三维空间分布进行精确测量．文献[6-7]搭建了以 0.2 THz 返波管振荡器源、热释电探测器、小型自动旋转光学平台等组成的太赫兹波目标散射特性实验测试系统，并对粗糙铜面的散射特性等进行了研究．在数值计算领域，文献[8]对太赫兹波频段的金属目标体的远场目标特性计算进行了研究．文献[9]利用高频方法研究了太赫兹频段介质体近场散射特性．文献[10]研究了不同粗糙度的非均匀不稳定表面粗糙导体目标在太赫兹波段的散射特性．文献[11-12]基于基尔霍夫近似研究了介质粗糙目标在远红外和光波段的散射特性，并考虑了高斯光束的情况．文献[13]考虑粗糙度修正表面的散射系数，研究了涂覆目标的太赫兹散射特性．

文中区别于以往采用经验公式以粗糙度修正散射系数[13]的研究方法，把随机粗糙面的建模理念应用到太赫兹波段表面粗糙目标的建模中．首先利用蒙特卡罗方法模拟了高斯粗糙面近似代替实际复杂的粗糙面，对生成的随机粗糙面进行坐标变换，导入建模软件，建立具有粗糙表面的目标模型; 然后对粗糙目标按照入射波的频率进行剖分，满足物理光学近似要求．根据菲涅尔反射系数求得表面电流，进而计算涂覆粗糙目标的雷达散射截面．并针对不同入射角、不同频率、不同粗糙度、不同涂覆介质材料以及不同涂覆厚度的表面粗糙涂覆目标，分别进行了仿真和分析．

1 表面粗糙目标模型的建立

采用蒙特卡罗方法生成高斯随机粗糙面[14]，将粗糙面均离散为M×N份，离散间隔为Δx和Δy，则模拟粗糙面的尺寸为Lx×Ly，其中长度Lx=MΔx，宽度Ly=NΔy．每一点的x坐标可以表示为xm= -Lx/ 2+ (m- 0.5) Δx(m=1，2，…，M)，y坐标可以表示为yn= -Ly/ 2+ (n- 0.5) Δy(n=1，2，…，N)，对应的高度起伏可表示为

(1)

其中，

(2)

其中，N(0，1)表示均值为0的高斯分布随机数，S(kx，ky)表示粗糙面的谱函数．文中设定粗糙面为高斯粗糙面，此时谱函数可表示为

(3)

其中，δ表示高斯粗糙面的均方根高度，lx和ly表示相关长度．用随机生成的高斯粗糙面模型来模拟目标表面的粗糙度，通过随机粗糙面环境的建模方法来实现．对应图1，所生成的高斯随机粗糙面按照

(4)

进行坐标变换．锥面上任一点所在截面的半径r=RL(1+f(x，y))/La，其中，La表示建立的粗糙圆锥的母线，底面半径为R．导入Rhino软件建立粗糙圆锥目标如图1(c)所示．

图1 粗糙面转换为圆锥示意图

2 理论分析

假设平面波照射到目标上，由Stratton-Chu积分公式，目标远区散射场利用物理光学可表示为[15-16]

(5)

其中，k和Z0分别为自由空间的波数和本征阻抗，i和s分别为入射波和散射波的单位矢量，r为表面上一点的位置矢量，r= |r|，n为目标表面向外单位法矢量，E和H分别为边界上总的电场和总的磁场．

图2 涂覆目标散射示意图

这里d为涂覆介质层的厚度，N1=(μ0ε0)1/2，对应介质中的N2=(μrεr)1/2，cosθr= (1- sin2θi/ (μrεr))1/2，有关各参数含义可参见文献[17]．

涂覆目标雷达散射截面的计算公式为

(12)

其中,

3 计算结果与分析

图3(a)给出了3 GHz平面波入射下涂覆半球的双站雷达散射截面，其中半球的半径为 0.5 m，涂覆厚度d= 2 cm，涂层介质相对介电常数εr= 36.0，相对磁导率μr= 1.0．由雷达散射截面(Radar Cross Section，RCS)的结果曲线可以看出，物理光学方法和多层快速多极子方法(Multi-Level Fast Multipole Algorithm，MLFMA)吻合良好，验证了程序的正确性．

图3 算法验证模型结果

图3(b)给出了频率为3 THz的平面波入射下导体立方体的单站雷达散射截面，结果与文献[8]中采用多层快速多极子方法结果一致．可以看出，物理光学方法用于计算太赫兹频段目标散射的有效性．

首先对图1(c)建立的粗糙表面的圆锥和锥柱模型分别进行网格剖分，根据菲涅尔反射系数，得出目标表面电流，进而采用物理光学进行仿真计算．图1(c)所示的表面粗糙圆锥目标，其底面半径为 16.25 mm，高H为 48.5 mm．图2(a)给出了表面粗糙锥柱目标模型，其底面半径为 16.25 mm，高H为 151.0 mm．表面随机起伏高斯粗糙面的均方根高度δ= 0.5 mm，相关长度lx=ly= 10 mm，涂覆介质的相对介电常数εr= (7.8，-1.6)，相对磁导率μr= (1.5，-0.7)，涂覆介质层厚度d= 0.05 mm．

在入射波频率分别为30 GHz、0.1 THz和0.3 THz的VV极化情况下，对比均方根高度δ= 0.2 mm 的粗糙表面圆锥与光滑圆锥的单站雷达散射截面如图4所示．从图中结果可以看出，对于模型尺寸相同的粗糙表面圆锥与光滑圆锥的单站雷达散射截面走势基本一致，随着入射角的增大，RCS增大，垂直于锥面照射时达到最大峰值．图4(a)为光滑圆锥与粗糙圆锥的结果基本上重合，RCS曲线较为平缓波动不明显，可以看出微波段目标表面的微粗糙度对RCS的影响很小，可以忽略; 图4(b)、图4(c)表明，太赫兹波段下光滑表面和粗糙表面的圆锥目标雷达散射截面出现较大差异，粗糙表面引起目标RCS曲线震荡起伏，并且频率越高，起伏越明显，曲线波动越大．故在太赫兹波段，粗糙度对目标的后向RCS影响相当明显，不可忽略．

图4 光滑表面与粗糙表面圆锥目标雷达散射截面

图5给出了入射波频率为0.3 THz、极化为VV的情况下，不同均方根高度的粗糙表面目标模型的后向RCS．从图5中可以看出，雷达散射截面与目标表面的几何轮廓是正相关的，最大值在垂直于锥面的照射方向如图5(a)所示．对于锥柱模型，不仅在垂直于锥面方向有峰值，在垂直于柱面方向时雷达散射截面达到最大值，如图5(b)所示．均方根高度δ= 0.2 mm 对应曲线与光滑的结果相比抖动较小，在均方根高度δ= 0.5 mm 时，曲线的起伏增大，均方根高度δ= 1.0 mm 的结果峰值已经被起伏抖动淹没．在太赫兹波段，对于同一频率不同粗糙度的目标，粗糙度越小，后向RCS曲线波动越平缓；粗糙度越大，RCS值曲线波动越大，高低起伏也越大，而且RCS曲线变化也越复杂．表明随着目标表面粗糙度的增大，反射变弱，散射范围扩大并且增强．

图5 不同均方根高度的粗糙表面目标单站雷达散射截面

对于均方根高度δ=0.5 mm的粗糙表面圆锥模型，图6给出了VV极化不同入射频率条件下目标的后向雷达散射截面．对于圆锥模型，频率f= 30 GHz 的微波段RCS曲线相对光滑，起伏较小，随着频率的增大，粗糙表面圆锥的后向RCS明显下降，且频率越高，RCS值下降得越多．RCS值曲线的波动也随着频率的升高而增大；对于锥柱模型，相对于圆锥模型较大且结构更复杂RCS曲线变化也越复杂．随着频率的升高，入射波的波长变小，目标表面的粗糙度与入射波长的比值增大，粗糙度引起的漫散射效应增大，表面粗糙度的作用严重影响了目标RCS曲线峰值变得不明显．

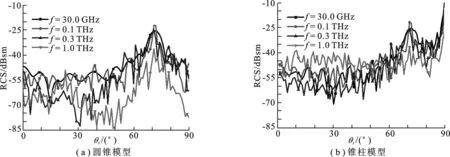
图6 不同频率粗糙表面目标雷达散射截面

图7给出了入射波频率为0.3 THz的不同涂层厚度的粗糙表面目标VV极化的后向RCS．可以看出，相对于导体情况表面，涂覆介质以后目标的雷达散射截面几乎在所有角度都有明显减小，并且随着涂层厚度d的增大，雷达散射截面持续减小．电磁波由自由空间经过涂覆介质层照射到目标内表面，当内表面为金属导体时，由于金属电导率很大，电磁波在金属表面全反射，反射电磁波经过介质涂层再次进入自由空间．涂覆介质层的厚度增大，电磁波在介质层中的传播距离增大，损耗增多．涂覆介质层对雷达散射截面的缩减有明显的作用；在一定范围内，随着涂层厚度的增大，涂覆介质对电磁波的吸收增加，粗糙表面目标的后向RCS减小．

图7 不同涂层厚度的粗糙表面目标雷达散射截面

图8给出了VV极化平面波入射波频率为0.3 THz粗糙度均方根δ= 0.2 mm 的圆锥模型涂覆不同介质材料雷达散射截面．低耗涂覆介质对RCS的缩减有一定的效果，随着相对介电常数εr实部增大，RCS变化不明显，如图8(a)所示．由图8(b)可以看出，VV极化条件下相对介电常数εr，虚部增大，RCS减小，效果明显．对于电性吸收材料，电导率是主要的损耗机理，而εr虚部刚好反映了电导率的作用．

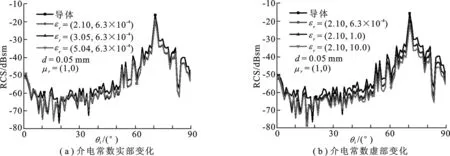
图8 涂覆不同介质材料粗糙圆锥目标雷达散射截面

4 结 束 语

文中采用了高斯粗糙面模拟随机环境的方法来建立高斯粗糙表面目标，通过均方根高度和相关长度来描述目标表面的粗糙度．根据菲涅尔反射系数得到表面电流分布，采用物理光学方法进行仿真计算，分别针对不同的入射波频率、不同粗糙度、不同涂覆材料以及不同涂层厚度的随机高斯粗糙表面目标模型在太赫兹波段的散射特性进行了分析．从分析结果可以得到以下结论：微波频段波长远大于目标表面微米级的粗糙度，粗糙度的影响可以不考虑；而在太赫兹波段，波长与粗糙度处于等量级，必须考虑到粗糙度对于散射结果的影响，并且入射波频率越高，波长越小，粗糙度与波长的比值越大，对散射的影响也越大．当目标表面有涂覆介质材料时，目标的雷达散射截面小于导体情况下的结果，在一定范围内涂层越厚，雷达散射截面的缩减越大．VV极化涂覆介质层的电导率即相对介电常数虚部，对于雷达散射截面的减小有明显作用．

参考文献：

[1] SUSHKO O, PIGEON M, DONNAN R S, et al. Comparative Study of Sub-THz FSS Filters Fabricated by Inkjet Printing, Microprecision Material Printing and Photolithography[J]. IEEE Transactions on Terahertz Science and Technology, 2017, 7(2): 184-190.

[2] 党文佳, 曾晓东, 来志, 等. 粗糙目标光外差信号特性对探测阈值的影响[J]. 西安电子科技大学学报, 2016, 43(4): 57-62.

DANG Wenjia, ZENG Xiaodong, LAI Zhi, et al. Effect of Properties from a Rough Target Echo Signal on the Detection Threshold in Optical Heterodyne Detection[J]. Journal of Xidian University, 2016, 43(4): 57-62.

[3] DANYLOV A A, GOYETTE T M, WALDMAN J, et al. Terahertz Inverse Synthetic Aperture Radar (ISAR) Imaging with a Quantum Cascade Laser Transmitter[J]. Optics Express, 2010, 18(15): 16264-16272.

[4] 王瑞君, 邓彬, 王宏强, 等. 太赫兹与远红外频段下铝质目标电磁特性与计算[J]. 物理学报, 2014, 63(13): 119-128.

WANG Ruijun, DENG Bin, WANG Hongqiang, et al. Electromagnetic Scattering Characteristic of Aluminoustargets in the Terahertz and Far Infrared region[J]. Acta Physica Sinica, 2014, 63(13): 119-128.

[5] 张存林, 牧凯军. 太赫兹波谱与成像[J]. 激光与光电子学进展, 2010, 47(2): 1-14.

ZHANG Cunlin, MU Kaijun. Terahertz Spectroscopy and Imaging[J]. Laser & Optoelectronics Progress, 2010, 47(2): 1-14.

[6] 杨洋, 景磊. 金属介电常数对雷达目标散射截面的影响[J]. 激光与红外, 2013, 43(2): 155-158.

YANG Yang, JING Lei. Impact of the Metal Permittivity on Radar Target Scattering Cross Section[J]. Laser & Infrared, 2013, 43(2): 155-158.

[7] 杨洋, 姚建铨, 张镜水, 等. 粗糙铜表面对低频太赫兹波的散射实验[J]. 红外与毫米波学报, 2013, 32(1): 36-39.

YANG Yang, YAO Jianquan, ZHANG Jingshui, et al. Terahertz Scattering on Rough Copper Surface[J]. Journal of Infrared and Millimeter Waves, 2013, 32(1): 36-39.

[8] LI Z, CUI T J, ZHONG X J, et al. Electromagnetic Scattering Characteristics of PEC Targets in the Terahertz Regime[J]. IEEE Antennas and Propagation Magazine, 2009, 51(1): 39-50.

[9] 程志华, 谢拥军, 马晓东, 等. 介质目标的太赫兹波近场散射特性计算[J]. 电子与信息学报, 2015, 37(4): 1002-1007.

CHENG Zhihua, XIE Yongjun, MA Xiaodong, et al. Near-field Electromagnetic Scattering Characteristics of Dielectric Targets in the Terahertz Regime[J]. Journal of Electronics & Information Technology, 2015, 37(4): 1002-1007.

[10] 李昌泽, 童创明, 王童, 等. 不稳定表面粗糙目标的太赫兹波段散射特性分析[J]. 强激光与粒子束, 2016, 28(4): 45-51.

LI Changze, TONG Chuangming, WANG Tong, et al. Analysis of Terahertz Wave Scattering Charactering of Unstable Rough Surface Target[J]. High Power Laser and Particle Beams, 2016, 28(4): 45-51.

[11] 陈辉, 吴振森, 白璐. 任意形状凸粗糙物体高斯光束相干散射研究[J]. 光学学报, 2005, 25(1): 115-120.

CHEN Hui, WU Zhensen, BAI Lu. Research on the Coherent Scattering of Gaussian Beam from ArbitrarilyShaped Convex Object with Rough Surface[J]. Acta Optica Sinica, 2005, 25(1): 115-120.

[12] WU Z S, CUI S M. Bistatic Scattering by Arbitrarily Shaped Objects with Rough Surface at Optical and Infrared Frequencies[J]. International Journal of Infrared and Millimeter Waves, 1992, 13(4): 537-549.

[13] 江月松, 聂梦瑶, 张崇辉, 等. 粗糙表面涂覆目标的太赫兹波散射特性研究[J]. 物理学报, 2015, 64(2): 90-96.

JIANG Yuesong, NIE Mengyao, ZHANG Chonghui, et al. Terahertz Scattering Property for the Coated Object of Rough Surface[J]. Acta Physica Sinica, 2015, 64(2): 90-96.

[14] 张连波, 郭立新, 苟雪银, 等. 三层粗糙面电磁散射的矩量法研究[J]. 西安电子科技大学学报, 2013, 40(6): 147-154.

ZHANG Lianbo, GUO Lixin, GOU Xueyin, et al. Method of Moment Investigation on Electromagnetic Scattering from the Three-layered Rough Interfaces[J]. Journal of Xidian University, 2013, 40(6): 147-154.

[15] 李杰, 郭立新, 何琼, 等. 复合电磁散射分析中的精确几何建模[J]. 西安电子科技大学学报, 2012, 39(6): 92-98.

LI Jie, GUO Lixin, HE Qiong, et al. Accurate Geometry Modeling in Analysis of Composite EM Scattering[J]. Journal of Xidian University, 2012, 39(6): 92-98.

[16] 朱艳菊, 江月松, 张崇辉, 等. 应用改进的物理光学法和图形计算电磁学近似算法快速计算导体目标电磁散射特性[J]. 物理学报, 2014, 63(16): 182-188.

ZHU Yanju, JIANG Yuesong, ZHANG Chonghui, et al. Fast Computation of Electromagnetic Scattering Characteristics from Conducting Targets Using Modified-physical Optics and Graphical Electromagnetic Computing[J]. Acta Physica Sinica, 2014, 63(16): 182-188.

[17] LI X, XIE Y, YANG R. High-frequency Method for Scattering from Coated Targets with Electrically Large Size in Half Space[J]. IET Microwaves, Antennas and Propagation, 2009, 3(2): 181-186.

ElectromagneticscatteringcharacteristicofGaussianroughcoatedobjectsinterahertz

ZHAOHua，GUOLixin

(School of Physics and Optoelectronic Engineering, Xidian Univ., Xi’an 710071, China)

The scattering characteristics of Gaussian roughness surface coated targets are studied in the terahertz (THz) band based on the Kirchhoff approximation and the physical optics (PO) method. Based on the Gaussian roughness surface, roughness surface cone and cone-cylinder models are built which are meshed according to the frequency of the incident wave to meet the PO calculation requirements. According to the Fresnel reflection coefficient, the current on the surface is calculated, and then the radar cross section (RCS) of the coating rough target is obtained. The RCS of the rough surface target are compared with the smooth target. Numerical results for the rough coated cone model and cone-cylinder model are given and discussed from different coating dielectric media, different coating thickness values, different angles of incidence, different frequencies, and different roughness values. The results show that the roughness of the target surface in the terahertz band has a significant effect on the scattering.

Gaussian rough surface; roughness surface target; terahertz; physical optics

2017-03-08

时间：2017-06-29

国家自然科学基金重点资助项目(61431010)；国家自然科学基金创新研究群体科学基金资助项目(61621005)

赵 华(1987-)，男，西安电子科技大学博士研究生，E-mail: zhaohuaxynu@163.com．

http://kns.cnki.net/kcms/detail/61.1076.TN.20170629.1734.010.html

10.3969/j.issn.1001-2400.2018.01.005

O441.4

A

1001-2400(2018)01-0023-07

(编辑： 齐淑娟)