圆钢管混凝土K型焊接相贯节点力学性能数值模拟
高春彦,杨卫平,李 斌
(1.内蒙古科技大学 土木工程学院,内蒙古 包头 014010; 2.南京航空航天大学 航空宇航学院,江苏 南京210016)
近年来钢管结构在工程中的应用日益广泛,相贯连接节点依靠其施工便利、视觉效果流畅、构造用钢量省,再加上没有附设的加劲零件,成为主流节点形式之一.随着节点承受的荷载越来越大,为了保障节点的强度,往往需要对节点进行加强,在钢管节点弦杆中填充混凝土是一种有效的加强手段,可以较大程度的提高节点的强度和刚度.目前,钢管混凝土相贯节点已广泛应用于格构柱、桁架、输电塔架、桥梁、海洋平台等结构中,国内外学者对其静力性能、疲劳性能以及抗震性能等进行了试验研究和有限元分析[1-6].但关于极限承载力的研究仍处于明显滞后的状态,导致设计依据不可靠,使得钢管混凝土相贯节点的设计要么过于保守,要么存在安全隐患.
本文在对圆钢管混凝土K型焊接相贯节点进行试验研究的基础上[7],建立了有限元参数分析模型,对试验试件进行了受力全过程分析,验证了有限元模型的有效性.本文中作者对该种节点进行了大量的参数分析,得到了各控制参数对节点极限承载力和承载效率的影响规律.基于文献[8-9]中空心圆钢管K型相贯节点冲剪破坏模式的极限承载力计算方法,计算了圆钢管混凝土K型相贯节点冲剪破坏时的极限承载力,并与有限元计算结果进行了比较.
1 有限元参数分析
1.1 计算参数
鉴于文献[7]中试验节点的数量有限,不能反映所有的节点破坏模式.为了全面研究圆钢管混凝土K型焊接相贯节点的破坏模式和极限承载力,对轴向荷载作用下节点的受力性能进行了有限元参数分析.节点模型如图1所示,其中d0、t0分别表示弦杆的直径和厚度;di、ti分别表示腹杆直径和厚度;g表示间隙;θ1、θ2分别表示受压腹杆、受拉腹杆与弦杆的夹角.
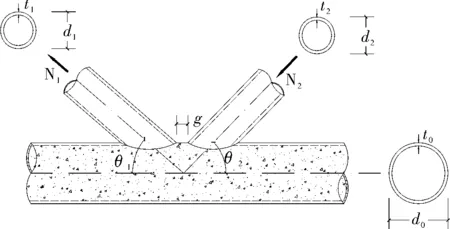
图1 节点模型Fig.1 Joint model
有限元参数分析时,弦杆直径均取为219 mm,两腹杆截面几何尺寸相同,腹杆与弦杆夹角θ1和θ2均为40°.计算时弦杆和腹杆长度取与试验试件相同,即弦杆长度为1 628 mm,腹杆长度为750 mm,可以消除边界条件对加载区域的影响.变化的几何参数主要包括弦杆径厚比γ、腹杆与弦杆管径比β和壁厚比τ.根据这3个几何参数,本文对γ取3个水平(36.5、55、73.5),β取3个水平(0.27、0.41、0.61),τ取6个水平(0.5、0.75、1、1.5、2、3),共设计了3×3×6=54个节点进行了非线性有限元分析,该种参数分析方法可全面细致地认识各个影响因素间的关系.
1.2 有限元计算模型
利用有限元程序ABAQUS建立有限元模型,首先对文献[7]开展的试验节点进行了计算分析,从破坏模式、荷载—变形关系、极限承载力、节点区塑性区域发展情况等方面,对有限元计算结果与试验结果进行对比,以验证有限元模型的有效性.
参数分析时钢管采用S4R壳单元,为了提高计算精度,其厚度方向采用9个积分点的Simpson积分,混凝土采用C3D8R三维实体单元.钢管材料采用二次塑流模型,钢材的屈服强度取为235 MPa;混凝土材料采用塑性损伤模型,塑性损伤模型中需要输入混凝土的受压与受拉性能参数.采用文献[10]提出的反映钢管约束效应的核心混凝土单轴受压应力—应变关系模型表达混凝土的受压行为,采用能量破坏准则考虑混凝土的受拉软化性能.混凝土的抗压强度标准值为26.8 MPa.
采用映射网格划分,由于圆钢管K型相贯节点各杆件交汇处的相贯线为几何构型复杂的空间曲线,实体单元和壳单元节点完全对齐的网格不容易获得,因此在腹杆接头处采用密度较大的网格单元,通过耦合的方式连接在弦杆钢管表面.
钢管与混凝土间的法向接触采用硬接触,切向采用库仑摩擦模型,摩擦系数取0.4.有限元模型的荷载—位移边界条件与试验试件的边界条件保持一致.即弦杆一端固定,另一端为定向支座,仅允许沿弦杆轴线方向有位移;两腹杆端部边界条件为滑动铰支座,仅允许沿腹杆轴线方向的位移,而约束其径向位移.计算简图如图2所示.采用位移加载的方式,采用Newton-Raphson方法进行迭代计算.模拟时没有考虑焊缝缺陷以及焊缝残余应力的影响.
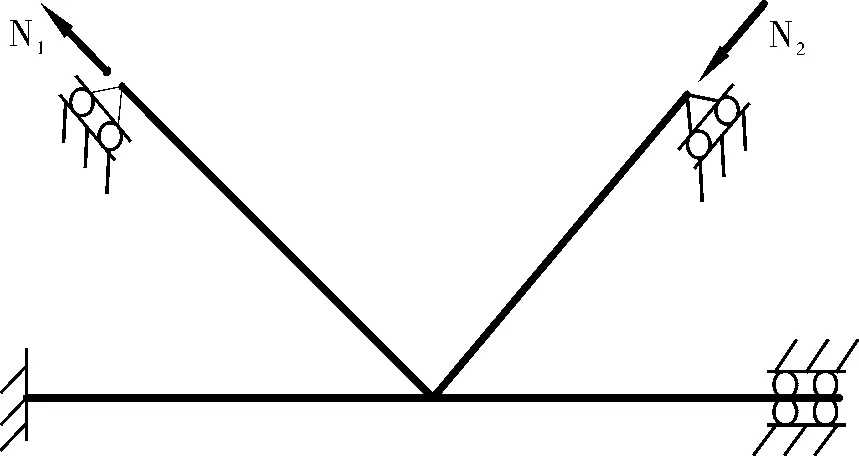
图2 计算简图Fig.2 Calculation diagram
2 节点破坏模式
与文献[7]中试验试件的破坏模式相比较,圆钢管混凝土K型焊接相贯节点达到极限承载力时共有3种破坏模式:受压腹杆局部屈曲或整体弯曲破坏、弦杆冲剪破坏以及联合破坏(如图3所示).在54个圆钢管混凝土K型焊接相贯节点中,总共50%(27个)的节点破坏属于受压腹杆失效,42.6%(23个)的节点破坏属于弦杆冲剪破坏,7.4%(4个)的节点破坏属于联合破坏.

图3 试件破坏模式Fig.3 Failure mode of the specimens
分析各试件的破坏模式可知,在τ值比较小或β值比较小的情况下,腹杆管壁较薄或管径较小,腹杆发生局部屈曲或整体弯曲破坏.该种情况下节点承载力取决于腹杆承载力.而不论弦杆管径比γ取何值,弦杆内混凝土的填充使得节点的强度和刚度大大提高,弦杆不会发生过度的塑性变形而失效.在γ值和τ值均较大时,弦杆壁厚较薄或腹杆轴向强度较大,会发生弦杆冲剪破坏,该种情况下节点承载力主要取决于弦杆的抗剪强度以及腹杆与弦杆连接面的表面积.在τ值相对较大时,受压腹杆失效会与受拉腹杆与弦杆接头处的冲剪破坏同时发生.
3 节点极限承载力计算方法
3.1 极限承载力判别准则
根据文献[11],空心圆钢管K型焊接相贯节点的极限承载力,取腹杆轴力极值和弦杆管壁极限变形这两个极限状态中先期到达者所对应的腹杆轴力.而圆钢管混凝土K型焊接相贯节点由于弦杆内混凝土的填充,不会发生弦杆塑性失效,主要破坏模式包括腹杆失效和弦杆冲剪开裂两种.因此,节点极限承载力可取腹杆失效时其端部的轴力极值与冲剪开裂破坏时作用在腹杆端部的轴力两者中的较小值.
3.2 腹杆失效时极限承载力
当腹杆失效时节点承载力可取腹杆截面的塑性承载力Py,即腹杆钢材的屈服强度与相应腹杆截面面积的乘积.为验证腹杆截面塑性承载力Py的有效性,图4中列出了Py与腹杆失效试件有限元计算承载力Pf的对比情况.从图4中可以看出,采用腹杆截面塑性承载力Py可以较好地计算腹杆失效时圆钢管混凝土K型焊接相贯节点的极限承载力,此时几何参数β、τ对节点极限承载力的影响较大,而γ值的影响很小.

图4 腹杆失效时Py与Pf的比较Fig.4 Comparison between Py and Pf when web fails
3.3 弦杆冲剪破坏时极限承载力
对于圆钢管混凝土K型焊接相贯节点,受拉腹杆与弦杆连接接头处的冲剪破坏问题变得较为突出,特别在弦杆壁厚较薄,腹杆较强的情况下,很容易发生弦杆管壁的冲剪开裂破坏.国际管结构发展与研究委员会(CIDECT)[8]中将弦杆的冲剪面面积与其抗剪强度相乘,得到空心圆钢管K型相贯节点基于冲剪破坏模式的承载力计算方法,如下式所示.
(1)
式中:fy为弦杆钢管抗拉强度;d为腹杆直径;t0为弦杆壁厚;θ为腹杆与弦杆的夹角.
本文作者考虑到弦杆内混凝土对受拉腹杆与其连接接头处冲剪开裂破坏的影响有限,因此可以采用CIDECT推荐的方法估算圆钢管混凝土K型焊接相贯节点的冲剪承载力.由公式(1)可以发现,当该类型节点发生冲剪破坏时,承载力除了与腹杆与弦杆间夹角θ有关外,主要与腹杆与弦杆管径比β、弦杆径厚比γ直接相关(本文算例中没有考虑θ的影响).
对于发生冲剪破坏和联合破坏(共有27个算例)的圆钢管混凝土K型相贯节点试件,将腹杆截面塑性承载力Py、CIDECT[8]计算得到的承载力P分别与有限元计算承载力Pf进行了比较(Py和P均为定值,所以在图中用水平线标示),比较结果如图5、图6所示.

图5 各参数下Py/Pf分布图Fig.5 Distribution map of Py/Pf
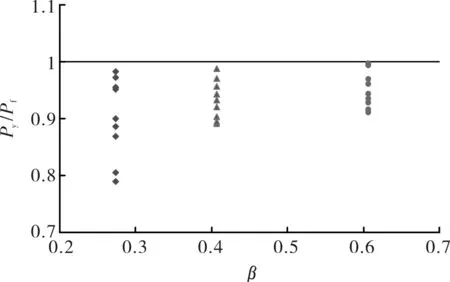
图6 各参数下P/Pf分布图Fig.6 Distribution map of P/Pf
从图5可以看出,当试件发生联合破坏时,Py/Pf比值接近于1;当试件发生冲剪破坏时,由于腹杆较强,Py/Pf的比值偏离1较多.说明当圆钢管混凝土K型相贯节点发生冲剪破坏时,如果利用腹杆截面塑性承载力Py来计算节点的承载力,计算值将远大于节点实际承载力,此时腹杆强度远远没有得到充分发挥,而在受拉腹杆与弦杆接头处已发生破坏.
从图6可以看出,各试件的P/Pf比值均小于1.说明不考虑弦杆内混凝土的有利作用,采用空心圆钢管K型相贯节点基于冲剪破坏时的承载力计算方法来分析圆钢管混凝土K型相贯节点并不太恰当.实际上,混凝土的存在一定程度上限制了弦杆受拉时的“椭圆化”[9],使得灌注混凝土后节点的冲切破坏承载力在一定程度上得到提高.因此,在接下来的研究中考虑圆钢管混凝土K型相贯节点与空心相贯节点两者间的衔接,建立一套适用于圆钢管混凝土K型相贯节点冲剪破坏时的极限承载力计算方法是非常必要的.
4 承载效率分析
为了考察圆钢管混凝土K型相贯节点的强度,这里引入承载效率的概念,即节点承载力和腹杆承载力的比值[12].为研究各种破坏模式下几何参数β、γ、τ对该类节点承载效率的影响,计算了54个试件的承载效率如图7所示,其中图7(a)为腹杆失效试件的承载效率,图7(b)为冲剪破坏和联合破坏试件的承载效率.从图7可以看出:
(1)腹杆失效试件的承载效率总体较高,在0.8~1之间.腹杆与弦杆管径比β对试件承载效率的影响是,随着β的增大,节点承载效率略有降低,但降低幅度不大.γ和τ对节点承载效率的影响也不大.
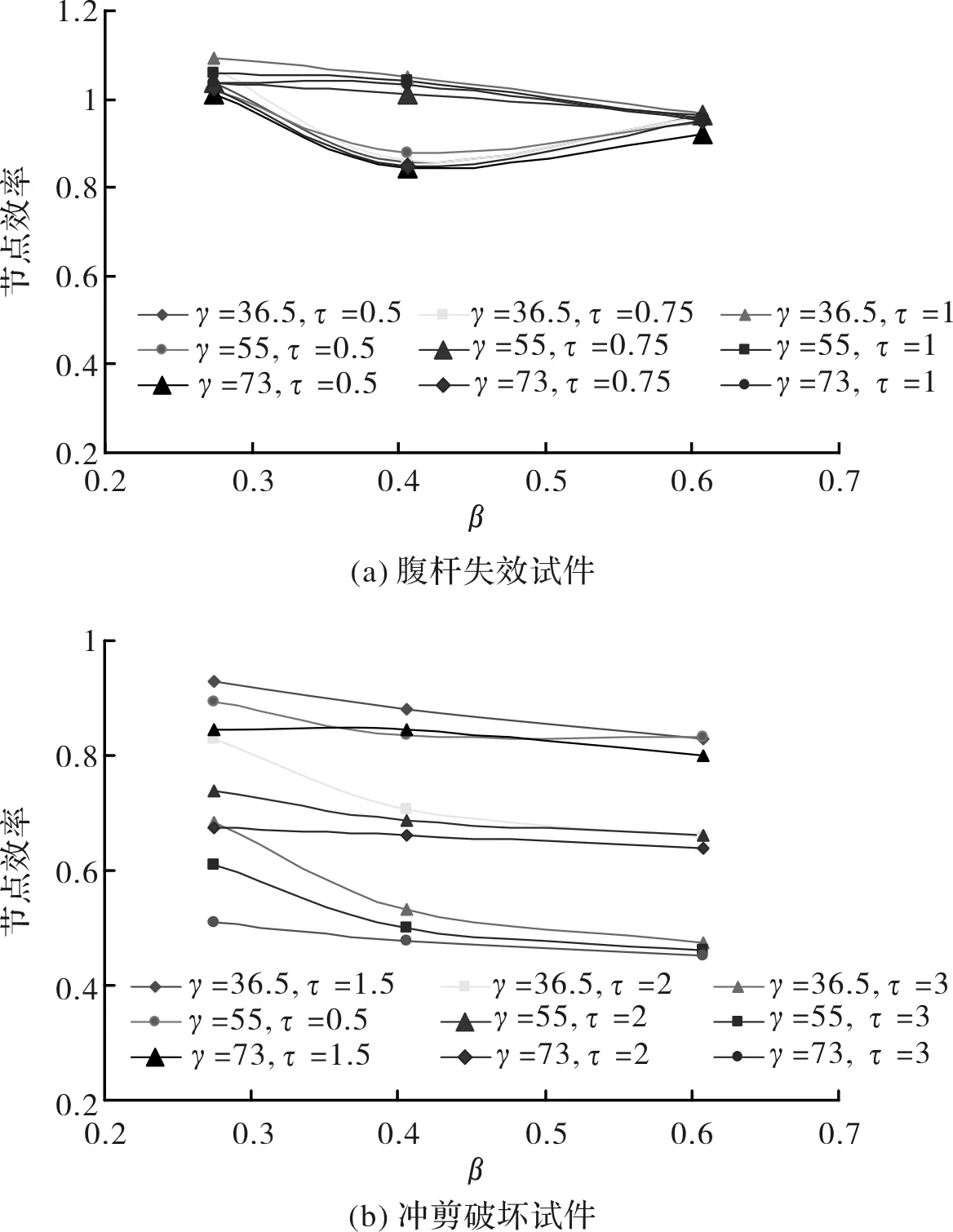
图7 β、γ、τ对试件承载效率的影响Fig.7 Effect of β、γ、τ on joint carrying efficiency
(2)冲剪破坏试件的承载效率相对较低.当γ、β相同时,随着τ的增加(即弦杆截面尺寸不变,腹杆直径不变而壁厚增加),节点的承载效率大幅度降低,此时受拉腹杆接头处弦杆的承载力变化不大,而腹杆强度增加较多,导致承载效率大大降低.当γ、τ相同时,随着β的增加(即弦杆截面尺寸不变,腹杆壁厚不变而直径增加),节点承载效率下降的幅度较缓,此时受拉腹杆接头处节点的承载力和腹杆强度均增加,但两者相比,腹杆强度增加的程度更大,导致节点承载效率小幅度降低.当β、τ相同时,随着γ的增加(即弦杆和腹杆的直径均不变而壁厚均减小),节点的承载效率降低,但降低幅度并不大,此时受拉腹杆接头处节点的承载力和腹杆强度均降低,且降低幅度相当,因此节点承载效率的降低幅度并不明显.
5 结论
(1)有限元分析表明圆钢管混凝土K型焊接相贯节点共有三种破坏模式:受压腹杆局部屈曲和整体弯曲破坏、弦杆冲剪开裂破坏以及联合破坏,控制节点破坏的关键参数是几何参数γ、β和τ.
(2)几何参数γ、β和τ对圆钢管混凝土K型焊接相贯节点承载力的影响与破坏模式相关联.当发生腹杆失效时,β和τ对承载力起控制作用,而γ的影响很小.当发生冲剪开裂破坏时,γ和β对极限承载力起控制作用,而τ的影响很小.
(3)几何参数γ、β和τ对圆钢管混凝土K型焊接相贯节点承载效率的影响也和破坏模式相关联.当节点发生腹杆失效时,承载效率总体较高,接近于1,各参数对承载效率的影响不大.当节点发生冲剪开裂破坏时,承载效率相对较低,其中τ的改变对承载效率的影响最大.
(4)采用空心圆钢管K型焊接相贯节点基于冲剪破坏模式的承载力公式计算了圆钢管混凝土K型焊接相贯节点的极限承载力,计算结果偏小,因此建立一套适用于圆钢管混凝土K型相贯节点冲剪破坏时的极限承载力计算方法是非常必要的.
参考文献References
[1] TEBBET I, BECKETT C, BILLINGTON C. The punching shear strength of tubular joints reinforced wit a grouted pile [C]//Proceedings of offshore Technology Conference, offshore technology conference association, Houston, Texas, 1979:915-921.
[2] SAKAI Y, HOSAKA T, ISOE A, et al. Experiments on concrete filled and reinforced tubular K-joints of truss girder[J]. Journal of Constructional Steel Research, 2004, 60:683-699.
[3] 陈宝春,黄文金.钢管混凝土K型相贯节点极限承载力试验研究[J].土木工程学报. 2009,42(12):91-98.
CHEN Baochun, HUANG Wenjin. Experimental study on ultimate bearing capacity of CFST directly-welded K-joints[J].China Civil Engineering Journal, 2009,42(12):91-98.
[4] 叶尹.大跨越钢管塔采用复合构件时的节点试验研究[J].电力建设.2007,28(12):39~42.
YE Yin. Experimental study on nodes of large span steel tube tower using composite components[J]. Electric Power Construction. 2007, 28(12):39-42.
[5] 宋谦益.圆钢管混凝土-钢管 K 形节点的力学性能研究[D].北京:清华大学,2010.
SONG Qianyi. Behavior of circular concrete filled steel tube to steel tube K-joints [D]. Beijing: Tsinghua University, 2010.
[6] 李斌,乔明,高春彦. 钢管混凝土格构式风电机塔架节点静力性能试验研究[J].建筑结构,2013,43(5):35-38.
LI Bin, QIAO Ming, GAO Chunyan. Static behavior study on latticed concrete-filled steel tubular wind turbine tower joints[J]. Building Structure, 2013,43(5):35-38.
[7] 高春彦,杨卫平,李斌,等. 风力发电机塔架K型相贯节点静力性能试验研究[J].西安建筑科技大学学报(自然科学版),2014,46(5):671-675.
GAO Chunyan, YANG Weiping, LI Bin, et al. Experiment study on the static behavior of the welded tubular K-joints in wind turbine tower[J]. J. Xi′an Univ. of Arch. & Tech.(Natural Science Edition),2014,46(5): 671-675.
[8] WARDENIER J, KUROBANE Y, PACKER J A, et al. Design guide for circular hollow section(CHS) joints under predominantly static loading [M]. 2nd ed. Altendorf, Switzerland:CIDECT, 2008.
[9] 王新毅. 圆钢管-圆钢管混凝土焊接节点抗弯刚度和极限承载力研究[D].上海:同济大学,2009.
WANG Xinyi. Research on the flexural stiffness and ultimate bearing capacity for the concrete-filled circle hollow section joint [D].Shanghai: Tongji University, 2009.
[10] 韩林海. 钢管混凝土结构理论与实践[M].北京:科学出版社,2007.
HAN Linhai. Theory and practice for concrete-filled steel tubular structure[M].Beijing: Science Press,2007.
[11] 李茂华,邢海军,胡晓光,等. 输电线路钢管塔小角度K形节点承载力研究[J].建筑结构.2013,43(5):48-53.
LI Maohua, XING Haijun, HU Xiaoguang, et al. Research on load-carrying capacity of smaller angle K-joints for power transmission steel tubular tower[J].Building Structure. 2013,43(5):48-53.
[12] 陈娟. 圆钢管混凝土T型相贯节点动力性能试验和理论研究[D].抗州:浙江大学,2011.
CHEN Juan. Experimental and theoretical study of dynamic performance of concrete-filled steel tubular T-joints[D]. Hangzhou: Zhejiang University, 2011.

