波形钢板混凝土界面间粘结滑移力学性能研究

王 威，李元刚，苏三庆，张龙旭，赵春雷，任 坦

(西安建筑科技大学 土木工程学院，陕西 西安 710055)

波形钢板混凝土(corrugated steel-plate concrete)结构指在混凝土中布置波形钢板，并配置一定的构造筋的组合结构.波形钢板截面几何形状由波谷、波脊、波峰组成，其中波谷与波脊或者波峰与波谷的内夹角称为波角，如图1所示.目前，国内外对于粘结滑移的研究主要以钢筋混凝土、型钢混凝土、钢管混凝土等为研究对象，并且从混凝土强度等级、横向箍筋配筋率、混凝土保护层厚度、混凝土浇筑方式等影响因素分析了其对粘结强度的影响[1-4]，对型钢混凝土粘结滑移本构方程[5-8]进行了研究.文献[3]从弹性力学角度建立了应力、滑移的理论公式，但缺乏试验数据验证理论公式精确性.然而，波形钢板混凝土粘结滑移的研究文献甚少.目前，波形钢板混凝土粘结滑移的研究大都以压型钢板混凝土组合楼板为研究对象[9-12]，主要从组合楼板高度、压型钢板厚度、剪跨比、剪力连接件的形式等因素对组合楼板的破坏形态、剪切粘结强度进行研究.波形钢板由于独特的截面几何性质，其波角、波脊、波峰几何参数的改变将对界面间粘结滑移产生很大影响.波形钢板与混凝土之间的界面粘结应力是两种材料安全工作的基础.研究清楚波形钢板混凝土粘结力学性能，掌握粘结滑移本构关系，对波形钢板混凝土结构受力分析有重要意义.工程设计人员充分考虑界面粘结力学性能，采用合理的计算理论，可以减少拉结筋、抗剪连接件的布置数量，进而减小工程造价.虽然有限元分析波形钢板混凝土构件受力性能需要的混凝土本构关系、钢材本构关系已相当成熟，但波形钢板与混凝土之间的粘结滑移本构关系少见文献报道.

图1 波形钢板几何截面Fig.1 Geometrical cross-section of corrugated steel plate

1 应力和位移公式推导

文献[12]通过压型钢板混凝土组合楼板剪切粘结滑移性能试验，得出压型钢板底面应力、应变沿剪跨长度呈指数分布规律，并提ε(x)=εmaxe-kx公式.k与混凝土强度、组合楼板高度有关.文献[5]对型钢混凝土粘结滑移进行了16个推出试件的试验，发现在荷载上升段，型钢翼缘和腹板的应变沿锚固深度(距加载端距离)呈指数分布；荷载下降段，型钢翼缘和腹板的应变沿锚固深度趋于线性分布.文献[6-8]也得出类似结论.据此类推：对于轴心拉拔(推出)荷载作用下波形钢板混凝土粘结滑移试验，波谷和波脊的应变分布规律也有类似情况.已知应变分布规律后，进而得出波形钢板轴向应力分布规律.根据力学平衡方程得知粘结应力是钢板轴向应力的微分，从而得知粘结应力分布规律.这为根据弹性力学应用半逆解法[13]求解任意锚固深度处的粘结应力和滑移提供了依据.事实上，波形钢板波脊面、波谷面、波角处粘结应力是不同的，并沿着锚固深度而发生变化.为方便力学分析，假定粘结应力τ(x)是指锚固深度x处的平均粘结应力.由于构件只受拉拔(推出)荷载，可以将波谷面外部混凝土分离出来，简化为平面应力问题，如图2所示.

1.1 荷载上升段时公式推导

1.1.1 混凝土应力公式

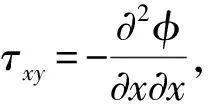
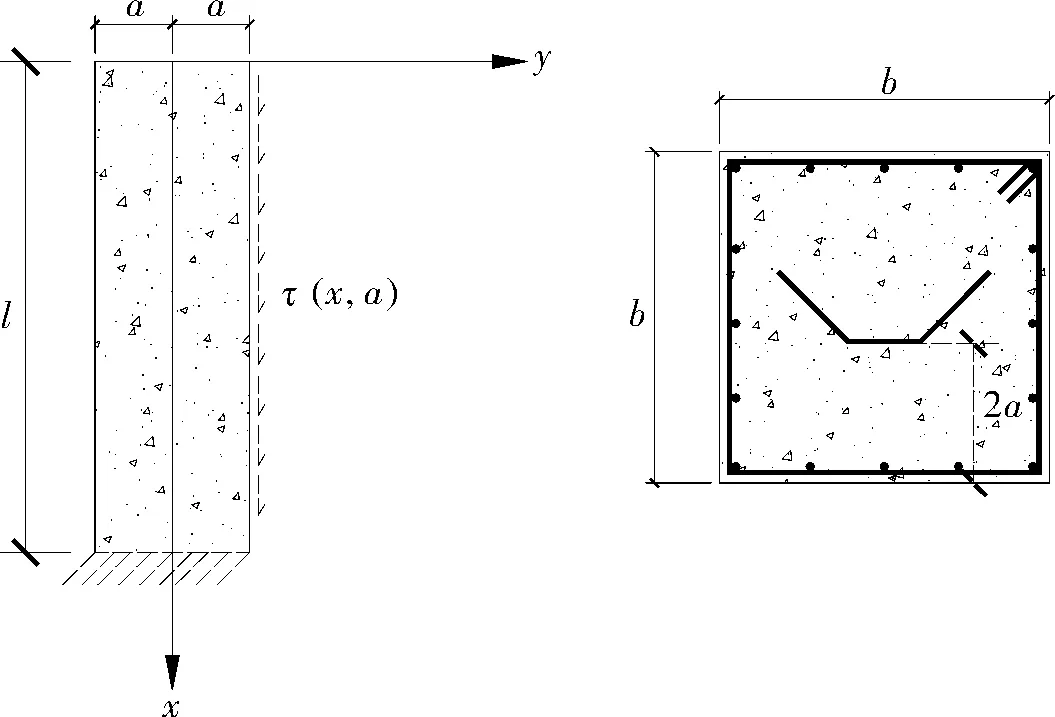
图2 计算简图Fig.2 Calculation chart

(1)

得出常系数微分方程：

k4f(y)+2k2f″(y)+f(4)(y)=0

(2)

解出：

f(y)=(c1+c2y)cosky+(c3+c4y)sinky

(3)

应力函数与应力分量有如下关系:

(4)

边界条件：

y=-a,σcy

|y=-a=0;y=-a,τxy

|y=-a=0

y=a,τxy

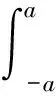
|x=1dy=0

将边界条件代入(4)，解得c1、c2、c3、c4如下:

(5)

(6)

(7)

(8)

1.1.2 混凝土位移公式

根据弹性力学几何方程得混凝土位移分量表达式为

(9)

将x=l,y=0,u

|x=ly=0边界条件代入uc表达式，得：

(10)

所以，混凝土位移公式如下：

(11)

1.1.3 波形钢板位移公式

取出波形钢板微段dx，受力如图3所示：

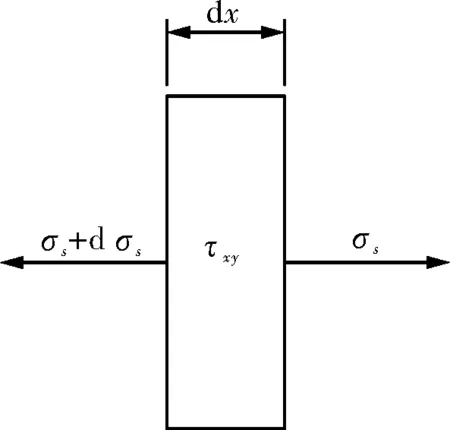
图3 应力分析Fig.3 Stress analysis

设h为板厚，根据力平衡方程有

(12)

(13)

滑移量就是混凝土与波形钢板在接触面上的位移差，联立式(11)、式(13)子，得

s=us-uc
|y=a

(14)

而粘结应力表达式为

τxy
|y=a=-kekxf1(a)

(15)

由式(11)、式(13)、式(14)知，在荷载上升阶段，滑移沿锚固深度呈指数与一次函数的复合分布形式.通过式(14)、式(15)可分别计算出在静荷载P作用下任意锚固深度处的滑移和粘结应力.

1.2 荷载下降段时公式推导

1.2.1 混凝土应力公式

在荷载下降段时，粘结应力沿锚固长度呈常数分布.设τ=τu(τu由试验确定，与荷载P有关)，假定应力函数φ(x,y)=(x+d)f(y).同上文小节所述，解出应力分量如下：

(16)

边界条件：

y=-a,σcy

|y=-a=0;y=-a,τxy

|y=-a=0

y=a,τxy

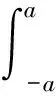
|x=0dy=0

将边界条件代入(16)式子，解得:

1.2.2 混凝土位移公式

同1.1.2节类似，求得位移表达式如下：

(17)

(18)

联立弹性力学中γxy分量的物理方程和几何方程由物理方程解得：

(19)

(20)

其中，任意常数u0、v0、ω为刚体位移，由约束条件定.同1.1.2节类似，只需满足y=0处即可.

解得常数u0、v0、ω后代入式(17)，得混凝土位移公式如下：

(21)

1.2.3 波形钢板位移公式

与1.13小节类似，得波形钢板位移公式如下：

(22)

这里，μs0物理意义是P=Pu时的加载端位移，由式(11)计算.

滑移表达式如下：

(23)

τxy
|y=a=τu

(24)

式(23)、式(24)为在荷载下降段时滑移量和粘结应力的理论公式.由式(23)可以看出，在荷载下降段时，滑移s沿锚固深度呈二次函数分布.

2 试验研究

2.1 试验方案

目前，推出试验法是型钢混凝土粘结滑移常用的试验方法.工程中波形钢板厚度一般在1.5～6 mm之间，且大多为开口型，其截面刚度小于型钢.因此，波形钢板混凝土推出试验法需考虑波形钢板加载端处的屈曲问题.文献[2-7]中，型钢与混凝土的接触面是全部粘结的.事实上，试件加载端处区域的应力是复杂的.根据弹性力学理论推导出的应力表达式无法精确满足次要边界条件(加载端、自由端)，只能采用圣维南原理进行静力等效.为验证波形钢板混凝土推出试验法的可行性，并考虑到混凝土浇筑方式、波形钢板混凝土界面粘结条件和波形钢板自身独特的截面几何因素，设计了5个试件，如表1所示.SC-1、SC-2、SC-3和SC-4试件混凝土强度等级为C30，试件尺寸为340 mm×240 mm×360 mm.SC-C为对比试件，试件尺寸为400 mm×400 mm×600 mm，混凝土强度等级为C20.SC-C试件在波形钢板两端1/3处涂抹黄油以消除加载端、自由端对局部区域粘结应力的影响.本文引用文献[5]中的内置式滑移传感器对SC-1、SC-2、SC-3、SC-4试件波形钢板埋置长度内部进行滑移测量.为全面研究波形钢板混凝土粘结应力分布机理，在试件波谷、波脊面上开槽并布置应变片，测点如图5所示.试件在结构实验室WAW-1000液压伺服万能试验机加载，如图4所示.

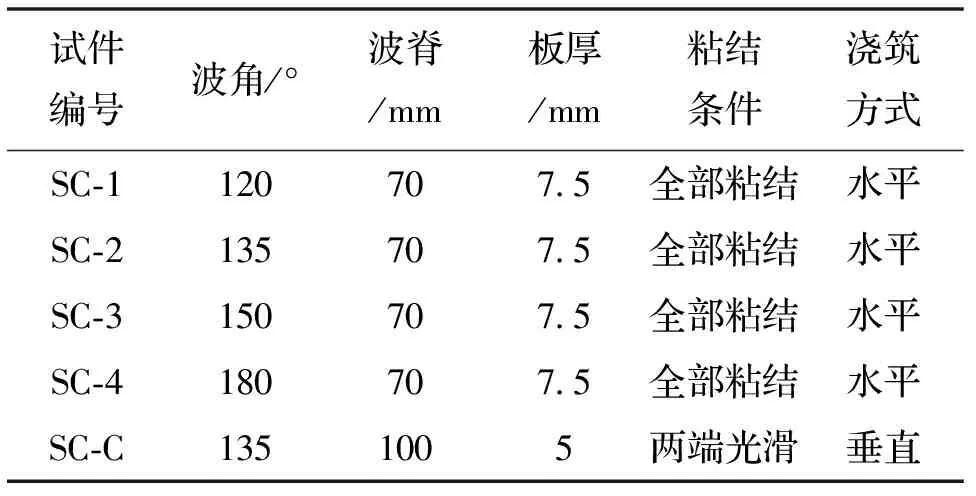
表1 波形钢板试件参数Tab.1 Parameters of corrugated steel-plate specimens

图4 试件加载装置(单位：mm)Fig.4 Test setup(unit:mm)

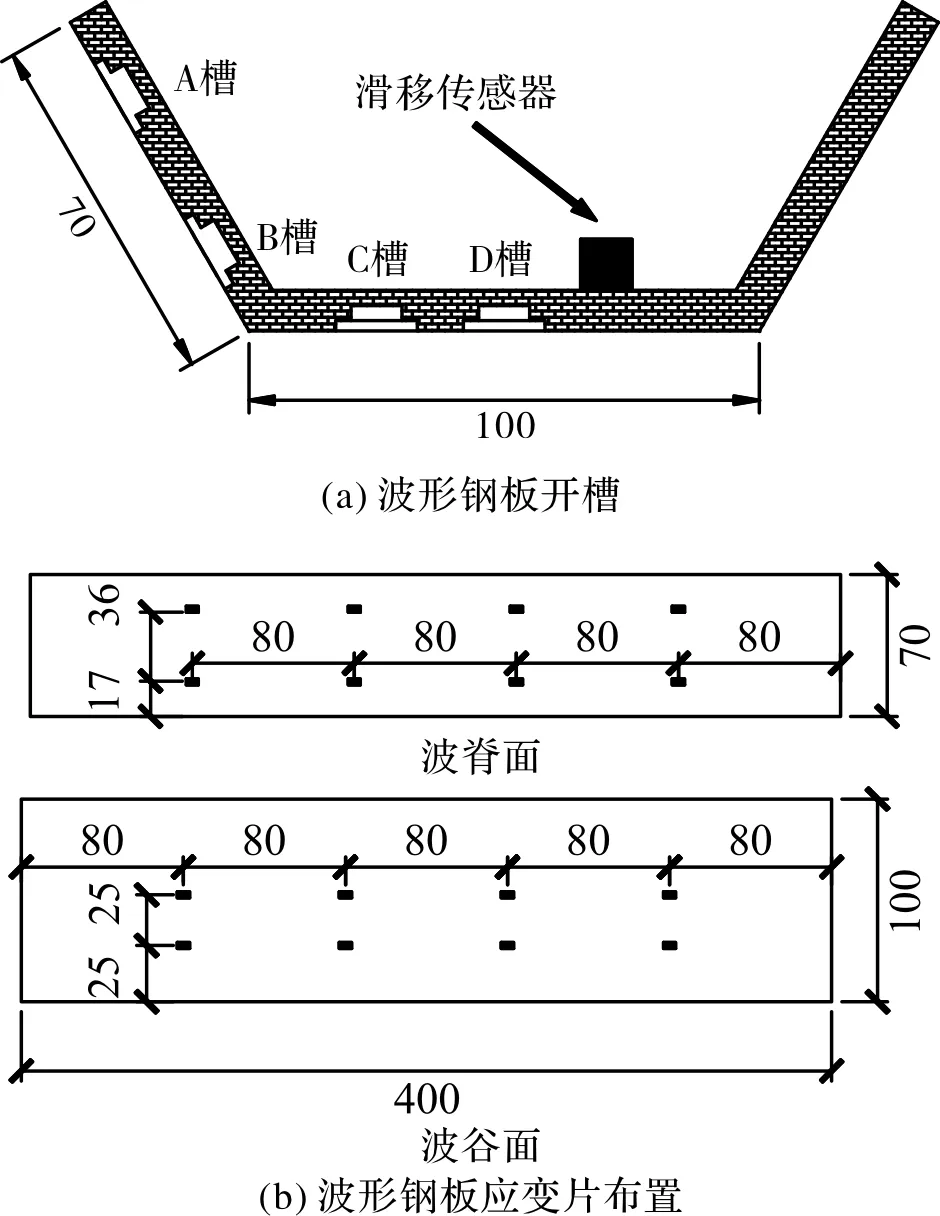
图5 测点布置图(单位：mm)Fig.5 Measuring points arrangement(unit:mm)

2.2 试验过程和现象

加载初期，SC-1、SC-2、SC-3、SC-4试件的滑移很小，荷载滑移曲线陡然上升.当荷载达到峰值荷载的30%～65%时，荷载滑移曲线出现拐点而变得平缓.在此过程中，试件没有裂缝产生.当滑移达到内置式滑移传感器量程极限5 mm时，滑移传感器相当于抗剪栓钉，SC-1、SC-2、SC-3、SC-4试件的荷载滑移曲线再次出现拐点，斜率变大，荷载快速上升.该拐点对应荷载称为摩擦荷载Pm，对应的滑移记为Sm.试件开始出现裂缝.试件裂缝首先从自由端处波脊尖端径直沿着最短路径穿过试件底部边缘，然后自下而上垂直蔓延.随着滑移继续增大，滑移传感器被剪切破坏后，试件承载力下降.SC-C试件加载初期没有滑移，当加载至极限荷载的5%左右时，试件开始产生明显滑移.SC-C试件在整个试验过程中没有出现混凝土裂缝等明显试验现象，这是因为波形钢板两端1/3长度区域涂抹了黄油，与混凝土接触面光滑.再者，箍筋至波形钢板距离较远，减弱了箍筋对波形钢板的约束作用.发现试件两端抹黄油区域十分光滑，中间粘结区有混凝土碎片.各试件破坏形态如图5所示，荷载滑移曲线如图6所示.

图5 试验破坏图Fig.5 Specimen failure

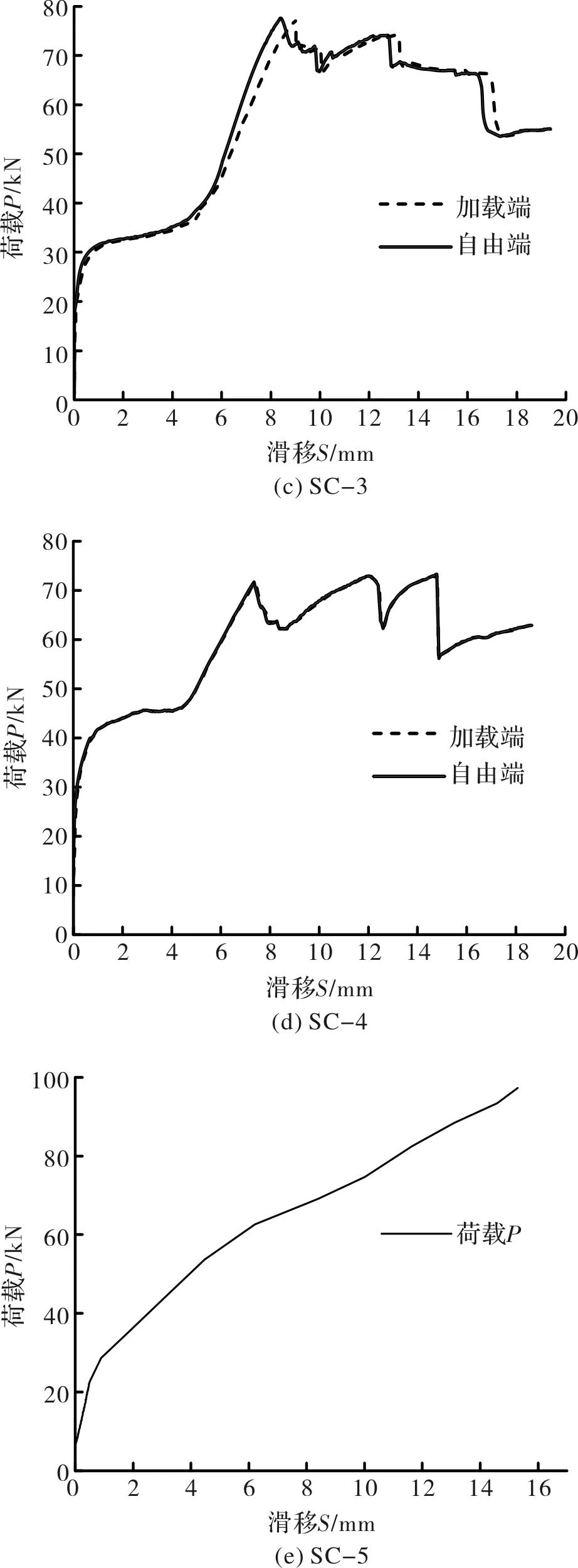
图6 荷载滑移曲线Fig.6 Load-slip curve

2.3 荷载滑移曲线研究

分析图6各试件的荷载滑移曲线，取前6个拐点，统一表示成图7所示.

图7 荷载滑移曲线分析Fig.7 Analysis of load-slip curve

(1)微滑移阶段(OA段)：粘结力主要由化学胶着力组成，荷载滑移曲线陡然上升.当滑移达到0.5 mm时，曲线出现拐点，该拐点对应的荷载定义为微滑移荷载Ps，对应的滑移记为Ss.

(2)滑移阶段(AB段)：粘结力主要由波形钢板与混凝土之间的摩擦力组成.当滑移达到内置式滑移传感器量程5 mm时，曲线再次出现拐点，该拐点对应荷载称为摩擦荷载Pm对应的滑移记为Sm.

(3)破坏阶段(BC段)：内置式滑移传感器开始发挥出抗剪栓钉作用，荷载滑移曲线陡然上升.此阶段粘结力主要由机械咬合力和摩擦阻力组成.试件自由端和加载端有细小裂缝产生并逐渐发展.荷载滑移曲线以较大斜率上升，直到内置式滑移传感器附近处的混凝土被压碎后，达到极限荷载Pu.

(4)荷载滑移曲线下降阶段(CD段)：当滑移传感器出现不同形态的破坏，此时荷载达到极限，曲线出现下降段.试件自由端、加载端裂缝发展充分，试件侧面产生裂缝.

(5)荷载滑移曲线后发展阶段(DE段)：此阶段曲线上升或下降取决于滑移传感器的破坏形态.当波形钢板孔洞被滑移传感器固定杆挤压变形严重后，造成滑移传感器脱落，荷载滑移曲线出现台阶状下降，如SC-1、SC-3试件.SC-2、SC-4试件的荷载滑移曲线出现上升是由于滑移传感器尚未脱落只是金属盒被挤压破坏，曲线出现短暂的下降段(CD段)，接着曲线继续上升(DE段).当滑移传感器脱落，荷载滑移曲线才出现台阶状下降.试件的最终残余阶段是试件所有滑移传感器脱落后，荷载维持一个定值.

2.4 粘结强度分析

(25)

(26)

式中，波角θ在120°～180°范围内.当θ为180°即平钢板时，粘结强度最大.另外，由图6(e)计算SC-C试件的粘结强度值为0.69 MPa，大于其他4个试件，表明垂直浇筑的混凝土试件粘结强度大于水平浇筑的试件.

图8 波角对粘结强度的影响Fig.8 Effect of wave angle on bonding strength

2.5 波形钢板表面应变分析

图9为各试件在微滑移荷载Ps的应变沿锚固长度的分布规律.从图可以看出，应变沿锚固长度大致呈指数分布.波角和波脊处的应变要大于波谷轴心的应变值.

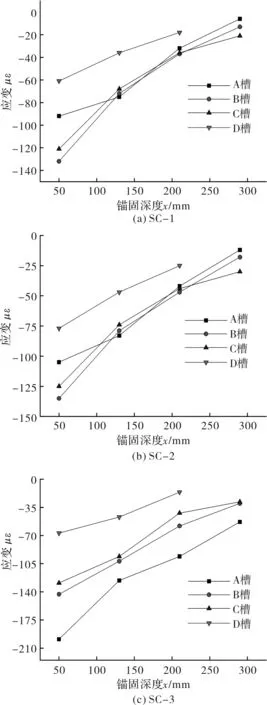
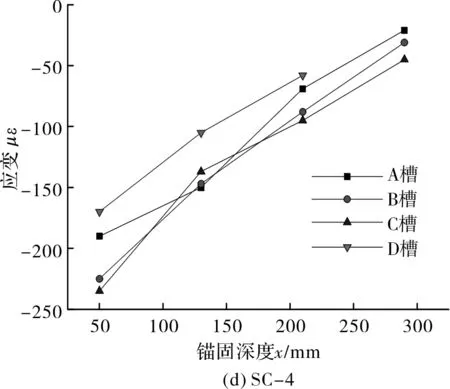
图9 Ps时试件应变分布Fig.9 Strain distribution of specimen at Ps load

图10为波形钢板全截面力学分析，根据力学平衡方程可推得：

(27)

图10 波形钢板全截面力学分析Fig.10 Mechanical analysis of the full cross section of corrugated steel plate

(28)

图11 等效应变分布Fig.11 Equivalent strain distribution

从图11看出，波形钢板等效应变可用下式分布函数表示：

ε(x)=η1εmax-η2εmaxe-k1x

(29)

式中：η1、η2为调整系数，εmax为试件加载端局部最大应变值；k1为波形钢板等效应变特征值,其通过式(30)计算

k1=(7.59-0.029θ)/1 000

(30)

2.6 波形钢板表面等效粘结应力分析

经统计回归，等效应变特征值与波角关系如图12所示，发现等效应变特征值k1与波角呈线性函数关系.联立式(27)、式(28)，得波形钢板等效粘结应力如式(31)所示.本试验中对试件进行了开槽，削弱了局部板厚，导致槽口处局部应力大于其他地方.因此，需折算成同等板厚的等效粘结应力.其分布规律，如图13所示.

(31)

图12 等效应变特征值与波角关系Fig.12 The relationship between equivalent strain eigenvalue and wave angle

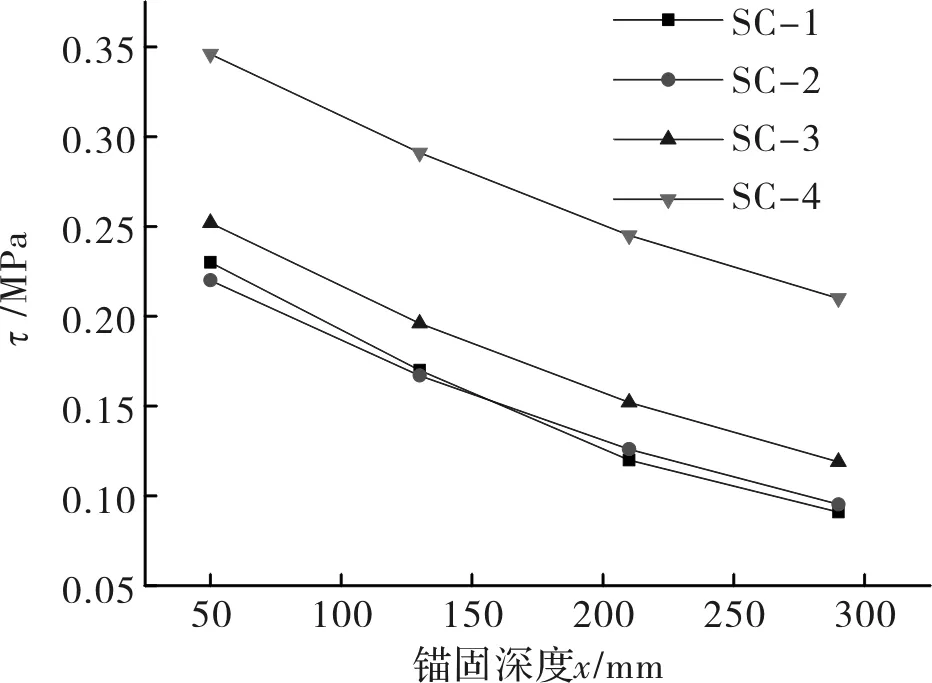
图13 等效粘结应力分布Fig.13 Equivalent bond stress distribution

3 理论公式与试验结果的验证

3.1 粘结应力的验证

根据第二节等效应变特征值k1计算公式，代入各试件的波角θ得到k1值，令k1=-k代入第一节相关理论公式，解出系数c1、c2、c2和c4，进而粘结应力τ(x)理论值，并与试验值作比较.

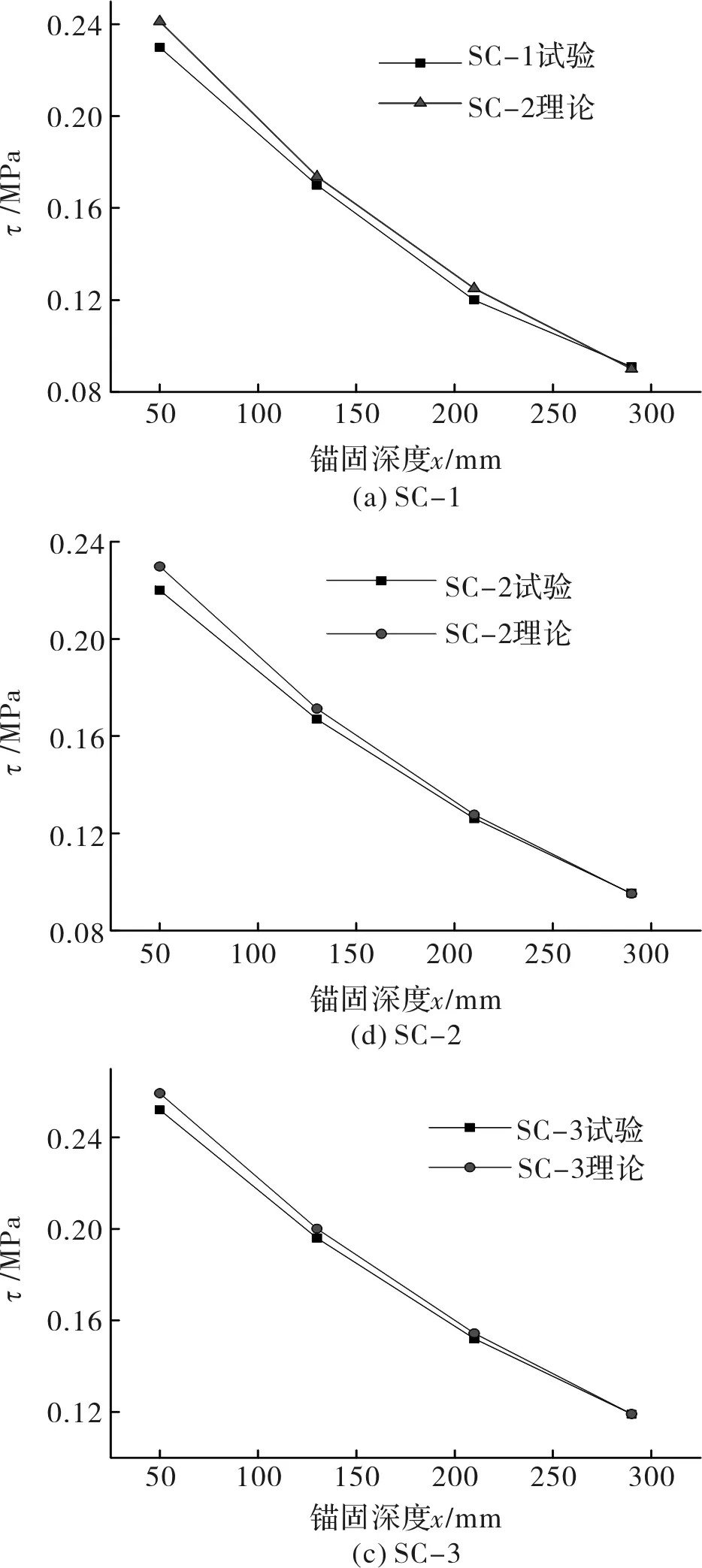
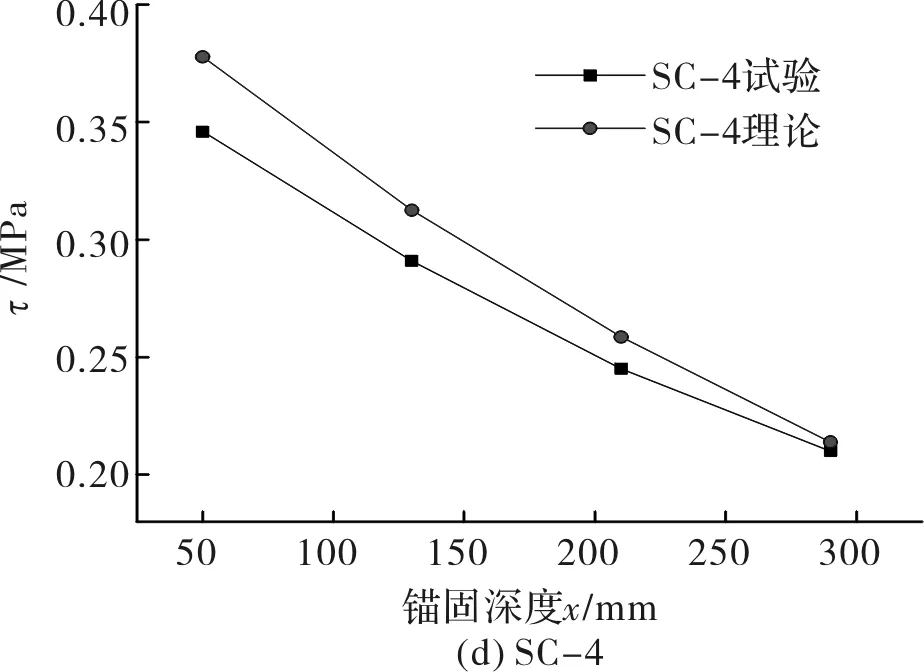
图14 粘结应力理论解与试验解的对比Fig.14 Bond stress of the contrast between the theoretical solution and test solution

从图14发现，根据弹性力学理论公式计算的粘结应力和试验获得的等效粘结应力吻合较好.

4 结论

(1)根据弹性力学理论推导了波形钢板与混凝土拉拔(推出)试验中各自的应力、位移、滑移的理论公式.

(2)研究了基于推出试验的波形钢板混凝土粘结滑移的试验方法.根据试验结果，建立了粘结强度与波角的计算公式.对于波角为钝角的波形钢板混凝土，粘结应力随着波角的增大而增大.

(3)通过SC-C对比试件，表明混凝土垂直浇筑方式的试件粘结强度高于水平浇筑的试件.

(4)波形钢板混凝土在推出荷载作用下，波角、波脊处的应变大于波谷轴心处的应变；同时，应变沿锚固深度呈指数分布函数.提出了波形钢板等效应变特征值的计算公式.

(5)根据试验结果，得出了波形钢板混凝土界面粘结力理论公式中的特征值系数k1，并与试验得出的等效粘结应力作对比，发现两者吻合很好，表明波形钢板混凝土基于弹性力学的粘结应力理论计算公式具有精确性.

参考文献References

[1] 肖季秋, 钟树生, 邹良明. 劲性钢筋混凝土粘结性能的试验研究[J]. 四川建筑科学研究, 1992(4):2-6.

XIAO Jiqiu, ZHONG Shusheng, ZOU Liangming. Experimetal study on bond performance of stiffened reinforced concrete[J].Sichuan Architecture Science Study, 1992(4):2-6.

[2] 刘灿, 何益斌. 劲性混凝土粘结性能的试验研究[J]. 湖南大学学报(自然科学版), 2002(S1):168-173.

LIU Can, HE Yinbin. Experimental study on bond behavior of steel reinforced concrete[J]. Journal of Hunan University (natural sciences edition) , 2002(S1):168-173.

[3] 郑山锁, 杨勇, 薛建阳,等. 型钢混凝土粘结滑移性能研究[J]. 土木工程学报, 2002, 35(4):47-51.

ZHENG Shansuo, YANG Yong, XUE Jianyang, et al. Research on bond-slip properties of steel reinforced concrete[J]. China Civil Engineering Journal, 2002, 35(4): 47-51.

[4] 孙国良, 王英杰. 劲性砼柱端部轴力传递性能的试验研究与计算[J]. 建筑结构学报, 1989, 10(6):40-49.

SUN Guoliang, WANG Yingjie. Experimental study and calculation of the axial force transmission performance of stiffened concrete column[J]. Journal of Building Structures, 1989, 10(6):40-49.

[5] 杨勇，郭子雄,薛建阳，等.型钢混凝土粘结滑移性能试验研究[J].建筑结构学报,2005,26(4):1-9.

YANG Yong, GUO Zixiong, XUE Jianyang, et al. Experiment study on bond slip behavior between section steel and concrete in SRC structures[J].Journal of Building Strctures,2005,26(4):1-9.

[6] 郑山锁, 邓国专. 型钢混凝土结构粘结滑移本构关系研究[J].哈尔滨工业大学学报, 2005,37(S1):524-527.

ZHENG Shansuo, DENG Guozhuan. Study on bond-slip constitutive relationship of steel reinforced concrete composite structures[J].Journal of Harbin Institute of Technology, 2005,37(S1):524-527.

[7] 郑山锁, 邓国专, 杨勇,等. 型钢混凝土结构粘结滑移性能试验研究[J]. 工程力学, 2003, 20(5):63-69.

ZHENG Shansuo, DENG Guozhuan, YANG Yong, et al.Experimental study of bond-slip performance between steel and concrete in SRC structures[J]. Engineering Mechanics, 2003, 20(5):63-69.

[8] 薛建阳, 赵鸿铁, 杨勇,等. 型钢混凝土柱粘结滑移性能及ANSYS数值模拟方法研究[J]. 建筑钢结构进展, 2006, 8(5):8-16.

XUE Jianyang, ZHAO Hongtie, YANG Yong, et al. Research on the bond-slip behavior and numerical simulation of steel reinforced concrete columns by ANSYS program[J]. Progress in Steel Building Structures, 2006, 8(5):8-16.

[9] 詹建敏, 吴炎海. 压型钢板-混凝土组合楼板剪切粘结承载力试验研究[J]. 福建建筑, 2002(3):27-30.

ZHAN Jianmin, WU Yanhai. A test research on the horizontal shear-bond capacity of composite slabs[J]. Fujian Architecture & Construction, 2002(3):27-30.

[10] 史庆轩, 郝家欢, 张兴虎. 压型钢板-混凝土组合楼板剪切粘结滑移性能的试验研究[J]. 哈尔滨工业大学学学报, 2007,39(S1): 329-332.

SHI Qingxuan, HAO Jiahuan, ZHANG Xinghu. Experiments on shear-bond-slip behavior of steel deck and concrete composite slabs[J]. Journal of Harbin Institute of Technology,2007,39(S1):329-332.

[11] 白力更, 赵辉, 史庆轩. 压型钢板-混凝土组合楼板剪切-粘结试验研究[J]. 钢结构, 2005, 20(3):30-34.

BAI Ligeng, ZHAO hui，SHI Qingxuan. Shear-bond experimental study of cold-formed steel deck and concrete composite floors[J]. Steel Construction, 2005, 20(3):30-34.

[12] 郝家欢.压型钢板-混凝土组合楼板剪切粘结滑移性能试验研究[D].西安：西安建筑科技大学，2007.

HAO Jiahuan. Experimental study on shear bond-slip behavior of profiled sheeting concrete composite slabs[D].Xi′an Univ. of Arch. & Tech., 2007.

[13] 徐芝伦. 弹性力学(上册)[M].4版.北京:高等教育出版社,2006.

XU Zhilun. Elasticity Mechanics(Vol.1)[M].4th ed. Beijing: Higher Education Press,2006.