基于反求设计的车身曲面重构研究

孔琳 陈芳

（西安航空职业技术学院航空制造工程学院 陕西 西安 710089）

引言

1 T-样条曲面重构原理

T-样条曲面的方程为[5]：

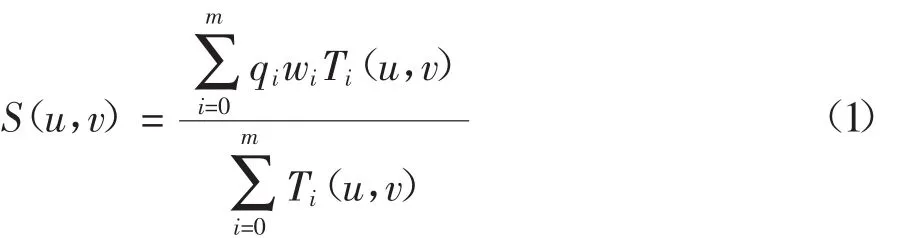
式中：S为曲面方程；qi为曲面中相应的控制顶点；wi为权重因子；Ti（u，v）为T-样条的基函数。基函数的定义为：

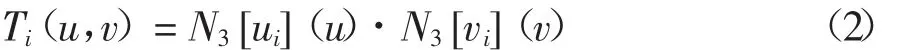
式中：N3[ui]（u）、N3[vi]（v）为 3 次 B-样条基函数的节点区间，ui=[ui0，ui1，ui2，ui3，ui4]、vi=[vi0，vi1，vi2，vi3，vi4]。

2 车身曲面重构

车身曲面的重构大致可分为3个步骤：三角网格参数化、T网格构造和曲面重构[6]。

2.1 车身三角网格曲面优化

车身曲面是车辆设计中最为复杂的部分，也是车辆制造的重点。为了更好地构建车身曲面，基于散乱点云的重构技术被广泛应用。为提高该技术的应用效率，在对车身重构前，人们往往会对车身的三角网格曲面进行参数处理，为三角网格几何和拓扑信息的处理奠定基础。但是，将一个三维网格曲面从三维空间映射到二维平面中，会造成其面积、长度、角度等出现扭曲[7]。三维网格参数化技术是在映射过程中，尽量使其中的几何度量不出现变化,进而对保角和保面积提出了更高的要求。对此，本文提出了三角网格参数化法对T-样条曲线进行求解。

2.1.1 三角网格参数化原理

在三角网格曲面ST=[V，E，T]的任一三角面片建立局部坐标系，顶点的局部坐标为Zi=（xi，y）i，i=1，2，3。已知该三角网格存在N个定点、n个三角面片。S（ui，v）i为参数曲面对应的方程，Pi=S（ui，v）i，则S的逆映射为：U（∶x，y，z）→（u，v，0），由此，在每个三角面片上均满足柯西—黎曼等式：

如图5(c)所示,设网络中包含50个节点,那么网络的拓扑状态信息包含在50×50像素的灰度图像内,状态图中每个像素点代表节点对间的链路,像素颜色深浅对应该链路的连接总时长,黑色表示0,白色表示切片时长T,灰色是时长在0～T之间的一个值.

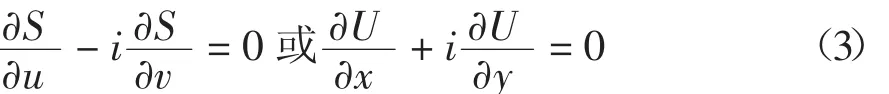
定义目标映射U的保角能量函数为ξT，表示三角网格角度扭曲的最小值。由此，ξT可表示为：

式中：t为三角网格曲面中的一个三角面片，可表示为：

式中：j为第j个顶点；1，2，3表示三角形中的3个顶点；M为投影在z=0上且由Z1，Z2，Z3构成的三角形面积的2倍。

令 u1=x1，v1=y1；u2=x2，v2=y2，则需要对 N-2个顶点的参数进行求解。同时，令Q=（QN-2Q2），Q=（qi，j）为n×N阶矩阵，QN-2对应的是前面N-2个未知参数，Q2对应的是后面2个参数。如第j个顶点在第i个三角形上，则有：

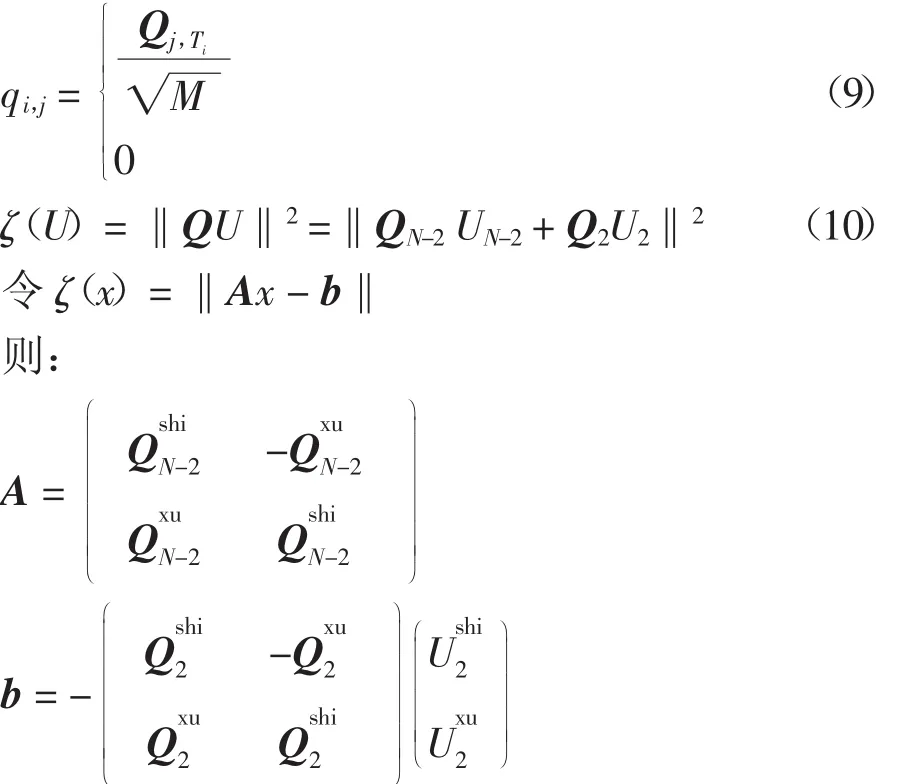
式中：shi代表复数的实部；xu代表复数的虚部。要得到最小值U，则令：

本文借助共轭梯度算法对H x=w的参数进行求解[8]。该方法是根据已知点处的梯度，构造一组共轭方向，进而沿着该方向进行搜索，从而求出目标函数的极值。算法流程图如图1所示。

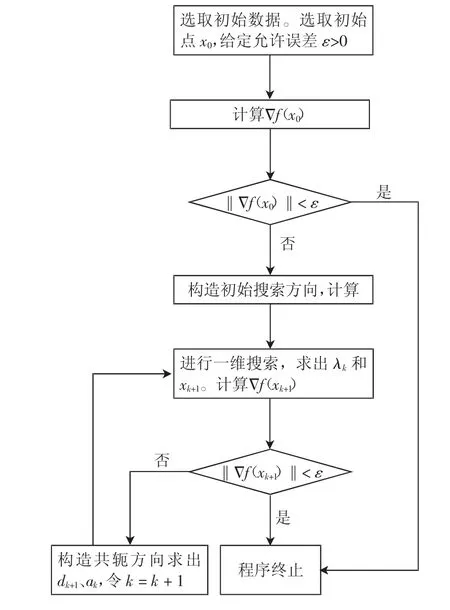
图1 共轭梯度算法流程

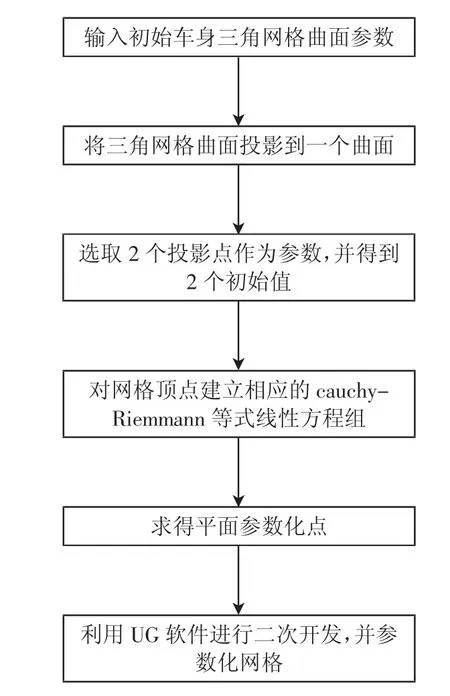
图2 网格参数化具体流程

2.1.2 三角网格参数化的实现

三角网格参数化是曲面重构的重要部分，通过三维到二维的参数转换，更利于对参数进行计算，更容易反求出控制顶点，以便实现对曲面的重构。本文通过最小二乘法保角映射算法，结合共轭梯度法完成对三角网格曲面的参数化。具体步骤如图2所示。

2.2 T网格构造

T网格构造是T-样条车身曲面重构的关键，主要是因为它的每个控制顶点所对应的基函数都是在T网格上得到的。从理论角度来看，T网格的生成无约束条件，只要满足定义，都可生成任意的T网格。通常情况下，为降低重构的资源消耗以及提高曲面重构的质量，会在采样点密集的地方增加控制顶点，反之则减少控制顶点。本文引入四叉树算法对T网格进行构造。在对T网格进行构造中，关键是定义最大细分次数n以及网格所包含的最大数据点m。通过这2个条件来判断细分是否可以结束。具体步骤如下：

1）确定细分的边界。在点云数据中找到u、v的最小值和最大值，通过这4个值，得到一个矩形细分区域；

2）对矩形区域内点的个数进行计算，如果得到的个数大于m，就在该矩形区域内插入一个点，将该点与4条边的中点连接，构成一个新的四边形。如此反复，直到让每个矩形区块内的数据点的个数都小于m。

2.3 T-样条下的曲面重构

在三角网格ST=[V，E，T]及其对应的T网格中，Q=（q1，q2，Kqm）表示网格中待求顶点的集合，V=（p1，∧pn）表示原始数据点。该T网格所对应的T-样条曲面可通过对应的曲面S来拟合给定的三角网格面，得到网格面到曲面S的最小距离。具体的目标方程为：

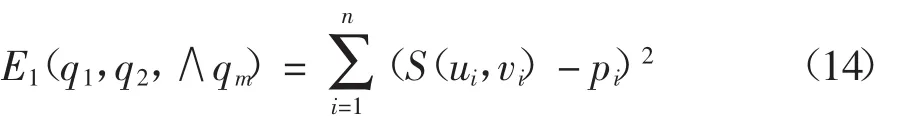
式中：（ui，vi）为点云数据在T-样条上对应的参数值。如果想得到对应的光顺曲面，通常会在重构曲面中添加一个光顺能量函数E2，从而得到新的目标能量方程：

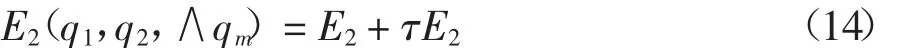
式中：τ的取值在0.01~0.1之间。当达到最小值时，得到控制顶点集合Q。

根据上述步骤，得到整体的曲面重构流程，如图3所示。

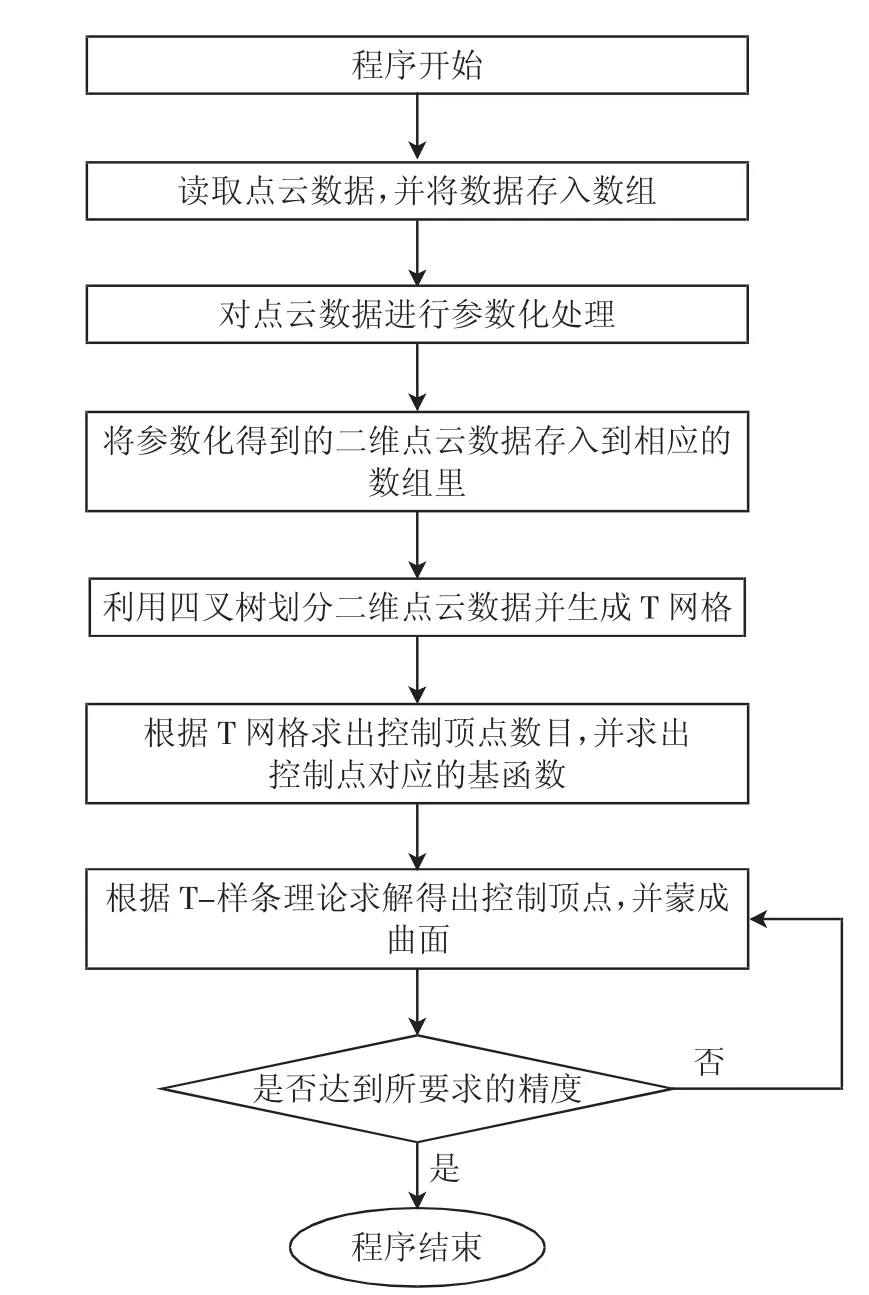
图3 T-样条曲面重构算法流程图

3 试验验证

3.1 车身重构UG开发

为完成对车身曲面的重构，结合UG软件进行二次开发。在UG软件中增加“车身点云预处理”按钮，用于对T-样条曲面的重构。通过该命令按钮，可得到如图4所示的模块。

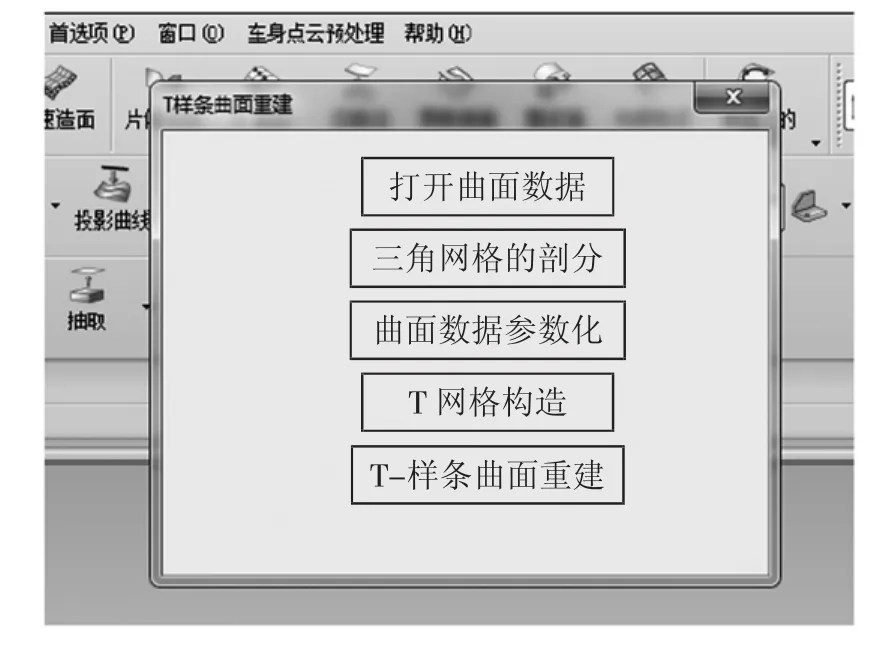
图4 命令按钮

3.2 改进结果

为验证上述方案的可行性，以汽车轮包曲面的开发为例，通过上述软件得到如图5所示的重构曲面。

图5 汽车轮包重构界面

为进一步验证上述方法与其他方法的优劣，本文将NURBS曲面重构方法与本文设计的算法所得到的车灯效果进行对比，得到如图6所示的结果。

图6 基于NURBS曲面和基于T-样条的车灯曲面重构图对比

从图5可以看出，通过重构后的车身曲面光滑。从图6可以看出，由本文所设计的T-样条得到的车灯重构曲面优于由传统的NURBS曲面所重构的车灯曲面，验证了本文所提出的设计方法的有效性。

4 结论

1）随着现代汽车制造业的不断发展，采用反求方法对车身进行设计，对缩短开发周期具有极其重要的意义。

2）车身点云曲面重构作为反求设计的核心，关键是如何借助T-样条提高车身曲面重构质量。

3）本文通过引入三维网格参数化的方式，提高了维度转换的精度；通过T网格的构造，为车身重构奠定了基础；通过构建车身曲面最小目标方程，并引入光顺能量函数，得到了新的车身曲面；通过UG软件编程开发，验证了本文所提出的设计方法的可行性，拓展了UG的逆向重构功能。

1 刘炀，陈曦，石鸽娅，等.逆向工程技术在曲面重构及检测中的应用[J].组合机床与自动化加工技术，2012（1）：51-53，57

2 王苏洲，舒志兵，姬振营.轿车车身覆盖件中逆向工程的应用[J].工具技术，2017，51（2）：107-110

3 彭小新，唐月红.自适应T样条曲面重建[J].中国图象图形学报，2010，15（12）：1818-1825

4 唐月红，李秀娟，程泽铭，等.隐式T样条实现封闭曲面重建[J].计算机辅助设计与图形学学报，2011，23（2）：270-275

5 王晓辉，刘清荣，郭楠.基于逆向工程的三维曲面重构软件的研究[J].赤峰学院学报（自然科学版），2015，31（3）：44-45

6 彭广威.基于逆向工程的汽车前围板曲面重构[J].机械工程师，2015（4）：110-112

7 何龙.逆向工程的车身三维造型数字化技术[J].华侨大学学报（自然科学版），2015，36（3）：252-257

8 李丹.基于逆向工程的汽车覆盖件曲面重构技术研究[J].机械设计，2016（8）：113-116