涡轮增压器轴承体温度场分析与研究

金文华 倪计民 白炳仁 李佳琪

（同济大学汽车学院 上海 201804）

引言

自1905年瑞士工程师艾尔弗雷德·比希发明涡轮增压器至今，涡轮增压器的发展已经走过了100多年的历史[1-2]。随着增压器转速与增压比的不断提高（最高转速已超过200 000 r/min，增压比可达3~3.5），涡轮增压器轴承体等零部件的工作环境越来越恶劣。涡轮增压器在运行时承受来自废气的高温热流，高温容易使润滑油温度过高，降低了润滑油的粘度和承载能力，造成轴与轴承座之间的磨损[3-4]。过高的温度会使密封环因积碳严重而丧失弹性，即出现高温松弛现象，一方面使废气向轴承体泄露，使轴承体内部润滑油的温度进一步升高，使轴承润滑条件恶化；另一方面使润滑油进入涡壳，发生漏油现象。为了保证增压器正常工作，一般希望涡轮端轴承部位温度不超过150℃，密封环部位温度不超过230℃[5]。

增压器轴承体的冷却性能直接影响着涡轮增压器的可靠性，并在很大程度上决定了涡轮增压器的使用寿命。本文以某款柴油机涡轮增压器为研究对象，对轴承体温度场分布及传热特性进行了数值模拟分析和试验验证，对可能引发超温风险的结构和运行因素进行了研究和分析。

1 数值模拟基础

1.1 计算流体动力学控制方程

轴承体传热仿真计算涉及对流体传热及流动方程的求解，主要包括涡轮端废气流体域、轴承体处润滑油流体域、隔热罩内部空气夹层及周边大气环境等。采用Navier-Strokes方程对所涉及到的流体域方程进行求解，包括质量守恒方程、动量守恒方程和能量守恒方程等，这些方程构成了计算流体动力学的控制方程[6]。

质量守恒方程为：

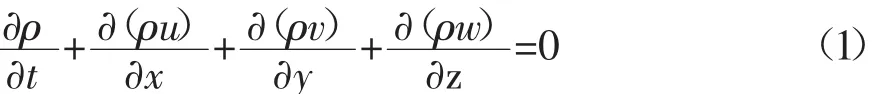
式中：t为时间，s；ρ为流体密度，kg/m3；u、v、w 分别为速度矢量¯u在 x、y、z坐标的分量。

根据牛顿第二定律，动量守恒方程可由偏微分方程描述为：

式中：μ 为动力粘度，N·s/m2；SMx、SMy和 SMz为动量守恒方程的广义源项；p为压力，Pa。

根据热力学第一定律，能量守恒方程可由偏微分方程描述为：

式中：cp为比热容，J/（mol·K）；T为温度，K；h为流体传热系数，W/（m2·K）；ST为粘性耗散项，J，即流体的内热源以及流体的粘性作用使其机械能转换为热量的部分。

用标准k-ε湍流模型封闭上述控制方程可得到：

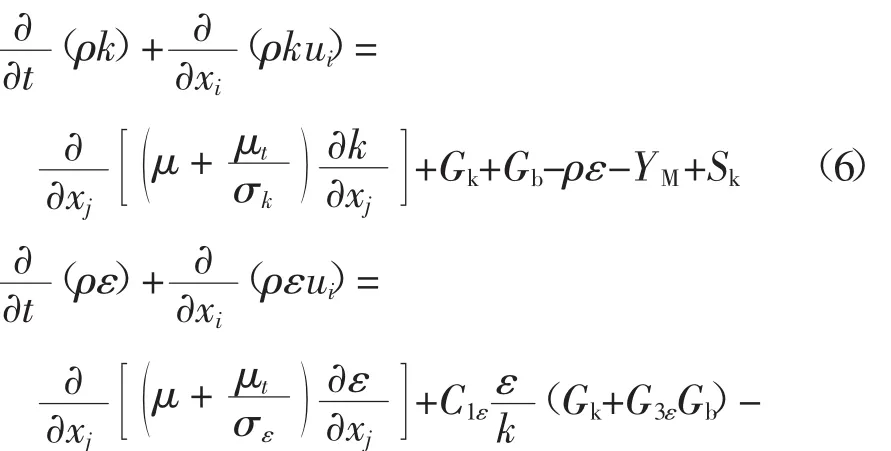
式中：Gk表示由平均速度梯度引起的湍动能的产生项；Gb表示由浮力引起的湍动能的产生项；YM为在可压缩湍流中脉动扩张对整体耗散率的贡献；C1ε、C2ε和 C3ε为经验常数，通常 C1ε=1.44，C2ε=1.92，C3ε在主流方向与重力方向平行时为1，在主流方向与重力方向垂直时为0；σk及σε为k方程和ε方程的湍流Prandtl数，通常 σk=1.0，σε=1.3；Sk和 Sε为用户自定义源项，通常 Sk=0，Sε=0[7]。

1.2 轴承体传热机理

轴承体的热源来源于涡轮端废气，热量传递包括热传导、热辐射以及流体-固体交界面的共轭传热等。本文不考虑热辐射的影响，从热传导和共轭传热等2方面阐述轴承体传热机理。

热传导发生部位主要在轴承体本体和转子轴。描述其温度分布的导热微分方程为：

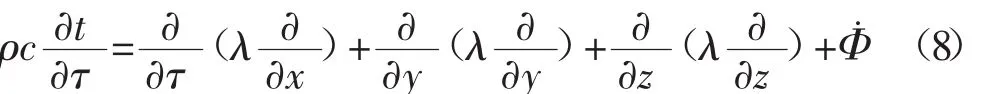
式中：Φ觶为内热源生成热，J。

轴承体中发生在流体-固体交界面上的共轭耦合传热主要存在于2个区域，一个是隔热罩内部的空气夹层与隔热罩及轴承体的交界面；另一个是润滑介质与润滑油油道的交界面。本文选用直接耦合法对交界面上的共轭耦合传热进行求解，使流体-固体交界面本来难以确定的外边界条件变为内边界条件，在交界面处只存在热流连续和温度连续的约束条件：

2 轴承体传热分析

2.1 研究对象

本文所研究的涡轮增压器，其匹配机型为6缸柴油发动机，排量为6.0 L，额定功率为92~132 kW。这种柴油机多用于工程机械、卡车、客车、柴油发电机组等工业机型。该涡轮增压器采用润滑油冷却，轴承形式为全浮动轴承，其三维模型如图1所示。

2.2 涡轮流体域三维模型

涡轮流体域存在旋转域，因此将整个流体域分为3部分，即进气流道、叶轮流道和出口流道等。涡轮端几何模型及流体域模型分别如图2和图3所示。

图1 涡轮增压器整机三维模型

图2 涡轮端几何模型

图3 涡轮流体域

2.2.1 计算边界条件

选用ANSYSCFX作为求解器，涡轮流体域中的工质均设为理想气体。热量传输模型采用全热模型（totalenergy），此模型在热焓的基础上，考虑了流体带来的热量变化，适用于高速流体及可压缩流体的热量传输计算。涡轮增压器的最高转速为110 000 r/min，因此选定50 000~110 000 r/min之间工况点进行仿真计算，各具体工况下的边界条件见表1。

2.2.2 仿真结果分析及气动性能验证

将计算结果导入CFD-POST进行后处理分析，得到各个转速工况下叶轮表面及叶轮背盘的温度分布。转速为110 000 r/min工况下叶轮表面及背盘的温度分布云图如图4所示。

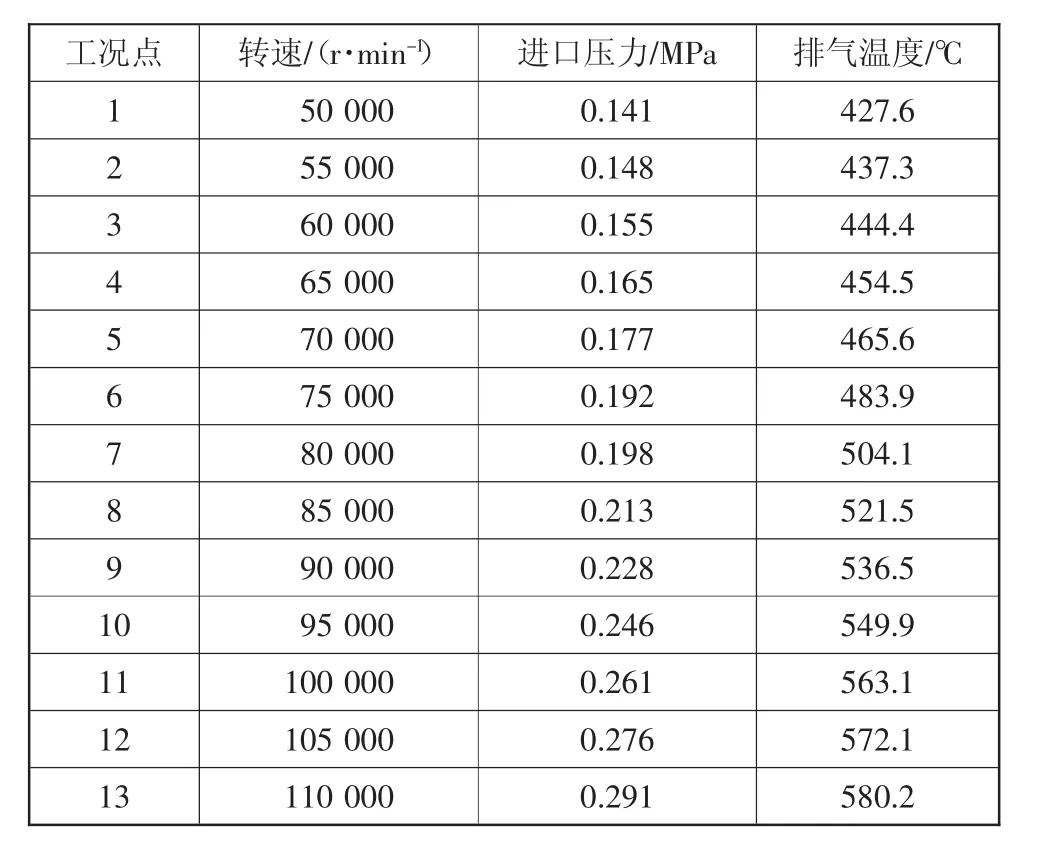
表1 仿真计算边界条件

图4 叶轮表面及背盘温度分布

气流以涡壳为导向装置，在涡壳内膨胀加速，压力和温度降低。在涡壳出口处速度达到最大，继之气流进入工作叶轮，在叶轮内继续膨胀，推动叶轮做功。沿着涡轮进口至涡轮出口，温度逐步降低。在涡壳出口处温度最高，涡轮出口处温度下降幅度可达173~203℃。涡轮转速越高，因废气做功增加，温度下降值越大。在涡轮叶轮表面，压力面由于与废气直接接触，温度明显高于吸力面，而背盘的温度比叶轮温度更高。

为了验证涡轮流体域仿真计算的准确性，对该款涡轮增压器在增压器整机试验台上进行基于表1工况点的热吹试验。选取涡轮流量、出口温度及等熵效率等3个指标作为验证参数，各工况对比结果如图5所示。

从图5可以看出，3个指标仿真结果与试验数据较为吻合，涡轮流体域仿真模型满足后续计算要求。其中折合流量最大偏差为6.8%，出口温度最大偏差为8℃，等熵效率最大偏差为4.4%。等熵效率在低转速工况下数据有误差，原因是仿真计算时将涡壳壁面边界条件设置为绝热，而在实际情况下，高温涡轮会向低温中间体及周围大气传递热量，使涡轮端出口温度在膨胀做功的基础上进一步降低，所测得的等熵效率会相应偏高。当转速升高后，热量传递对于等熵效率的影响不再明显。

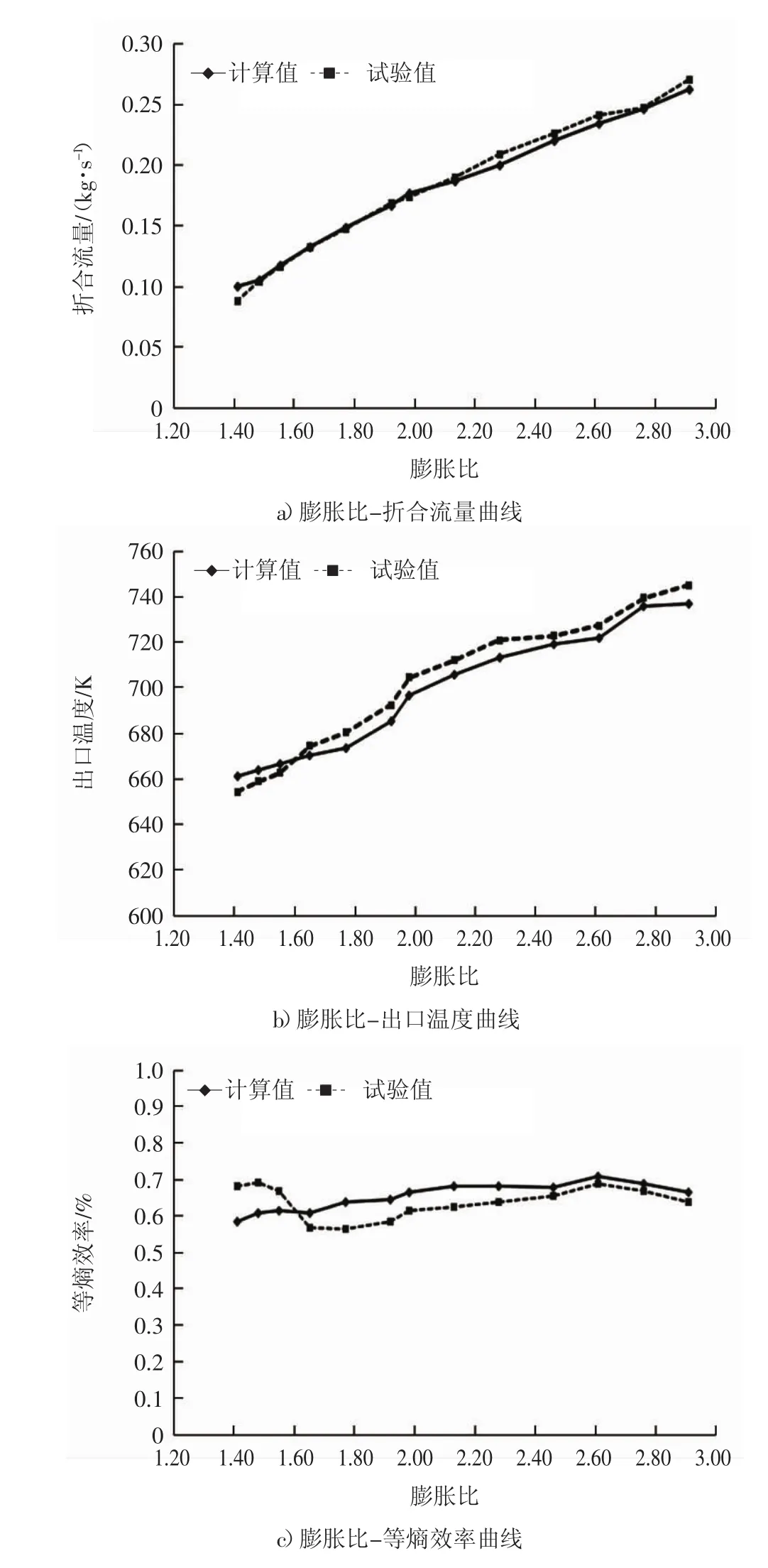
图5 仿真与试验结果对比

2.3 轴承体三维传热模型

2.3.1 模型简化

涡轮增压器轴承体是增压器转子部件的支承体，除了承受转子部件的机械负荷外，还承受涡轮端传来的热负荷。轴承体结构复杂，包含的零部件众多，因此在仿真计算时对其进行结构简化，忽略其中部分零件。图6为简化后的轴承体三维模型剖切图，去除了浮环轴承、止推轴承、止推套、密封环、卡箍等小部件，保留中间壳体、转子轴、隔热罩等3个主体部件。

图6 轴承体三维几何模型

2.3.2 边界条件及材料属性设置

将上述涡轮流体域模型计算所得的叶轮表面温度及叶轮背盘温度通过传输文件以数据传递的方式输入到轴承体三维传热模型，作为叶轮的温度边界条件。

温度场的求解，除了对边界条件进行设定外，还需对材料属性进行定义。本文所用涡轮增压器各部件材料见表2。

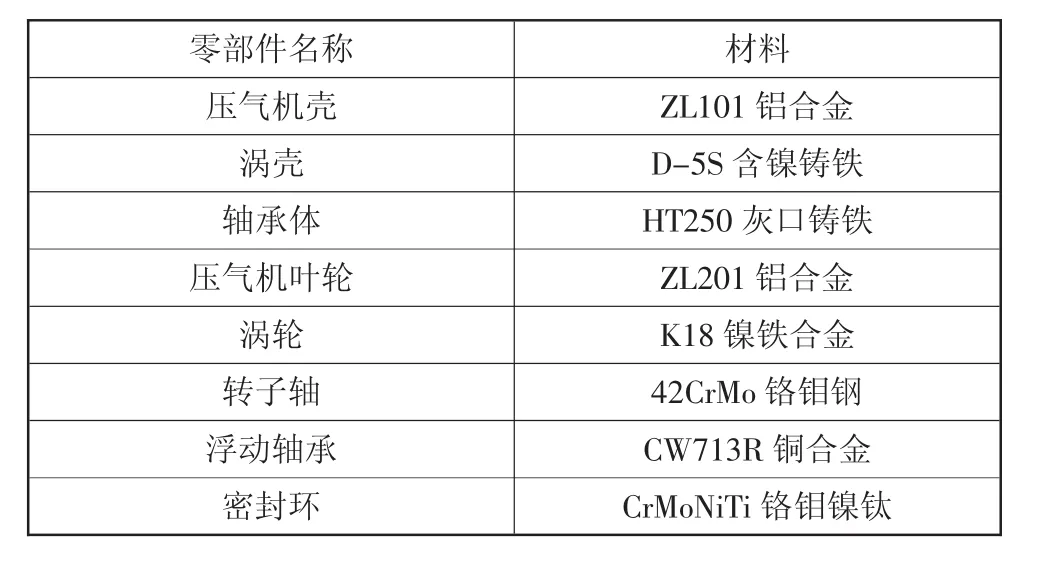
表2 涡轮增压器零部件所用材料

由于轴承体温差较大，如果将材料的导热系数设为定值，会造成一定的计算误差，不能得到准确的温度场梯度。因此，通过查询常用材料属性表，获得相关材料导热系数随温度的变化值，然后通过曲线拟合，得到导热系数与温度的关系方程，其中：

空气的方程为：

润滑油导热系数随温度变化不大，根据试验所用润滑油型号，将其导热系数设定为0.124 4W/（m·K）。

2.3.3 仿真结果分析

图7与图8分别为增压器最高转速为110 000 r/min工况下轴承体yz平面切面及轴承体外壁面的温度分布云图。从图7与图8可以看出，涡轮端温度明显高于压气机端。原因是隔热罩起到了良好的隔热作用。隔热罩空气夹层两端的温度差为367℃，说明隔热罩与轴承体间的空气夹层有效地阻碍了热量的传递。转子轴经过润滑油冷却后温度明显降低，其与润滑油的对流换热系数为616W/（m2·K）。轴承体上部由于润滑油的冷却作用，温度得到有效控制，而轴承体下部温度较高，最高温度达469.94℃。因此，对于密封环处温度的控制，重点在于轴承体下部。

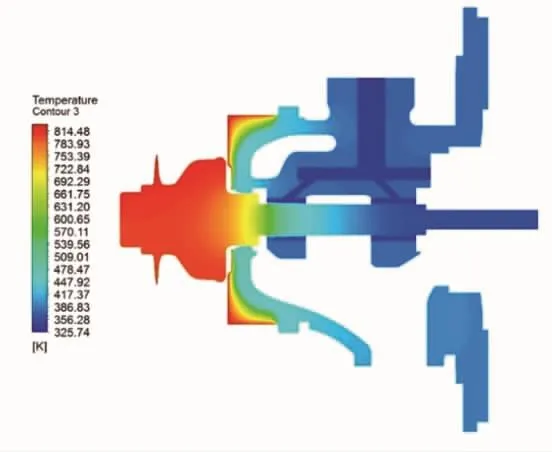
图7 轴承体yz平面切面温度分布云图

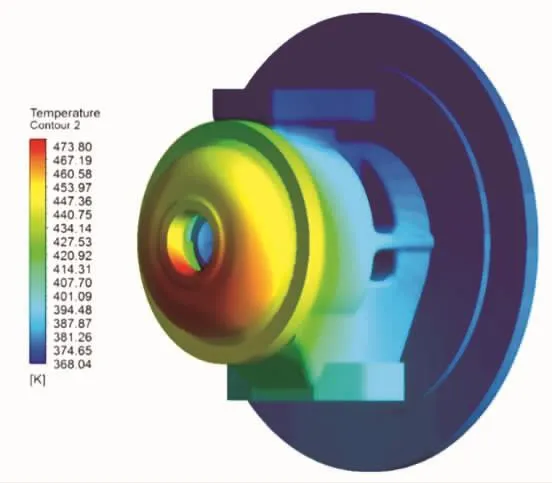
图8 轴承体外表面温度分布云图

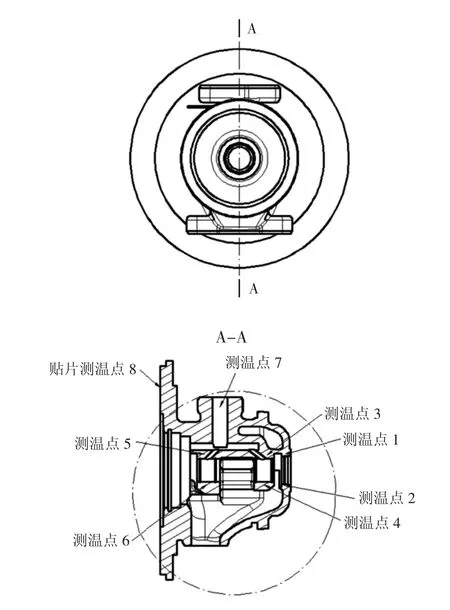
图9 测温点示意图

为了研究轴承体关键部位温度的变化情况，选取8个测温点进行分析，如图9所示。测温点1~8分别对应密封环上部、密封环下部、涡轮端轴承上部、涡轮端轴承下部、压气机端轴承上部、压气机端轴承下部、润滑油入口、压气机端壁面等。

通过仿真计算所得各测温点的温度随增压器转速的变化如图10所示。从图10可以看出，各测温点的温度随着转速升高而上升。密封环下部的温度高于上部，温差在24~35℃之间。随着转速增加，排气温度升高，密封环上下部测温点的温差有增大的趋势。在转速为110 000 r/min的工况下，密封环下部测温点的温度可达203.48℃。虽然低于理论温度限值230℃，但如果排气温度进一步升高，则存在超温的风险。轴承处温度较高部位在涡轮端轴承上部，最高温度为119.51℃，而涡轮端轴承下部及压气机端轴承处最高温度仅为102.53℃，温度较低。值得注意的是涡轮端轴承下部的温度低于压气机端轴承温度，这得益于该增压器轴承体良好的内部空腔设计。从图7可知，涡轮端轴承座仅通过上部与轴承体连接，接受来自涡轮端的热量，而轴承座其他部位与轴承体均无直接连接，并设有隔热空腔。隔热空腔的设计改变了热量的传递线路，使得来自涡轮端的热量大部分通过轴承体外壁面传至压气机端，而外壁面与大气接触，因此热量得以消散，传至压气机端轴承座时温度已降低到合理范围，大大缓解了涡轮端轴承处热量积聚的情况。

综合以上分析，该涡轮增压器轴承体的密封环上部、密封环下部及涡轮端轴承上部温度较高，存在一定的超温风险，而其它测温点的温度均能得到有效控制。

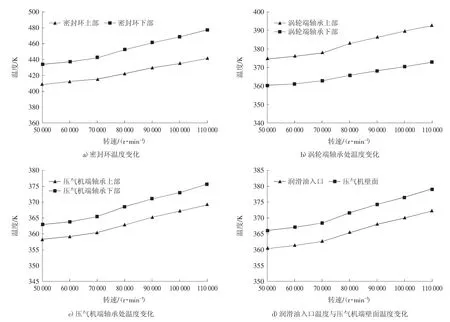
图10 测温点的温度变化曲线

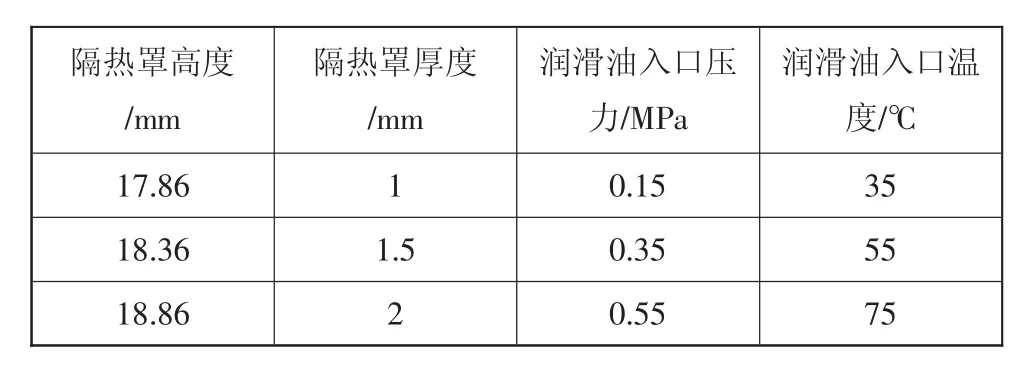
表3 因素水平表

图11 隔热罩结构参数标识

3 轴承体温度场显著影响因素分析及优化

在不对轴承体作几何结构改动的情况下，隔热罩作为阻隔涡轮端热量向轴承体传递的重要环节，与作为重要散热途径的润滑油一起构成了决定轴承体温度场的关键因素。

为了得到可能影响轴承体温度场的显著因素，选取隔热罩高度（A）、隔热罩厚度（B）、润滑油入口压力（C）、润滑油入口温度（D）等4个参数，每个参数选取3个水平，如表3所示。其中隔热罩结构参数标识如图11所示。设计基于L9（34）正交表的试验方案，研究和分析各参数对轴承体温度场的影响情况。基于极差分析，得到各影响因素的主次关系。

利用上述轴承体三维传热模型，对基于正交表的试验方案中各试验号进行仿真计算，选取存在超温风险的密封环上部、密封环下部以及涡轮端轴承上部等3个测温点的温度作为试验指标，得到正交试验结果。表4为密封环下部测温点处的试验结果。

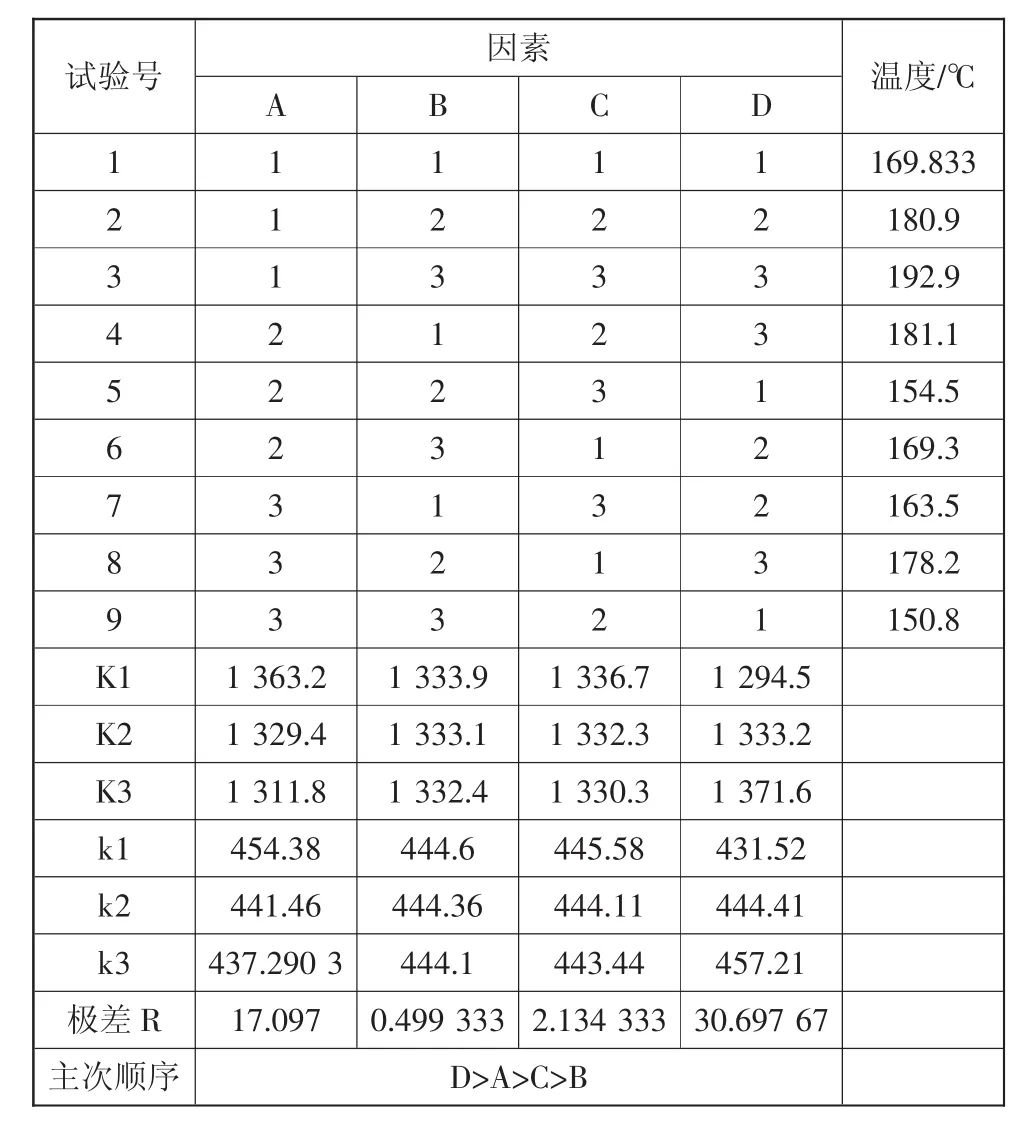
表4 密封环下部试验结果

对每个指标做极差分析可知，隔热罩高度与润滑油入口温度对涡轮增压器轴承体温度场分布影响性较大，其次是润滑油入口压力，隔热罩厚度影响最小。原因是隔热罩高度的改变实际上是增加了空气夹层的厚度；隔热罩厚度的改变实际上是增加了隔热罩金属材料的厚度。本文所用隔热罩材料为1Cr18Ni9Ti，在温度为100℃时，其导热系数为12.64W/（m·K），此时空气夹层导热系数为0.031 84W/（m·K），隔热罩导热系数为空气夹层导热系数的397倍，因此隔热罩高度的改变对于热阻的提高更为明显。润滑油温度的降低是通过提高壁面与冷却介质的温差来提高换热量，根据牛顿冷却公式，热流密度与温差成正比，因此效果明显。

综上所述，对于该增压器轴承体温度场而言，隔热罩高度与润滑油入口温度为显著影响因素。隔热罩高度越大，轴承体温度越低。因此，为了降低轴承体超温风险，应合理增加隔热罩高度。但在确定润滑油入口温度时，需考虑润滑油温度对轴承体温度场分布和增压器转轴摩擦功耗的综合影响。因为，润滑油温度降低虽然可降低局部温度，但润滑油粘度降低会引起转轴转动时的摩擦功耗增加。所以，需要进一步计算分析，确定合理的润滑油供给温度。

4 结论

1）在进行涡轮流体域仿真计算时，涡壳壁面为绝热的设置方式会导致低转速工况下等熵效率的仿真值略低于试验值。转速升高后，热量传递对等熵效率的影响不再明显。

2）轴承体温度场分布呈现由涡轮端向压气机端逐级递减的趋势，润滑油油道的分布以及轴承体内部涡轮端轴承座仅通过上部与轴承体连接的结构设计使轴承体下部温度略高于上部。容易在高负荷时出现超温现象的部位为密封环上部、密封环下部和涡轮端轴承等3处部位。

3）影响轴承体温度的关键因素为隔热罩高度和润滑油入口温度，增加隔热罩高度可降低轴承体内部发生超温的风险，润滑油入口温度的确定要综合考虑其温度对转轴摩擦功耗的影响。

1 张志永.汽油机瞬态工况燃烧特性的实验研究[D].长沙：长沙理工大学，2007

2 亓骥才.涡轮增压柴油机瞬态特性影响规律研究[D].上海：上海交通大学，2013

3 王俊，陶杰祥，李军.柴油机涡轮增压器使用注意事项[J].工程机械与维修，2011（9）：187

4 钱利东.柴油机废气涡轮增压器的使用与维护[J].农机使用与维修，2010（6）：81-82

5 朱大鑫.涡轮增压与涡轮增压器[M].北京：机械工业出版社，1992

6 赵汉中.工程流体力学[M].武汉：华中科技大学出版社，2011

7 H.K.Versteeg,W.Malalasekera.An introduction to computational fluid dynamics:The finite volumemethod[M].New York:Wiley,1995