液量平衡控制技术的研究

阳建华，何燕，马云燕，何春燕，秦梦

川北医学院附属医院 a.国资部；b.手术室；c.血透室，四川 南充 637000

引言

很多医疗设备特别是用于急救诊疗设备中常用到液体容量平衡技术[1-3]。在医院急救中心常用的全自动洗胃机内部，用到平衡进出胃的液量以保证洗胃的安全；在医院血液净化中心常用的血液透析设备内部用到新鲜透析液与废弃透析液间量的平衡技术；在有些压力传感器探测量的过程中用到液量平衡技术[4-7]。目前液体容量平衡技术机理很多是利用液体量的直接对等关系来设计技术结构，如平衡腔、平衡囊等均是一个机械性的容量测控技术，没有平衡过程中的动态比较，因此不能确保液量平衡均匀性，也就不能很好满足设备仪器性能要求，特别是医疗仪器设备在服务于患者过程中，更强调与人的生理和心理顺应性，所以精确稳定的液量平衡在提高仪器性能方面具有很多实际意义。

1 实验

1.1 实验器材

吸排泵（变压直流电源驱动，采用小功率蠕动泵）2只；硅胶管（透明、耐高温可达90℃）数米；单向滤芯（白色、透明，与硅胶管配套连接）数只；数字液体压力表（能与硅胶管配套连接，-1～+1 bar量程）；文氏流量计（可以直接显示流量数值）2个；精密称重秤（可以直接显示质量数值，量程5 kg）4台；直流电源（≥3道输出，5～36 V无级可调，输出总功率≥200 W）1台；空间足够大的调温绝热箱体一个（用于将实验平台放置在其内部）；纯净水或反渗透水1桶（≥20 kg）；另备小型塑料桶2只；NaHCO3干粉若干；精密秒表一只。

我们选用文氏流量计，考虑到文丘里管压力损失最低，有较高的测量精度，对流体中的悬浮物不敏感，可用于污脏流体介质的流量测量,特别适合医用废水的流量测量[8]。控制吸排泵运行时间来计量流量变化。

1.2 液量平衡模型

1.2.1 容积平衡

（1）容积平衡公式见公式(1)：

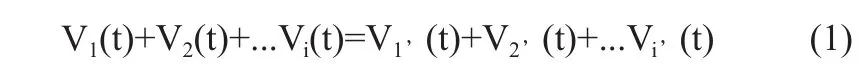
（2）容积平衡的机理：V1、V2、...Vi表示分别从不同路径进入系统的液体容积量大小；V1’、V2’、...Vi’表示分别从不同路径流出系统的液体容积量大小。i值大小是根据实际的流路系统需求选取，系统愈复杂则i值一般选择较大[9]。t是时间，参数V是时间t的函数。

（3）容积平衡模型图示，见图1。为了简化分析，我们选取t=2，即2进2出模型系统。

图1 容积平衡模型示意图

（4）容积平衡实验连接示意图，见图2。测试准备条件：实验室内空调温度设置为25℃±1℃；将图示的实验器材连接好后整体放置在一个空间足够大的调温绝热箱体里，箱体透明，可观察各表的示值；流体介质是：溶剂是反渗透纯净水，溶质是NaHCO3，本次实验不用甘油与水混合后测试；P1、P2接变频驱动模块电源，以便泵转速调节，调节P1、P2转速，使得Pd示值为500 mmHg或者300 mmHg[10]。

图2 容积平衡实验连接示意图

1.2.2 质量平衡

（1）质量平衡公式见公式(2)：

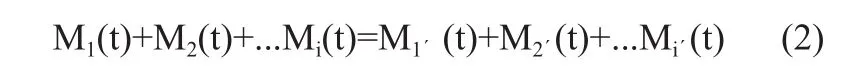
（2）质量平衡机理：M1、M2、...Mi表示分别从不同路径进入系统的液体质量大小；M1´、M2´、...Mi´表示分别从不同路径流出系统的液体质量大小。t值大小是根据实际的流路系统需求选取，系统愈复杂则t值一般选择较大[11]。t是时间，参数M是时间t的函数。

（3）质量平衡模型示意图，见图3。为了简化分析，我们选取i=2，即2进2出模型系统。

图3 质量平衡模型示意图

（4）容积平衡实验连接示意图，见图4。测试准备条件与容量平衡测试条件一样。

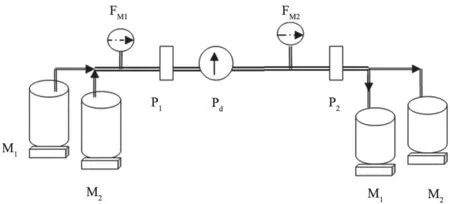
图4 质量平衡实验连接示意图

2 结果

我们设计的上述实验平台，是在一定液流温度、液流压力下液体流量与液体密度、液流截面大小间的关系。以1 min为一次测试累计时间，测试分两种情况（容积变化测试、质量变化测试），每种情况测试4个时间段的变化数据：t0-t1期间，两道进出管径大小一致，测试累计时间1 min；t1-t2期间，仅2道进出管径缩小至一半，测试累计时间1 min；t2-t3期间，仅1道进出管径缩小至一半，测试累计时间1 min；t3-t4期间，仅1道进出管径缩小至三分之一，测试累计时间1 min。

2.1 容积平衡模型实验平台测试

在测试条件为T（绝热调温室的温度）=37℃，P（Pd表示值）=500 mmHg，我们进行了如下两种情况的测试。

（1）当V1、V2里均装纯净水，V1´、V2´为空，先预备运转使管路内充满水，记录开始时间从t0起。在t1-t2期间内，改变从V2进液体的口径大小和V2´出液体口径的大小（1/2口径）；在t2-t4期间内，改变从V1进液体的口径大小和V1´出液体口径的大小（1/2、1/3）。具体测试数据，见表1。

（2）当V2里均装纯净水，V1里装10%的NaHCO3水溶液，其它条件同上，记录开始时间从t0起。在t1-t2期间内，改变从V2进液体的口径大小和V2´出液体口径的大小（1/2口径）；在t2-t4期间内，改变从V1进液体的口径大小和V1´出液体口径的大小（1/2、1/3）。具体测试数据，见表2。

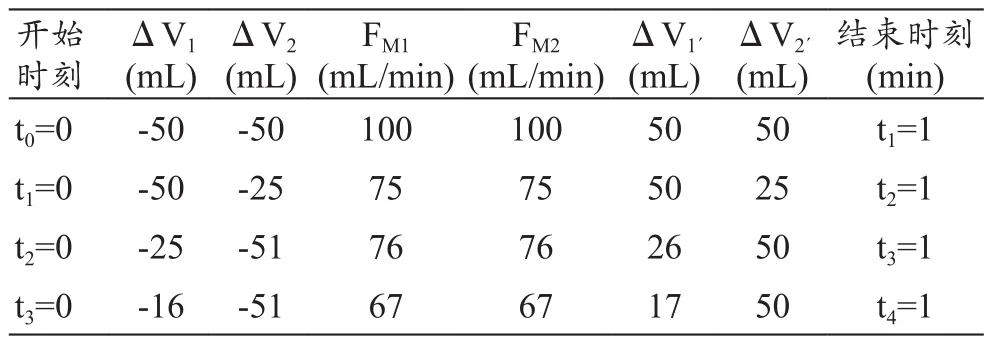
表1 纯净水条件下采用容积平衡模型实验平台测试的数据记录表（P=500 mmHg）

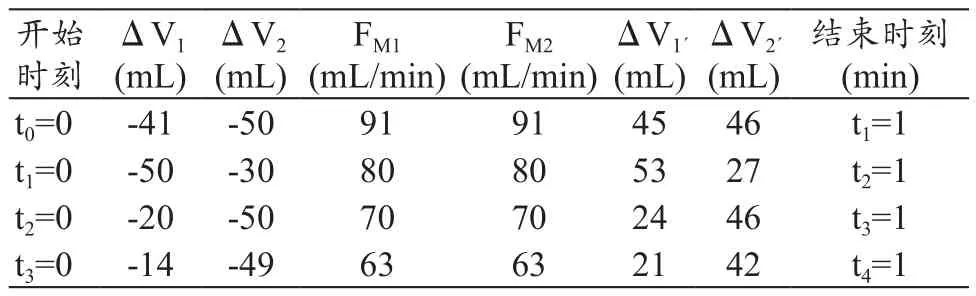
表2 纯净水和10%的NaHCO3条件下采用容积平衡模型实验平台测试的数据记录表（P=500 mmHg）

同理，在测试条件为T（绝热调温室的温度）=37℃，P（Pd表示值）=300 mmHg时，我们进行了如下两种情况的测试。

（1）V1、V2里均装纯净水，为空，先预备运转使管路内充满水，记录开始时间从t0起。在t1-t2期间内，改变从V2进液体的口径大小和V2´出液体口径的大小（1/2口径），在t2-t4期间内，改变从V1进液体的口径大小和V1´出液体口径的大小（1/2、1/3）。具体测试数据，见表3。

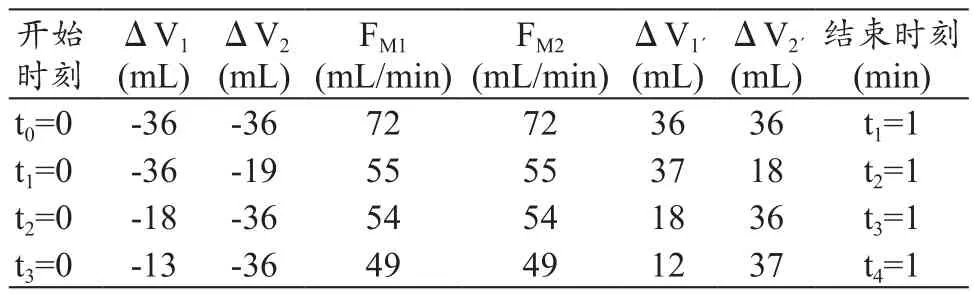
表3 纯净水条件下采用容积平衡模型实验平台测试的数据记录表（P=300 mmHg）

（2）当V2里均装纯净水，V1里装10%的NaHCO3水溶液，其它条件同上，记录开始时间从t0起。在t1-t2期间内，改变从V2进液体的口径大小和V2´出液体口径的大小（1/2口径）；在t2-t4期间内，改变从V1进液体的口径大小和V1´出液体口径的大小（1/2、1/3）。具体测试数据，见表4。

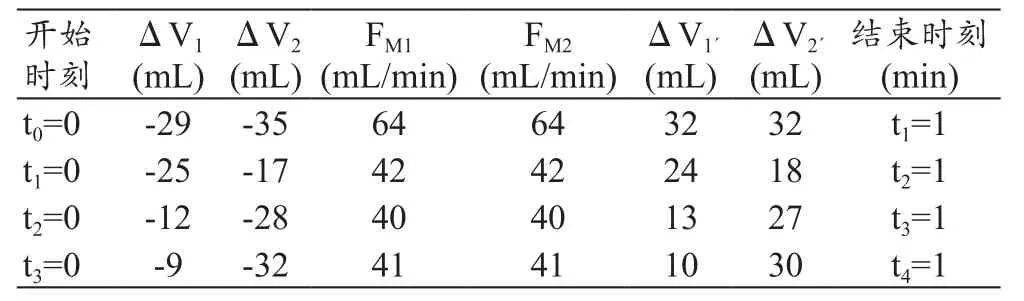
表4 纯净水和10%的NaHCO3条件下采用容积平衡模型实验平台测试的数据记录表（P=300 mmHg）

本实验数据是在配合使用各种管径胶管下满足表中条件测出的。从上表数据可以看出：① 采用纯净水作为流动液体，前后容量变化总量基本相等（即ΔV1+ΔV2=ΔV1´+ΔV2´）， 并与 FM1、FM2示 值吻 合 ；但是，在流体压力一定情况下FM1、FM2示值与进液口管径大小有关，这符合流体力学原理；② 采用混合溶液吸入作为流动液体，前后容量变化总量基本相等（即ΔV1+ΔV2=ΔV1´+ΔV2´），并与 FM1、FM2示值差异不明显；但是，输出对应通道变化量比较有差异，并且比较明显，如ΔV1、ΔV1´间和ΔV2、ΔV2´间的误差达到10%以上，且随流体通道压力增加而误差率会变大。

2.2 采用质量平衡模型实验平台测试

在测试条件为T（绝热调温室的温度）=37℃，P（Pd表示值）=500 mmHg，我们进行了如下两种情况的测试。

（1）M1、M2里均装纯净水，M1´、M2´为空，先预备运转使管路内充满水，记录开始时间从t0起。在t1-t2期间内，改变从M2进液体的口径大小和M2´出液体口径的大小（1/2口径）；在t2-t4期间内，改变从M1进液体的口径大小和M1´出液体口径的大小（1/2、1/3）。具体测试数据，见表5。

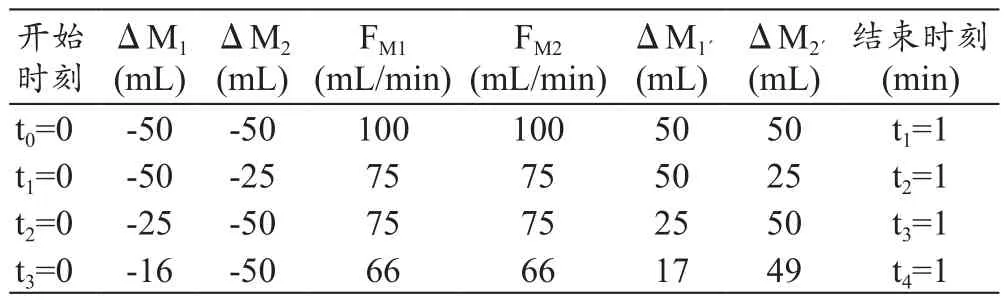
表5 纯净水条件下采用质量平衡模型实验平台测试的数据记录表（P=500 mmHg）

（2）M2里均装纯净水，M1里装10%的NaHCO3水溶液，其它条件同上，记录开始时间从t0起。在t1-t2期间内，改变从V2进液体的口径大小和V2´出液体口径的大小（1/2口径）；在t-t期间内，改变从V进液体的口径大小和241出液体口径的大小（1/2、1/3）。具体测试数据，见表6。

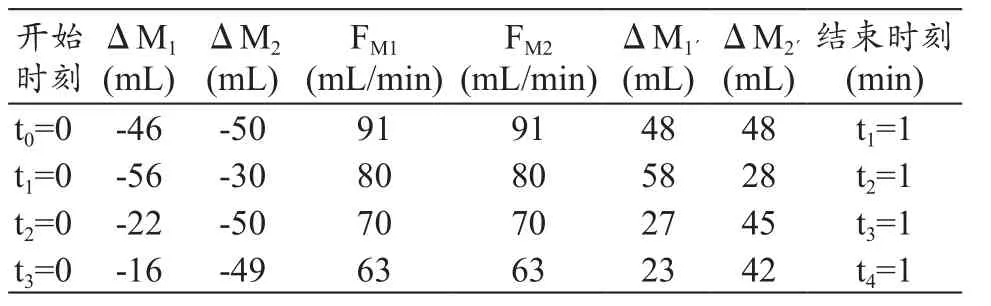
表6 纯净水和10%的NaHCO3条件下采用质量平衡模型实验平台测试的数据记录表（P=500 mmHg）

同理，在T（绝热调温室的温度）=37℃，P（Pd表示值）=300 mmHg时，我们进行了如下两种情况的测试。

（1）M1、M2里均装纯净水，M1’、M2’为空，先预备运转使管路内充满水，记录开始时间从t0起。在t1-t2期间内，改变从M2进液体的口径大小和M2’出液体口径的大小（1/2口径）；在t2-t4期间内，改变从M1进液体的口径大小和M1’出液体口径的大小（1/2、1/3）。具体测试数据，见表7。

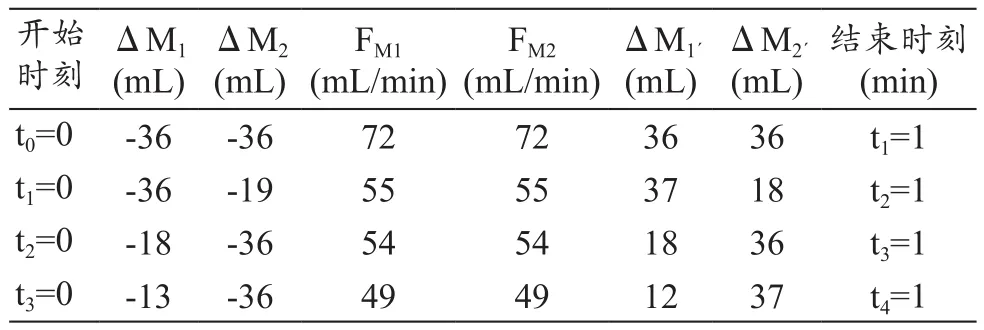
表7 纯净水条件下采用质量平衡模型实验平台测试的数据记录表（P=300 mmHg）

（2）M2里均装纯净水，M1里装10%的NaHCO3水溶液，其它条件同上，记录开始时间从t0起。在t1-t2期间内，改变从M2进液体的口径大小和M2´出液体口径的大小（1/2口径）；在t2-t4期间内，改变从M1进液体的口径大小和M1´出液体口径的大小（1/2、1/3）。具体测试数据，见表8。

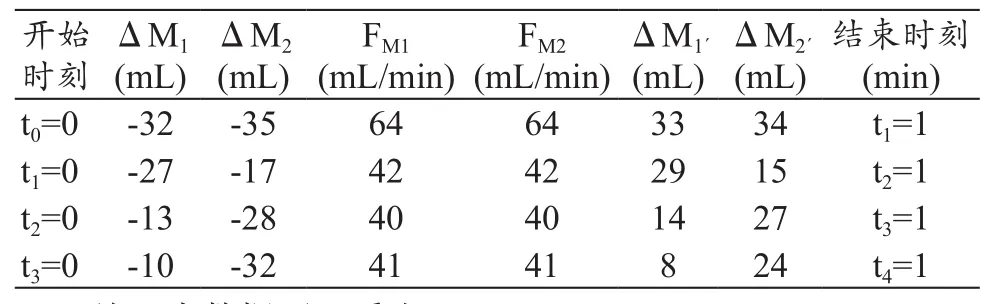
表8 纯净水和10%的NaHCO3条件下采用质量平衡模型实验平台测试的数据记录表（P=300 mmHg）

从上表数据可以看出：

（1）采用纯净水作为流动液体，前后质量变化总量基本相等（即 ΔM1+ΔM2=ΔM1´+ΔM2´），并与 FM1、FM2示值吻合；按照纯净水密度为1g/mL，质量大小和体积大小相当；同样，流体压力一定情况下FM1、FM2示值与进出液口管径大小有关，口径大FM就大，符合流体力学原理。

（2）采用混合溶液吸入作为流动液体，前后质量变化总量基本相等（即 ΔM1+ΔM2=ΔM1´+ΔM2´），并与 FM1、FM2示值差异明显，这主要是因为FM示值反映的是体积流量大小而非液体质量大小；输出对应通道变化量值比较也有明显差异，如ΔM1与ΔM1´间误差率达到20%以上，而ΔM2与ΔM2´间的误差率达到30%以上；随流体通道压力增加误差率会变大，如在500 mmHg就比在300 mmHg情况下对应通道误差率大。

从上述两种模型的实验数据分析结果可以看出，在温度不变的情况下，流体液量体积的平衡和分配与流体液量质量的平衡和分配是不一样的，液量的变化与液流压力变化、液体密度变化、液流管径大小密切相关。表中数据没有考虑仪表示值误差带来了不准确性。根据流体力学原理，可以肯定的是，对应通道的液量平衡与分配会受到管径大小、液体溶质浓度即密度、温度、流体压力以及系统复杂程度的影响。

实际情况下等质量的同种混合液体容积会受温度T、压力P以及混合比R的变化而产生变化。我们最关心的是实现液体质量的动态变化的平衡性。正如我们实验初衷是找出 M1与 M1´、M2与 M2´、V1与 V1´、V2与 V2´等通道的液量是否能保持平衡一样，在很多医疗设备中就是要找出这两点间平衡差，以确定我们的治疗效果。如透析机超滤量就是依靠多次的平衡来确保超滤的精准性。

这个保持液量平衡的机理可用公式表述为m1=m2+a，m1为前质量即可以是进入各道的液量总和，m2为后质量即可以是流出各道的液量总和；a为实际处理过程中质量平衡差，a与时间长短、系统设置、个体差异有关；在很多医疗仪器中，a是来自于人体诊疗过程中，通过测试m1与m2之间的差得到我们所需要的a值[11-14]。

3 结论

本实验目的是通过液量传输过程中的体积和质量变化规律来研究液量平衡控制技术，也就是要精确地找到那个a值。从实验数据结果按照经典控制理论原理，实现液量平衡控制的技术本质在于消除系统的误差、提高系统的精密性。因此，下列各点指出的技术参数务必采用可靠实用的控制方法来提高系统精度以减少误差。

（1）系统中有P1、P2吸排泵，它的主要作用是维持要求的液流压力Pd。把探测Pd偏离值转换成反馈信号去控制P1、P2吸排泵的驱动电压占空比，只有精确的驱动电压占空比才可以实现稳定的Pd值。

（2）m1=m2+a中的a值是我们期望的效果。它的精确与否取决于系统的科学设计与精密监测，仅仅依靠体积变化来折算成a值，是粗糙而不准确的。因此，先判断体积是否平衡再判断质量是否平衡对平衡控制技术研究来说是行之有效的。

（3）保持系统在稳定的温度环境下工作，流路口径值精确，液流在不压缩膨胀情况下稳定流动。这样系统运行的误差就会大大减小。

从以上三点来看，压力、温度、流体密度、流体质量、流体体积等参数是本系统研究的几个重要物理量，它们均是与时间t存在关系的。因此，液量平衡控制技术实现注意点有以下：考虑整个液流系统的温度恒定性如何即温差较大还是较小；考虑整个液流系统的压力变化较大还是较小；考虑混合液流的理化特性的变化过程是否复杂即考虑是否仅有物理变化还是会发生化学变化等情况；考虑液流速率的变化与质量分配的变化，容积的变化与质量的变化等问题[15]。

如果将改变液体质量的有关物理因素考虑进去，就可实现质量平衡新的精准模型。当某个条件（温升和暴露）的改变引起了液体本身的化学反应并形成了气体而挥发，那么液体体积与质量必然会随时间t发生变化。物理化学原理告诉我们，任何混合性物质在温度、压力以及新物质的作用下或者有物理变化或者有化学变化，特别是多种物质含量复杂的混合液体这种可能性更大。物理实验中常用天平测定质量，利用杠杆原理实现精确平衡差，这是因为质量反映的是重量的变化，受温度、压力及液体混合比差异等因素影响相对较小[16]。因此，真正的液量平衡模型必须建立在容积和质量双重平衡机制下，仅仅依靠液体容积参数的监测来判断平衡特性是不准确和可靠的。

有了这些经验后，按照实际系统功能的需要，针对泵的精密转速、流量计（秤）检测输出数据的精准控制及电路的EMC（电磁兼容）研究是该液流系统机电控制工程技术研究的必要部份，也是研究液量平衡控制技术的重要内容。

[参考文献]

[1] 李宾中.医学物理学[M].北京:科学出版社,2010.

[2] 胡汉才.单片机原理及其接口技术[M].北京:清华大学出版社,1995.

[3] 朱文立.电磁兼容设计与整改对策及案例分析[M].北京:电子工业出版社,2012.

[4] 姜远海.临床医学工程技术[M].北京:科学出版社,2009.

[5] 徐彤.最新电子电路速查手册[M].九江:江西科学技术出版社,1997.

[6] 杨子彬.生物医学工程学[M].黑龙江:黑龙江科学技术出版社,2000.

[7] 舒辰慧.物理学[M].北京:人民卫生出版社,2003.

[8] 胡新珉.医学物理学[M].7版.北京:人民卫生出版社,2008.

[9] 潘志达.医学物理学[M].北京:科学出版社,2007.

[10] 祝之光.物理学[M].3版.北京:高等教育出版社,2009.

[11] 邓玉林.生物医学工程学[M].北京:科学出版社,2007.

[12] 陈熙谋.光学 近代物理[M].北京:北京大学出版社,2007.

[13] 严宗毅,许世雄,章克本.流体力学(下)[M].2版.北京:高等教育出版社,2006.

[14] 刘晓波.管道流体流量测量实验系统构建与分析[D].太原:中北大学,2014.

[15] 何岳.CosmosFloworks在管道流体分析中的应用[J].山东工业技术,2014,(17):39.

[16] 郝柏林.物理学和生物学(下)[J].物理,2003,32(6):353-359.