M序列反馈函数多项式表示的快速构造方法

关杰，周琮伟

（解放军信息工程大学三院，河南 郑州 450001）

1 引言

一个n级移位寄存器至多产生周期为2n的序列，通常称达到最大周期2n的序列为M序列，又叫De Bruijn序列。关于LFSR的圈结构已经可以完全刻画，并且知道最大周期的2n-1的序列由其特征多项式为二元域上的本原多项式产生，此时，称周期为2n-1的序列为m序列。相较于m序列，M序列有着更好的线性复杂度和自相关性质，一直以来其构造问题是序列密码理论的研究热点。由于NFSR的圈结构没有较好的刻画手段，故其构造的经典方法一直以来局限于图论的反树和因子关联图法[1]，小项表示的圈剪接筛法[2]和由一个M序列通过对称[3]、派生[4]和递归[5]等得到一类M序列。近期，国外学者关于M序列的构造主要有“改进版”的Martin算法[6]以及关于D-同态递归构造的最新研究成果[7]。而国内学者关于M序列构造的新思路和研究主要有“编织法”[8]，利用复合函数所代表的寄存器因子关联图的研究构造M序列[9～13]以及针对大级数的并圈构造[14]。以上这些构造方法大致可以分为两类，即同级直接生成的“并圈法”以及小级数递归生成大级数的“递归法”。但是“并圈法”生成的M序列往往需要大量的统计、判断和检验，并且得到的M序列往往是以小项表示；而“递归法”往往得到的M序列个数较少且M序列往往与小级数的初始序列具有较大相关性。

因此，针对以上M序列在实际构造中存在的问题，本文提出了一类可以实际应用，且以多项式表示的M序列反馈函数的快速构造方法。

2 预备知识

以下是本文用到的定义和符号说明。

Gf：以f为反馈函数的n级移位寄存器的状态图。

对偶变换D：设为f产生的GF(2)上任意一条周期为T的序列，令“+”为GF(2)上的加法运算，则aT+1,…)。

对称变换R：

组合变换RD：a1+1,… )。

Ai：f0(x2,…,xn)中所有i(0 ≤i≤n-1)次项的集合为Ai，特别地，零次项为 1以及最高次项为x2…xn。

常见的反馈函数有2种表示方法，即小项表示和多项式表示。在实际应用中，更实用的是用多项式表示的反馈函数，因为利用多项式表示的反馈函数其构造M序列无论从软件和硬件实现的角度都更为方便快捷。文献[15]给出了圈结构不含枝即非奇异的n级反馈函数，其用多项式表示3种函数变换的对应表达式。

定理 1[15]设非奇异n级反馈函数的多项式表示为f=x1+f0(x2,… ,xn)，若分别用Df、Rf和RDf表示以D(Gf)、R(Gf)和RD(Gf)为状态图的n级移位寄存器反馈反馈函数，则

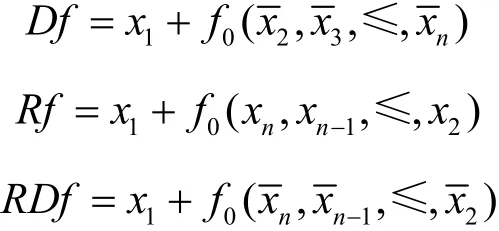
1946年，De Bruijn从图论的角度证明了产生M序列的非线性移位寄存器的个数等于而非奇异移位寄存器的个数恰好等于但是至今人们都无法证明M序列的非线性移位寄存器以2n的长度划分了整个非奇异移位寄存器，即猜想若将整个非奇异移位寄存器对应的反馈函数看作一个群，而M序列的反馈函数可以看作是个数为2n的陪集的代表元。20世纪80年代，高鸿勋[16]在以圈剪接筛法的基础上提出了一个非奇异反馈函数为M序列反馈函数的充要条件，但对于生成全部n(n≥ 5)级M序列来讲没有实际意义。

本文直接引用文献[15]中关于M序列反馈函数多项式表示的一个必要条件来说明随机寻找到一个M序列反馈函数的数据复杂度。

引理 1[15]在M序列反馈函数f0的多项式表示中，有以下性质。

1) 最高次项x2…xn这一项一定出现。

2) 项数一定是奇数。

3) 1这一项一定出现。

4) 一次项x2,…,xn不能全部出现。

由于考虑将1和x2…xn这2项排除，则剩余可能出现的项的个数即为 2n-1- 2 。在此基础上将2n-1- 2 种可能出现的项进行一个分类，即定义Ai(1 ≤i≤n-2)，则可能产生M序列反馈函数的个数为 22n-1-2。又因为项数一定是奇数，则可能产生M序列的反馈函数的个数可以降到 22n-1-3。如果从线性项x2,…,xn不能全部出现的角度考虑，则可能产生M序列反馈函数的个数为假设M序列的反馈函数服从均匀分布，则实际利用引理 1寻找到一个M序列反馈函数的数据复杂度约为O(2n-3)。

文献[15]给出了利用对偶变换D、对称变换R和组合变换RD构造M序列的结论。如引理2所示。

引理2[15]f是M序列的反馈函数，则Df、Rf和RDf也是M序列的反馈函数。当n≥ 3 时，f≠Df、f≠Rf；当n为偶数时，f、Df、Rf、RDf这4个函数两两互异。

由于在实际应用中并不需要生成全部的M序列反馈函数，更多的时候是需要生成具有某些构造特点的多项式表示的反馈函数。本文的工作即是利用由m序列构造M序列反馈函数的结构特性，经上述 3种函数变换得到一类M序列反馈函数多项式表示的快速构造方法，为了更好地说明对偶变换D、对称变换R以及组合变换RD在构造M序列反馈函数中的应用，接下来，给出2个关于m序列的结论。

3 由函数变换证明的2个结论

本文由函数变换发现了m序列个数及其特征多项式的一些性质，并从另外一个角度证明了如下结论。

引理3[17]当n≥ 3 ，总为偶数。

证明 当n≥ 3 时，由引理 2知，Rf形成的必然是一条新的m序列，则f≠Rf，因此，由Rf形成的特征多项式必然异于f的本原多项式，而二元域上的本原多项式的总数为因此，当必然为偶数，证毕。

定理2 当n为偶数且n≥ 3 时，不存在形式为的本原三项式。

证明 当n为偶数且n≥ 3 时，对于特征多项式

4 函数变换及函数派生在构造M序列反馈函数中的应用

4.1 函数变换在构造M序列反馈函数中的应用

在实际构造M序列的过程中，人们很自然地考虑从m序列出发，即考虑在m序列长度为n-1的0游程中添加一个0得到M序列，这也符合对M序列的游程统计。这种情况构造的M序列反馈函数其实是在m序列的反馈函数表达式中添加一个小项当然将小项表示转化为多项式表示中，发现得到的M序列反馈函数满足引理1的性质，考虑该M序列反馈函数的对偶函数时，其对偶函数也应该为M序列的反馈函数，据此给出了一类M序列反馈函数f快速构造的多项式表示的形式，即形式1。

形式 1 在m序列的反馈函数q的基础上添加这2项，即

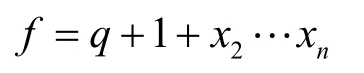
容易看出，具有形式1的多项式表示的反馈函数f满足引理1，从而可以推出m序列的项数为偶数项，否则与f中出现1这一项相矛盾。

同时考虑对称函数Rf和RDf，当n≥ 3 ，由f对称所形成的必然是新的一条M序列，所以势必由f可以得到一个新的满足M序列的反馈函数Rf，观察其结构可知，仍然是在m序列的反馈函数上添加 1,x2…xn这2项，其与引理3的结论是相对应的，同理可得RDf与Df具有相同结构。据此，可以快速构造个M序列反馈函数。

如果本文将x1,1,x2…xn这3项单列，指出任意由形式1构造的M序列反馈函数的对偶函数Df具有定理3的形式。

定理3 任意由形式1构造的M序列反馈函数f的对偶函数Df具有以下形式。

1) 包含x1,1,x2…xn这3项。

2) 包含f在集合Ai(1 ≤i≤n-2)中所有未出现的项。

证明 由于f=q+1+x2…xn=x1+f0(x2,…,xn)，则由定理1知，Df包含项，其多项式展开式中包含f0(x2,…,xn)中所有i(1 ≤i≤n-2)次项的集合为Ai以及 1,x2…xn。

由于f0(x2,…,xn)中的线性项共有奇数项，故Df一定包含x1,1,x2…xn这3项，且其余项为f在集合Ai(1 ≤i≤n-2)中所有未出现的项，故式(1)和式(2)得证。证毕。

为方便理解，本文给出定理3的一个实例。

例1 当n= 4时，f=x1+1+x2x3x4+x4，下面给出Df。

由于原函数在Ai(1 ≤i≤2)中未出现的项有

x2,x3,x2x3,x2x4,x3x4，因此

同时，发现Df+f中的函数项即是集合Ai(1 ≤i≤n-2)中所有出现的 2n-1- 2 项，因此，可以立即得到推论1。

推论1对于任意由形式1构造的M序列反馈函数f和Df，g为任意M序列反馈函数，则f+Df+g具有如下形式。

1) 包含x1,1,x2…xn这3项。

2) 包含g在集合Ai(1 ≤i≤n-2)中所有未出现的项。

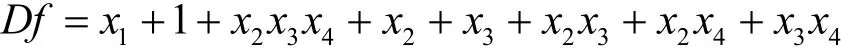
4.2 函数派生在M构造序列反馈函数中的应用

根据之前对基于由m序列构造M序列的分析可知，如果仅从A1选择奇数项，只能是形式1构造出的个M序列反馈函数f，于是，设想以此为基础加上若干偶数项可以构造新的M序列反馈函数。本先给出文献[15]中一个关于函数派生的结论，文献[15]中的证明比较烦琐，下面，利用文献[18]中状态图的连线与交点的赋值定义给出简化证明。

定理4[15]若f是n级M序列的反馈函数，则以下2个式子也是M序列的反馈函数。

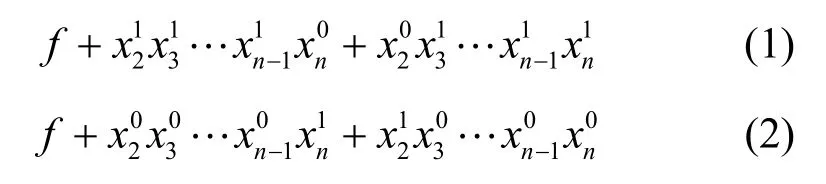
证明 文献[18]指出，对于Gf状态图，任一2对共轭状态的连线的交点的赋值和指的是加上2个n- 1 维的小项其中，与分别是2对共轭状态。由圈剪接的思想[15]可知，f加上赋值和也是M序列的反馈函数。而2对共轭状态的连线要相交，必然在Gf中一对共轭状态之间有另一对共轭状态的其中一个。对于状态(0,0,1,…,1,1)来说，若其后继状态为(0,1,1,…,1,0)，由于((0,1,1,… ,1),(1,1,… ,1 ,1))这条弧必然存在，则状态(0,1,1,…,1)的先导必然为(1,0,1,1,…,1)，且同时(1,1,…,1,1)的后继必然为(1,1,…,1,0)，故形成这样一条长弧((0,0,1,…,1,1),(0,1,1,…,1 ,0),…,(1 ,0,1,1,…,1),(0,1,1,…,1),(1,1,…,1,1),(1,1,…,1,0))，则说明共轭状态(0,0,1,…,1,1),(1,0,1,1,…,1)和(0,1,1,…,1,0),(1,1,…,1,0)的连线必然相交；若其后继状态为(0,1,1,…,1)，则状态(0,1,1,…,1,0)的先导必然为(1,0,1,1,…,1)，故形成这样一条长弧((1,0,1,1,…,1),(0,1,1,…,1,0),…,(0,0,1,…,1,1),(0,1,1,… ,1),(1,1,…,1,1),(1,1,…,1,0))，则说明共轭状态(0,0,1,…,1,1),(1,0,1,1,…,1)和(0,1,1,…,1,0),(1,1,…,1,0)的连线必然相交。综上可知也是M序列的反馈函数。同理可证也是M序列的反馈函数，证毕。

下面，利用定理4的结论，给出了新的M序列反馈函数的4种形式

本文首先利用定理4的式(1)，即f是任意以形式 1构造的M序列反馈函数，则也是M序列反馈函数。

由此，可将f′描述成以下多项式表示的形式，即形式2。

形式 2 在形式 1生成的f基础上添加这2项，即

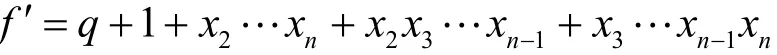
而此时的f′正好满足从A1选择奇数项，An-2选择偶数项。同时，考虑Rf′和Df′，易知Rf′还是属于与f′相同的一类M序列反馈函数，而

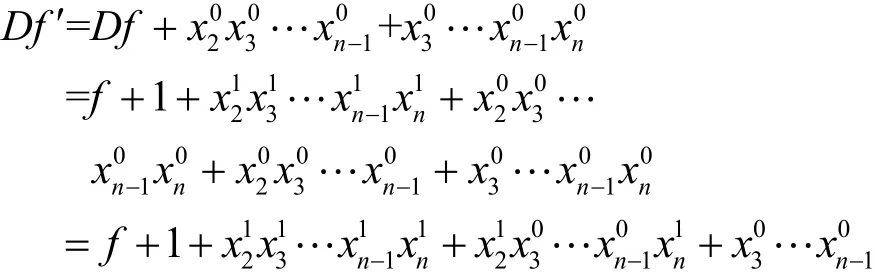
因此，Df′还可以描述成以下多项式表示的形式，即形式3。

形式 3 在m序列的反馈函数的基础上添加转化成多项式表示后，即在形式1生成的f基础上添加Aj(1 ≤j≤n-2)中排除后剩余的项。

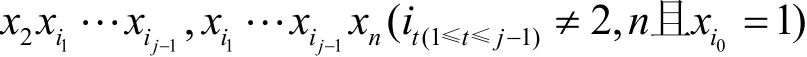
易知，当n＞ 3 时，Df′与f,Df不同。据此可以快速构造个M序列反馈函数，分别是f,Df,f′,Df′。

接下来，再次利用定理4的式(2)，即f是M序列反馈函数，则

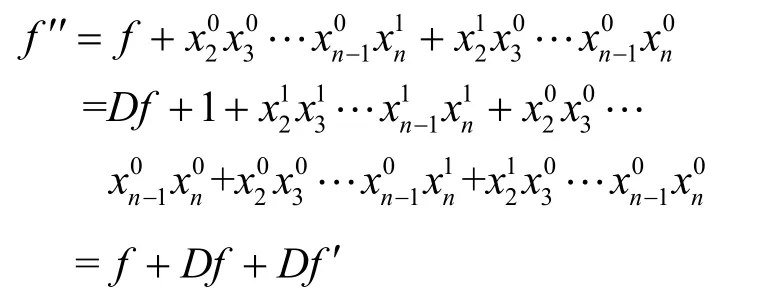
也是M序列反馈函数。若考虑此时的Rf′和Df′，则由f′的结构可知，Rf′还是属于与f′相同的一类M序列反馈函数。当n≥ 5 时，以及f′就与f,Df,f′,Df′不同。此时根据推论1，f′,Df′还可以描述成以下多项式表示的形式，即形式4。

形式4 除了有公共的x1,1,x2…xn这3项外，其余项为Df′,f′在集合Ai(1≤i≤n-2)中所有未出现的项。

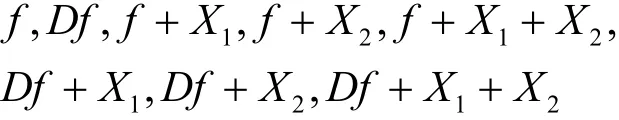
对于这类M序列反馈函数考虑函数之间相等的情况时，仅可能是f+X2=Df+X1与f+X1=Df+X2，此时的f与Df的小项表示必然是仅有一项不同，且不同的项为X2和X1，剩余的项必然是成对的互为对偶的项。因此，考虑到函数之间相等的情况是可能存在的，但出现的概率和个数较少，所以实际上这类方法可以构造约个M序列反馈函数。最后，可以用图1来总结这类快速构造方法生成的M序列反馈函数，其中，

4.3 一类M序列反馈函数的快速构造算法

为了说明这类M序列的构造方法可以在实际中快速生成以多项式表示的反馈函数，本文给出算法形式，如算法1所示。该算法分为离线和在线阶段，并且为了存储以多项式表示的反馈函数，将Ai(0 ≤i≤n-1)中的每一元素对应到n-1维的二元数组向量构成的集合

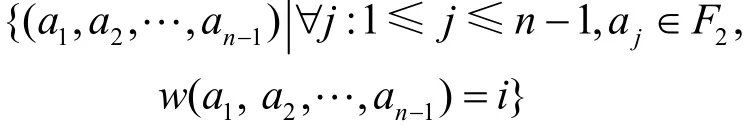
例如，常数1对应向量(0,…,0)，x2对应向量(1,0,…,0)，x2…xn对应向量(1,…,1)，CBA表示集合A在B中的补集。

算法1 一类M序列反馈函数的快速构造算法

离线阶段

对于给定级数n(n≥ 5)时，以向量形式存储Ai(0 ≤i≤n-1)中所有元素，并记全体n-1维的二元向量集合为U。对于给定的m序列的反馈函数，给出其线性项在A1中的向量集合Q，则在在线阶段只需求出M序列反馈函数中f0的对应向量集合，将集合中元素相加再加上x1，即可得到M序列反馈函数。

在线阶段

Step1 输入n级m序列的反馈函数中线性项的向量集合Q。

Step2 以形式1表示的M序列反馈函数中f0的对应向量集合F0为

Step3 以定理 3表示的M序列反馈函数中Df0的对应向量集合DF0为

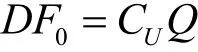
Step4 以形式2表示的M序列反馈函数中f0′的对应向量集合F0′为

Step5 以形式 3表示的M序列反馈函数中Df0′的对应向量集合DF0′为

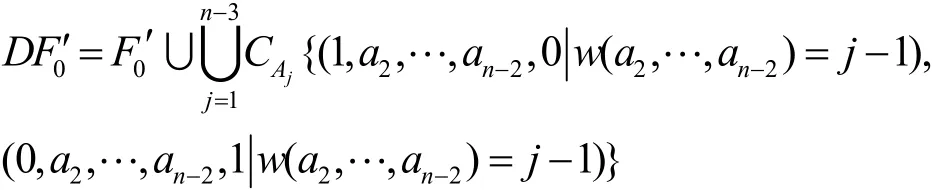
Step6 以形式 4表示的M序列反馈函数中f0′,Df0′的对应向量集合F0′,DF0′为

Step7M序列反馈函数中f0+X1+X2,Df0+X1+X2的对应向量集合为

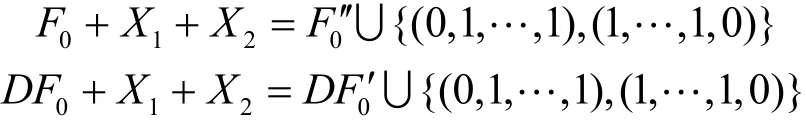
图1 一类M序列反馈函数的快速构造算法

分析该算法可知，由于离线阶段存储了所有多项式以次数为序的项数集合，存储复杂度即为则在线阶段，对于求一个给定集合在有序集合中的补集，只需要遍历输出该有序集合的部分元素即可，因此，时间复杂度为O(2n-1)。对比直接利用“并圈法”得到的以小项表示的M序列反馈函数，在其转化成多项式表示上所需要的时间复杂度将大大降低。同时，本文也是首次给出以多项式表示的M序列反馈函数的构造算法，下面，本文将简要分析该算法给出的这类M序列反馈函数的重量性质。

5 新的M序列反馈函数的重量性质

由于M序列反馈函数的结构总可以表示成，因此，M序列反馈函数的重量指的是f0的重量或f0小项表示的项数，即为w(f0)。在文献[15]给出了M序列小项表示的反馈函数的一个必要条件，有以下结论。

定理5[15]当n≥ 3 时，对于Z(n)- 1 与

之间的一切奇数都有以这奇数为重量的M序列反馈函数存在，其中，

根据定理5，实际上，本文限制了w(f0)的取值，并且w(f0)的取值是M序列反馈函数在实际应用中的重要参考指标，因此，接下来，考虑快速构造方法生成的M序列反馈函数的重量w(f0)。

首先，可以合理限定m序列的反馈函数为二项式，即表示为x1+xi，则通过形式1生成的M序列反馈函数f0=xi+1+x2…xn转化成小项表示后，其项数为w(f0)=2n-2+1 。当n较大时，Z(n)和Z∗(n)都远远小于2n-2，因此，w(f0) 的取值大概在重量区间的中间。由于函数变换不改变w(f0)的取值，以及这种函数派生方式重量的增减幅度为2或4，因此，新的M序列反馈函数w(f0)为以下取值之一：

其次，考虑m序列的反馈函数为四项式，即在二项式的基础上添加2个线性项。由于w(f0)从另一个角度可以看成f0=1的n-1维向量个数，新添加的2个线性项的取值（即该线性项等于0或1）使f0=1的情况个数与原有二项式比较不变，因此，此时n-1维向量满足f0=1的个数不变，即此时通过形式 1生成的M序列反馈函数的w(f0)取值为以此类推，通过形式1生成的M序列反馈函数w(f0) 取值为 2n-2+1[19]，此时，新的M序列反馈函数w(f0)为以下取值之一：

综上所述，可以得到以下结论。

结论M序列反馈函数f（其中，f为图 1所示的8类M序列反馈函数）的重量w(f0)的取值必然在以下集合中：

6 结束语

由m序列构造M序列反馈函数一直以来是实际应用中常见的构造方法，本文充分利用m序列构造M序列反馈函数的结构特性，结合函数变换以及函数派生，得到了一类个数较多且多项式表示和小项表示的重量都可以确定的M序列反馈函数。这种构造丰富了由m序列构造M序列反馈函数的方法，并且给出了其他项数和重量条件的反馈函数，克服了单一由m序列构造M序列反馈函数的构造缺陷，在实际应用中有更多可供选择的以多项式表示的M序列反馈函数。由于在构造过程中，多项式表示的方法还过于烦琐，是否还存在类似形式1的项数较少的M序列反馈函数的构造方法，是下一步研究的目标。

参考文献：

[1]中国科学院数学研究所代数组. 关于M序列反馈函数的构造方法[J].应用数学学报,1977,4:11-22.Institute of Mathematics,Chinese Academy of Sciences. The methods of constructingM-sequence feedback functions[J]. Acta Mathematicae Applicatae Sinica,1977,4:11-22.

[2]康庆德. GF(2)上M序列的构造方法[J]. 通信学报,1983(4): 2-10.KANG Q D. The methods of constructingM-sequence over GF(2)[J].Journal on Communications,1983(4): 2-10.

[3]熊荣华.M序列反馈函数的构造方法Ⅰ[J]. 应用数学学报,1986(2):227-236.XIONG R H. On methods of constructing the feedback functions ofMsequences I[J]. Acta Mathematicae Applicatae Sinica,1986(2): 227-236.

[4]朱士信.M序列反馈函数的派生方法[J]. 合肥工业大学学报(自然科学版),1991(4): 138-144.ZHU S X. Methods for the derivation of feedback functions ofMse-quences[J]. Journal of Hefei University of Technology,1991(4):138-144.

[5]章照止,罗乔林. 产生M序列的一个递推算法[J]. 系统科学与数学,1987(4): 335-343.ZHANG Z Z,LUO Q L. A recursive algorithm for the generation of De Bruijn sequences[J]. Journal of System Science and Mathematical Science Chinese Series,1987(4): 335-343.

[6]SAWADA J,WILLIAMS A,WONG D. A surprisingly simple de Bruijn sequence construction[J]. Discrete Mathematics,2016,339(1):127-131.

[7]ABBAS A. Stretching De Bruijn sequences[J]. Designs Codes &Cryptography,2017,85(2):381-394.

[8]高杨,刘松华,王中孝. 一种基于“编织法”的De Bruijn序列构造算法[J]. 电子学报,2018,46(1): 48-54.GAO Y,LIU S H,WANG Z X. A De Bruijn sequence construction algorithm based on “interleaving” construction method[J]. Acta Electronica Sinica,2018,46(1): 48-54.

[9]LI C,ZENG X,LI C,et al. Construction of De Bruijn sequences from LFSRs with reducible characteristic polynomials[J]. IEEE Transactions on Information Theory,2015,62(1):610-624.

[10]CHANG Z,EZERMAN M F,LING S,et al. Construction of De Bruijn sequences from product of two irreducible polynomials[J].Cryptography & Communications,2018,10(2):251-275.

[11]LI M,JIANG Y,LIN D. The adjacency graphs of some feedback shift registers[J]. Designs Codes & Cryptography,2016,82(3):1-19.

[12]LI M,LIN D. The adjacency graphs of LFSRs with primitive-like characteristic polynomials[J]. IEEE Transactions on Information Theory,2017,63(2):1325-1335.

[13]LI M,LIN D. De Bruijn sequences,adjacency graphs and cyclotomy[J].IEEE Transactions on Information Theory,2017,PP(99): 1.

[14]DONG J,PEI D. Construction for De Bruijn sequences with large stage[J]. Designs Codes & Cryptography,2016:1-16.

[15]万哲先,代宗铎,刘木兰,等. 非线性移位寄存器[M]. 北京:科学出版社,1978.WAN Z X,DAY Z D,LIU M L,et al. Non-linear shift register[M].Beijing: Science Press,1978.

[16]高鸿勋. 非奇函数是 M 序列反馈函数的一个充要条件[J]. 应用数学学报,1984(1): 9-10.GAO H X. A necessary and sufficient condition for nonsingular function to be feedback function of M-sequences[J]. Acta Mathematicae Applicatae Sinica,1984(1): 9-10.

[17]万哲先. 代数与编码[M]. 北京:科学出版社,1976.WAN Z X. Algebra and coding[M]. Beijing: Science Press,1976.

[18]高鸿勋. 求全部n级M序列及其反馈函数的一个方法与证明[J]. 应用数学学报,1979(4): 316-324.GAO H X. A method and proof of finding all n-stage of M-sequences and their feedback functions[J]. Acta Mathematicae Applicatae Sinica,1979(4): 316-324.

[19]许军进,尹克震. M序列反馈函数重量与项数的分析[J]. 杭州电子科技大学学报,2007(1): 24-28.XU J J,YI K Z. Analysis on weights and terms of feedback functions for Sequences[J]. Journal of Hangzhou Dianzi University,2007(1):24-28.