基于权重约束DEA和Tobit模型农业灌溉用水效率实证研究
----以黑龙江省为例
梁静溪,张安康,李彩凤
(1.哈尔滨理工大学经济管理学院,黑龙江 哈尔滨 150080;2.甘肃省兰州市兰州外语职业学院,甘肃 兰州 730101)
目前,我国农业用水资源匮乏,用水效率低下,农业灌溉用水效率的提高是构建节水型社会的基本要求和优先发展领域。黑龙江省是我国重要的商品粮基地,1998-2012年农业灌溉用水平均效率为0.913[1]。但近些年来,伴随着区域经济的发展,工业、生活与农业用水之间的竞争日益加剧,挤占农业用水现象与日俱增,农业用水供需失衡、灌溉效率低、地下水位持续下降等问题十分突出,因此,对此后2013-2015年农业灌溉用水效率的研究至关重要[2-4]。本文利用权重约束DEA和Tobit模型,基于2013-2015年黑龙江省13个地区的数据对农业灌溉用水效率进行测算和影响因素分析,并依据测算和分析结果提出节水灌溉的建议和措施。
1 概念界定与文献综述
农业技术效率是衡量经济资源有效利用程度的指标,主要分为两种情况,一种是投入要素数量不变情况下实际农业产出达到最大,另一种是产出要素数量不变情况下实际农业投入达到最小。农业灌溉用水(总)技术效率,即农业灌溉效率是指在一定生产技术和投入要素的情况下,最低灌溉用水量和实际灌溉用水量的比值,用公式可表示为:
(1)
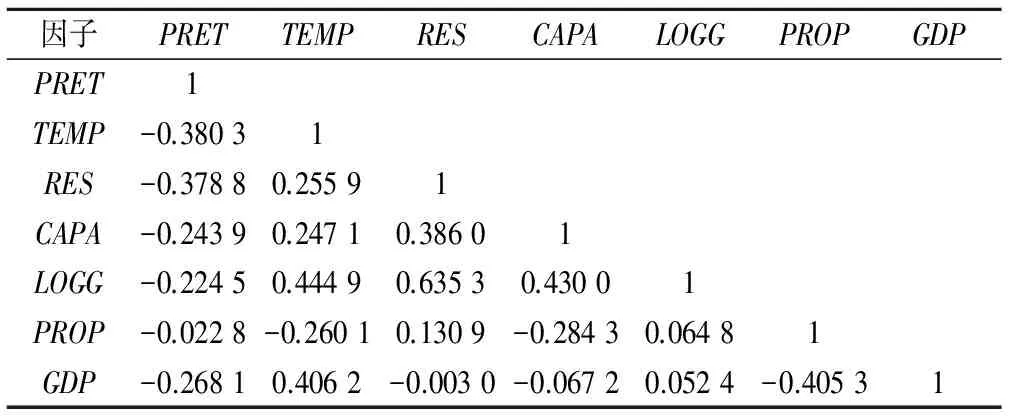
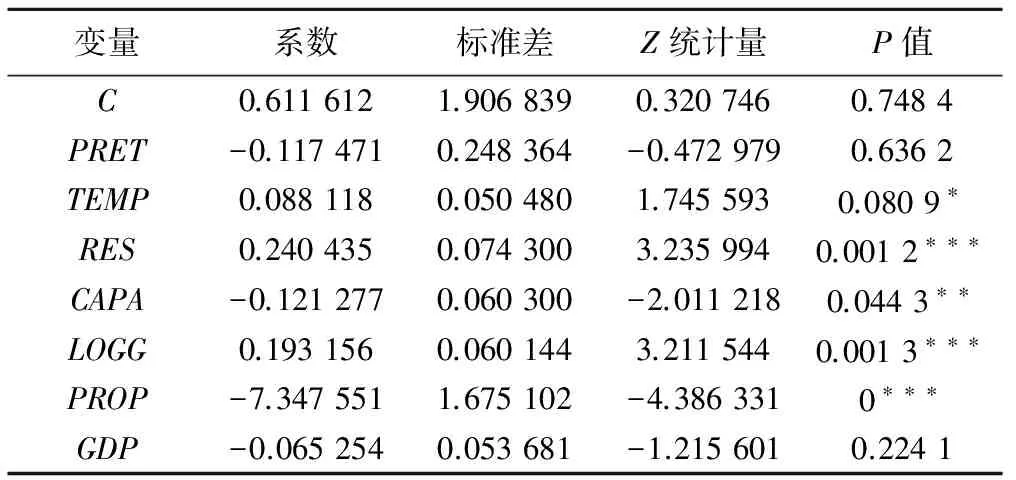
式中:WM代表最少灌溉用水输入量;WR代表实际用水输入量;WTE代表农业灌溉用水效率,WTE的范围是[0,1]。当WTE=1时,WM=WR,表明灌溉用水得到充分利用;当0 中外学者关于农业灌溉用水效率的研究很多,根据其研究方法不同,可归纳为以下3种: (1)运用随机前沿分析方法(SFA),Mcgockin et al.(1992年)、Omezzine、Zaibet(1998年)利用SFA方法分析了商业计划、天气预报等节水措施对灌溉用水效率的影响[5,6];Karagiannis et al.(2003年)利用超越对数的SFA方法对希腊克里特地区1998-1999年50个农场的灌溉用水效率进行测算与分析[7];Dhehibi et al.(2007年)利用SFA方法分析了突尼斯纳布尔地区的灌溉用水效率[8];耿献辉,张晓恒(2014年)运用SFA模型考察了新疆地区棉花灌溉用水效率[9]。综合上述学者的研究结论发现,SFA方法可以充分考虑随机误差影响,测算的技术效率精确度高。 (2)运用数据包络分析方法(DEA),Rodiguez et al.(2004年)利用数据包络方法测算了西班牙灌溉区的效率值[10];Lilienfeld和Asmild(2007年)运用DEA方法对美国堪萨斯州西部地区43个灌溉区的用水效率进行了分析与测算[11];Yilmaz et al.(2009年)运用DEA方法对土耳其的门德雷斯盆地灌溉区进行了测算[12];王学渊(2009)利用1997-2006年31个省份的面板数据,采用DEA方法对中国宏观层面的灌溉用水效率进行测算与分解[13];佟金萍,马剑锋(2015年)基于1998-2011年长江流域10个省份的面板数据,运用超效率DEA模型对流域内农业用水效率进行了测度[14];Watto和Mugera(2015年)运用DEA方法测算了巴基斯坦地区甘蔗种植的灌溉用水效率[15];杨扬,蒋书彬(2016年)基于1998-2012年面板数据,运用DEA方法对我国农业灌溉用水效率进行研究[1];Pereira和Marques(2017年)对前人关于农业灌溉用水效率的研究进行了总结,发现DEA方法是测算农业灌溉用水效率最常用的方法之一[16]。综合上述学者的研究结论表明,DEA方法不指定生产函数的形式,应用灵活,且在处理多产出模型较方便。 (3) 将SFA和DEA两种方法相结合,王学渊(2010年)利用DEA和SFA两种方法对中国省区的灌溉用水效率进行了比较,发现两种方法测算出来的效率值基本一致[17];孙天合(2013年)运用DEA和SFA两种方法对陕西关中地区农业用水技术效率和经济效率进行了测算,结果表明,基于DEA方法测算的是灌溉成本效率,而基于SFA方法测算的是农业用水配置效率[18]。综合上述学者的研究结果发现,DEA和SFA最终测算的效率差异较小,且DEA测算的是灌溉成本效率,SFA测算的是农业用水配置效率。 整理相关文献发现,现有的研究具有以下几点不足之处:①研究模型不够精准,模型中都是运用单纯的DEA或SFA方法,没有加入权重约束的条件,不能反映出决策者意愿的主观因素,缺乏全面性;②研究范围狭窄,已有文献都是研究全国、省际或灌溉区之间的用水效率问题,很少有人研究关于省际内城市之间灌溉用水效率之间的差异。因此,为了改进已有研究的不足,本文利用具有权重约束的DEA方法,对黑龙江省13个地区的灌溉用水效率进行测算,一方面降低了传统DEA模型出现的大范围高效率问题,另一方面避免了输入要素权重值为0的问题,能很好地反映决策者意愿,且利用Tobit模型,从自然气候、水利设施、农业用水和经济发展四个方面考虑,更能全面的分析黑龙江省各地区灌溉用水效率的影响因素。 数据包络模型(DEA)是一种分析决策单元相对效率的线性规划方法。虽然DEA模型有其自身的缺点,但测算灌溉用水效率是在确保农业产值下可节约的水资源量,属于分向量,利用随机前沿方法(SFA)实现较困难。当规模报酬可变时,测算得到纯技术效率(BCC)和规模效率;当规模报酬不变时,测算得到总技术效率(CCR)。与此同时,基于投入产出距离函数,DEA可分为投入型和产出型,投入型是为测算相同产出水平下最小投入要素的效率,产出型是为测算相同投入水平下最大产出差距。本文研究的是水资源匮乏之下可节约水量,因此选择投入型的DEA模型,且对规模报酬是否可变进行了测算与比较。 假设有n个决策单元,m个投入要素和s个产出要素,对于第p个决策单元,XP={X1p,X2p,X3p,…,Xmp}T为DMUi的投入要素,YP={Y1p,Y2p,Y3p,…,Ysp}T为DMUi的产出要素,则由Charnes等人提出投入导向的CCR模型如下: (2) st: uk、vj≥0k=1,2,…,sj=1,2,…,m 式中:yki表示DMUi对第k种输出的产出量;xji表示DMUi对第j种输入的投入量;uk表示对k种输出的度量;vj表示对j种输入的度量。上述分式方程式可以根据C2转换为如下线性规划问题。 Charnes_Coopers(C2)变换: st: (3) μk,wj≥0k=1,2,…,sj=1,2,…,m 公式(3)被计算n次,以确定所有DMU的相对效率得分。一般而言,如果DMU的得分为1,则认为DMU是有效的,小于1则意味着效率低下。 如果DMU是无效的,其他有效单元的组合可以在相同投入要素情况下生产更多的产出,或者使用较少投入要素生产一样的产出。这些有效单元可以从对偶过程中获得,如下所示: minθ st: (4) λ≥0i=1,2,…,n 式中:θ表示效率值;λi表示对偶变量。 由于我们只考虑水资源投入的灌溉用水效率,因此进一步构建分向量DEA模型[19],其模型如下: minθ st: (5) λi≥0i=1,2,…,n DEA中另一个经典模型为BCC模型,其主要不同在于模型λi和等于1。如图1所示,包络面可采用规模报酬不变的CRS形式和可变的VRS形式。 图1 CRS(CCR)和VRS(BCC)前沿面 如前所述,在确定DMU效率值时,DEA模型并没有对权重加以限制,这就允许决策单元可通过放弃不适当投入和产出权重来实现相对较高的效率,导致效率值与现实不符。因此,本文在传统DEA模型中加入权重约束来解决这个问题,参考国外相关文献[20,21],将权重约束条件形式设置如下: (6) 式子中:βi、αi以及ζr、θr分别代表决策者主观信息输入、输出的上下限,将约束条件加入到传统DEA模型即得到具有权重约束的DEA模型。此外,约束条件的个数为[22]: (7) 式中:I为输入变量的个数;O为输出变量的个数 Tobit模型是一种解决因变量是受限变量的模型,其中,受限因变量是指因变量的观测值被约束条件所限制,以至于不能反映实际状态,当出现这种状态时,一般采用最大似然法估计模型参数。由于DEA效率值的范围是[0,1],宜采用Tobit模型,其形式可表示为: 式中:i表示地区;t表示时间;WTEit表示效率值;μit表示待估参数;Zit表示影响农业灌溉用水的自变量;εit表示正态分布的误差项。 本文选用农作物灌溉面积、农业机械总动力、农业劳动投入、农业总产值和相应反映决策者意愿的权重作为衡量指标,此外,由于测算农业灌溉用水效率问题,所以采用农业灌溉用水量这一指标,如表1所示。与此同时,根据表2各投入产出变量之间的相关系数可看出,灌溉用水量与农业总产值的相关系数为0.444 8,反映了在农业生产中水资源至关重要。 表1 农业灌溉用水效率评价指标 表2 投入与产出要素之间的相关系数 本文数据均来自《中国统计年鉴》(2014-2016)、《黑龙江省统计年鉴》(2014-2016)、黑龙江省水资源公报(2013-2015)。其中,农业灌溉用水量在年鉴中没有直接找到,使用农业用水总量的90%代替[23],此外,指标数量m与决策单元数目n保持2m≤n≤3m[24]的关系,本文中m为5,n为13,满足10≤13≤15,从而保证指标体系的合理性,且论文中数据都是经过归一化处理,进一步保证数据的稳定性。 利用权重约束DEA模型对黑龙江省13个地区进行评价,请20位农业领域的专家分别对四个输入指标给出等级分数,得到矩阵V。 (9) 根据层次分析法计算权重约束DEA模型得到以下向量: μ=(1.21,1.22,2.83,1.13,2.6,2.4)′ σ=(0.31,0.34,0.89,0.36,0.8,0.76)′ μ-3σ=(0.2,0.2,0.15,0.06,0.2,0.11)′ μ+3σ=(2.05,2.25,5.51,2.21,5,4.69)′ α=(0.03,0.07,0.28,0.62)′ β=(0.44,0.3,0.2,0.06)′ 进而求出输入和输出指标间两两比较重要性比率的上下限,从而得到权重约束条件为(10)式,其中由(7)式得出有6个约束条件。 根据公式(5),基于2014年黑龙江省13个地区的数据,运用EMS软件对不加入权重约束的CCR和BCC模型进行测算,如表3所示,CCR和BCC模型测算的效率值普遍很高,且部分投入要素的权重为0,例如,灌溉面积的权重为0,说明灌溉面积对生产产值没有任何贡献,与现实不符;灌溉用水量的权重为0,是不合理的,因为水是灌溉农业的必要条件。因此,运用这种方法测算的结果与实际情况严重偏离。 表3 没有权重约束的CCR与BCC模型结果 注:左边是CCR模型结果,右边是BCC模型结果。 为了解决上述问题,本文在模型中加入权重约束来测算合理的效率和权重,根据公式(6)的约束条件,得到表4的权重[25],运用EMS软件得出关于CCR和BCC模型具有权重约束的结果,如表5所示,发现具有权重约束比没有权重约束的效率值普遍低,且投入要素的权重都不为0,与实际相符。哈尔滨、大庆、佳木斯、牡丹江、绥化的效率值高,表明这些地区充分利用农业灌溉用水,而鹤岗和大兴安岭地区的效率值低,表明这些地区灌溉用水效率存在改进空间。 表4 投入和产出要素的权重 根据总技术效率(CCR)和纯技术效率(BCC)得到规模效率,如表6,结果发现七台河地区DEA无效是由于规模效率无效导致的,表明该地区农业灌溉规模小,可通过扩大规模来提高用水效率;鹤岗地区DEA无效是由于纯技术效率和规模效率都无效导致,可通过扩大灌溉规模和改善技术来提高用水效率。综合来看,黑龙江省农业灌溉用水总技术效率为0.707 0,纯技术效率为0.816 3,规模效率为0.866 1。 本文进一步测算了2013和2015年具有权重约束的CCR模型,做成了柱形图,如图2所示,在所研究的3年中,哈尔滨和黑河地区效率值不断提高,齐齐哈尔、大庆、佳木斯和大兴安岭地区效率值先提高后降低,尽管如此,黑龙江省大部分地区3年的效率值无显著变化,表明测算结果的平稳性和可靠性。 采用DEA模型对黑龙江省13个地区的农业灌溉用水效率进行测算,效率值不尽相同,对此,利用Tobit模型分析各地区效率值的影响因素,找出农业用水差异的原因。 表5 具有权重约束的CCR和BCC模型结果 表6 总技术效率、纯技术效率和规模效率值 图2 2013-2015年黑龙江省13个地区总技术效率值 (1) 自然气候因素。降水量是评价地方水资源丰裕度的指标。黑龙江省年降水量平均在400~800 mm,但受水汽入流方向、地理位置和地形的影响,地区分布不均,存在山区大平原小、中部和南部大、西部和北部小的特点。一方面,一个地区降水量多,农业所需水量就少,用水效率高,两者呈正向关系;另一方面,降水量多的地区,农户灌溉方式相对传统,用水效率低,两者呈反向关系。气温高有利于农作物生长,使得用水效率提高,与此同时,气温高也增加水分蒸发,导致用水效率低下,因此,假设降水量和气温与农业灌溉用水效率都存在双向影响。 (2) 水利设施状况。农田水利设施在农业生产中至关重要,可以保证粮食和农业生产,强化农业在国民经济中的重要地位。基于数据可得性,选取水库数量、水库容量和除涝面积代表水利设施状况,水库数量越多,容量越大,说明可以存储和利用的水资源量多,利用效率就高。而且,除涝面积可以保证农作物的产量,也利于提高农业灌溉用水效率,因此,假设水库数量、水库容量和除涝面积与农业灌溉用水效率都存在正向影响。 (3) 农业用水特征。农作物可以划分为经济和粮食作物,黑龙江省的粮食和经济作物主要有小麦、玉米、棉花、大豆等,由于不同农作物用水情况不同,因此农作物种植结构会作用于用水特征,导致农业用水特征发生很大变化。本文选取粮食播种面积的比重来说明农业用水特点,粮食作物种植面积越大,农业用水效率就越低,因此,假设粮食作物播种面积占总播种面积的比重与农业灌溉用水效率存在反向影响。 (4) 经济发展程度。水资源作为一种稀缺性经济资源,由于不同的教育水平和经济发展程度,人们对用水效率的关注程度也不同,节水意识也就产生较大差异。本文用人均GDP来衡量经济发展状况,人均GDP越多,经济发展程度越高,人们的节水意识越强,因此,假设人均GDP与农业灌溉用水效率存在正向影响。 表7 Tobit模型变量及影响效应假设 本文将2013-2015年黑龙江省13个地区的农业灌溉用水总技术效率作为被解释变量,降水量、气温、水库数量、水库容量、除涝面积、粮食作物面积占总播种面积的比重和人均GDP作为解释变量,建立如下Tobit模型(11)[26]: WTEit=μit+μitPRETit+μitTEMPit+μitRESit+ μitCAPAit+μitLOGGit+μitPROPit+μitGDPit+εit (11) 式中:i表示地区(1~13);t表示时间(2013-2015年)。 本文采用Eviews8.0对上述所建立的Tobit模型进行回归,由于考虑到影响因素太多,可能存在多重共线性问题,因此计算各影响因素之间的相关系数(表8),结果表明,影响因素之间不存在多重共线性,运行模型得到结果(表9)。 表8 影响因素之间的相关系数 回归结果表明:降水量与农业灌溉效率成反比,表明黑龙江省各地区农户的灌溉方式比较传统,用水效率低,虽然存在这种可能性,但是这个结果不显著,说明降水量对黑龙江省农业灌溉用水效率影响小;气温与农业灌溉效率成正比,气温高利于农作物生长,且这种影响在10%水平下显著。 表9 Tobit模型结果 注:*,**,***分别表示在10%,5%和1%水平下显著其中,原始数据经过了对数化处理,左边截断为无穷,右边为1。 水库数量、除涝面积与农业灌溉用水效率成正比,水库数量越多可以利用的水资源越多,用水效率越高,同理,除涝面积也可以保证农作物产量,提高农业灌溉用水效率,且这两种因素都是显著的,然而,与预期假设不一样的是水库容量,水库容量与农业灌溉用水效率成反比,可能是由于水库容量多,水量充足,人们节约用水的概念缺少,浪费水资源,使得农业灌溉用水效率低下。 粮食作物面积占总播种面积的比重与农业灌溉用水效率成反比,尽管经济作物的用水量要比粮食作物多,但其价值远远大于粮食作物,因此经济作物单位产值要比粮食作物大,粮食作物种植面积越大,用水效率越低,且这种影响是显著的。 人均GDP与农业灌溉用水效率成反比,人均GDP越高,经济发展程度越高,农业用水效率也越高,但是结果与我们假设相反,可能是由于虽然经济发展程度高,但农田水利设施是公共物品,农民不会在水利设施上花费资金,灌溉用水效率也不会发生变化,且这种影响也不显著。 本文基于2013-2015年黑龙江省13个地区的投入产出数据,采用具有权重约束的DEA模型重点分析了2014年灌溉用水技术效率、规模效率和纯技术效率,并对3年的灌溉用水技术效率进行比较,最后运用Tobit模型分析了农业灌溉用水技术效率的影响因素。主要研究结论有: (1) 基于2014年黑龙江省13个地区的投入产出数据,运用具有权重约束的DEA模型测算的灌溉用水技术效率更加符合黑龙江省实际情况,一方面排除了大部分地区效率值都是1的情况,另一方面排除了大部分投入要素权重为0的情况;在此基础上,进一步测算了规模效率和纯技术效率,发现技术效率等于两者乘积,且各自均值为0.707 0、0.816 3、0.866 1;最后,整体分析了2013-2015年的灌溉用水技术效率,通过柱状图可以看出,各地区效率值变化不一,但总体上无显著差异,比较稳定。 (2) 从Tobit模型的结果可知,降水量、水库容量、粮食作物播种面积占总播种面积的比重和人均GDP与农业灌溉用水效率呈负向效应,气温、水库数量和除涝面积与农业灌溉用水效率呈正向效应,且除了降水量和人均GDP不显著,其他影响因素都是显著的,因此,可通过增加水库数量和除涝面积,适当减少水库容量和粮食作物的种植面积,来提高黑龙江省各地区农业灌溉用水技术效率。 为了提高灌溉用水效率,缓解黑龙江省各地区水资源短缺的状况,综合上述研究结论,提出以下建议启示: (1) 引入水价来促使农户节约用水。限制于传统用水习惯和意识,农民对水资源价格反应不明显。从本文的研究结论也可以看出人均GDP和水库容量都与灌溉效率成反比,主要是由于农户节水意识弱,认为农田水利设施属于公共物品,不需要进行节约用水,造成水资源浪费,灌溉用水效率低下。因此,我们要对水价进行合理的规定,对水资源的经济属性进行合理的宣传,使得农户意识到水也是一种商品,使用时需要支付费用,自觉产生节水意识,提高农业灌溉用水效率。 (2) 引入制度来规范水资源管理。通过引入制度要素来成立农民用水协会等相关组织,农民用水协会是一种管理模式,这种模式主要解决农民节水意识不强问题。成立相关组织,能够很好增强农民自我约束能力,使得基础设施维护情况得到改善,充分发挥农民自治组织在提高灌溉用水效率中的重要作用。 (3) 引入技术来实现节水灌溉。灌溉技术不同对农业灌溉用水效率有很大影响,且差异明显。在技术上,一方面可以适当改变农作物种植的结构,研究结果表明粮食作物播种面积比重与效率成反比,因此可以构筑与用水量相适应的生产布局,适当降低粮食作物播种面积,扩大节水作物播种面积;另一方面可以推广简单易学的节水灌溉技术,改变传统的灌溉方式,研究结果表明气温、水库数量和除涝面积对效率的影响都是正向且显著的,因此,可以扩大常用地膜等材料的覆盖面积,促进作物的蒸腾作用,提高农业灌溉用水效率。 参考文献: [1] 杨 扬, 蒋书彬. 基于DEA和Malmquist指数的我国农业灌溉用水效率评价 [J]. 生态经济,2016,(05):147-151. [2] 付 强, 刘 巍, 董淑华, 等. 黑龙江省灌溉水利用效率影响因素分析 [J]. 应用基础与工程科学学报,2017,(02):286-295. [3] 付 强, 刘 巍, 刘 东, 等. 黑龙江省灌溉用水效率指标体系空间格局研究 [J]. 农业机械学报,2015,(12):127-132. [4] 龚时宏, 吴文勇, 廖人宽. 东北粮食主产区高效节水灌溉技术与集成应用 [J]. 中国环境管理,2017,(01):111-112. [5] Mcgockin J T, Gollehon N, Chosh S. Water conservation in Irrigated agriculture: a stochastic production frontier m-odel [J].Water Resources Research,1992,28(1):305-312. [6] Omezzine a, Zaibet I. Management of modern irrigation systems in Oman: allocativevs irrigation efficiency[J]. Agricultural Water Management,1998,37(1):99-107. [7] Karagiannis G, Tzouvelekas V, Xepapadeas A. Measuring irrigation water efficiency with a stochastic productio-n frontier [J]. Environmentaland Resource Economics,2003,26(1):52-72. [8] Dhehibi B, Lachaal L., Elloumi M, et al. Measuring irrigation water use efficiency using stochastic production f-rontir: an application on citrus producing farmsin tunisia [J]. African Journal of Agriculturaland Resource Economics,2007,1(2):1-15. [9] 耿献辉, 张晓恒, 宋玉兰. 农业灌溉用水效率及其影响因素实证分析----基于随机前沿生产函数和新疆棉农调研数据 [J]. 自然资源学报,2014,(06):934-943. [10] Rodiguez JA, Camacho PE, LOPEZ LR. Application of Data Envelopment Analysis to Studies of Irrigation Efficiency in Andlusia [J]. Journal of Irrigation and Drainage Engineering,2004,130(3):175-183. [11] Lilienfeld A, Asmild M. Estimation of excess water use in irrigated agriculture :A Data Envelopment Analysis approach [J].Agricultural water management,2007,94:73-82. [12] Yilmaz B, Yurdusev MA, Harmancioglu NB. The assessment of irrigation efficiency in buyuk menderes basin[J]. Water Resources Management,2009,23(6):1081-1095. [13] 王学渊. 基于数据包络分析方法的灌溉用水效率测算与分解 [J]. 农业技术经济,2009,(6):40-49. [14] 佟金萍,马剑锋,王圣, 等. 长江流域农业用水效率研究:基于超效率DEA和Tobit模型 [J]. 长江流域资源与环境,2015,(04):603-608. [15] Watto MA, Mugera AW. Efficiency of irrigation water application in sugarcane cultivation in Pakistan [J]. Journal of the Science of Food and Agriculture,2015,(95):1860-1867. [16] Helga Pereira, Rui Cunha Marques. An analytical review of irrigation efficiency measured using deterministic and stochastic models [J]. Agricultural Water Management,2017:184. [17] 王学渊. 基于DEA和SFA方法的中国省区灌溉用水效率比较研究 [J]. 统计与决策,2010,(8):44-47. [18] 孙天合. 陕西关中不同灌区农业灌溉用水效率评价及其影响因素分析[D]. 陕西杨凌:西北农林科技大学,2013. [19] Fare R, Grosskopf S, Lovell C A K. Production Frontiers.Cambridge:Cambridge University Press, 1994:310-324. [20] Thompson RG, Langemeier, Ln Lee CT. The role of multiplier bounds in efficiency analysis with application to kansas farming[J]. Journal of Econometrics,1990,(46):93-108. [21] Wong YHB, Beasley JE. Restricting weight flexibility in data envelopment analysis[J]. Journal of the operational research society,1990,(41):829-835. [22] Joseph Sarkis. A comparative analysis of DEA as a discrete alternative multiple criteria decision tool[J]. European Journal of Operational Research,1998:543-557. [23] 翟浩辉. 因地制宜, 注重实效, 坚持不懈开展农田水利基本建设[EB/OL]. 中国水利网, 2002-09-06. [24] 叶世绮, 颜彩萍, 莫剑芳. 确定DEA指标体系的B-D方法 [J]. 暨南大学学报(自然科学与医学版),2004,(3):249-255. [25] R Allen, A Athanassopoulos, R G Dyson et al. Weights restrictions and value judgements in Data Envelopment Analysis: Evol-ution,development and future directions [J]. Annals of Operations Research.1997:13-34. [26] 唐建军. 陕西省灌溉用水技术效率及其影响因素研究[D]. 陕西杨凌:西北农林科技大学,2010.2 权重约束的DEA与Tobit模型构建
2.1 权重约束的DEA模型
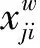
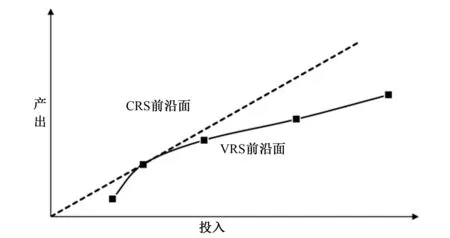
2.2 Tobit模型
3 变量设定与数据说明

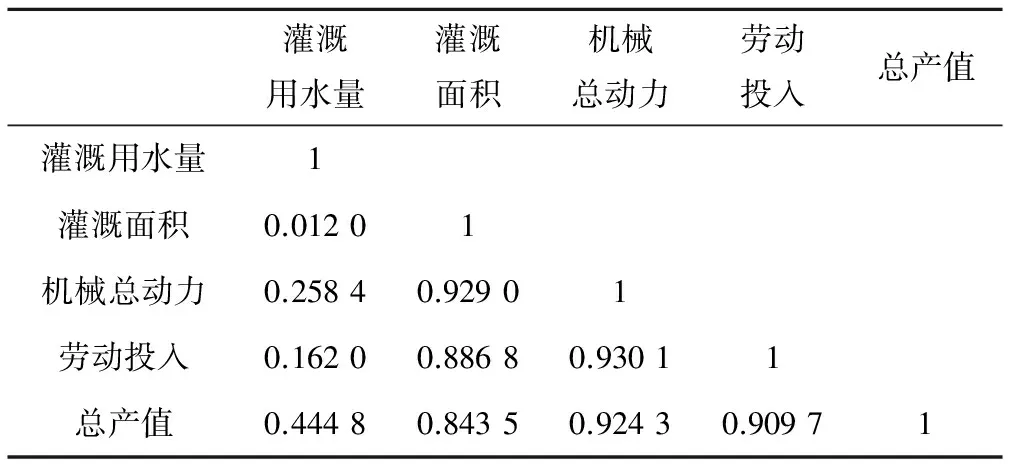
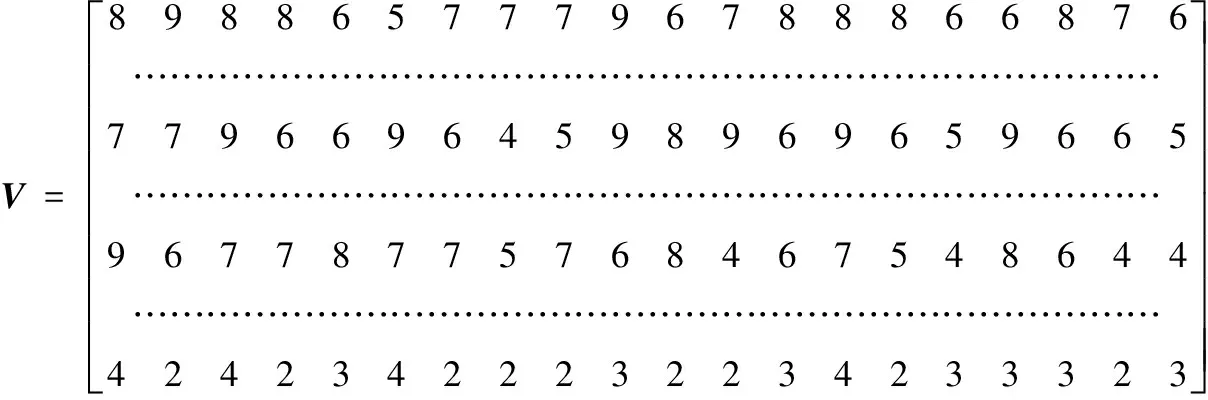
4 实证结果分析
4.1 农业灌溉用水效率测算

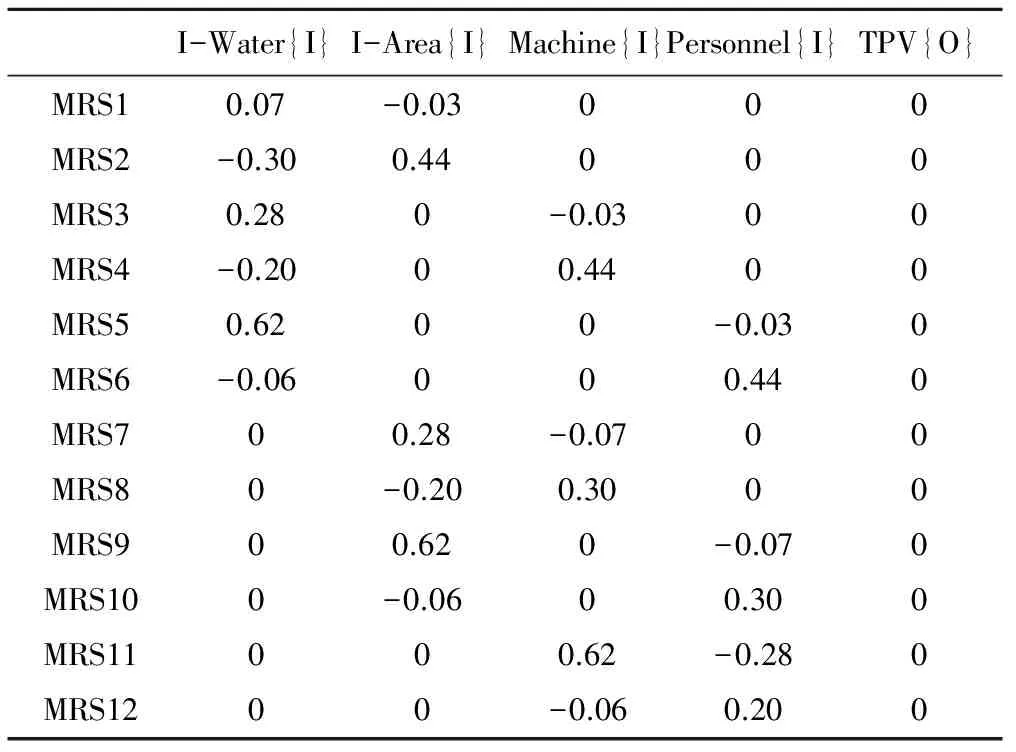
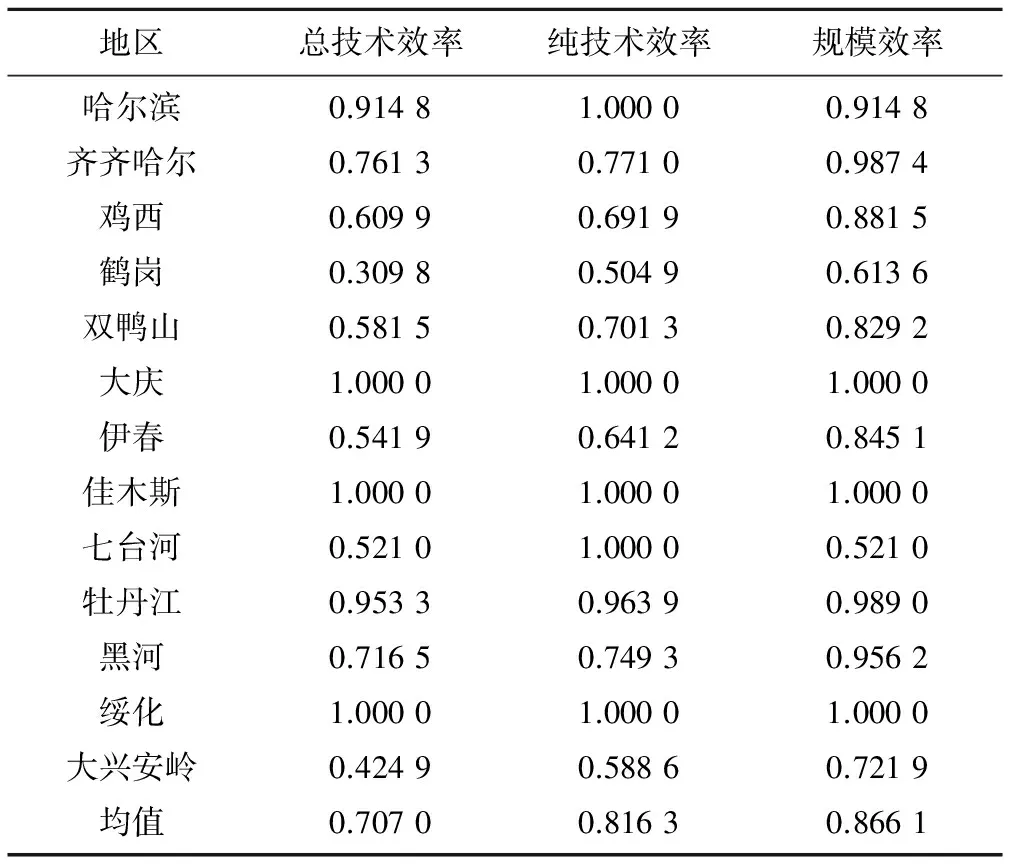
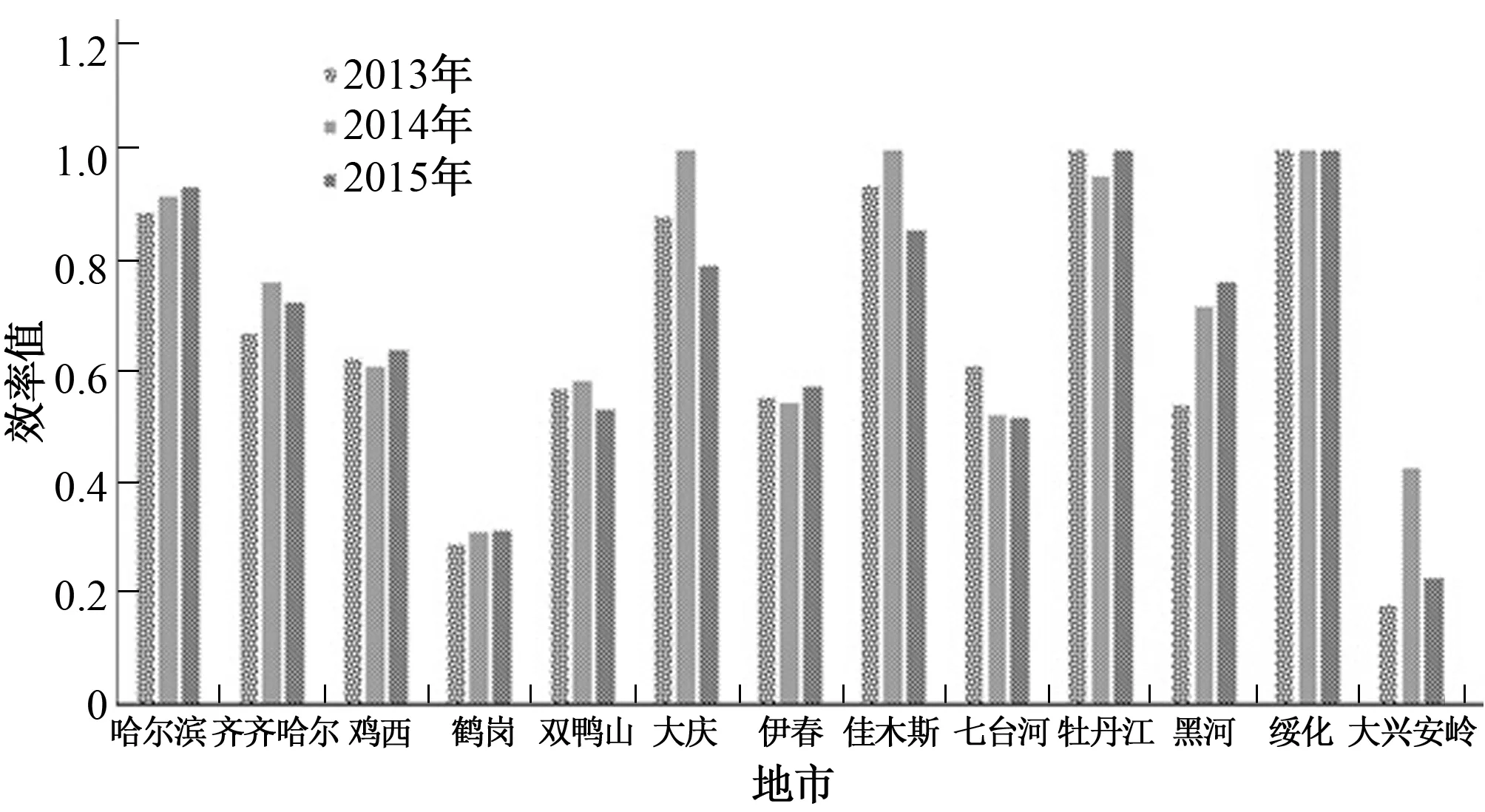
4.2 农业灌溉用水效率影响因素分析

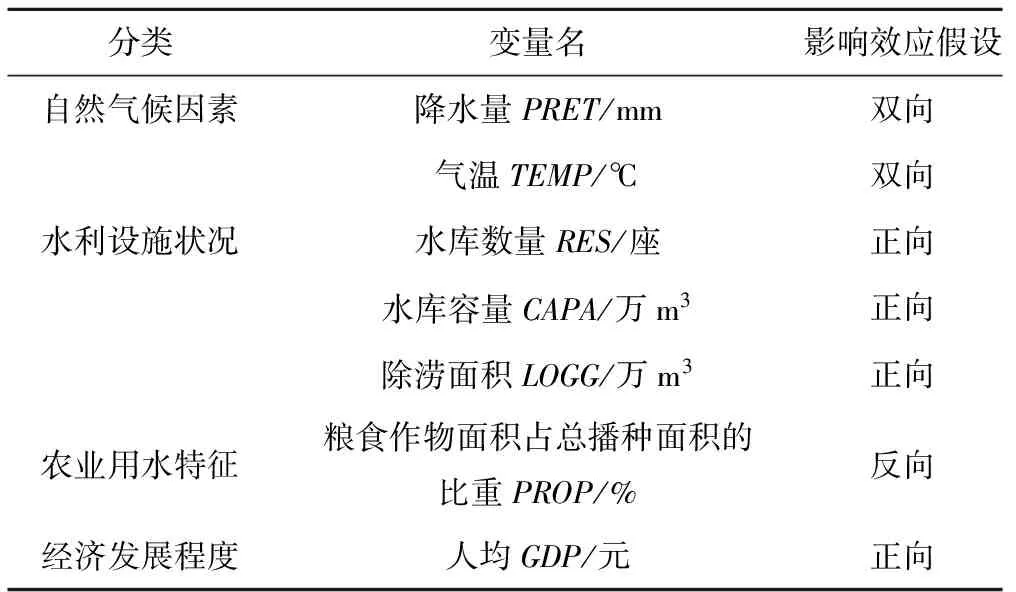
5 研究结论与建议启示
5.1 研究结论
5.2 建议启示

