高速电梯提升系统纵向振动建模与动态特性研究
吴虎城
(江苏建筑职业技术学院机电工程学院,江苏 徐州221116)
0 引言
曳引式高速电梯广泛应用于高层民用住宅、商办场所,其提升系统如图1所示,主要由曳引机、曳引绳、桥厢桥架、导向轮、对重、补偿绳以及张紧装置等组成。在这个由多部分组成的复杂系统中,曳引钢丝绳、导轨导向以及电气控制系统等设计制造、安装调试以及运行过程中的各种因素都有可能造成电梯曳引系统的振动。相对于普通电梯,高速电梯曳引系统的动态特性对载重、速度、高度等运行参数的变化而引起的激励更加敏感,尤其曳引系统的前几阶固有频率接近曳引机频率,从而导致纵向振动的加剧。所以研究曳引系统的动态特性对电梯提升性能的改善有着重要的意义。
1 提升系统建模方法相关研究
目前国内外专家学者对钢丝绳提升系统的建模方法主要有两种:集中参数的离散模型与分布参数的连续模型[1-2]。当研究重点是电梯提升系统的纵向振动时候,适合采用集中参数的离散模型。此时建模过程忽略曳引钢丝绳的柔性特征,将其认为是个变参数的弹簧-阻尼器,这样整个提升系统可看作一个多刚体振动系统。早期专家学者的研究对象主要是普通电梯系统,系统建模一般不涉及张紧装置[3-4]。而高速电梯通过采用张紧装置来平衡电梯对重与桥厢两侧的质量差值并保证电梯运行的稳定性。王艳军等[5]在考虑到张紧装置作用的同时,分析了高速电梯的振动频率,但是建模过程忽略了曳引钢丝绳和补偿钢丝绳的质量对提升系统动态特性的影响。吴慧等[6]建立了绕绳比1∶1的15自由度电梯提升力学模型,重点研究了高速电梯在不同速度、不同载荷条件下的固有频率,为进一步的动力学研究提供了基础。郭丽峰[7]等学者建立了12自由度的桥厢-导轨耦合系统水平方向振动模型,研究其动态特性。尹纪财[8]建立了垂直方向12自由度的动力学模型并进行仿真,通过正交实验的方法获得曳引钢丝绳、绳头弹簧及减振垫对电梯提升系统振动的影响。如图1所示。

图1 高速电梯提升系统示意图
上述研究或是对某一低速电梯进行动态响应分析,或是忽略曳引钢丝绳的本身质量属性,或是没有将张紧装置考虑进去,本文将综合考虑曳引钢丝绳、补偿钢丝绳的质量以及张紧装置的影响进行电梯提升系统的纵向振动建模,并采用离散化提升行程的方式来获得高速电梯运行过程的动态响应。
2 提升系统动力学模型建立
高速电梯相对于普通电梯的行程较长,曳引钢丝绳和补偿钢丝绳的质量一般达到几百千克甚至上千千克,所以在提升系统的动力学建模过程中钢丝绳的质量不再可以忽略。钢丝绳的离散数量越多,则计算结果越精确,但是计算工作量也越复杂。参照文献[6],本文将相关钢丝绳分为4段,建立曳引比为1∶1的电梯提升系统15自由度的纵向振动动力学模型如图2所示。图中,各个参数的物理意义说明如下:m1~m5分别为曳引轮、对重、桥架、桥厢、张紧装置的等效质量;k0、kt、kp分别为曳引机底座等效刚度、曳引机的抗扭刚度、张紧装置的等效刚度;c0、ct、cp分别为曳引机底座、曳引机、张紧装置的阻尼;φ1、φ5分为m1、m5的角位移;mr1~mr4分别为曳引侧各分段钢丝绳的等效质量;mc1~mc4分别为补偿侧各分段钢丝绳的等效质量;kr1~kr4、k*r1~k*r2分别为曳引侧各分段钢丝绳的等效刚度;cr1~cr4、c*r1~c*r2分别为曳引侧各分段钢丝绳的阻尼;kc1~kc4、k*c1~k*c2分别为补偿侧各分段钢丝绳的等效刚度;cc1~cc4、c*c1~c*c2分别为补偿侧各分段钢丝绳的等效阻尼。
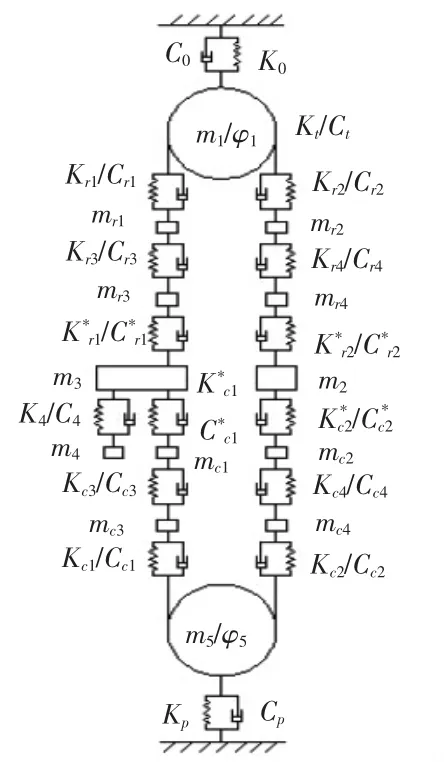
图2 高速电梯提升系统动力学模型
以纵向向上为线位移正方向,逆时针方向为角位移正向,对图2的电梯提升系统动力学模型应用拉格朗日方程,整理得到15自由度的振动微分方程:
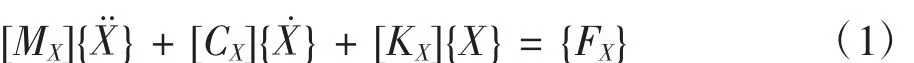
式中,[MX]、[CX]、[KX]分别为提升系统的质量矩阵、阻尼矩阵和刚度矩阵;X¨、X˙、X、FX分别为系统的加速度、速度、位移和激励向量。其中,X = {x1,x2,x3,x4,x5,xr1,xr2,xc1,xc2,φ1,φ5,xr3,xr4,xc3,xc4};FX={Fx1,Fx2,Fx3,Fx4,Fx5,0,0,0,0,0,0,0,0,0,0},Fx1、Fx2、Fx3、Fx4、Fx5分别为曳引轮、对重、桥厢架、桥厢以及张紧装置所受的外力,各分段钢丝绳的受力忽略不计。
对多自由度系统进行模态分析时候,可不设置外载荷边界条件,而系统阻尼较小忽略不计,所以上述振动微分方程相应转变为:

3 提升系统固有频率计算
3.1 电梯运动状态模拟
选取某型号高速电梯为例,该高速电梯额定载荷1 600 kg,桥厢架自重1 700 kg,由8根直径为13 mm的钢丝绳提升,每根钢丝绳的线密度为0.575 kg/m.为了更好模拟高速电梯在整个提升运动过程中的运动状态,采用梯形加速度加减速运行方式,将其提升过程分为七个阶段,即加速度由零增至最大、保持不变、减至零值、匀速、加速度减至最大、保持不变、增至零值。通过定义每个阶段的时长,设定提升过程最大加速度为1 m/s2,最大速度为6 m/s,最大提升距离为168 m,利用matlab软件即可获得电梯提升上行过程的运行状态曲线如图3所示。

图3 电梯提升系统运行状态曲线
3.2 固有频率计算
电梯提升系统运行过程中,提升距离的变化必然引起曳引机两侧、张紧装置两侧的钢丝绳长度的变化,此时动力学模型中的质量矩阵、刚度矩阵也随之变化,所以上述振动方程(2)属于变系数微分方程,求解过程相对复杂,如将电梯提升行程离散化,即将整个提升距离分为任意多个提升位移间段,则每个提升位移间断点的曳引钢丝绳、张紧钢丝绳长度可以确定,那么相应的振动方程也变成常系数微分方程。电梯实际运行过程中的起始点(桥厢位移为0 m)、中间点(桥厢位移为84 m)、终点(桥厢位移为168 m)三个位置具有代表性,则研究提升系统的动态特性也主要针对这三个提升位置,同时每个位置分为空载、半载、满载三种工况,表1即为计算获得的电梯提升系统在三个位置不同载荷工况下的前6阶固有频率。

表1 电梯提升系统固有频率(Hz)
从表1可以看出,三种工况下,第一阶固有频率随着提升位移的增加而略有增加;各阶固有频率一般随负载的增加而降低,阶数越高,负载对固有频率的影响不再明显;电梯提升系统的第一阶固有频率约为3 Hz,比较接近曳引机的转动频率,有发生共振的可能,这与电梯实际运行时振动感较为强烈相符合。
将上述计算结果与文献[1]进行对比,可以发现初阶固有频率比较接近,说明该计算方法较为可靠。采用该方法建立的纵向振动方程属于常系数微分方程,求解过程相对简单。
4 结论
(1)针对高速电梯提升系统的结构复杂性,构建曳引比为1∶1的15自由度提升系统动力学模型,应用拉格朗日方程建立相应的振动微分方程。
(2)采取提升行程离散化的方法,将变系数微分方程转变成常系数微分方程,求解获得电梯空载、中载以及满载三种工况在提升起始点、中间点、终点位置情况下的固有频率。
(3)计算结果表明,三种工况下,第一阶固有频率随着提升位移的增加而略有增加;各阶固有频率一般随负载的增加而降低,阶数越高,负载对固有频率的影响不再明显;电梯提升系统的第一阶固有频率与曳引机的转动频率接近,在电梯实际运行时,有发生共振的可能,设计电梯提升系统时候要注意避免。
参考文献:
[1]包继虎.高速电梯提升系统动力学建模及振动控制方法研究[D].上海:上海交通大学,2014.
[2]李 菁,李济顺,刘 义,等.虚拟样机技术在摩擦式提升机动力学分析中应用[J].机械设计与制造,2014(9):238-241.
[3]张长友,朱昌明.电梯系统动态固有频率计算方法及减振策略[J].系统仿真学报,2007,19(16):3856-3859.
[4]武丽梅,巩煜琰,李雪枫.曳引式电梯机械系统垂直振动动态特性分析[J].机械设计与制造,2007(10):16-18.
[5]王艳军,任立刚,于 杰.电梯系统动态固有频率分析[J].机械,2010,37(1):35-37.
[6]吴 慧,叶文华,沈 言,等.高速电梯垂直振动建模与实验分析[J].机械制造,2013,51(584):19-22.
[7]郭丽峰,张国雄,李醒飞,等.电梯桥厢—导轨耦合动力系统建模及其动态特性[J].机械工程学报,2007,43(8):186-190.
[8]尹纪财.中高速电梯曳引系统振动问题的研究[D].苏州:苏州大学,2011.

