基于分布估计-逐次逼近的弃水电量最小模型

刘 易，王丽萍，唐 勇，纪昌明，赵亚威

(1.华北电力大学 可再生能源学院，北京 102206；2. 国家电网公司国家电力调度控制中心，北京 100031)

随着社会经济的发展和电力系统中水电地位越发重要，水电的弃水电量也成为电力电量平衡计算中需要考虑的重要因素。吴东平等分析了弃水电量的成因，认为弃水电量是水电未达到理论发电量而损失的电量[1]。不合理的检修计划和备用配置会导致水电工作容量不足，水电因此产生弃水电量；不合理的出力分配也会导致火电因自身调峰能力不足，被迫增大出力，挤占水电工作位置，使水电产生弃水电量。刘方等通过建立梯级水电站上游调峰电站和下游反调节水库的协调调度模型，增强系统调峰能力，从水电站群的内部相互调度减小弃水电量[2]。乔娟等提出了小水电增效扩容补充方案评价，以减小小水电弃水电量[3]。张今通过定价方法吸纳弃水电量，通过经济手段，减少弃水电量带来的经济损失[4]。而弃水电量的产生，也和电力系统中的火电有着密切联系，减少弃水电量，需要从电网系统角度进行全面考虑。弃水电量是对能源的一种浪费，而建立弃水电量最小模型，通过对电力系统的电力电量平衡进行研究，从负荷、检修、备用配置方面，优化电力系统弃水电量，具有十分重要的意义。

对弃水电量最小模型的求解，得到最优的负荷分配方案，需要一个更全面系统考虑到检修、备用、出力的电力电量平衡算法。电力电量平衡是对电能进行跨区域、跨季节的统筹调配，实现全网内发电资源在一定周期内总体优化利用[5]。国内外对电力电量平衡的研究，主要针对电力电量平衡计算的各个部分而言的。在负荷分配方面，常用方法包括逐次切负荷法、余荷逐次后移法、剩余容量日利用小时控制法等[6-8]。在电源检修计划制定方面，传统采用等备用模型或等风险度模型[9]，现今多采用智能算法对检修计划进行优化，包括改进遗传算法、粒子群算法等[10,11]。在备用负荷分配方面也有将激励成本和期望停电损失引入计算模型[12]；或将峰谷电价和补偿机制引入到备用容量的确定中[13]。综上所述，对电力电量平衡计算的优化主要集中在过程中的某一部分，对完整考虑电力系统各电源负荷、备用、检修研究较少，其原因是电力电量平衡的约束条件较多，同时优化时，约束条件之间的联系较为复杂，研究难度较大。

从规划设计的角度上来说，电力电量平衡优化计算中重要的等式约束包括电力平衡、电量平衡、备用等式约束和检修等式约束。由于备用和检修等式约束时间维度不同，在优化计算时，难以同时满足。备用等式约束要求在各个时段内，系统内各个电源的备用容量之和等于系统所需的备用容量。检修等式约束则要求全时段各个电源的检修容量之和等于各个电源的装机容量。本文在分布估计算法(EDA)的基础上嵌入逐次逼近算法(SA)，实现2种算法的耦合，以此对各电站备用配置、检修计划进行优化；将各电站除去备用、检修后的剩余容量作为参与发电的最大工作容量，采用余荷逐次后移法进行出力分配；通过反复迭代计算，得出以弃水电量最小为目标的电力电量平衡优化计算结果。

1 弃水电量最小数学模型

弃水电量是指在弃水期内水电站实际发电出力未达到设计值而造成的电量损失[14]。造成水电弃水调峰的原因较多，涉及的问题也比较复杂，但主要是受电网负荷结构、电网客观条件、水库调节能力、火电综合调峰能力、经济政策等因素的影响。在电力系统负荷水平和电源结构稳定的情况下，导致水电产生弃水电量的主要有两个因素：一是水电站出力受阻，包括电网安全对发电出力的约束、电网消纳能力限制、检修备用分配不合理等，水电发电量无法达到预计发电量或无法完全被电网消纳。在电力电量平衡方面主要表现在，不合理的检修计划和备用负荷分配使水电站工作容量小于其月理论出力。二是调峰弃水，主要产生于汛期。汛期水电站的检修和备用将影响自身和火电的调峰能力，考虑到水电理论出力大，调峰能力差，运行位置通常在基荷或接近基荷的腰荷位置，系统调峰任务主要由火电承担。但由于火电机组存在出力爬坡限制，其调峰容量存在上限，故某些时刻为了满足火电调峰容量限制，火电将被迫抬高基荷出力，挤占水电工作位置，水电弃水调峰，无法达到理论发电量，产生弃水电量。

1.1 目标函数

根据弃水电量产生的原因，电力系统的弃水电量可以认为是系统内所有水电理论发电量和实际发电量之差，其中包括出力受阻弃水电量和调峰弃水电量。

弃水电量最小模型的目标函数如下：

(1)

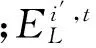
水电的实际发电量通过电力电量平衡计算，满足所有约束条件后，水电在负荷图中实际承担的电量。水电站理论发电量则是通过水电站上下游水位差、机组出力系数、发电流量和发电时间求得水电厂理论发电量[15]，计算公式如下：

(2)

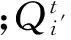
在电网规划设计阶段，水电理论发电量一般通过水电月平均出力求得，其通过水电典型水平年各月发电数据统计分析得到，代表了水电站在水平年各月的发电能力。除此之外，电网中的电力损耗与负荷相比较小，电量损耗也相比较小，所以在建立模型时，不考虑电力、电量损耗。

1.2 约束条件

电力平衡约束：

(3)

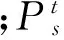
电量平衡约束：

(4)

式中：ESystem为各个计算时段内系统电量；Ei为i电站在计算时段内的发电量。

一般以年为周期的电力电量平衡计算需同时满足12个月典型日电力电量平衡约束。

系统备用等式约束：

(5)

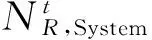
系统检修等式约束：

(6)

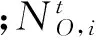
电源备用容量约束：

(7)

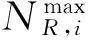
电源检修容量约束(检修资源约束)：

(8)

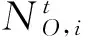
同时检修约束：

τb=τa

(9)

式中：τa为机组a检修开始时间；τb为与之相关的机组b检修开始时间。

电源检修互斥约束：

τb>τa+Ta

(10)

式中：Ta为机组a检修时间。

电源工作容量(出力)约束：

(11)

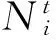
火电调峰容量约束：

maxPT-minPT≤maxPTη

(12)

式中：maxPT为一个典型日时段内火电出力的最大值；minPT为一个典型日时段内火电出力的最小值；η为火电的调峰系数，代表了系统内火电的调峰能力。

系统负荷分配时，一般优先计算水电，然后计算火电。若火电无法满足调峰约束，只能抬高火电基荷出力，放弃部分水电电量，以求达到系统的电力电量平衡。

2 分布估计-逐次逼近耦合算法(EDA-SA)

在电力电量平衡模型中，系统内所有电站各个时段的备用配置和全时段的检修计划都会对目标函数最终计算结果产生影响，即通过影响各电站的最大工作容量，来影响系统负荷分配。与此同时，平衡计算中需要满足的等式约束较多，各个约束条件之间存在相互联系，传统计算方法难以在满足约束条件的同时，找到优化方向。若用常规单一智能算法对该模型进行计算，则必须对种群个体进行频繁修正来满足约束条件，如此必然会影响最终的优化结果。故本文提出了分布估计-逐次逼近耦合算法，并结合余荷逐次后移法，对弃水电量最小模型进行求解，完成电力电量平衡优化计算。

2.1 分布估计算法

分布估计算法(EDA)是一种通过概率模型描述种群中精英个体在空间的分布的智能算法。该算法采用统计学习手段，从群体宏观的角度建立一个描述解分布的概率模型，然后对概率模型随机采样产生新的种群[16]。分布估计算法快速收敛的特性能有效提高算法计算效率，其算法特性使其在制定电站检修计划上表现优越。首先对每个电站的所有机组随机生成检修时间，满足全时段的检修等式约束；然后计算种群个体适应度，通过统计种群中精英个体的检修计划，分析各个电站在整个计算时段上检修容量的概率分布，以精英集作为种群进化的方向；最后按精英集检修容量的概率分布，在考虑检修约束的情况下，生成下一代种群各电站的检修计划。由于算法是通过逐台机组随机生成检修时间，所以可以根据具体检修条件，影响检修计划的生成。

2.2 逐次逼近算法

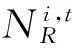
(1)按电站承担备用上限大小，从小到大排序，在各个电站承担备用的上下限范围内随机生成初始轨迹，如下式，并根据备用等式约束对初始轨迹进行修正，使其满足等式约束。

(13)

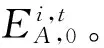
(14)

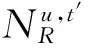
(3)所有月份的备用优化完成后，得到在固定检修下，备用最优的年弃水电量。基于逐次逼近算法的备用优化流程图如图1所示。

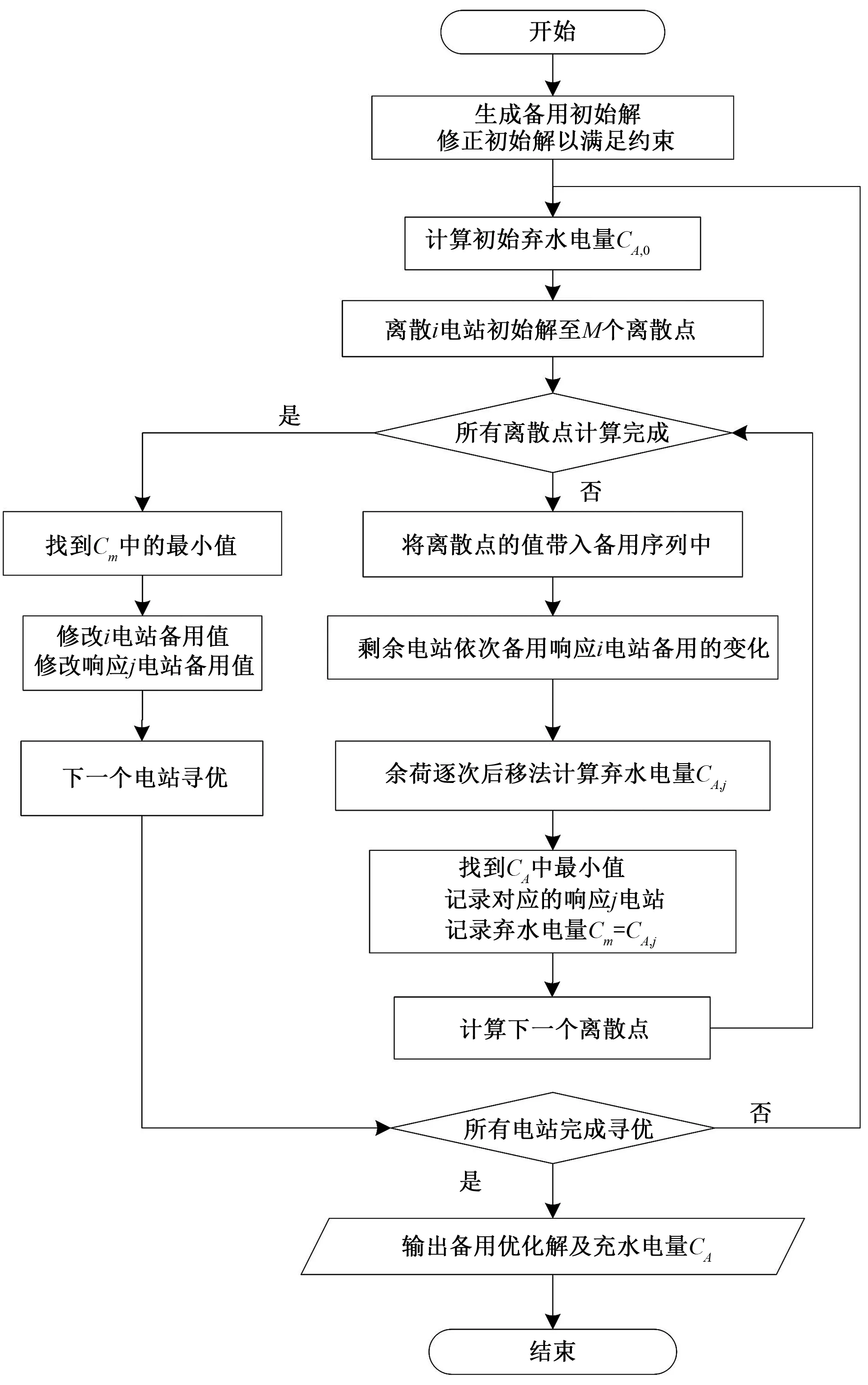
图1 基于逐次逼近算法的备用优化计算流程图Fig.1 Flow chart of optimization for reserve based on successive approximation algorithm

在备用优化之中，弃水电量的计算则是采用余荷逐次后移法。余荷逐次后移法是通过水电站最大工作容量的约束，尽可能利用系统可调日电量，达到水电站群被系统吸收日电量最大的目的，在系统最大负荷处充分利用各电源工作容量，从而使得剩余负荷尽可能保持平稳，以减少因火电调峰容量不足导致的水电调峰弃水电量[17]。与常用的逐次切负荷法不同，余荷逐次后移法无需循环寻找工作位置，直接通过公式求得电站最大工作容量和全时段的负荷分配情况，计算量较小。

2.3 算法耦合

负荷分配、检修计划、备用配置是电力电量平衡计算中不可缺少的3个部分。在常规算法中，通常针对某一方面进行优化，其他两方面则是按既定规则设置，如此使得电力电量平衡结果比较片面。若考虑检修、备用和负荷分配，对模型进行优化，则须采用耦合智能算法。故本文提出，利用分布估计算法分配检修容量，逐次逼近算法分配备用容量，将两种算法进行耦合，可以全面有效地进行电力电量平衡计算。

耦合算法是以分布估计算法为基础，建立种群，随机生成满足检修约束的检修计划；将逐次逼近算法嵌入分布估计算法，在个体检修计划固定的情况下对每个种群个体的备用方案初始解进行寻优；将各个电站除去备用容量和检修容量后的最大工作容量带入余荷逐次后移法中，计算弃水电量，作为个体的适应度，判断种群个体的优秀程度；选择精英个体，分析各个电站检修计划的概率分布，并按概率生成下一代个体。具体步骤如下。

(1)生成随机初始种群。种群个体X有两部分组成，如式(15)，分别是i电站各时段检修机组台数和各时段所承担的备用容量。

(15)

各电站的检修计划随机生成，承担的备用容量则是在解空间范围内随机生成，如式(16)：

(16)

(2)对个体的备用容量进行逐次逼近算法寻优，通过余荷逐次后移法进行负荷分配，并计算决策变量，即日弃水电量，作为逐次逼近算法的寻优方向。月弃水电量和典型日弃水电量的转化通过电站月调节系数进行，其为电站典型日平均出力与月平均出力之比，代表月内用电的不均匀性。

(17)

完成寻优后，得到每个个体在固定检修容量的情况下，备用分配最优方案。各月弃水电量求和即可得到种群个体在检修已定的情况下最优年弃水电量，将弃水电量作为种群个体的适应度。

(3) 判断种群中最优个体的年弃水电量最小值是否收敛，或弃水电量为0，或代数达到要求。若满足上述任一条件则终止寻优，输出结果；否则，转至步骤(4)。

(4)对比种群中个体的弃水电量，按一定比例挑选精英个体，组成精英集，分析精英集中各个电站检修容量、各月备用容量的概率分布，按照概率分布随机生成下一代种群个体中检修和备用部分。在下一代种群生成过程中，加入随机变异因子，即对精英集检修容量的概率分布，按一定比例进行随机修正，使得算法迭代后期具有跳出局部最优的能力，防止因陷入局部最优而过早收敛。完成后转至步骤(2)。

3 算例分析

3.1 基本信息

以某区域电网为例，其枯水年的汛期为6-9月，其余月份为非汛期。1-12月月最大负荷、月平均负荷如表1所示，汛期与非汛期各月典型日负荷率如表2所示。电力系统中的12座水电站枯水年月平均出力如表3所示，12座水电站和1座火电站的详细资料如表4所示，系统的总装机为21 050 MW。

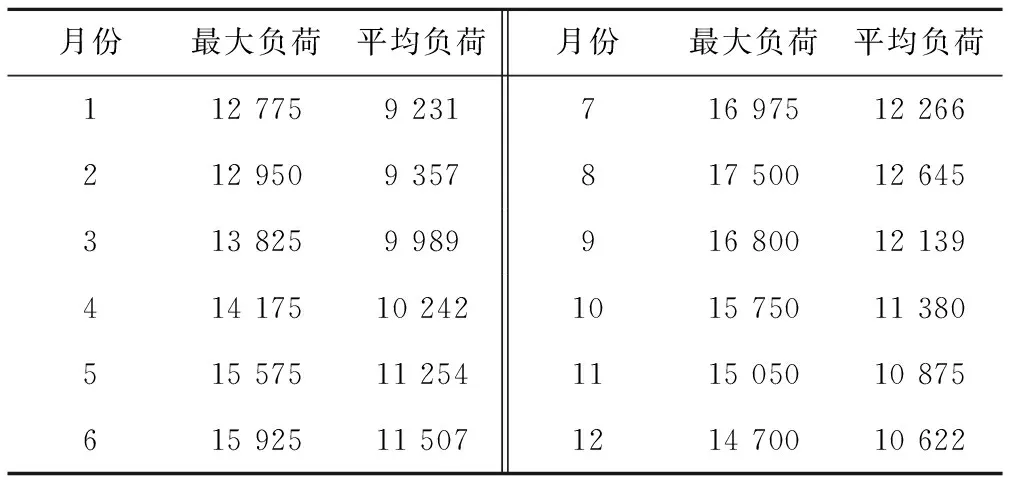
表1 电力系统年最大负荷 MW

表2 电力系统汛期和非汛期典型日负荷率Tab.2 Typical load rate of a power system in flood season and non-flood season

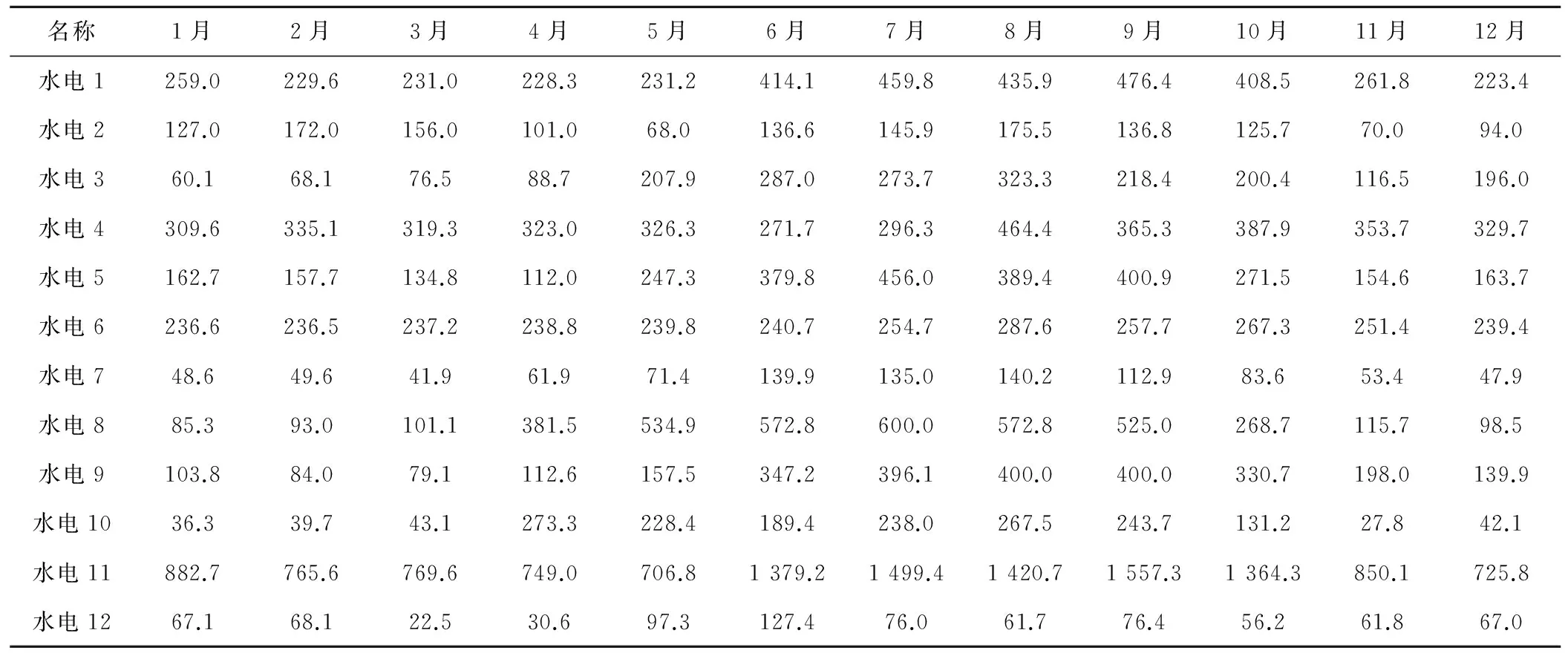
表3 电力系统水电站月平均出力 MW

表4 电力系统电站基本信息Tab.4 The basic information of all stations in a power system

本算例中，电力系统备用容量为年最大负荷的10%，火电站月调节系数为1.05，所有机组检修时间为1个月。

3.2 电力系统电力电量平衡结果分析

算法参数部分，分布估计算法的循环代数为40代，种群个数为60，每代的变异系数为0.01/Gen，Gen为代数；逐次逼近算法中，每个电站离散点为30个(包括初始点)。

3.2.1 算法效率分析

耦合算法中的逐次逼近部分涉及对备用容量区间的离散，离散点的个数必然影响算法的计算效率。当火电调峰系数为0.2时，计算结果如表5所示。离散点由30增加至50时，计算时间增加1倍，但优化结果的相对变化只有0.12%。所以离散点个数不宜过多，根据实验结果，建议选择30个离散点。

3.2.2 火电调峰系数敏感性分析

火电调峰系数是模型不确定性的来源，也是导致弃水电量的主要因素之一，故有必要对火电调峰系数进行敏感性分析。火电调峰系数从0.2到0.5，弃水电量结果如表6所示。随着火

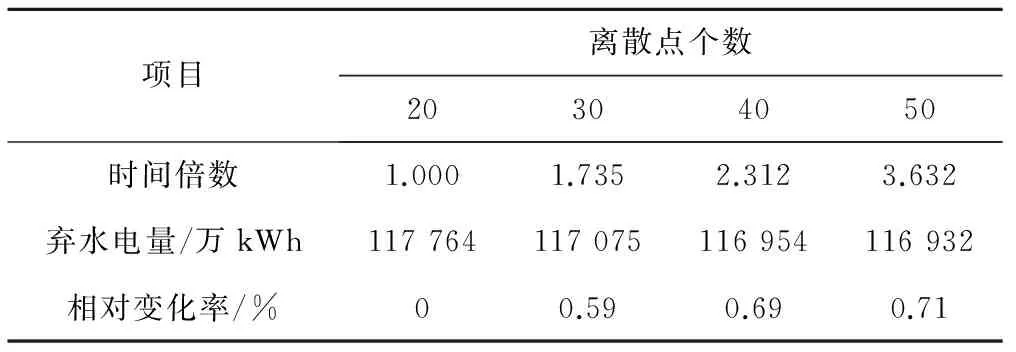
表5 离散点个数与计算效率分析Tab.5 Analyses of the number of discrete pointsand the calculation efficiency

表6 弃水电量与火电调峰系数变化Tab.6 Abandoned hydropower and thermal peak-shaving coefficient

电调峰系数的增加，弃水电量快速减少。在火电比重较大电网中，为满足电网调峰需求，火电需要0.5～0.6的深度调峰，影响了调峰机组的经济性；但在水电比重较大的电力系统中，水电一般配合火电进行调峰，且调峰成本相对火电来说可以忽略不计[18]，火电减少参与深度调峰，故调峰系数通常较低。火电调峰系数为0.2时，弃水电量大，其电力电量平衡结果更具有深度分析价值，所以本文的后续分析中，火电调峰系数采用0.2。

3.2.3 算法收敛性分析

采用耦合算法重复计算30次，得到的弃水电量最优值中，最大为118 595 万kWh，最小为116 732 万kWh，平均值为117 394 万kWh，离散系数为0.003 4，算法具有较好的稳定性。

对其中任意一次计算结果进行分析。在经历40代寻优迭代后，得到系统年弃水量最优值为117 050 万kWh。种群收敛过程如图2所示。从最优结果变化中可以看出，算法在15代左右趋于收敛，稳定在118 863 万kWh左右。由于在设计分布估计算法时，为防止过早陷入局部最优，未将每代最优个体直接加入下一代，下一代的种群是完全通过上一代的精英个体的概率分布随机生成的，故最终结果无法收敛在固定最优值上，而是在小范围内波动。

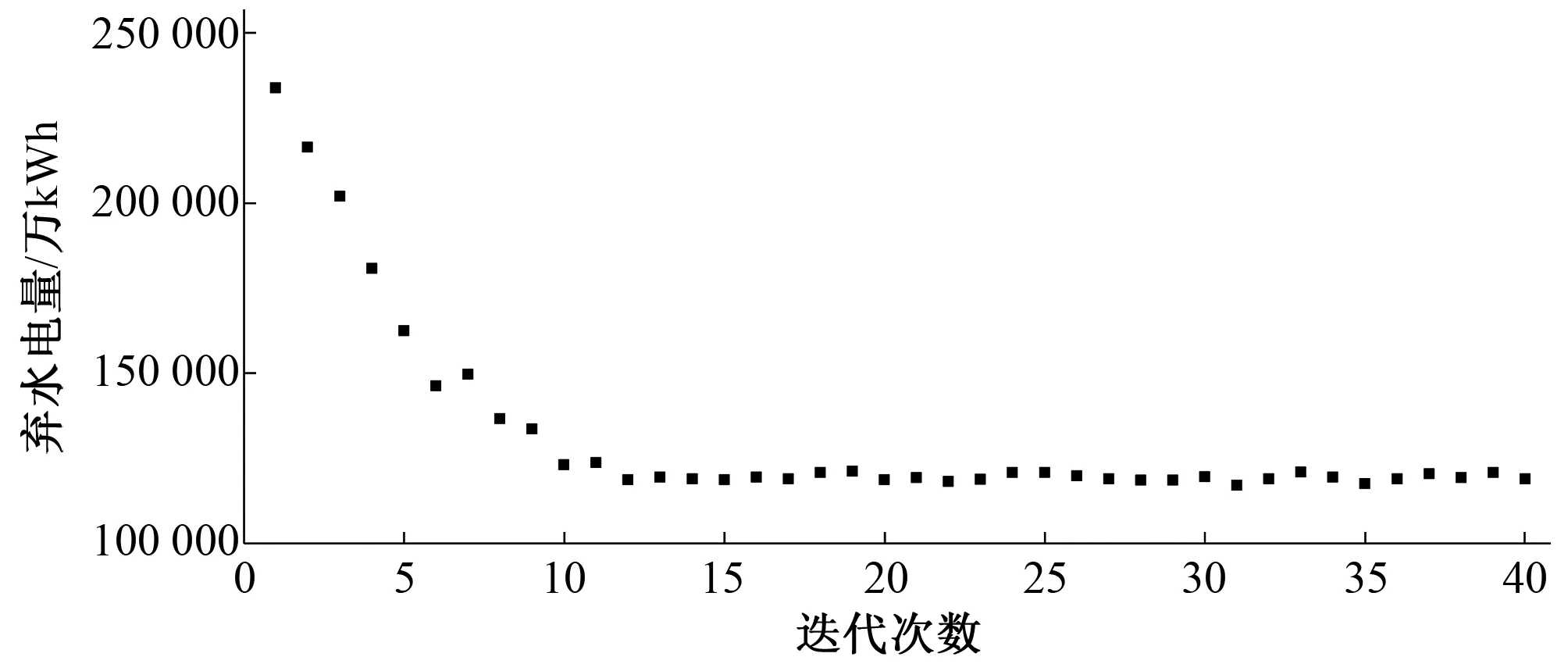
图2 算法收敛过程图Fig.2 Algorithm convergence procedure chart

3.2.4 电力电量平衡结果分析

对弃水电量最优个体进行分析，年电力平衡图如图3所示，年电量平衡图如图4所示。

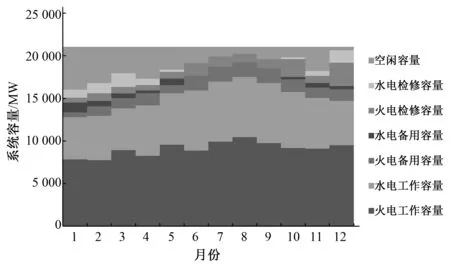
图3 最优弃水电量下年电力平衡图Fig.3 Annual balance of electric power of the optimum individual

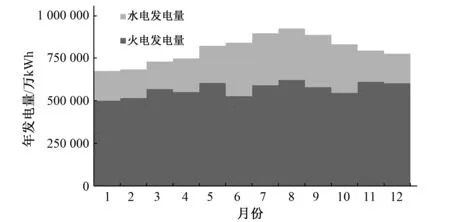
图4 最优弃水电量下年电量平衡图Fig.4 Annual balance of electric energy of the optimum individual

检修分配：水电站的检修集中在非汛期，汛期未安排水电检修，即水电月平均出力较小的月份，此时安排适当检修容量不会影响到水电站正常发电，不会因工作容量不足而产生弃水电量。火电的检修分布在全年，在汛期同样存在火电检修，在火电空闲容量较大的月份安排适当检修并不会影响到火电的最大出力值，不会因此改变火电调峰容量上限，水电并不会产生额外的调峰弃水。

备用配置：在非汛期，火电和水电都有承担备用容量，水电因发电量较少而有较好的调峰能力，水电承担备用容量虽然会削减水电的调峰能力，但不会影响水电正常发电，也不会使火电超出调峰限制；在汛期，水电月平均出力接近水电装机容量，承担备用容量势必产生额外的弃水电量。

出力过程分析：从12个月的出力过程中找到两个有代表性的月份，非汛期2月与汛期8月，其各电站出力过程如图5和图6所示，火电站各月调峰比例如表7所示。在枯水期，水电承担了所有的峰荷和部分腰荷，而给火电留下了基荷和部分腰荷，这与逐次后移法优先采用调峰能力强的电站填补负荷图的峰荷的性质有关，留给火电承担的负荷已经通过水电的调峰作用变得相对平稳，火电调峰产生的弃水降到了最低。在汛期，水电月平均出力大，调峰能力较弱。完成水电切负荷后，留给火电的负荷仍有较大的峰谷差，为了满足火电调峰容量限制，提高火电基荷出力位置，水电被迫弃水提高调峰能力。算例中，设置的火电调峰限制为20%，从表7可以看出，在优化计算检修和备用后，在汛期火电调峰达到上限，说明汛期弃水电量主要由是调峰产生的。

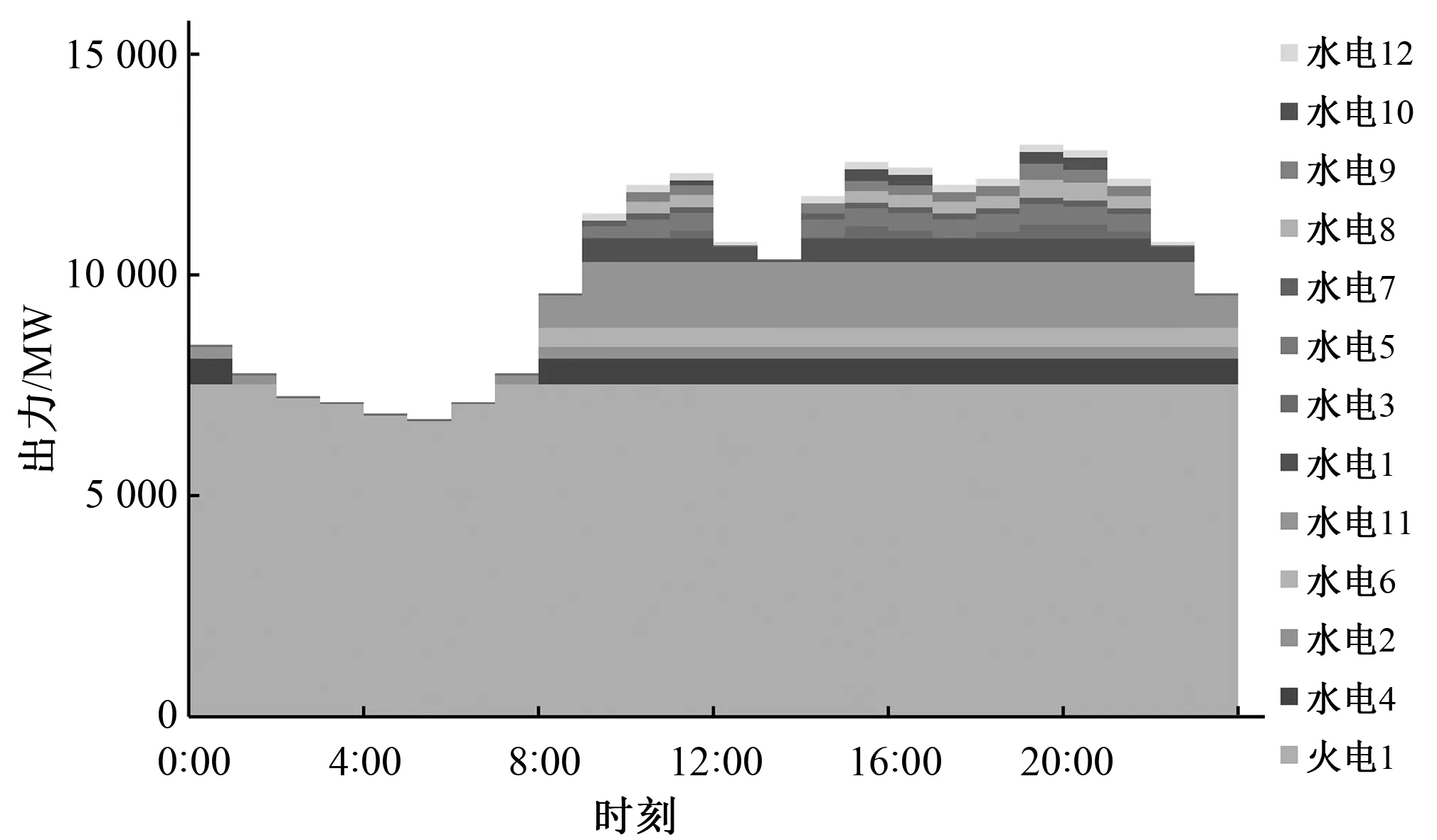
图5 2月典型日出力过程图Fig.5 Typical daily output process in February

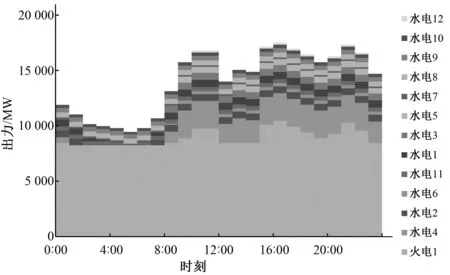
图6 8月典型日出力过程图Fig.6 Typical daily output process in August

%

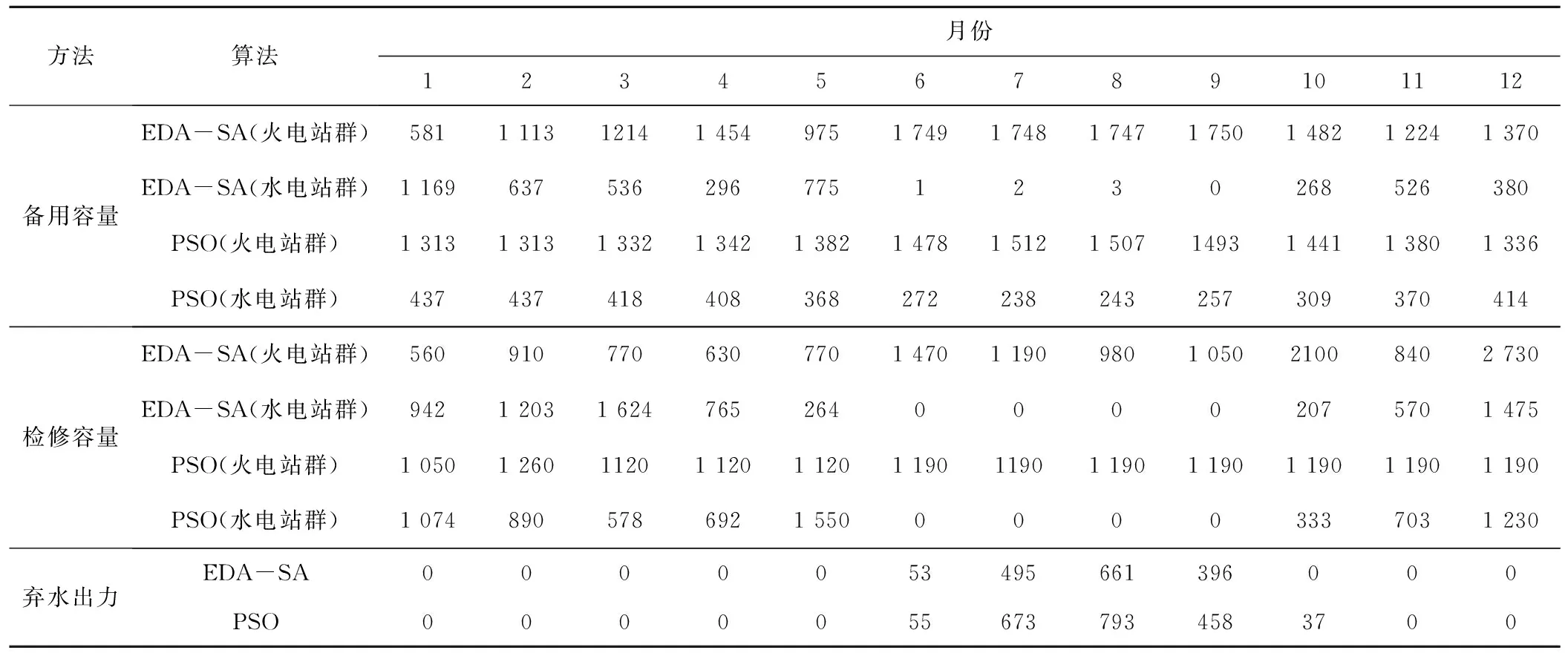
表8 EDA-SA与PSO算法结果对比 MW

非汛期，因为水电检修和备用的合理分配，未出现水电最大工作容量无法达到理论出力的情况，水电发电量全部被电网消纳，未产生弃水电量。

由于备用和检修是在不同时空维度上的优化，目前，尚未有同时考虑备用优化和检修优化的方法，常用的是通过智能算法优化检修，备用按一定规则分配。所以采用粒子群算法优化检修、按装机比例分配备用容量，设计对比方案。经计算，对比方案年弃水电量为147 087 万kWh。将其结果与耦合算法进行对比，如表8所示，表8的各月弃水电量用等效的月弃水平均出力来表示。从表8可以看出，耦合算法在汛期由火电承担全部备用，而对比方案则是水电、火电共同承担全部备用；同时对比方案的水电检修过程与耦合算法得到的过程类似，都是非汛期安排检修，在汛期未安排水电检修，但对比方案的火电检修接近于全年平均分配，而耦合方法得检修则有针对将火电检修向部分月份集中。由此可得，耦合算法在汛期产生较少弃水，而在非汛期不产生弃水，得到全年总弃水电量优于对比方案。

分别固定算例中耦合算法的检修计划和备用配置，作为约束条件，采用粒子群算法，对检修计划和备用容量进行寻优计算，以验证算法对单一对象的寻优能力。反复计算10次，两种方案弃水电量结果如表9所示。两种方案的结果与耦合算法结果几乎相同，耦合算法对单个对象的寻优已达到最佳水平。

该算例表明，在汛期，水电承担备用容量会造成大量弃水，备用容量应尽量由火电承担；同时，在汛期水电出力较大，火电存在较多空闲容量，可以适当安排火电检修，减小火电在非汛期的检修压力，从而增大火电非汛期调峰容量，减小非汛期弃水电量。

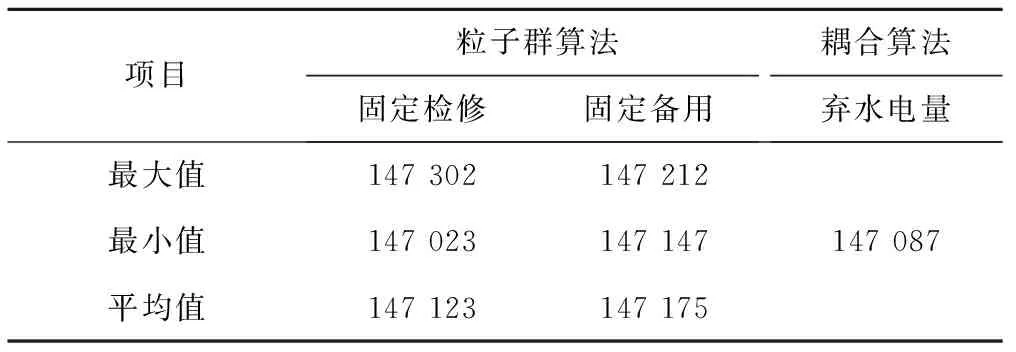
表9 单一优化对象下PSO与EDA-SA结果对比 万kWh

4 结 语

本文以弃水电量最小为目标建立优化模型，以检修计划和备用配置作为优化对象，并提出了分布估计-逐次逼近耦合算法(EDA-SA)，实现了对模型的求解。实例表明，EDA-SA算法对弃水电量模型求解效果较好，能够解决检修和备用在不同时间维度上的优化问题，和单一优化方法相比，EDA-SA算法可以降低电力系统弃水电量，得到合理的电力容量配置方案。

□

参考文献：

[1] 吴东平，杨 强．弃水电量的成因分析计算法[J]．水力发电，2014，40(12)：71-74．

[2] 刘 方，张粒子．考虑日前调峰分配和流量波动平抑的梯级水电双层优化调度[J]．电网技术，2017，41(3)：799-807．

[3] 乔 娟，张立仁，姚 涛. 某地区小水电增效扩容改造方案及评价[J]. 中国农村水利水电，2013，(6)：153-155.

[4] 张 今．水电弃水电量跨省消纳的定价方法研究[J]．中国农村水利水电，2016，(7)：175-179．

[5] 蒲天骄，陈乃仕，葛贤军，等．电力电量平衡评价指标体系及其综合评估方法研究[J]．电网技术，2015，39(1)：250-256．

[6] 廖胜利，程春田，蔡华祥，等．改进的火电调峰方式[J]．电力系统自动化，2006，(1)：89-93．

[7] 吴东平，万永华．日电力电量平衡的余荷逐次后移法[J]．水力发电学报，1994，(3)：31-36．

[8] 庞 峰．电力电量平衡新方法[J]．水力发电学报，2001，(4)：117-123．

[9] 白 杨．山东电力系统发电机组检修计划优化研究[D]．济南；山东大学，2008．

[10] 曾 莹．基于层次分析法及改进遗传算法的设备检修计划优化[D]．北京：华北电力大学，2011．

[11] 刘文颖，谢 昶，文 晶，等．基于小生境多目标粒子群算法的输电网检修计划优化[J]．中国电机工程学报，2013，33(4)：141-148．

[12] 贺 辉，姚建刚，欧阳永熙．负荷参与备用市场的讨论[J]．电力自动化设备，2002，(7)：66-68．

[13] Yu C W，Zhao X S，Wen F S，et al．Pricing and procurement of operating reserves in competitive pool-based electricity markets[J]．Electric Power Systems Research，2005，73(1)：37-43．

[14] 陶晓龙．弃水电量计算模型的研究[D]．北京：华北电力大学，2014．

[15] 孙新德．华中电网水电弃水损失电量计算方法探讨及对策[J]．华中电力，2001，(2)：38-40．

[16] 周树德，孙增圻．分布估计算法综述[J]．自动化学报，2007，(2)：113-124．

[17] 程春田，李建兵，李 刚．水电站分段调峰负荷分配方法研究与应用[J]．水力发电学报，2011，30(2)：38-43,132．

[18] 谢 俊，张晓花，吴复霞，等．基于合作博弈论和工程方法的调峰费用分摊[J]．电力系统保护与控制，2012，40(11)：16-23．