基于鲸鱼优化算法的水资源优化配置研究

李新德，沙金霞，刘 彬，闫志宏，李 苏，周伟凯

(河北工程大学水利水电学院，河北 邯郸 056038)

1 研究背景

我国水资源短缺问题突出，特别是华北平原地区，地下水超采严重，供需矛盾突出。为了解决区域水资源短缺问题，近年来对水资源优化配置的研究成为了一个热门课题，水资源优化配置指在一个特定区域或流域内，对不同形式的有限水资源进行科学合理的分配。水资源优化配置是一个受多目标控制的问题，目标通常包括经济效益、社会效益和生态环境效益等多种。通过水资源优化配置达到对区域有限水资源的合理分配，为区域内各用水部门提供可靠水源，使各用水部门达到供需水量平衡，实现水资源可持续利用。

目前我国对于水资源优化配置方法的研究正逐步趋于成熟，并处于不断地改进和完善的过程[1]，受到学术界的广泛关注，尤其是近年来提出的新型仿生智能算法，如粒子群优化(PSO)算法[2]、多目标遗传算法[3]、改进的人工鱼群算法[4]、蚁群算法[5]等，这些算法均在一定程度上解决了水资源优化配置方面的问题，但仍存在收敛速度慢和局部寻优等缺点。本文把一种新型的仿生智能算法：鲸鱼优化算法[6](Whale Optimization Algorithm，简称WOA)引进到水资源优化配置中，利用鲸鱼优化算法参数调节少、收敛速度快和全局寻优能力强等特点，成功将其与水资源优化配置问题进行结合。并以邯郸市东部平原区为例，以经济效益和社会效益最优为目标，构建水资源优化配置模型，利用鲸鱼优化算法求解出邯郸市东部平原区在规划水平年(2020年)不同保证率下的水资源优化配置方案，旨在实现邯郸市东部平原区内各用水部门水资源的合理、充分利用，使该区域的社会、经济、资源等方面得到协调发展[7]。

2 鲸鱼优化算法

鲸鱼优化算法(whale optimization algorithm，WOA)是一种新型群体智能优化算法，由澳大利亚学者Mirjalili和Lewis于2016年提出[8]，该算法受自然界座头鲸的觅食行为的启发，对座头鲸群体的收缩包围、螺旋式位置更新和随机捕猎机制进行模拟。该模型共包括环绕式捕食、泡泡网捕食和搜索捕食3个阶段[9,10]。

2.1 环绕式捕食

在环绕式捕食中，座头鲸能识别猎物的位置并对猎物进行包围，由于搜索空间中的最优解的位置是预先不可知的，因此WOA优化算法假设当前最优位置为目标猎物。在定义了最优位置之后，其他鲸鱼个体会尝试将它们的位置向最优位置更新。此行为由下式表示：

(1)

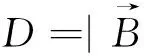
(2)

(3)

(4)

a的变化情况见下式：

(5)

式中：tmax为最大迭代次数。

2.2 泡泡网捕食

为了用数学模型模拟座头鲸的泡泡网捕食行为，设计了如下两种机制：收缩包围机制和螺旋更新位置机制。

(1)收缩包围机制。通过减小控制参数a，从而减小随机变量A，随机变量A的取值范围是[-a,a](a从2线性减小到0)，把随机变量A的取值范围设置在[-1,1]时，鲸鱼个体的新位置可以定义在原始位置和当前位最优位置之间的任何位置，其数学模型由式(1)和式(2)表示。

(2)螺旋更新位置机制。在螺旋更新位置机制中，首先计算鲸鱼和猎物(当前最优解)之间的距离，然后在鲸鱼和猎物(当前最优解)的位置之间建立一个对数螺旋方程来模拟座头鲸的螺旋形运动，其数学模型如下:

(6)

(7)

式中：D′为第i只鲸鱼和猎物(当前最优解)之间的距离；b为控制对数螺线形状的常数；l为一个[-1,1]之间的随机数。

这里需要注意的是，鲸鱼在攻击猎物时，在收缩包围的同时，也在沿着螺旋形路径运动。为了模拟该行为，在优化过程中，假设收缩包围机制和螺旋位置机制的更新概率相同，均为0.5。所以构建数学模型如下：

(8)

式中：p为一个[0,1]的随机概率。

2.3 搜索捕食

实际上座头鲸在捕食过程中，鲸群个体会根据彼此的位置进行随机搜索猎物，该捕食方式称为搜索捕食。搜索捕食与环绕式捕食基于的方法相同，都是通过改变变量A的大小来搜索猎物的，在搜索捕食中，设定系数变量|A|≥1，迫使鲸鱼个体远离参照鲸鱼，来寻找其他更合适的猎物。与环绕式捕食不同的是，该阶段不是根据当前获得的最优个体，而是根据随机选择的鲸鱼个体作为参照鲸鱼来更新其他鲸鱼个体的位置。这种算法设定了系数变量|A|≥1，以增强算法的搜索捕食能力，使该算法能在全局范围内进行搜索。其模型可表示为：

(9)

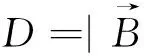
(10)

2.4 鲸鱼优化算法在水资源优化配置中的应用

利用鲸鱼优化算法求解水资源优化配置问题的基本思路：先确定优化配置问题中的决策变量，本文以各水源分配给各用户的可供水量作为决策变量；然后初始化鲸鱼种群，随机生成 个鲸鱼，鲸群中每个个体所处空间位置均代表一组决策变量；通过目标函数来确定每个鲸鱼个体所处空间位置的优劣，利用鲸群的不同形式的觅食策略不断更新当前鲸鱼个体的空间位置，如此反复迭代直至获得最优鲸鱼的空间位置，即为该优化配置问题的最优解。其具体求解步骤如下。

步骤4：检查是否有任何鲸鱼个体更新后的位置超越了搜索空间(约束条件)，对超越搜索空间的鲸鱼位置进行修正。

3 实例分析

3.1 研究区概况

邯郸市东部平原区位于北纬36°06′～36°57′，东经114°24′～115°29′之间，总面积7 587 km2，主要包括邯郸县、永年县和磁县部分以及除涉县、武安市、峰峰矿区以外的其他地区，具体位置见图1。目前邯郸市东部平原区存在着众多水资源问题：东部平原区属于资源型缺水地区，研究区现状年2015年可供水量为17.194 57 亿m3，需水量为23.921 27 亿m3，全区缺水量为6.702 7 亿m3。由于水资源量匮乏和不合理的用水制度，使得区域内各用水部门的供需矛盾逐年增加，工农业争水矛盾日益突出，迫使大量开采地下水，导致整个区域地下水超采情况严重，为了解决东部平原区面临的一系列水资源问题，利用鲸鱼优化算法对东部平原区水资源进行合理配置。

图1 邯郸市东部平原区位置图Fig.1 Location map of the eastern plain area of Handan city

3.2 子区的划分及水源、用户组成

本次邯郸市东部平原区水资源优化配置模型子区的划分主要基于邯郸市行政分区，将东部平原区划分为14个子供水区域，每个子区水源既包括公共水源(引江水、引黄水、东武仕水库水、岳城水库水和卫河水等)又包括独立水源(自产地表水、地下水和再生水等)；每个子区的用水户分别由生活用水、工业用水、农业用水和生态环境用水4部分组成。

深入分析各子区之间、各子区与不同水源、水源与用水户之间的联系，构建邯郸市东部平原区水资源优化配置系统网络图。主要包括：各子区之间的联系、各子区与水源之间的联系和各子区内水源与用户之间的联系等，构建的系统网络图如图2所示。

3.3 优化配置模型

3.3.1 目标函数

对于构建目标函数，在水资源优化配置中主要包括区域社会效益最优(总缺水量最小)、区域经济效益最优、区域环境效益最优等。本次优化配置主要解决邯郸市东部平原区水资源匮乏所引起的一系列问题，以及此次优化配置为多水源联合调度，丰平枯水年联合调节，涉及区域广、用水户多。因此本文主要选取了经济效益最优和社会效益最优作为目标来构建目标函数，构建结果如下。

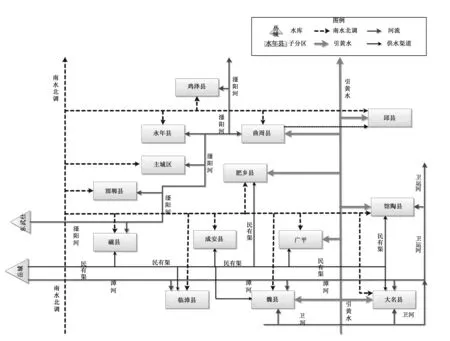
图2 邯郸市东部平原区水资源优化配置系统网络图Fig.2 Network map of water resources optimization allocation system in the eastern plain area of Handan city

(1)经济效益最优。本次优化配置既考虑公共水源供水量又考虑了独立水源供水量，以两者供水产生的净效益之和来表示该区域的经济效益，构建的经济效益目标函数如下：

(11)

(2)社会效益最优。由于将社会效益作为目标度量难度大，因此本研究以区域总缺水量最小来作为社会效益的量化指标，使得公共水源和独立水源的供水量能够充分满足用户的用水需求，其计算公式为：

(12)

3.3.2 约束条件

(1)区域供水能力约束。要求k子区独立水源和公共水源供水量不得超过该区域的可供水量，即：

(13)

(14)

(2)输水系统的输水能力约束。

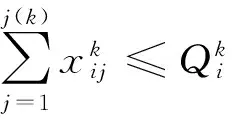
(15)

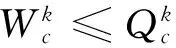
(16)

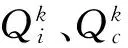
(3)用户需水量约束。要求k子区独立水源和公共水源供水量之和介于用户最小需水量和最大需水量之间，即：

(17)

(4)非负约束。要求独立水源和公共水源的供水量均不小于0，即：

(18)

4 结果分析

由上述优化配置模型分别计算邯郸市东部平原区规划水平年(2020年)不同保证率(P=25%、50%、75%)下的水量优化分配方案。邯郸市东部平原区需水量主要分为生活需水量、工业需水量、农业需水量和环境需水量等，采用定额法预测东部平原区2020年不同保证率下14个子区的需水量，不同保证率下的需水预测结果见表1。邯郸市东部平原区主要供水水源分为地表水、地下水、外调水和再生水，2020年不同保证率下可供水量预测结果见表2。

表1 2020年不同保证率下需水量预测结果 万m3

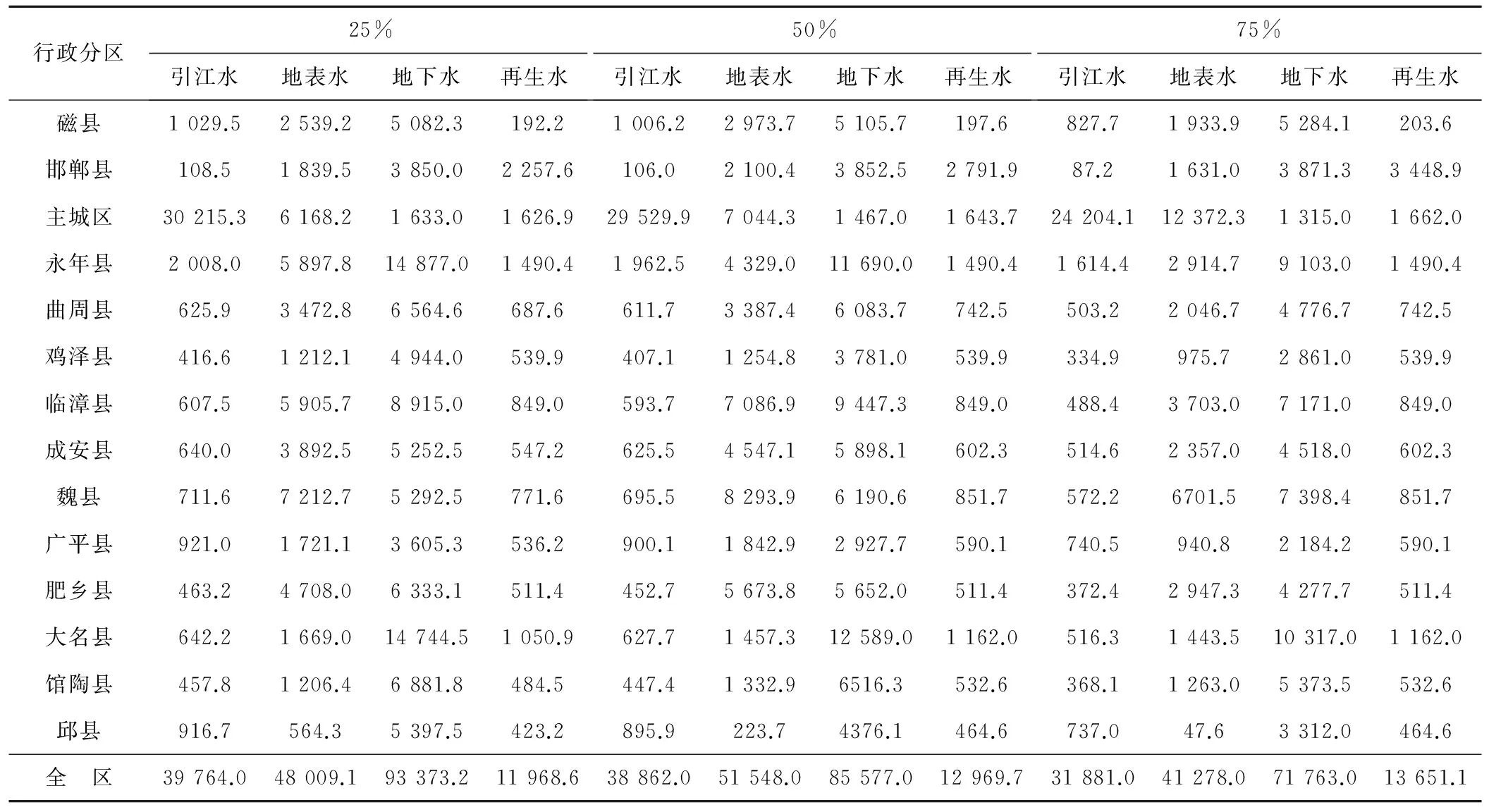
表2 2020年可供水量预测结果 万m3

邯郸市东部平原区经济效益最优和社会效益最优两个目标函数采用加权法：其中经济效益权重0.4，社会效益权重0.6。目标函数系数确定：引江水、地表水、再生水、地下水，选取供水次序系数依次为0.4、0.3、0.2、0.1；其次确定用户公平系数，本次确定邯郸市用户得到供水的次序依次为生活用水、工业用水、环境用水、农业用水，选取用户公平系数依次为0.4、0.3、0.2、0.1；供水费用系数的确定，根据邯郸市最新水价确定，城镇居民生活用水费用系数取4.22 元/m3，农村居民生活用水费用系数取1.20 元/m3，工业用水费用系数取4.85 元/m3，农业灌溉用水费用系数取0.38 元/m3，环境用水费用系数取1.80 元/m3；用水效益系数中工业用水效益系数为工业用水定额的倒数，取500 元/m3，生活用水效益系数取600 元/m3，环境用水效益系数取600 元/m3，农业灌溉用水效益系数取15 元/m3。

模型的计算参数选择如下：取鲸鱼种群数目N=100；最大迭代次数tmax=1 000；控制参数a取值范围从2到0线性减小。

规划水平年不同保证率下水资源优化配置计算结果见表3～表5。由表3～表5可知，该优化配置结果在规划水平年不同保证率下在充分合理利用外调水、地表水、再生水和地下水的情况下，一定程度上缓解了各地区各部门的用水矛盾：在25%保证率下，仅永年县和鸡泽县仍处于缺水状态；在50%保证率下，除磁县、邯郸县、主城区、临漳县、成安县和魏县外，其他地区仍有不同程度的缺水；在75%保证率下，经过配置后，各地区均有不同程度的缺水。结果表明东部平原区属于资源型缺水地区，只有加强开源节流，并提高人们的节水意识，建立节水型社会，并进一步加大外流域调水，才能更好地解决水资源短缺问题。

表3 2020年25%保证率水资源优化配置结果 万m3

表4 2020年50%保证率水资源优化配置结果 万m3

表5 2020年75%保证率水资源优化配置结果 万m3

5 结 语

本文采用鲸鱼优化算法对水资源优化配置进行研究，并依据相应的目标函数及约束条件建立优化配置模型，对邯郸市东部平原区水资源进行合理配置。此次配置在 一定程度上缓解了研究区丰水年和平水年的用水紧张形势及各用水部门的用水压力，但枯水年各地区各用水部门仍处于水资源短缺状态。经实例分析，鲸鱼优化算法作为一种新型优化算法化，具有参数调节少、收敛速度快和全局寻优能力强等优点，在水资源优化配置方面具有良好的应用前景，并对优化算法提出一种新的求解思路。

□

参考文献：

[1] 陈太政，侯景伟，陈 准.中国水资源优化配置定量研究进展[J].资源科学,2013,35(1):132-139.

[2] 裴 浩，袁 刚，唐 勇，等.基于粒子群算法的邯郸市水资源优化配置系统研究[J].水科学与工程技术,2011,(3):8-10.

[3] 陈南祥，李跃鹏，徐晨光.基于多目标遗传算法的水资源优化配置[J].水利学报,2006,37(3):308-313.

[4] 李 苏，刘 彬. 改进的人工鱼群算法在邯郸市水资源优化配置中的应用[J].水电能源科学,2016,34(12):10-14.

[5] 刘玒玒，汪 妮，解建仓，等.基于蚁群算法的水资源优化配置博弈分析[J].西北农林科技大学学报,2012,42(8):205-211，220.

[6] 崔东文.鲸鱼优化算法在水库优化调度中的应用[J].水利水电科技进展,2017,37(3):72-76,94.

[7] 高 佳.邯郸市东部平原区水资源优化配置研究[D]. 河北邯郸：河北工程大学,2009.

[8] Seyedali Mirjalili, Andrew Lewis.The Whale Optimization Algorithm[J]. Advances in Engineering Software, 2016, 95:51-67.

[9] Majdi M.Mafarja, Seyedali Mirjalili.Hybrid Whale Optimization Algorithm with simulated annealing for feature selection[J]. Neurocomputing, 2017,260:302-312.

[10] Mohamed Abd El Aziz, Ahmed A Ewees, Aboul Ella Hassanien.Whale Optimization Algorithm and Moth-Flame Optimization for multilevel thresholding image segmentation[J]. Expert Systems with Applications, 2017,83:242-256.