基于一卡通数据的高校学生行为分析与排名预测

甘伟

（四川大学计算机学院，成都 610065）

0 引言

校园一卡通的系统是数字化校园建设中必不可少的组成部分和基础工程[1]。随着计算机应用技术和数据库安全技术的发展，校园一卡通在各大、中、小学中都有广泛的应用。其中，大学生的校园一卡通的系统最为成熟，业务覆盖范围最广，所涉及的业务包括就餐、消费、门禁、交通、打印等，且呈现逐年增长的趋势。一个大学在校人数一般为几千甚至几万人，每天产生大量的一卡通数据[2]。而在这些庞大的数据记录中就隐含着在校大学生的消费水平、行为规律等[3]。校园一卡通所记录的数据被越来越多的人关注，其重要的原因就是这些数据可以在一定程度上反映在校大学生的一些情况。因此，有很多研究人员对学生的消费记录做出分析，用来分析学生的消费水平、为学校后勤部门提供决策依据。

但是目前对一卡通数据的研究大部分都是通过一些统计的方法研究一卡通的某些类型的数据，极少有研究人员结合可视化技术[4]交互手段对一卡通所记录的信息进行全面分析或展示的。本文中采用了可视化技术对一卡通数据进行全面展示，以图表的形式直观地帮助用户理解数据、发现数据中隐藏的规律[5]，帮助用户分析学生行为。

1 可视化效果展示及分析

本文对数据的展示与分析主要利用了三个视图。整个界面如图1所示，主要分为用螺旋视图[6]表示的学生行为视图，用圆圈表示的学生信息视图和用堆叠条形图表示的学生消费视图。

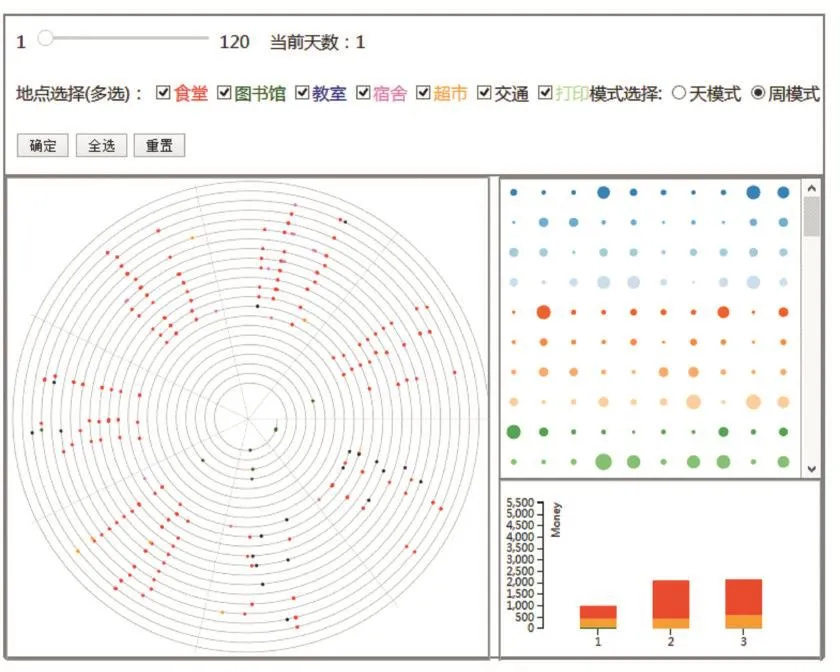
图1 总视图

1.1 学生行为视图

学生行为视图展示的是学生在什么时间、什么地点发生了某些特定的行为，这些行为主要包括在食堂就餐、到超市购物、图书馆购物、教室消费、寝室消费、打印、乘车等。图2（a）为螺旋视图在“周模式”时的展示情况，用来显示每个学期学生的一卡通数据记录，每一圈表示的是一周的一卡通数据记录，通过用户交互可以选择感兴趣的记录类型或模式。图2（b）为“天模式”下的展示情况，用来显示某连续9天的一卡通数据记录，每一圈表示的是一天的一卡通数据记录，和在“周模式”下有同样的交互。两种模式的不同之处在于“天模式”可以对所要展示的时期通过滑动条来选择，每次展示的只是某个学期的部分数据，而且在数据映射上用圈的大小代表消费金额的多少。

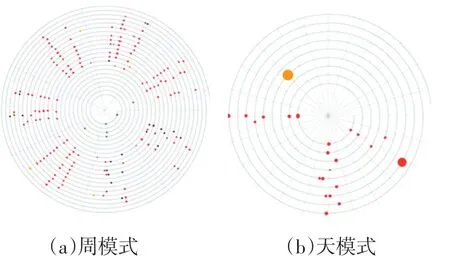
图2 不同模式下的学生行为

1.2 学生消费视图

如图3（a）所示，展示的是用堆叠条形图表示的学生消费视图，用来展示每个学期的消费总金额以及各类消费金额（颜色与螺旋视图的映射方案一致）。可以看到每个学期的消费以食堂消费为主，其次是超市。二三学期的学费总金额和各项消费金额变化不大，都和第一学期的消费有较大的差异。图3（b）是用一个圆圈来展示一个学生信息，用来展示学生及成绩相关信息，颜色不做任何映射。每个圆圈的大小表示该学生跟上学期相比成绩变化的大小。当鼠标悬浮在某个圆圈上时，所有圆圈的颜色会发生变化，红色的表示学生上学期排名上升，蓝色表示该学生上学期排名下降。

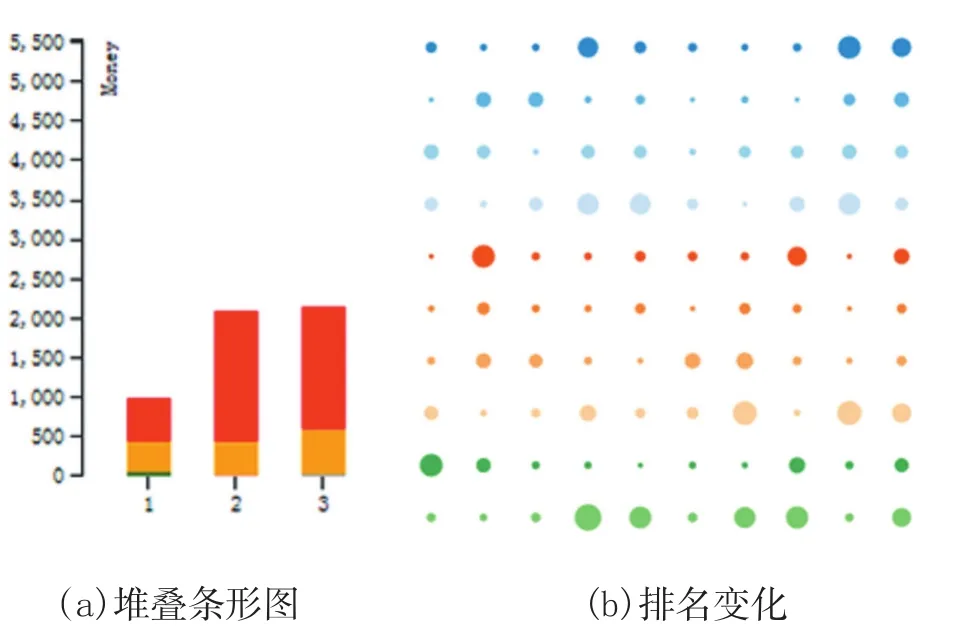
图3 不同模式下的学生行为

2 基于多元线性回归算法的学生成绩排名预测

2.1 特征提取

本文先以可视化的方式来展示一卡通数据，通过交互操作发现学生去图书馆的次数、有无早起吃早饭的习惯、进图书馆的次数以及借书的数量对学生成绩有较大的影响。因此，本文选取了以上的几个特征来对学生的相对排名做出预测。

在第一次实验中，利用第一学期的相对排名和第二学期该学生去图书馆的次数、吃早饭的次数（十点之前有食堂刷卡记录视为早饭记录）、借书的数量这些变量为特征训练出一组参数。在利用这组参数和第二学期的排名、第三学期的同样的特征预测第三学期的相对排名时，发现效果并不是很好。分析其原因，在利用可视化试图分析学生行为时，是依据学生两个学期行为的变化来预测学生成绩的升降的。每个学生的学习行为本身就具有很大的差异性，所以根据学生单个学期的表现就判断该学生成绩的变化是没有意义的，而依据学生在学习行为上的变化（在本文中主要是指和上学期相比产生的差异）来判断学生成绩的变化才是有意义的。根据以上分析，又重新选择了特征，重新选择的特征为上学期的相对排名、和上学期相比进图书馆增加的次数、吃早饭增加的次数、借书增加的数量（表 1）。

表1 特征表

2.2 成绩排名预测结果

线性回归是运用统计学的方法，来分析自变量和因变量之间的依赖关系，并依据这种关系进行建模的回归分析。这种模型是目前应用的非常广泛的预测模型。在线性回归模型中，自变量和因变量是一种线性关系。依据人们的经验，上学期的成绩、本学期的行为表现和本学期的学习成绩之间是一种线性关系。例如，去图书馆的次数少了，可能成绩就有所下降，去图书馆的次数变得越少，成绩可能就退步得越多。本文选取了四个特征及存在四个自变量，来预测学生相对排名。因为，存在两个以上的自变量，所以使用的回归模型叫多元线性回归模型。

将提取的特征导入到IBM SPSS Statistics 20中，选择线性回归模型，选取因变量与相应的自变量，得出了如表2的结果：

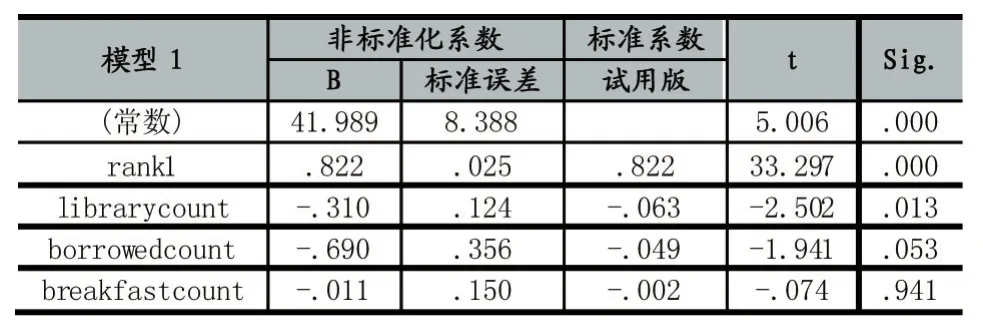
表2 线性回归参数表a

a.因变量：rank2

在非标准化系数下，就计算得到了需要的一组参数。即表明了预测模型对应的公式为：

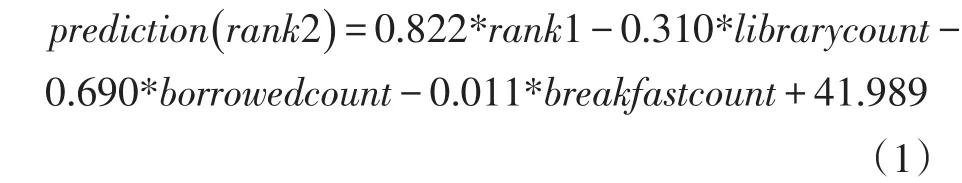
从这组系数可以看出，上学期的成绩排名（rank1）对这个学期（rank2）的影响最大，这个也符合人类的经验。而进图书馆的次数、借阅书籍的次数与吃早餐的次数这些对成绩提高有帮助的因素都会导致相对排名的减小，即相对排名变小。标准化系数可以用来反映变量间相对重要性，但是不能反映在真实情况下对结果的具体影响，因此只是用来分析变量的重要性。

t值是t检验的结果，它的绝对值越大表明了该变量对结果的影响越显著。例如，在上图中可以看出上一学期的成绩对应的t值最大是33.297，那么该变量对结果的影响是最显著的。sig也是用来反映变量对结果影响的显著程度的，但是它的数值的含义是假设某个变量对结果是没有影响的概率。因此，sig的越小表示该变量对结果的影响越大。我们默认当sig小于0.05时，它对结果的影响是显著的，从上图中我们可以看出只有早餐的次数是远大于0.05的，其他变量对结果的影响都是比较大的。因此，可以认为得到公式是有效的。

用以上工作所得到的预测公式对数据中第三学期的学生相对排名做出预测。预测出来的结果如表3所示：

可以看到预测的结果不是整数，且范围不在1～538之间，即这些数字只是反映学生相对排名的一些指标，并不能代表学生的相对排名。所以，又依据这个数据从低到高对学生进行排列，则排列之后的顺序就代表了学生的名次，名次从1依次增大到538，这样就得到了最后的结果。

在预测出学生的相对排名之后，要对预测结果进行评定。在本文中是通过衡量预测排名和实际排名的Spearman相关性，结果为[0，1]之间的数据，数值越大表示相关性越大，即排名预测的越准确。假如有n个学生的排名，学生i的实际排名为ri而该学生的预测排名为 pi，那么Spearman的计算方式如下：

利用这个评价指标对处理后的排名预测进行评价，算出结果为0.901。这表明本文中提取的特征和找到的线性回归模型对学生排名预测是有很好效果的，实际排名和预测排名差别不是很大。

3 结语

本文针对学生的一卡通数据，对学生的行为进行分析。利用可视化图形与交互技术发现影响成绩排名的可能因素。再使用SPSS软件，利用多元线性回归模型，结合可视化交互提取的影响成绩变化的变量，对学生成绩进行预测。实验结果表明，可视化交互提取出的特征对成绩排名的预测有很重要的作用。

表3 初步预测结果

参考文献：

[1]张治斌,王艳萍.数据挖掘技术在数字化校园中的应用[J].现代计算机,2006（12）:93-95.

[2]陈建兵.利用校园一卡通数据优化高校贫困生认定系统[D].电子科技大学,2012.

[3]李珊娜.基于校园一卡通平台的数据挖掘应用研究[J].铁路计算机应用,2010,19（6）:55-58.

[4]陈为,张嵩,鲁爱东.数据可视化的基本原理与方法[M].科学出版社,2013.

[5]Chen M,Jaenicke H.An Information-Theoretic Framework for Visualization[J].IEEE Transactions on Visualization&Computer Graphics,2010,16（6）:1206.

[6]Weber M,Alexa M,Müller W.Visualizing Time-Series on Spirals.[C]Information Visualization,2001.INFOVIS 2001.IEEE Symposium on.IEEE,2001:7-13.