银行间同业拆借利率风险测度研究——基于VaR模型

翁建发

(武汉大学，湖北 武汉 430072)

1 引言

我国从上世纪九十年代开始对利率进行市场化改革，2015年人民银行宣布取消对金融机构存款利率的上限管制，这标志着中国已经结束了利率管制时代。在存在利率管制时，利率变动平稳，因而银行会将主要注意力集中在信用风险控制上；当利率完全依赖于市场时，波动性会加大而不利于预测，这带来了更多的利率风险。在越来越多金融风险暴露的背景下，VaR模型逐步发展起来。VaR模型度量了金融机构利率风险在一定置信度和持有期内可能的最大损失值，相比于早期的利率风险测度方法，有更多优势。

本文基于此背景，选取了我国目前市场化程度最高的同业拆借市场作为研究对象，采用 VaR模型进行实证分析来考察同业市场的利率风险值，并讨论了GARCH族模型对于利率波动率测度的适用性。

2 数据与方法

2.1 数据来源

以银行间同业拆借市场利率作为市场化利率的模拟变量，来测度其波动性以及各银行的利率风险日VaR值。由于数据缺失问题，无法获取近几年各金融机构的拆借头寸数据，因而选取2006年1月9日至2009年6月26日同业拆借市场每日加权平均利率中的860个观测值作为样本数据。并选取这期间外资银行和全国性商业银行的拆借净头寸数据，来计算并比较了外资银行和全国性商业银行面临的利率风险日VaR值。

2.2 VaR的计算方法

VaR值等于波动率乘上资产价值再乘上给定置信水平下分位数，其计算思路是对金融资产的收益率分布做假设，比如序列服从正态分布等，再在各种分布假设下求出VaR值。

VaR=Wασ

(1)

金融资产的价值W以及给定分布假设和置信水平的分位数α均不难得到。广义差分自回归条件异方差模型是目前用来求σ值最普遍的方法，其基本原理、计算过程等将在下一节详细阐述。

3 模型介绍

通过对样本时间序列进行正态性、平稳性、自相关和条件异方差检验，可以得出该序列存在着自相关和异方差的特点。为了消除线性影响，考虑建立一个AR计量模型。根据AIC来确定AR(P)中P的数值，当P=1时，得到的AIC值为所有情况里的最小值。因此确定滞后阶数为1，均值方程为：

chibort=μt+φ1·chibort-1+εt

(2)

确定均值方程后，对残差项进行ARCH效应检验，结果显示残差项有明显的ARCH效应，因此可以用GARCH(p,q)族模型对波动率进行测算，其中，p和q表示滞后阶数。根据赤池信息准则，本文采用GARCH(1,1)族模型来估计利率波动率。

(1)GARCH(1，1)模型：

(3)

(2)TARCH(1，1)模型：

(4)

其中，ω为常数项，ω﹥0；εt﹤0时，dt=1，其他情况则为0；α指利好因子的系数，α与γ的和指利坏因子的系数，若拟合结果中γ显著不等于零，说明有杠杆效应。

(3)EGARCH(1，1)模型：

GARCH模型中，条件异方差的动态性受到了各变量系数非负的约束限制，而EGARCH模型则解决了这一问题。EGARCH(1，1)模型的表达式为：

(5)

一般假设GARCH族模型的残差服从正态分布，但大量实证表明，时间序列数据分布有尖峰厚尾、波动性集群等特点。故在此基础上，学者们也将残差假定为t分布或是GED分布。本文将讨论残差项服从正态分布、t分布、GED分布假设，来计算利率序列的波动率。

4 实证结果

根据GARCH、TARCH、EGARCH模型分布在正态分布、t分布、GED分布下的数据得到的结果，可以得出九种情形下的AIC和LL值。同时，也可以根据P值来判断均值方程和GARCH族模型各项系数是否显著。

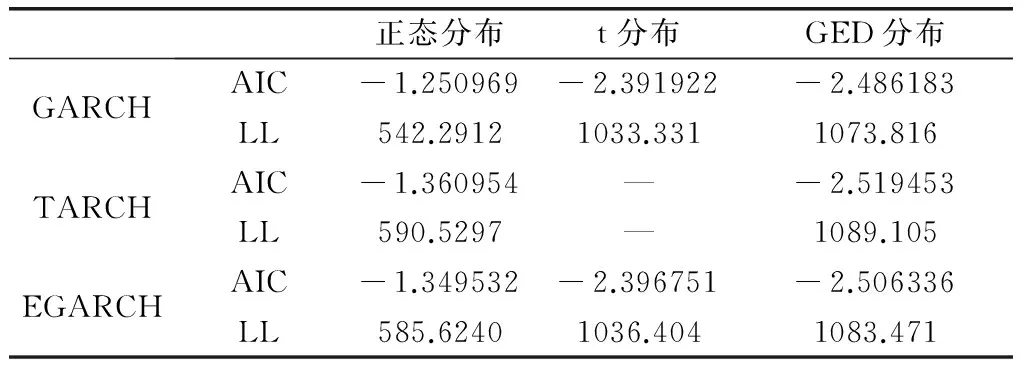
表1 GARCH族模型三种分布下模型的AIC、LL值

根据表1可知，基于GED分布假设的TARCH(1，1)模型的AIC值为-2.519453，为以上所有不同分布下模型中最小值；而LL值为1089.105，为所有情况下最大值。因此，用GED分布假设下TARCH(1，1)模型来估计银行间同业拆借利率序列的波动率效果最好。

在基于GED分布假设的AR(1)-TARCH(1，1)模型估计下，同业拆借利率波动率的均值为0.216198，标准差为1.552988，说明波动并不是十分剧烈。95%置信度下，当自由度等于0.464406，GED分布的分位数等于1.33302。则外资银行的日VaR值为7.454147亿元，全国性商业银行的日VaR值为-21.11718亿元。全国性商业银行的VaR均值绝对值及标准差均大于外资银行，说明前者的利率风险大于后者。

另外，总体来看，假设银行间同业拆借利率序列服从GED分布的假设拥有最好的拟合效果，t分布假设次之，正态分布假设最不符合实际情况。TARCH模型相较于另外两个模型也有更好的拟合结果，EGARCH模型次之，GARCH模型效果最差。

5 结论

本文选用我国银行间同业拆借利率作为为利率变化的代表，选择VaR模型作为测度方式，来测算国内商业银行所面对的每日利率风险值，并选取了基于三种不同分布假设下的GARCH族模型来估计波动率。主要结论如下：

(1)在测度全国同业拆借市场利率的波动率时，基于GED分布的TARCH模型得到的效果最优，基于正态分布的GARCH模型得到的效果最差。

(2)t分布假设下计算的同业拆借利率的日VaR值远高于正态分布和GED分布假设下的VaR值，因此认为，在t分布假设条件下的GARCH族模型存在着高估利率风险的可能性。

(3)GED分布假设下，回归结果的AIC值明显小于正态分布或t分布假设下的值，其LL值也明显更大，说明GED分布假设更符合同业拆借市场利率均值方程的残差项的实际分布。

(4)拟合效果最好的模型得出的结果显示，同业拆借市场利率的日VaR值很大，说明银行在利率市场化背景下利率的风险暴露较大。另外，外资银行和全国性商业银行之间的VaR值差异较大，一方面是由于后者在拆借市场的拆借头寸会高于前者，因而持有的利率敏感性头寸较大；另一方面也是因为国内银行在利率风险监管的观念和方法上都落后于前者。因此，国内商业银行在市场风险管理中加强对利率风险管理是非常有必要的。

[1] 李成,马国校.VaR模型在我国银行同业拆借市场中的应用研究[J].金融研究,2007,(05):62-77.

[2] 王美今,王华.基于GARCH-t的上海股票市场险值分析[J].数量经济技术经济研究,2002，(03):106-109.

[3] 崔树贤.基于VaR测度我国商业银行利率风险的实证研究[J].金融经济,2008,(12):107-108.

[4] 郭奔宇.商业银行利率风险识别实证研究[J].金融研究,2005,(11):62-73.

[5] 李志辉,刘胜会.我国商业银行利率风险的度量研究——以同业拆借市场为例[J].南开经济研究,2006,(03):27-41.

[6] 戴国强,徐龙炳,陆蓉.VaR方法对我国金融风险管理的借鉴及应用[J].金融研究,2000，(07):45-51.

[7] 叶青.基于GARCH和半参数法的VaR模型及其在中国股市风险分析中的应用[J].统计研究,2000，(12):25-29.