CONTINUOUS FINITE ELEMENT METHODS FOR REISSNER-MINDLIN PLATE PROBLEM∗
Huoyuan DUAN(段火元)
School of Mathematics and Statistics,Collaborative Innovation Centre of Mathematics,Computational Science Hubei Key Laboratory,Wuhan University,Wuhan 430072,China
E-mail:hyduan.math@whu.edu.cn
Junhua MA(马俊华)
School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China
E-mail:2015202010036@whu.edu.cn
1 Introduction
The Reissner-Mindlin plate model describes the deformation of a plate with thick to thin thickness,which is subject to a transverse load in terms of transverse displacement of the midplane and rotation of fibers normal to the midplane.In mixed methods,the shear stress is also taken as an independent variable,which plays a bridge role in the finite element analysis of the Reissner-Mindlin plate problem.
As we know,it is important how to avoid shear locking phenomenon and boundary-layer effects in designing finite element methods for solving the Reissner-Mindlin plate problem;see[1,2].Mathematically,it amounts to how to establish convergence independent of the thickness of the plate.This independence strongly relies on the uniform smoothness of the shear stress with respect to the plate-thickness.Therefore,how to approximate the shear stress is critical.
There have been substantial interest in mixed finite element methods or finite element displacement methods,and many articles were available in the literature.Among others,Hu,Ming,and Shi studied several important and useful quadrilateral nonconforming elements;see[3–15].Hybrid elements of practical interest are studied by Xie et al;see[16–21].Some stabilized nonconforming elements are analyzed by Duan;see[22–26].
With certain projection operators,the shear stress can be well-approximated,such as H(curl;Ω)local interpolation,H(div;Ω)(or(H1(Ω))2)global L2projection,(L2(Ω))2local L2projection,etc;see[22,23].Some times,if necessary,the Galerkin variational formulation may be modified,as well as the plate-thickness,such as discontinuous Galerkin method,first-order least-squares method,etc;see[27–30]and references therein.These modifications are generally devoted to the stability of the transverse displacement and the convergence of the shear stress.Moreover,using unstandard finite elements for the shear stress can also yield locking-free(even boundary-layer-effects-free)approximating solutions;for example,see[31],etc.Due to locking phenomenon,to develop efficient fast solvers are important;for example,see[32],etc.
In this article,we propose two new finite element methods to solve the Reissner-Mindlin plate problem.Different from the above literature,we employ continuous elements for transverse displacement and rotation,while shear stress is still element-locally computed.In these methods,the approximating spaces and the norms for the shear stress are important to derive optimal error bounds uniformly in the plate-thickness,in particular for the case of quadrilaterals.
In the first method,the transverse displacement is approximated by conforming(bi)linear macro-elements,and the rotation by conforming(bi)linear elements enriched by local bubble functions.Moreover,the Galerkin formulation is augmented to enhance the stability of the transverse displacement and a local L2projection operator is introduced,because of the gradient of the space for this variable being not a subspace of that for the shear stress.
For triangles,we choose the space of discontinuous piecewise constant polynomials for the shear stress,and for quadrilaterals we choose the same space but carrying a local given function.Thus,transforming this method into a mixed form,we show that the method is uniformly stable and uniformly optimally convergent.
In the second method,the transversedisplacement is approximatedby conforming(bi)quadratic elements,and the rotation by conforming(bi)linear elements.Moreover,the plate-thickness is locally modified.Not any reduction operator is needed,and what choices for the approximating space for the shear stress is unnecessary to consider in practical computations.
For triangles,we choose the space of discontinuous piecewise linear elements for the shear stress,and for quadrilaterals we choose the space which may be viewed as certain variant of thefirst-order Raviart-Thomas rectangular element also carrying the same local function as in thefirst method.Thus,transforming this method into a mixed form,we also obtain optimal error bounds,uniform in the plate-thickness.
When analyzing these two methods,the key point for the first method is that we can control the jumps of the normal components of the shear stress across interelement boundaries;while that for the second method is that the transverse displacement may be split as two parts which have different regularities with respect to the plate-thickness and this split make it unnecessary to control the normal traces of the shear stress,since two parts can be independently estimated in different manners.It should be noted that this split-trick can be employed only in the case of using at least(bi)quadratic elements for the transverse displacement,if not any reduction operator is introduced.
In addition,needless to say,the well-known continuous Helmholtz decomposition for the shear stress is a very useful tool in constructing a reasonable interpolant for this variable.This reasonability means that the uniform regularity of this variable with respect to the platethickness should not be violated.To a great degree,the choices of the finite element spaces for this variable is at the mercy of this decomposition,at least in the case of quadrilaterals.
An outline of article is arranged as follows:In Section 2,a preliminaries about the Reissner-Mindlin plate model is given.In Section 3,two finite element methods are proposed for triangles and quadrilaterals.In Section 4,the first method is analyzed to obtain stability and convergence.In Section 5,error bounds are derived for the second method.A numerical test is performed in the last section.
2 The Reissner-Mindlin Plate Model
Let Ω be the midplane occupied by the plate with thickness t> 0.The Reissner-Mindlin plate model under a clamped boundary condition is to find the rotation θ =(θ1,θ2)∈ ((Ω))2and the transverse displacement w ∈(Ω)such that(see[2])
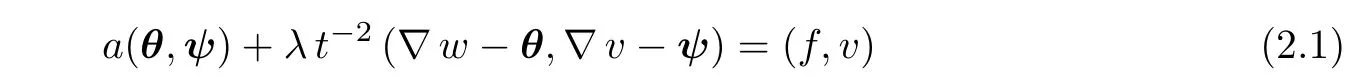

where E(θ)is the linear strain tensor(the symmetric part of the gradient of θ).
Introducing the shear stress

as an independent variable,problem(2.1)can be formulated in a mixed form:Find(θ,w,γ)∈such that

From(2.4),if the exact solution(θ,w,γ)is sufficiently smooth,then we can obtain the partial differential equations as follows:
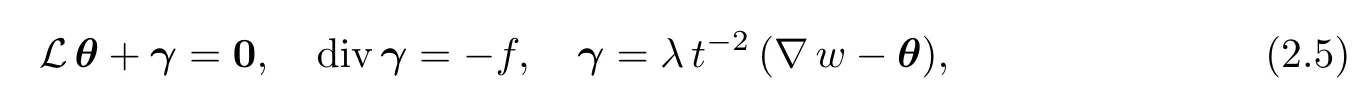
where L is the partial differential operator associated with a(·,·).
In addition,as t → 0,from[33],the solution(θ,w,γ)of(2.4)weakly converges towhere(θ0,w0,γ0)is the solution to the Kirchhoff-Love thin plate problem as follows:

where

which is provided with norm
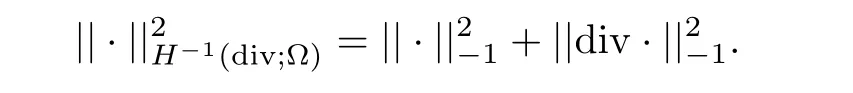
The following two propositions can be found in[2].
Proposition 2.1a(·,·)is a symmetric continuous bilinear form onand is(H10(Ω))2-elliptic,that is,

Above and below,the letter C denotes the generic positive constant which may take different values at different occurrences,but always independent of the mesh-parameter and the platethickness.In addition,·k,with k ∈ ℜ,denotes the standard Sobolev norm for Hk(Ω).
Proposition 2.2For any γ ∈ (L2(Ω))2,there holds the following Helmholtz decomposition:

Proposition 2.3([28]) Let Ω be a convex polygonal or smooth bounded domain in the plane.For any t,0< t< C,χ ∈ (L2(Ω))2,and f ∈ L2(Ω),there exists a unique solutionsuch that

and we have

with γ = ∇u+curlp being the Helmholtz decomposition.
If f=0,then w ∈ H3(Ω),and we have

If χ=0,and let w be split into two parts as follows:

where w0is the solution to(2.6)and wris the residual term,we have

Proposition 2.4(2.4)and(2.10)can be also respectively written as the augmented and condensed forms as follows:

where

ProofNoting that

we add the following term

to(2.4)and(2.10),respectively;after a minor arrangement,we get(2.15)–(2.18).
Remark 2.5In this article,Method(I)will be based on this augmentation form(2.15)-(2.18).Generally,this augmentation may be used to enhance the stability of the transverse displacement when the approximating space for the shear stress does not include the gradient of the approximating space for the transverse displacement.
Method(II)will be based on(2.1).
Throughout this article,we always assume that λ =1 and 0 < t< 1 and Ω is a convex polygonal or smoothly bounded domain.
3 The Finite Element Method
Let Thbe the standard regular triangulation(see[34])of Ω into triangles or quadrilaterals,with the mesh-parameter h=maxK∈ThhKand hKthe diameter of K.
Denote byˆK the reference element,and let FK:→K be the usual invertible mapping.With K andˆK,we associate four vertices(xi,yi)and(ξi,ηi),(1≤i≤4),respectively.Corresponding to K,we introduce local base functions λi(barycenter coordinates)for triangles,or Ni(ξ,η)=(1+ ξiξ)(1+ ηiη)/4 for quadrilaterals.In addition,Pm(K)is the space of polynomials of order in two variables not greater than m,and Qm(K)◦FKis the space of polynomials of order in each variable not greater than m.
Introducing

For transverse displacement,we define Whand Zh,respectively,by

where K is divided into four equal parts by joining the midpoints of the sides,

For rotation,we define Θhand Σh,respectively,by
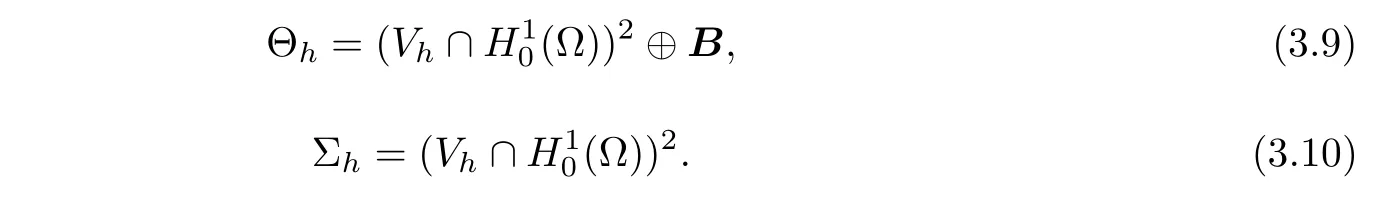
For the shear stress,we define Γhand Dh,respectively,by

Note that the finite element space Dhfor the shear stress in Method(II)is only for theoretical analysis.If necessary,the shear stress is computed directly from the transverse displacement and rotation(see(3.18)below).
Let Mhbe composed of macro-elements,where each macro-element M∈Mhconsists of two elements in Thsharing a common edge.Clearly,the base functions of What mid-points are bubbles on corresponding macro-elements.In addition,the number of these base functions is equal to the number of macro-elements in Mh,or the number of edges in S0,where S0is the set of all interior element-edges in Th.Let ϕMbe the base function on M corresponding to the mid-point on the common edge e⊂M,we introduce

We also introduce a standard L2-projection operator as follows:

We now state the two finite element problems as follows:
Method(I)Find(θh,wh)∈ Θh×Whsuch that
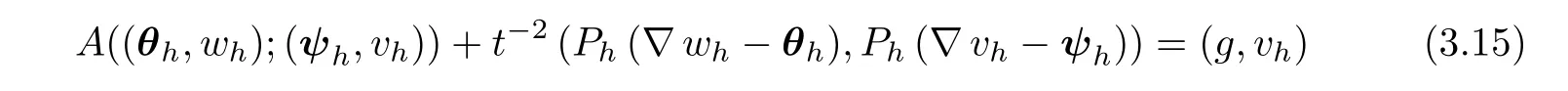
holds for all(ψh,vh)∈ Θh×Wh,while γh∈ Γhis given by

where A(·;·)is defined as in(2.17),and g is defined as in(2.18).
Method(II)Find(θh,wh)∈ Σh×Zhsuch that

holds for all(ψh,vh)∈ Σh×Zh,while γh∈ Dhis given by

Remark 3.1Note that in Method(I),we use the augmented bilinear form A(·;·)defined by(2.17),while in Method(II),we use the primal bilinear form a(·;·)defined by(2.2).
Degrees of freedom for these methods with triangles and quadrilaterals are depicted in Figures 1–6,where•denotes the degree of freedom in the usual sense,while◇ and◁denote the degrees of freedom related withandrespectively.

Figure 1 Method(I)for triangles

Figure 2 Method(I)for quadrilaterals

Figure 3 Method(II)for triangles

Figure 4 Method(II)for quadrilaterals

Figure 5 γ—P0and P+0for triangles and quadrilaterals in Method(I)

Figure 6 γ—P1and Q+1for triangles and quadrilaterals in Method(II)
Remark 3.2The special functionmakes it easy to construct a reasonable interpolant to the shear stress in the case of quadrilaterals;see Lemma 4.5 in Section 4.
Remark 3.3As far as Method(II)is concerned,the finite element spaces for the shear stress are only used for theoretical analysis,and in practical computations,they are not needed.
4 Error Analysis for Method(I)
Method(I)can be stated in the form:Find(θh,wh,γh)∈ Θh×Wh×Γh,such that

Let nebe the exterior unit normal vector to e,and let[s·ne]be the jump along e and he=|e|,we define
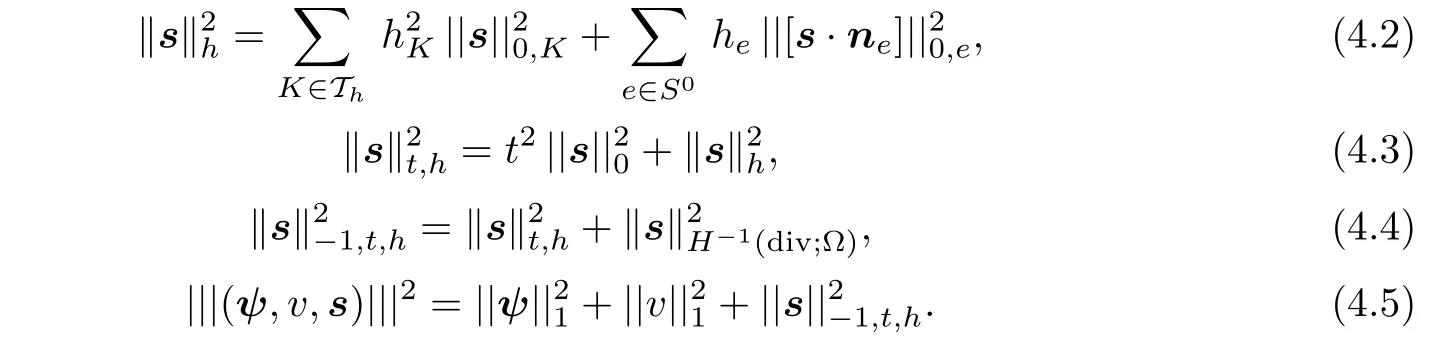
Lemma 4.1There holds

ProofThe proof is divided into two steps.
Step 1Because of s|K∈Y0(K),takingand choosing

we have

Step 2Choosing

which is the subspace of all the base functions in What mid-points,see(3.13).
Because of s·n being a constant on e,we choose

and by divs|K=0,we have

Combining(4.8),(4.9)and(4.12),(4.13),we have(4.6).
Remark 4.2(4.6)may be viewed as a discret version of(2.8).In addition,the meshdependent norm·his to some degree an approximate form of the minus norm·H−1(div;Ω),noting that divs|K=0,∀K ∈ Th.As it is known in[2,33],when the Reissner-Mindlin plate degenerates into the Kirchhoff-Love thin plate with t→ 0,the right norm for the shear stress is only·H−1(div;Ω).Therefore,the introduction of·his reasonable at least from the mathematical point of view.
Theorem 4.3There holds

on Θh×Wh×Γh.
ProofWe first see that
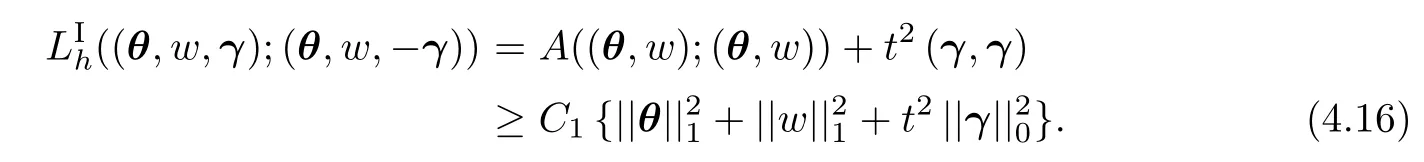
Secondly,from Lemma 4.1,we see that there exists(ψh,vh)∈Θh×Wh,such that
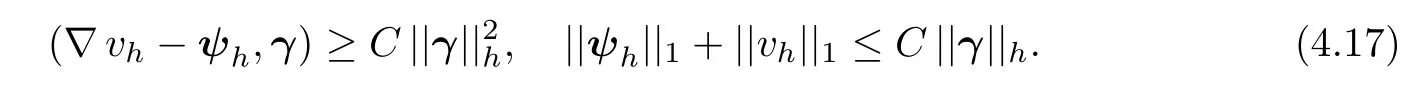
Then,we get

Thirdly,(2.8)in Proposition 2.1 implies that there existssuch that

By the Clément-interpolation([34–36]),we can findsuch that

Then,by divγ|K=0,we have

Finally,putting

where

and combining(4.16),(4.18),and(4.22),we obtain

It follows from(4.25)and(4.26)that(4.14)holds.
In what follows,we show(4.15).In fact,(4.15)results from(4.27)-(4.31)as follows:
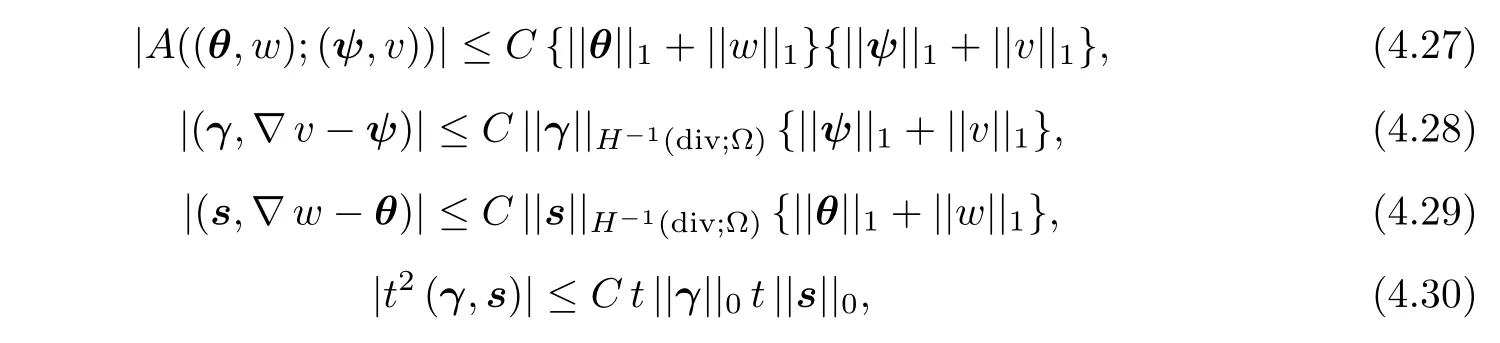

Lemma 4.4There holds

Proof(4.32)is obviously true for triangles.We next consider quadrilaterals.This was proved in[37].We nevertheless reproduce it here for completeness.
For all v∈Vh,letwhere vi,(1≤i≤4),are nodal values of v,Ni=(1+ ξiξ)(1+ ηiη)/4,(1 ≤ i ≤ 4),are local base functions,with vertices(ξi,ηi) ∈{(1,1),(−1,1),(−1,−1),(1,−1)}.
To show(4.32),we only need to show that

In fact,as

we have

By virtue of the shape-regularity of the triangulation Th,we know that

is a non-singular matrix,and by solving(4.35),we have

with(ai,bi,di)being some constants.Thus,the proof is finished.
Lemma 4.5Define an interpolant∈ Γhto γ=∇u+curlp withand p∈ H1(Ω)/ℜ in the following way:


ProofBy Lemma 4.4,we know that∈Γh.
Note that
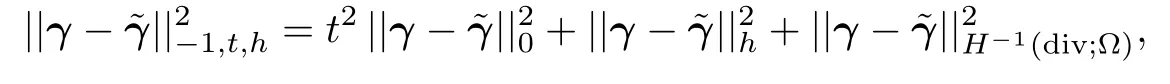
we have

It follows that(4.39)holds.
Theorem 4.6Let(θ,w,γ)and(θh,wh,γh)be the exact solution and the finite element solution,respectively.Then,
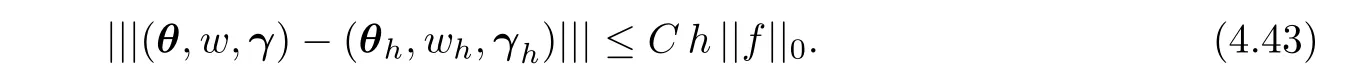
ProofForfrom Theorem 4.3,we have

Theorem 4.7Under the same hypotheses as in Theorem 4.6,there holds

ProofWe consider the dual problem:Findsuch that

whose solution(φ,z,q)satisfies

where

(4.45)can be reformulated in the form:Find(φ,z,q)such that

In(4.45),taking v=w−wh,ψ=θ−θh,and s=γ−γh,we have
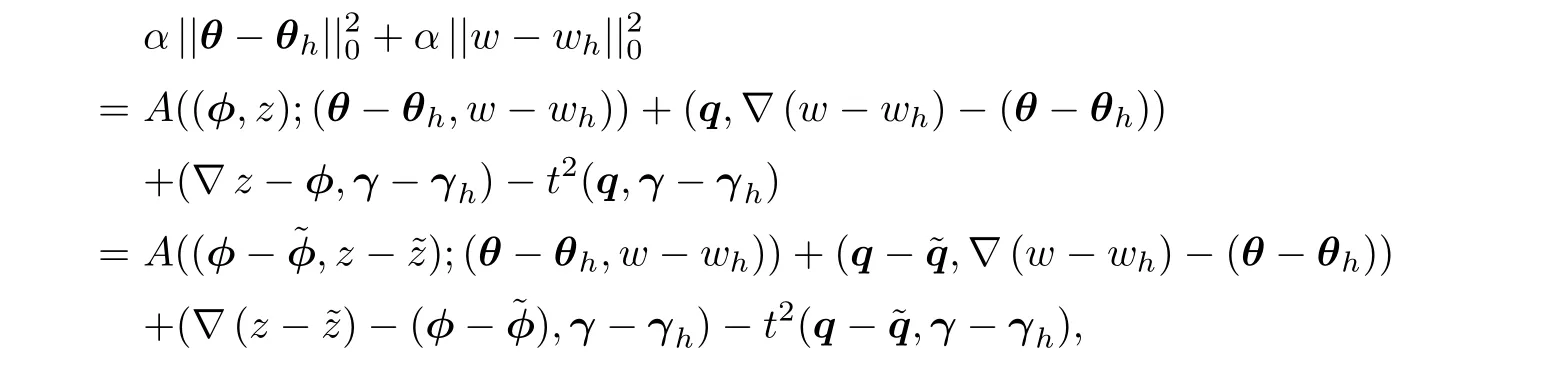
where

It follows that(4.44)holds.
Remark 4.8In Method(I),if we add a stabilization term

to(4.1),then we can use conforming(bi)linear elements for both transverse displacement and rotation,because it is unnecessary to use Whto control the normal traces of the shear stress.However,in this case,(4.1)cannot be reduced into(3.15),because of the jumps term(4.53).
5 Error Analysis for Method(II)
Method(II)can be stated as follows:Find(θh,wh,γh)∈ Σh×Zh×Dhsuch that


Define

Remark 5.1In Method(II),the jumps across interelement boundaries for the normal components of the shear stress cannot be controlled from Wh,unless Whis(bi)cubic elements.
Lemma 5.2There holds

Proof(5.6)is obviously true for triangles.We next consider quadrilaterals.
As

from Lemma 4.4,we know that

which completes the proof.□
Theorem 5.3There holds

for all(θ,w,q)∈ Σh×Zh×Dh.
ProofWe first see that

Next,by Lemma 5.2,choosing∇w∈Dh,we obtain
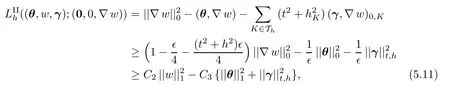
with
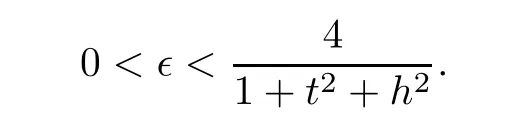
In addition,using Clément-interpolation,we can find a χh∈ Σhsuch that

with

Finally,choosing
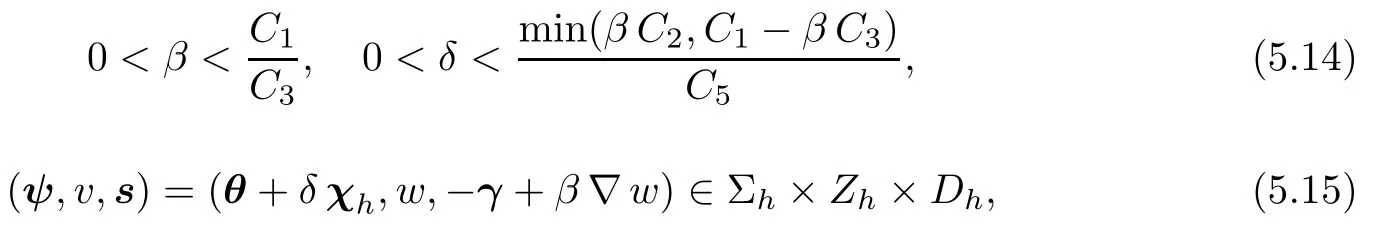
from(5.10),(5.11),and(5.12),we have

Moreover,it can be easily seen that

Hence,(5.9)follows from(5.16)and(5.17).
Theorem 5.4Let(θ,w,γ)and(θh,wh,γh)be the exact and finite element solutions,respectively.Then,

ProofOwing to(see Proposition 2.3)

we define

as the interpolant to w.Also,as usual,letbe the Lagrangian interpolant to θ,anddefined in the manner similar to Lemma 4.5,is the interpolant toand Phis a standard L2projection operator onto Dh.
From Theorem 5.3,we have

where

Therefore,we have

Noting that

from(5.30)and(5.27),we have

which completes the proof.
Theorem 5.5Under the same hypotheses as in Theorem 5.4,there holds

ProofWe consider the dual problem:Find(φ,z,q)∈ (H10(Ω))2×H10(Ω)×(L2(Ω))2such that

whose solution(φ,z,q)satisfies
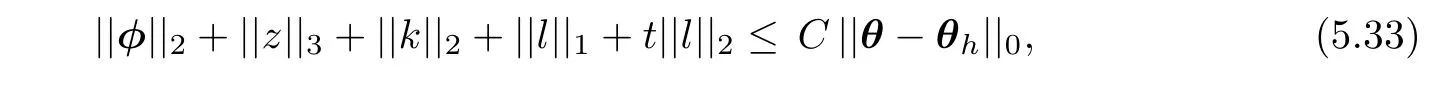
where

In(5.32),taking v=w−wh,ψ=θ−θh,and s=γ−γh,we have
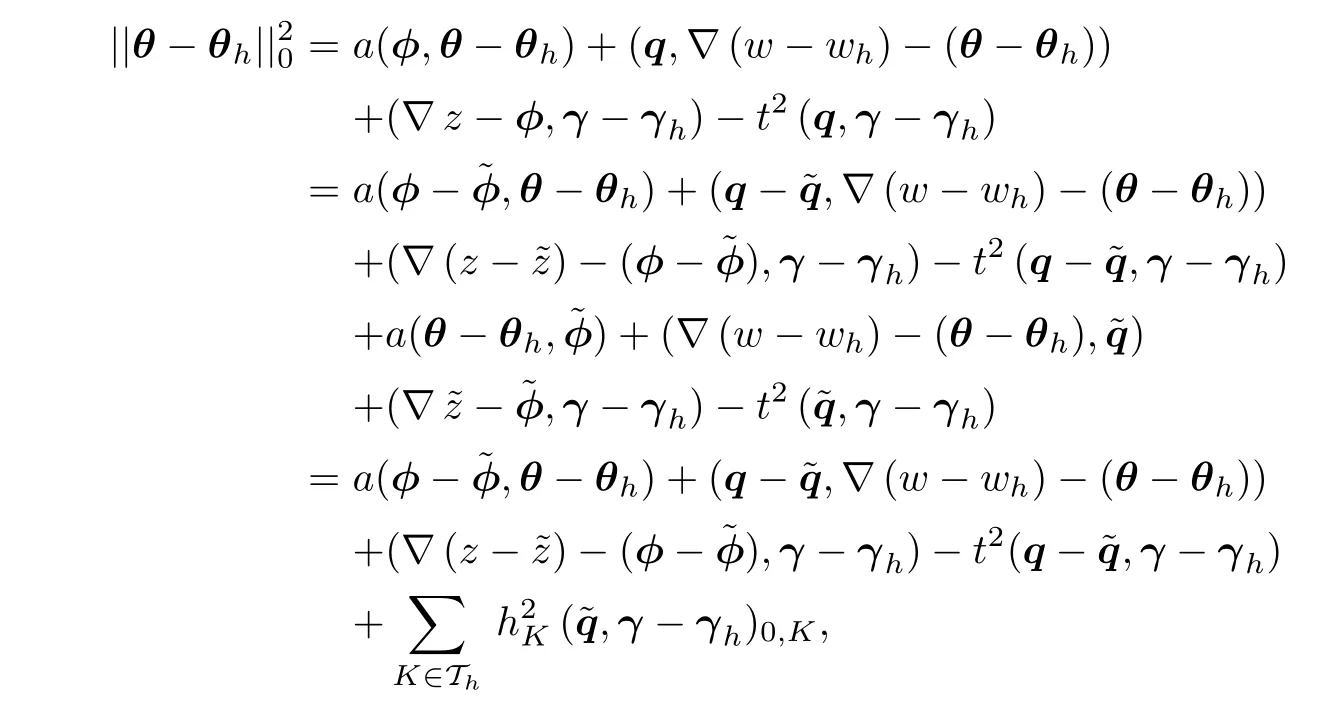
where

Theorem 5.6Under the same hypotheses as in Theorem 5.4,and assuming that w∈H3(Ω),we have

ProofIn view of

we have

On the other hand,by∇Zh⊂Dh,taking s=∇vhin(5.1),we have

Subtracting(5.43)from(5.42),for all vh∈Zh,we have

from which we have

Choosing vh=−wh,we get

where

Therefore,from(5.47)and(5.48),we can conclude that(5.40)holds,with the standard interpolation estimation for w−˜w.
6 A Numerical Test
In this section,we give a numerical test to perform Method(II)to con firm the theoretical results obtained in the previous section.
In Method(II),we use the bilinear element for rotation and the biquadratic element for transverse displacement.We thus consider the following finite element scheme:

where

Assume that Ω=[0,1]2.Choosing

such that we have the exact solutions as follows:
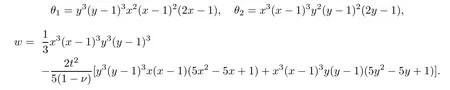
We partition Ω into squares,with h=1/8,1/16,1/32,1/64.In addition,set

and t=0.1,0.01,0.001,0.0001,0.00001.
We compute the H1and L2-relative errors for w − whand L2-relative errors for θ − θh,listing in Tables 1–4.

Table 1h=1/8

Table 2 h=1/16
From Tables 1–4,for any two consecutive sets of error data with respect to the mesh sizes h1 and h2,we can compute the rate of conv:=ln(‖e1‖/‖e2‖)/ln(h1/h2)which is about two.We also see that the errors are independent of the plate-thickness t.This con firms our theoretical results,that is,

where C is independent of t.
[1]Arnold D N,Falk R S.The boundary layer for the Reissner-Mindlin plate model.SIAM J Math Anal,1990,21:281–317
[2]Brezzi F,Fortin M.Mixed and Hybrid Finite Element Methods.New-York:Springer-Verlag,1991
[3]Hu J,Shi Z C.Analysis of nonconforming rotated Q1 element for the Reissner-Mindlin plate problem//Industrial and Applied Mathematics in China,Ser Contemp Appl Math CAM,10.Beijing:Higher Ed Press,2009:101–111
[4]Hu J,Shi Z C.Analysis for quadrilateral MITC elements for the Reissner-Mindlin plate problem.Math Comp,2009,78:673–711
[5]Hu J,Shi Z C.Two lower order nonconforming quadrilateral elements for the Reissner-Mindlin plate.Sci China Ser A,2008,51:2097–2114
[6]Hu J,Shi Z C.Error analysis of quadrilateral Wilson element for Reissner-Mindlin plate.Comput Methods Appl Mech Engrg,2008,197:464–475
[7]Hu J,Shi Z C.Two lower order nonconforming rectangular elements for the Reissner-Mindlin plate.Math Comp,2007,76:1771–1786
[8]Hu J,Shi Z C.On the convergence of Weissman-Taylor element for Reissner-Mindlin plate.Int J Numer Anal Model,2004,1:65–73
[9]Hu J,Ming P B,Shi Z C.Nonconforming quadrilateral rotated Q1 element for Reissner-Mindlin plate.J Comput Math,2003,21:25–32
[10]Ming P B,Shi Z C.Optimal L2 error bounds for MITC3 type element.Numer Math,2002,91:77–91
[11]Ming P B,Shi Z C.Convergence analysis for quadrilateral rotated Q1 elements//Kananaskis A B.Scientific Computing and Applications,Adv Comput Theory Pract,7.New-York:Nova Sci Publ,2001:115–124
[12]Ming P B,Shi Z C.Nonconforming rotated Q1 element for Reissner-Mindlin plate.Math Models Methods Appl Sci,2001,11:1311–1342
[13]Ming P B,Shi Z C.Some low order quadrilateral Reissner-Mindlin plate elements//Recent Advances in Scientific Computing and Partial Differential Equations(Hong Kong,2002),Contemp Math,330.Providence,RI:Amer Math Soc,2003:155–168
[14]Ming P B,Shi Z C.Two nonconforming quadrilateral elements for the Reissner-Mindlin plate.Math Models Methods Appl Sci,2005,15:1503–1517
[15]Ming P B,Shi Z C.Analysis of some low order quadrilateral Reissner-Mindlin plate elements.Math Comp,2006,75:1043–1065
[16]Guo Y H,Xie X P.Uniform analysis of a stabilized hybrid finite element method for Reissner-Mindlin plates.Sci China Math,2013,56:1727–1742
[17]Carstensen C,Xie X P,Yu G Z,Zhou T X.A priori and a posteriori analysis for a locking-free low order quadrilateral hybrid finite element for Reissner-Mindlin plates.Comput Methods Appl Mech Engrg,2001,200:1161–1175
[18]Yu G Z,Xie X P,Zhang X.Parameter extension for combined hybrid finite element methods and application to plate bending problems.Appl Math Comput,2010,216:3265–3274
[19]Guo G H,Xie X P.On choices of stress modes for lower order quadrilateral Reissner-Mindlin plate elements.Numer Math J Chin Univ(Engl Ser),2006,15:120–126
[20]Xie X P.From energy improvement to accuracy enhancement:improvement of plate bending elements by the combined hybrid method.J Comput Math,2004,22:581–592
[21]Zhou T X,Xie X P.A combined hybrid finite element method for plate bending problems.J Comput Math,2003,21:347–356
[22]Duan H Y,Liang G P.A locking-free Reissner-Mindlin quadrilateral element.Math Comp,2004,73:1655–1671
[23]Duan H Y.A finite element method for plate problem.Math Comp,2014,83:701–733
[24]Duan H Y,Liang G P.Analysis of some stabilized low-order mixed finite element methods for Reissner-Mindlin plates.Comput Methods Appl Mech Engrg,2001,191:157–179
[25]Duan H Y,Liang G P.An improved Reissner-Mindlin triangular element.Comput Methods Appl Mech Engrg,2002,191:2223–2234
[26]Duan H Y,Liang G P.Mixed and nonconforming finite element approximations of Reissner-Mindlin plates.Comput Methods Appl Mech Engrg,2003,192:5265–5281
[27]Arnold D N,Brezzi F,Falk R S,Marini L D.Locking-Free Reissner-Mindlin elements without reduced integration.Comput Methods Appl Mech Engrg,2007,196:3660–3671
[28]Arnold D N,Falk R S.A uniformly accurate finite element method for the Reissner-Mindlin plate.SIAM J Numer Anal,1989,26:1276–1290
[29]Behrens E M,Guzmán J.A new family of mixed methods for the Reissner-Mindlin plate model based on a system of first-order equations.J Sci Comput,2011,49:137–166
[30]Bosing P R,Madureira A L,Mozolevski I.A new interior penalty discontinuous Galerkin method for the Reissner-Mindlin model.Math Models Methods Appl Sci,2010,20:1343–1361
[31]Zhou T X.The partial projection method in the finite element discretization of the Reissner-Mindlin plate.J Comput Math,1995,13:172–191
[32]Schöberl J,Stenberg R.Multigrid methods for a stabilized Reissner-Mindlin plate formulation.SIAM J Numer Anal,2009,47:2735–2751
[33]Destuynder P.Mathematical Analysis of Thin Shell Problems.Paris:Masson,1991
[34]Ciarlet P G.The Finite Element Method for Elliptic Problems.Amsterdam:North-Holland,1978
[35]Clément P.Approximation by finite elements using local regularization.RAIRO Anal Numer,1975,8:77–83
[36]Girault V,Raviart P A.Finite Element Methods for Navier-Stokes Equations,Theory and Algorithms.Berlin:Springer-Verlag,1986
[37]Duan H Y,Liang G P.Nonconforming elements in least-squares mixed finite element methods.Math Comp,2004,73:1–18
 Acta Mathematica Scientia(English Series)2018年2期
Acta Mathematica Scientia(English Series)2018年2期
- Acta Mathematica Scientia(English Series)的其它文章
- ON A FIXED POINT THEOREM IN 2-BANACH SPACES AND SOME OF ITS APPLICATIONS∗
- MULTIPLICITY AND CONCENTRATION BEHAVIOUR OF POSITIVE SOLUTIONS FOR SCHRÖDINGER-KIRCHHOFF TYPE EQUATIONS INVOLVING THE p-LAPLACIAN IN RN∗
- MULTIPLICITY OF SOLUTIONS OF WEIGHTED(p,q)-LAPLACIAN WITH SMALL SOURCE∗
- QUALITATIVE ANALYSIS OF A STOCHASTIC RATIO-DEPENDENT HOLLING-TANNER SYSTEM∗
- SHARP BOUNDS FOR HARDY OPERATORS ON PRODUCT SPACES∗
- A NOTE ON MALMQUIST-YOSIDA TYPE THEOREM OF HIGHER ORDER ALGEBRAIC DIFFERENTIAL EQUATIONS∗
