SHARP BOUNDS FOR HARDY OPERATORS ON PRODUCT SPACES∗

Mingquan WEI(魏明权)

School of Mathematics and Statistics,Xinyang Normal University,Xinyang 464000,China

E-mail:weimingquan11@mails.ucas.ac.cn

Dunyan YAN(燕敦验)

School of Mathematical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

E-mail:ydunyan@ucas.ac.cn

1 Introduction

Let f be a non-negative integrable function on G.The classical Hardy operator is defined by

for x∈G,where G=(0,+∞).

The following Theorem A,because of Hardy[1],is well-known.

Theorem AIf f is a non-negative measurable function on G and 1＜p＜∞,then

In 1976,Faris[2] first gave a definition of Hardy operator in n-dimensional case.In 1995,Christ and Grafakos[3]gave its equivalent version of n-dimensional Hardy operator

where f is a non-negative measurable function on Rnandis the volume of the unit ball in Rn.The norm of Hnon Lp(Rn),1＜p＜∞,was evaluated in[3]and found to be equal to the one dimensional Hardy operator,that is,

For the case of n-dimensional product spaces,the Hardy operator is defined by

for x=(x1,x2,···,xn)∈ Gn,where Gn=(0,+∞)× ···× (0,+∞)is a product space and f is a non-negative measurable function on Gn.In 1992,Pachpatte[4]investigated the operator defined by(1.4)and obtained the following Theorem B.

Theorem BIf f is a non-negative measurable function on Gnand 1＜p＜∞,then

It is often important to obtain sharp norm estimates for Hardy-type integral inequalities.Readers can refer to[5]to get some earlier development of Hardy operator.There are also many articles dealing with such inequalities such as[6,7,21,22].

As|Hnf|≤Mf and the centered Hardy-Littlewood maximal operator is of weak type(1,1),it is obtained that Hnis also of weak type(1,1).A.Melas[8]found the exact value of the best possible constant C=1.5675208···for the weak-type(1,1)inequality of one-dimensional centered Hardy-Littlewood maximal operator.However,the best constant in the weak type(1,1)inequality for certain centered maximal operators in Rn(n≥2)is still open(see[9]).

In 2011,Fayou Zhao et al[20]got the weak-type(p,p)bound of n-dimensional Hardy operator,which is stated as follows.

Theorem CFor 1≤p≤∞,the following inequality

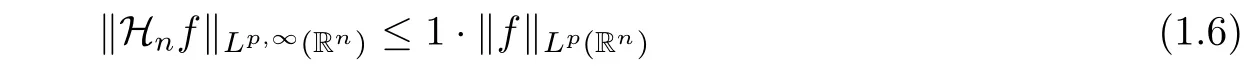
holds.Moreover,

where the bound 1 is best.

Unfortunately,the operator Hnis even not of weak type(1,1)when n≥2(In Section 2,we will give an example).In order to study the general weak(1,1)type inequality for Hn,we shall consider another space instead of L1(Gn).The refined definitions of mixed-norm space will be presented in Section 2.

2 Preliminaries

Before we prove the main results,some useful lemmas and definitions will first be given.

Lemma 2.1The operator Hn,n≥2,defined by(1.4)fails to be of weak type of(1,1).

ProofWe merely consider the case n=2,and the same is true for n≥3.

Let f(t)= χ(0,1](t),where χAis the characteristic function of the set A.Define a binary function on G2as F(x,y)=f(x)f(y)and then F is our desired function.For more details of the proof,readers can refer to[10]by Di Wu.

Lemma 2.2The operator H,defined by(1.1),is of weak type of(p,p)(1≤p≤∞)with the sharp bound 1.

Taking n=1 in Theorem C,it is obtained that Lemma 2.2 is a direct consequence.

In[11],A.Benedek and R.Panzone introduced the space LPwith mixed norm.

Definition 2.3Let(Xi,Si,µi),for 1 ≤ i≤ n,be n given,totally σ- finite measure spaces and P=(p1,p2,···,pn)a given n-tuple with 1 ≤ pi≤ ∞.A function f(x1,x2,···,xn)measurable in the product spacesis said to belong to LP(X)if the number obtained after taking successfully the p1-norm in x1,the p2-norm in x2, ···,the pn-norm in xn,and in that order,is finite.The number so obtained, finite or not,will be denoted by

Obviously,the space LPwith mixed norm is a Banach space.In addition,there are some properties similar to that of the classical Lpspace and readers can refer to[11]for more information.After that,there are numerous articles dealing with the boundedness on the space LPsuch as[12–17].

Now,we take the steps further by transform the Lpnorm to the weak Lpnorm and naturally obtain the weak LPmixed-norm space.

Definition 2.4Let(Xi,Si,µi),for 1 ≤ i≤ n,be n given,totally σ- finite measure spaces and P=(p1,p2,···,pn)a given n-tuple with 1 ≤ pi≤ ∞.A function f(x1,x2,···,xn)measurable in the product spacesis said to belong to the space wLP(X)if the number obtained after taking successfully the weak p1-norm in x1,the weak p2-norm in x2,···,the weak pn-norm in xn,and in that order,is finite.The number so obtained, finite or not,will be denoted by ‖f‖wP,‖f‖w(p1,···,pn),or ‖f‖wp1,···,wpn.

Similarly,we can also give the definition of the weak and strong LPmixed-norm space.

Definition 2.5Let(Xi,Si,µi),for 1 ≤ i≤ n,be n given,totally σ- finite measure spaces and P=(p1,p2,···,pn)a given n-tuple with 1 ≤ pi≤ ∞.The set I satisfies I ⊂ {1,···,n}.A function f(x1,x2,···,xn)measurable in the product spacesis said to belong to the space LPI(X)if the number obtained after subsequently taking successfully the pi-norm for i∈ I while taking the weak pj-norm for j ∈ {1,···,n}I and in natural order is finite.The number so obtained, finite or not,will be denoted by ‖f‖PI.

From the above definitions,we immediately obtain the following results:

Remark 2.6(i)The spaces wLP(X)and LPI(X)are all quasi-normed linear spaces for p≥1.

(ii)The space LPI(X)equals to wLP(X)for the set I=Ø while it is equal to LP(X)for I={1,···,n}.

(iii)For any P≥1,and any f in LP(X),we have

and hence

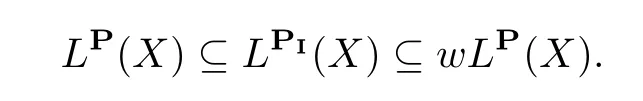
For the mixed-norm space,we have a basic lemmas which plays an important role in the proof of our main theorems.

Lemma 2.7Let(X,S,µ)be defined as in the above definitions,pn≥ ···≥ p1≥ 1,and f ∈ Lpn,···,p1(X).Then,f ∈ Lp1,···,pn(X)and there holds

Obviously,when p1=1 and n=2,Lemma 2.7 becomes the common Minkowski’s inequality(see[18]).So,Lemma 2.7 is a direct generation of the Minkowski’s inequality.For the proof of the lemma,readers can refer to[19].

In the following,we always consider the spaces on Euclidean Spaces.

3 Main Results

Now,we formulate our main theorems.We first give the boundedness of Hardy operator on product spaces from L1(Gn)to wL1,···,1(Gn).

Theorem 3.1The operatorHn,defined by(1.4),is bounded from L1(Gn)to wL1,···,1(Gn),and furthermore,we have

ProofTo make the argument more easily to be understood, first we shall prove the boundedness of case n=2,and then case n≥3 is just a repetition of n=2.

For n=2,the operator H2can be written as

As f∈L1(G2),we have

for all x2∈G.Thus,Lemma 2.2 yields that

Using Fubini’s Theorem,it is not hard for us to obtain

Obviously,

while f∈L1(G2).Then,applying Lemma 2.2 again,we obtain

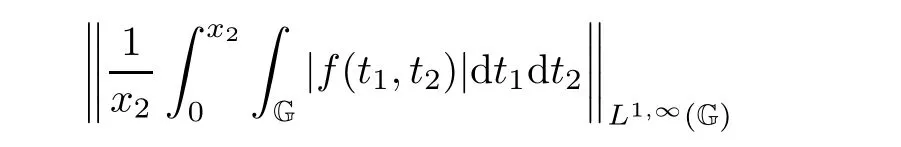
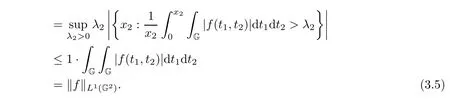
Combining(3.3),(3.4)with(3.5),it yields

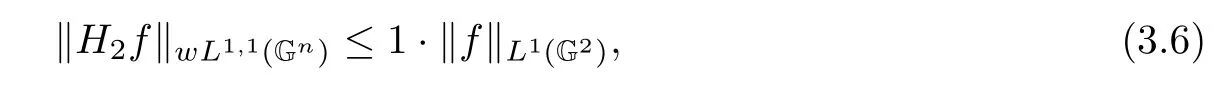
for all f∈L1(G2).

On the other hand,we will show that the constant 1 is the best possible. Denote χr= χ[0,r],r＞ 0.Taking f0(x)= χr(x),x∈ G and choosing F(x1,x2)=f0(x1)f0(x2),we obtain from the definition of H2by(1.4)

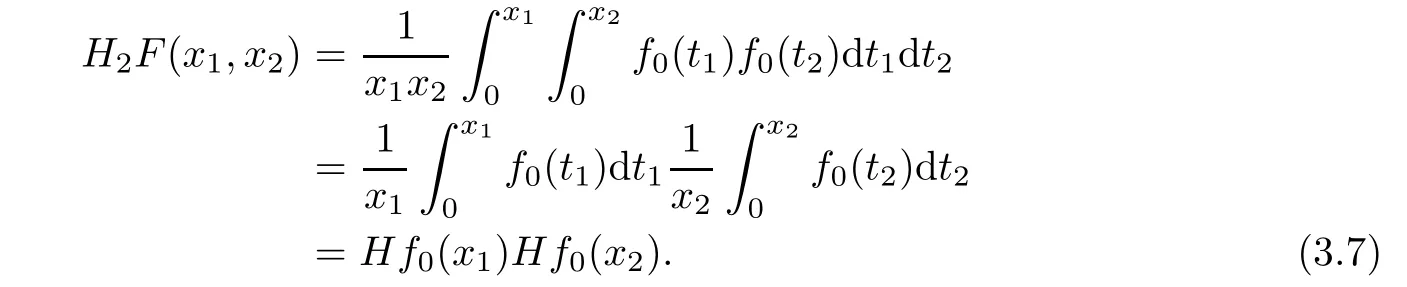
(i)When r＞x1,

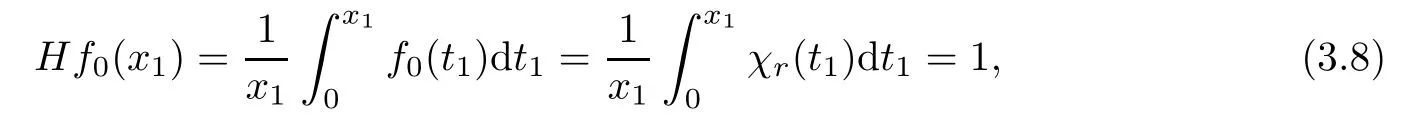
then,

(ii)When r≤x1,

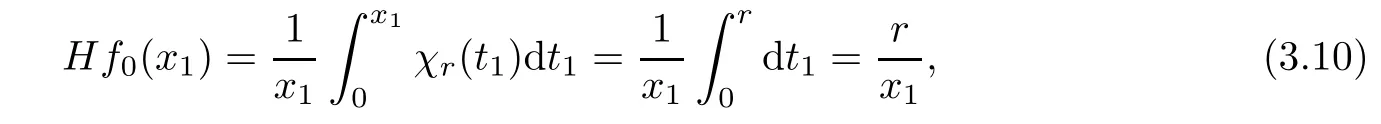
then,

From the above results,we have the following estimate,

Evidently,‖f0‖L1(G)=r.It implies from above that

For 0 ＜ λ2＜ ‖f0‖L1(G),we also divide r into two cases:r ＞ x2and r ≤ x2.A similar computation yields

Combining(3.13)with(3.15),it yields

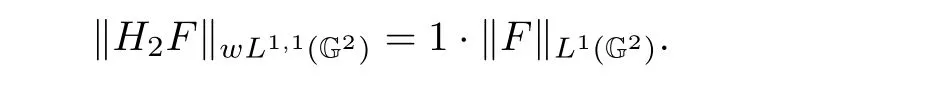
This finishes the proof of Theorem 3.1.

Next,we shall formulate the boundedness from LP(Gn)to wLP(Gn).

Theorem 3.2For 1 ≤ pi≤ ∞,i=1,···,n,the following inequality

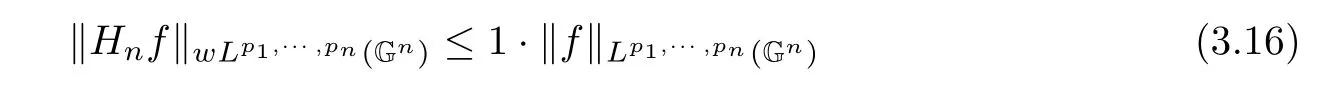
holds.Moreover,

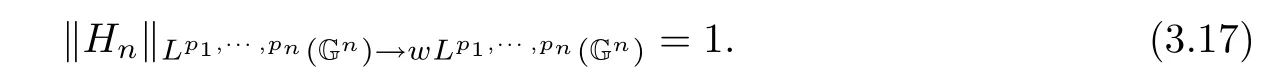
ProofWe merely prove the case n=2.The case n≥3 is just the same as n=2.As there are some similarities between the proof of Theorem 3.1 and the proof of Theorem 3.2,we omit some details.

It is not hard to verify Theorem 3.2 for p1=∞or p2=∞.Indeed,it is just a corollary of Lemma 2.2.So,suppose that 1≤p1,p2＜∞next.

Using Lemma 2.7,we have

Obviously,

while f∈Lp1,p2(G2).Then,applying Lemma 2.2 again,we obtain

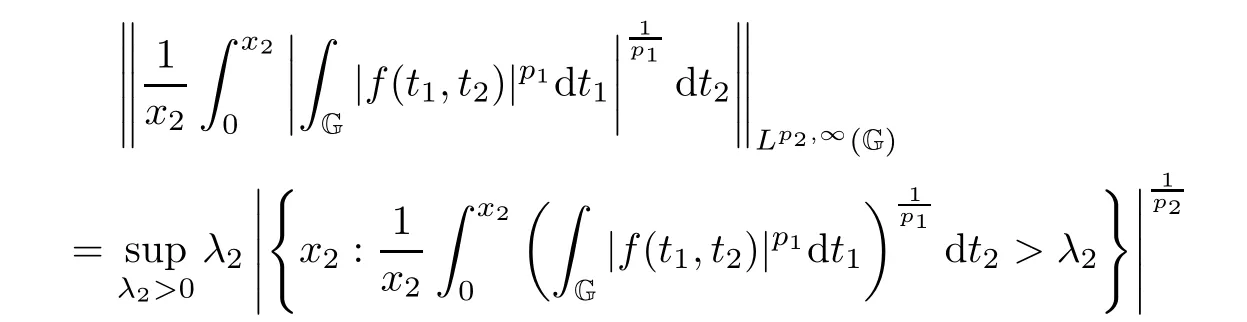
Combining(3.18),(3.19)with(3.20),it yields

for all f∈Lp1,p2(G2).

On the other hand,we will show that the constant 1 is the best possible.Denote χr=χ[0,r],r＞0.We also take f0(x)=χr(x),x∈G and choose F(x1,x2)=f0(x1)f0(x2).

While

from the proof of Theorem 3.1,we have the following estimate,

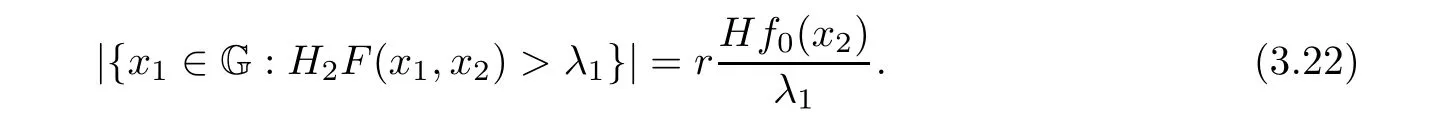
Evidently,

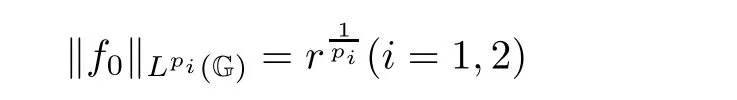
with i=1,2.It implies from(3.22)that

For 0 ＜ λ2＜ ‖f0‖Lp1(G),we also divide r into two cases:r ＞ x2and r≤ x2.A similar computation yields that

As ‖F‖Lp1,p2(G2)= ‖f0‖Lp1(G)‖f0‖Lp2(G),we can get from(3.24)

Combining(3.23)and(3.25),we obtain

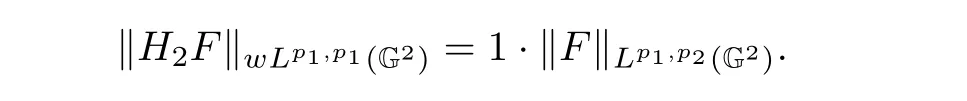
Then,we accomplish our proof.

Using the same method as in the proofs of the above two theorems,we now study the boundedness of the Hardy operator on product spaces from LP(Gn)to wLPI(Gn).

Theorem 3.3Suppose P=(p1,···,pn).When pisatisfies 1 ＜ pi＜ ∞,i∈ I and 1 ≤ pi＜ ∞,i∈ {1,···,n}I,the operator Hndefined by(1.4)is bounded from LP(Gn)to wLPI(Gn).Moreover,there holds

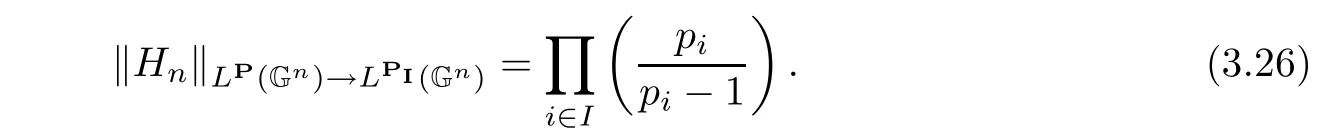
ProofWe just need to prove the case n=2 and I={1}because n≥3 is a simple generation of n=2.That is to say:we will prove that for p1＞1 and p2≥1,there holds

Noting

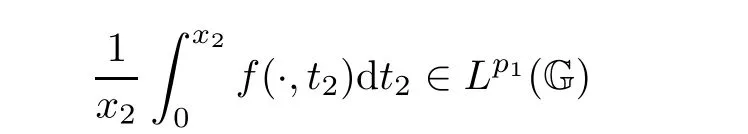
for all x2∈G while f∈Lp1,p2(G2),we can get from Theorem A

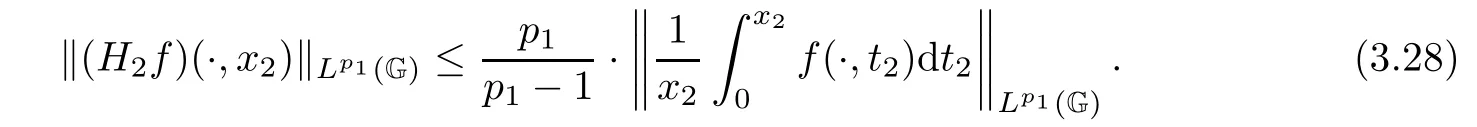
Theorem 3.2 tells us that when f∈Lp1,p2(G2),then there holds

Combining(3.28)with(3.29),we immediately obtain inequality(3.27).

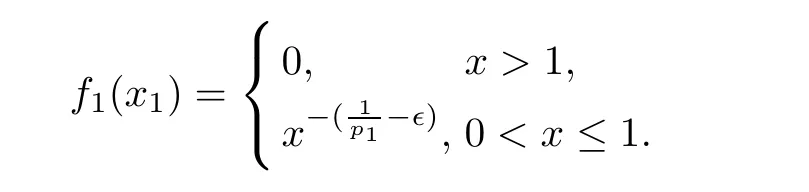
Obviously,

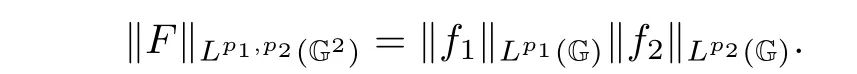
A direct computation yields

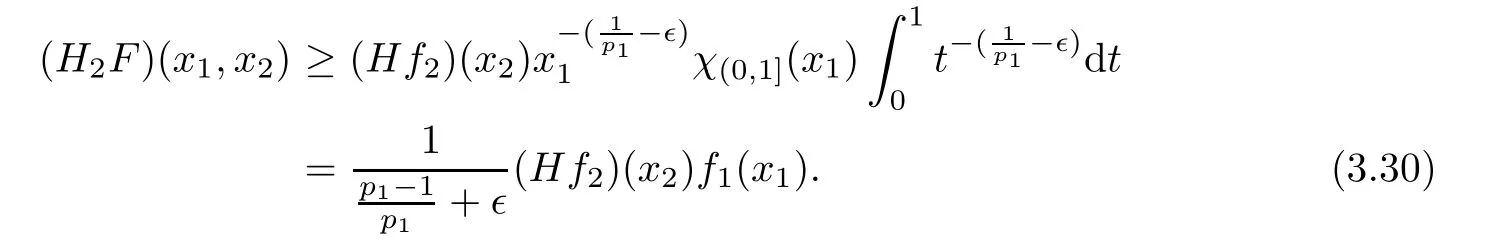
So,we can deduce from(3.30)that

From the proofs of Theorem 3.1 and Theorem 3.2,we have

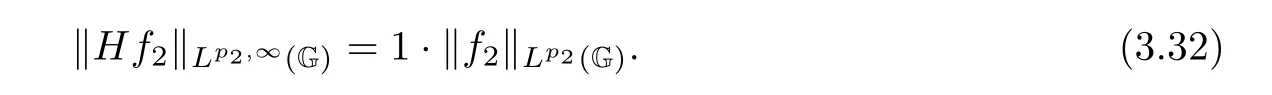
Combining(3.31)with(3.32),we get

Now,letting∈→0,it is immediately obtained that the constantis sharp.

[1]Hardy G H.Note on a theorem of Hilbert.Math Z,1920,6(3/4):314–317

[2]Faris W.Weak lebesgue spaces and quantum mechanincal binding.Duke Math,1976,43(2):365–273

[3]Christ M,Grafakos L.Best constants for two nonconvolution inequalities.Proc Amer Math Soc,1995,123(6):1687–1693

[4]Pachpatte B G.On multivariale Hardy type inequalities.An Stiint Univ Al I Cuza Iasi,1992,38:355–361

[5]Hardy G H,Littlewood J E,Polya G.Inequalities.2nd ed.Cambridge University Press,1952

[6]Carton-Lebrun C,Fosset M.Moyennes et quotients de Taylor dans BMO.Bull Soc Roy Sci Liege,1984,53:85–87

[7]Benyi A,Oh C T.Best constants for certain multilinear integral operators.J Inequal Appl,2006,2006:1–12

[8]Melas A.The best constant for the centered Hardy-Littlewood maximal inequality.Ann Math,2003,157:647–688

[9]Brannan D A,Hayman W K.Research problems in complex analysis.Bull London Math Soc,1989,21:1–35

[10]Wu D,Wang S M,Yan D Y.(L1,Lq)-boundedness for Hardy operators with power weight on n-dimensional space.Adv Math(China),2014,43:725–732

[11]Benedek A,Panzone R.The space Lp,with mixed norm.Duke Math,1961,28:301–324

[12]Benedek A,Calderón P,Panzone R.Convolution operators on Banach space valued functions.Proc Nat Acad Sci,1962,48:356–365

[13]Fefferman R,Stein E M.Singular integrals on product spaces.Adv Math,1982,45:117–143

[14]Journé J L.Calderón-Zygmund Operators on Product Spaces.Rev Mat Iberoamericana,1985,1(3):55–91

[15]Moen K.Linear and multilinear fractional operators:weighted inequalities,sharp bounds,and other properties.University of Kansas,2009

[16]Fernandez D L.Vector-valued singular integral operators on Lp-spaces with mixed norms and applications.Pacific J Math,1987,129(2):257–275

[17]Stefanov A,Torres R H.Calderón-Zygmund operators on mixed Lebesgue spaces and applications to null forms.J London Math Soc,2004,70(2):447–462

[18]Rudin W.Real and Complex Analysis.Tata McGraw-Hill Education,1987

[19]Hardy G H,Littlewood J E,Polya G.Inequalities.Cambridge University Press,1934

[20]Zhao F Y,Fu Z W,Lu S Z.Endpoint estimates for n-dimensional Hardy operators and their commutators,Sci China Math,2012,55(10):1977–1990

[21]Wang S M,Lu S Z,Yan D Y.Explicit constants for Hardy’s inequality with power weight on n-dimensional product spaces.Sci China Math,2012,55(12):2469–2480

[22]Lu S Z,Yan D Y,Zhao F Y.Sharp bounds for Hardy type operators on higher-dimensional product spaces.J Inequal Appl,2013,2013(1):148