ON A FIXED POINT THEOREM IN 2-BANACH SPACES AND SOME OF ITS APPLICATIONS∗

Janusz BRZDE¸K

Pedagogical University,Department of Mathematics,Podchor¸a˙zych 2,30-084 Kraków,Poland

E-mail:jbrzdek@up.krakow.pl

Krzysztof CIEPLINSKI†

AGH University of Science and Technology,Faculty of Applied Mathematics,Mickiewicza 30,30-059 Kraków,Poland

E-mail:cieplin@agh.edu.pl

1 Introduction

The following natural question arises in many areas of scientific investigations:what errors we commit replacing functions,that satisfy some equations only approximately,by the exact solutions to those equations.Some efficient tools to evaluate those errors can be found in the theory of Ulam’s stability.

Roughly speaking,nowadays we say that an equation is stable in some class of functions if any function from that class,satisfying the equation approximately(in some sense),is near(in some way)to an exact solution of the equation.The problem of stability of the Cauchy functional equation

was formulated for the first time by Ulam in 1940 for homomorphisms of metric groups,in a somewhat analogous way;a solution to it was published a year later by Hyers for Banach spaces(for details,see[1]).

In the last few decades,several stability problems of various(functional,differential,difference,integral)equations have been investigated by many mathematicians(see[1–8]for the comprehensive accounts of the subject),but mainly in classical spaces.However,the notion of an approximate solution and the idea of nearness of two functions can be understood in various,nonstandard ways,depending on the needs and tools available in a particular situation.One of such non-classical measures of a distance can be introduced by the notion of a 2-norm.

Recall that the concept of linear 2-normed space was introduced by S.Gähler in[9],and it seems that the first work on the Hyers-Ulam stability of functional equations in complete 2-normed spaces(that is,2-Banach spaces)is[10].After it some articles(see,for instance,[11–16])on the stability of other equations in such spaces have been published.

It has been shown that there is a close connection between some fixed point theorems and the Ulam stability theory(see,for example,[17–19]).The aim of this article is to prove a fixed point theorem in 2-Banach spaces(Theorem 1)and show that it has significant applications to the Ulam stability of some functional equations(Theorems 2 and 3).Let us mention yet that Theorem 1 corresponds to some outcomes from[20–23].

We present the stability results in 2-Banach spaces for some single variable equations(Theorem 2),but mainly we focus(see Theorem 3)on the stability of the most important functional equation in several variables,namely,the Cauchy equation,mentioned earlier;a lot of information about this equation(in particular,about its solutions,which are said to be additive mappings,and stability)and its applications can be found,for instance,in[24–26].

The last section of this article contains a result on the inhomogeneous Cauchy equation corresponding to some outcomes from[27–32],and a few corollaries corresponding to the hyperstability outcomes from[33–37](more information on the phenomenon of the hyperstability can be found in[4]).

Throughout this article,N stands for the set of all positive integers,N0:=N∪{0},and R+:=[0,∞).

2 Preliminaries

Let us recall(see,for instance,[38])that by a linear 2-normed space we mean a pair(X,‖·,·‖)such that X is an at least two-dimensional real linear space and ‖·,·‖ :X × X → R+is a function satisfying the following conditions:

(a) ‖x,y‖=0 if and only if x and y are linearly dependent;

(b) ‖x,y‖= ‖y,x‖for x,y∈ X;

(c) ‖x,y+z‖ ≤ ‖x,y‖+‖x,z‖ for x,y,z∈ X;

(d) ‖αx,y‖ =|α|‖x,y‖ for α ∈ R and x,y ∈ X.

A sequence(xn)n∈Nof elements of a linear 2-normed space X is called a Cauchy sequence if there are linearly independent y,z∈X such that

whereas(xn)n∈Nis said to be convergent if there exists an x ∈ X(called a limit of this sequence and denoted bywith

A linear 2-normed space in which every Cauchy sequence is convergent is called a 2-Banach space.

Let us also mention that in linear 2-normed spaces,every convergent sequence has exactly one limit and the standard properties of the limit of a sum and a scalar product are valid.Next,it is easily seen that we have the following property.

Lemma 2.1If X is a linear 2-normed space,x,y1,y2∈X,y1,y2are linearly independent,and

then x=0.

Let us yet recall a lemma from[16].

Lemma 2.2If X is a linear 2-normed space and(xn)n∈Nis a convergent sequence of elements of X,then

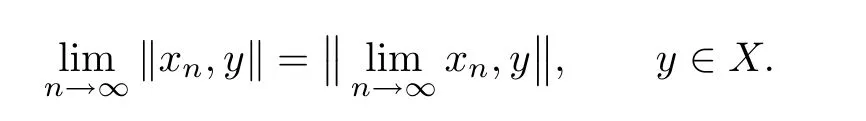
It is easy to check that(in view of the Cauchy-Schwarz inequality),if 〈·,·〉is a real inner product in a real linear space X,of dimension greater than 1,and

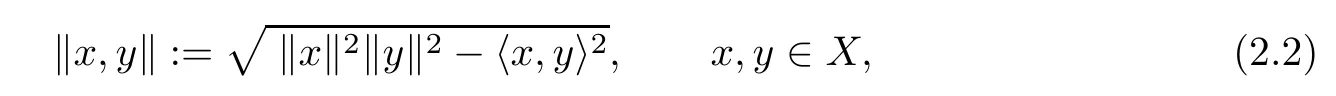
then conditions(a)–(d)are valid.Moreover,we have the following simple observation(we present it with a proof for the convenience of readers).

Proposition 2.3If(X,〈·,·〉)is a real Hilbert space,then X endowed with the 2-norm given by(2.2)is a 2-Banach space.

ProofTake a sequence(xn)n∈Nin X such that(2.1)holds with some linearly independent w,z∈X.Let{e1,e2}be a set of orthonormal vectors spanning the same subspace of X as the set{z,w}.Clearly,there are ai,bi∈R such that ei=aiz+biw for i=1,2.

Fix x ∈ X.Let e ∈ X be such that‖e‖ =1,〈e,x〉=0,and e:=c1e1+c2e2for some c1,c2∈R.Then,+=1 and

Furthermore,by the Cauchy-Schwartz inequality,

In this way,we shown that there is M＞0 with

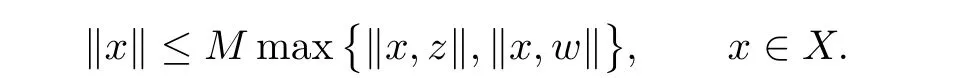
Hence,by(2.1),

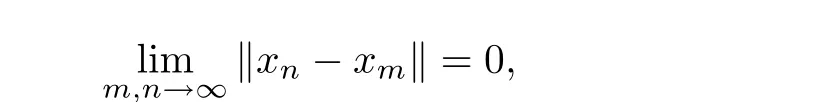
which means that there is^x∈X with

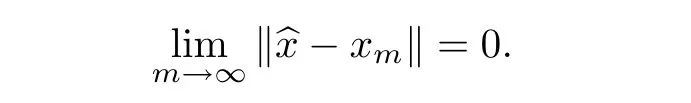
Consequently,

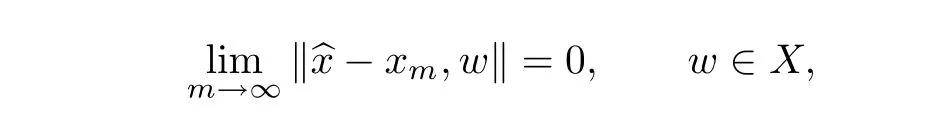
because

It is easily seen that(R2,‖·,·‖),where

is a simple example of a 2-Banach space.Clearly,the 2-norm given by(2.3)is a very particular case of(2.2)with the classical inner product in R2given by

3 Fixed Point Theorem

Let us introduce the following three hypotheses:

(H1)E is a nonempty set,(Y,‖·,·‖)is a 2-Banach space,Y0is a subset of Y containing two linearly independent vectors,j∈N,fi:E→E,gi:Y0→Y0,and Li:E×Y0→R+for i=1,···,j;

(H2)T:YE→YEis an operator satisfying the inequality

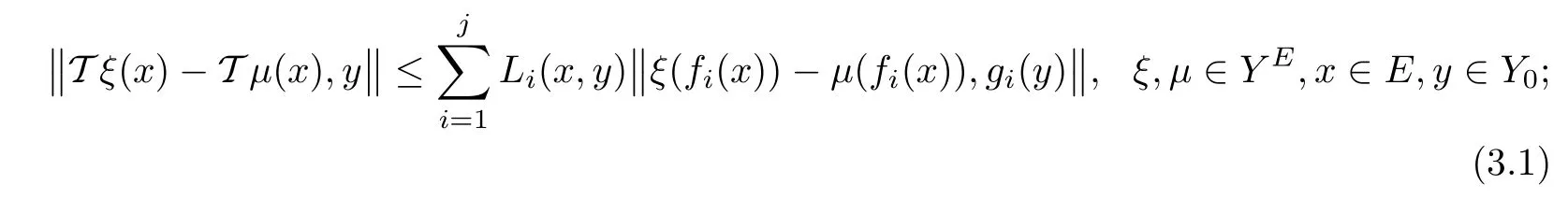
(H3)Λ:R+E×Y0→R+E×Y0is an operator defined by

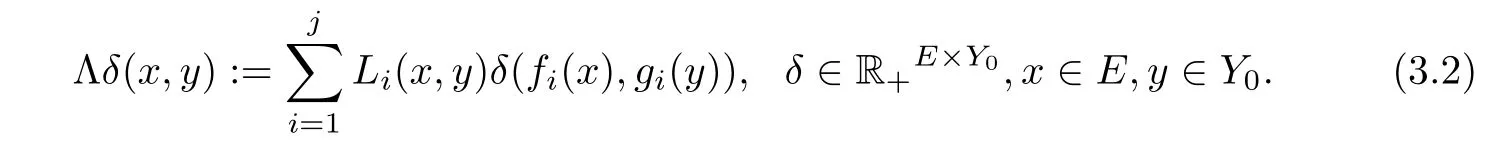
Now,we are in a position to present the above mentioned fixed point theorem.

Theorem 1Let hypotheses(H1)–(H3)hold and functions ε:E×Y0→ R+and ϕ :E → Y fulfill the following two conditions:

Then,there exists a unique fixed point ψ of T for which

Moreover,

ProofFirst,we show by induction that,for any n∈N0,

Clearly,by(3.3),the case n=0 is trivial.Now, fix an n∈N0and suppose that(3.7)is valid.Then,using(H2),for any x∈E and y∈Y0,we get

and therefore(3.7)holds for any n∈N0.

Next,note that,by(3.7)and(3.4),for any k∈N,n∈N0,x∈E,and y∈Y0,we have

Therefore,for any x ∈ E,((Tnϕ)(x))n∈Nis a Cauchy sequence,because Y0contains two linearly independent vectors.Thus,the fact that Y is a 2-Banach space implies that this sequence is convergent.Consequently,(3.6)defines a function ψ :E →Y.

Letting k→∞in(3.8),from Lemma 2.2 and(3.6),we obtain

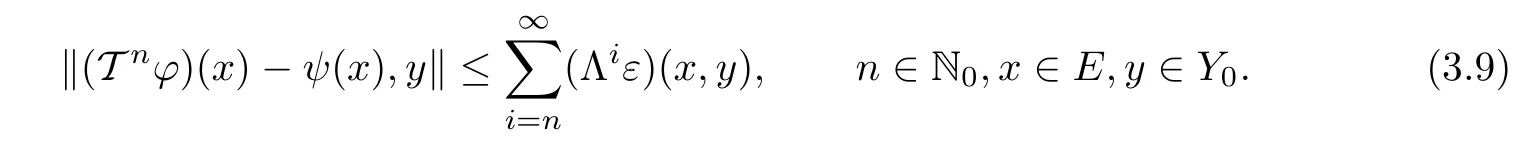
Putting n=0 in(3.9),we see that inequality(3.5)holds.Moreover,using(H2)and(3.9),we obtain

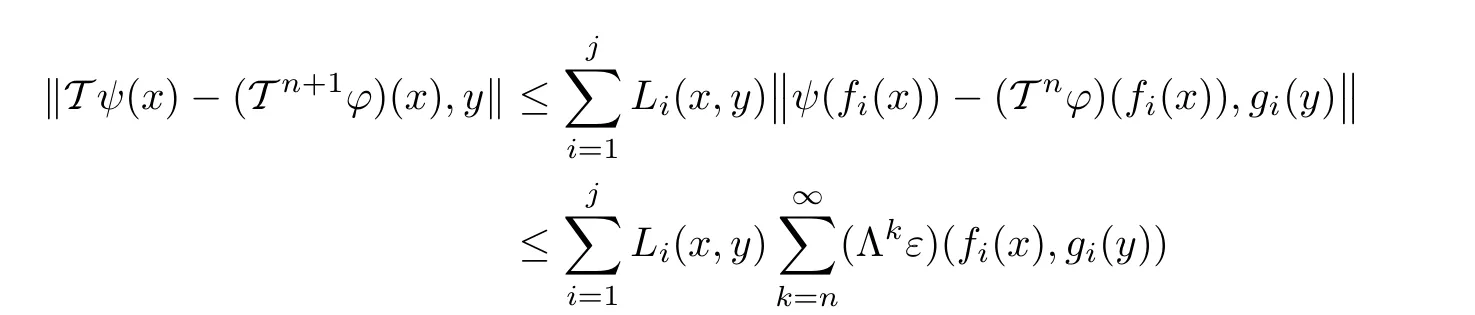
for n∈N0,x∈E,y∈Y0.Letting n→∞,we get T ψ=ψ,on account of(3.4)and Lemmas 2.1,2.2.

To prove the statement on the uniqueness of ψ,assume that ξ∈ YEis also a fixed point of T with

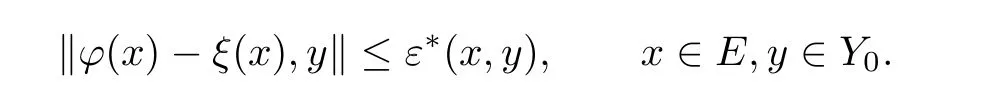
We show that for any n∈N0,we have

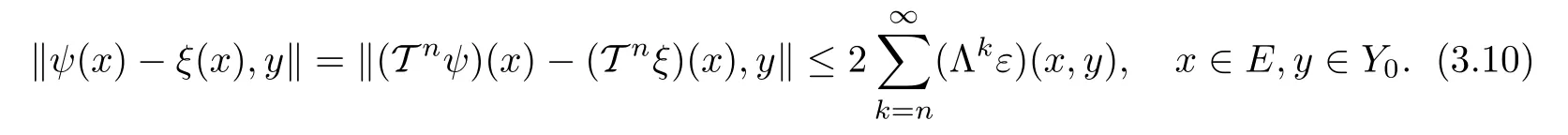
As

(3.10)holds for n=0.Next,assume that(3.10)is valid for an n∈N0.Then,by(H2),for any x∈E and y∈Y0,we get

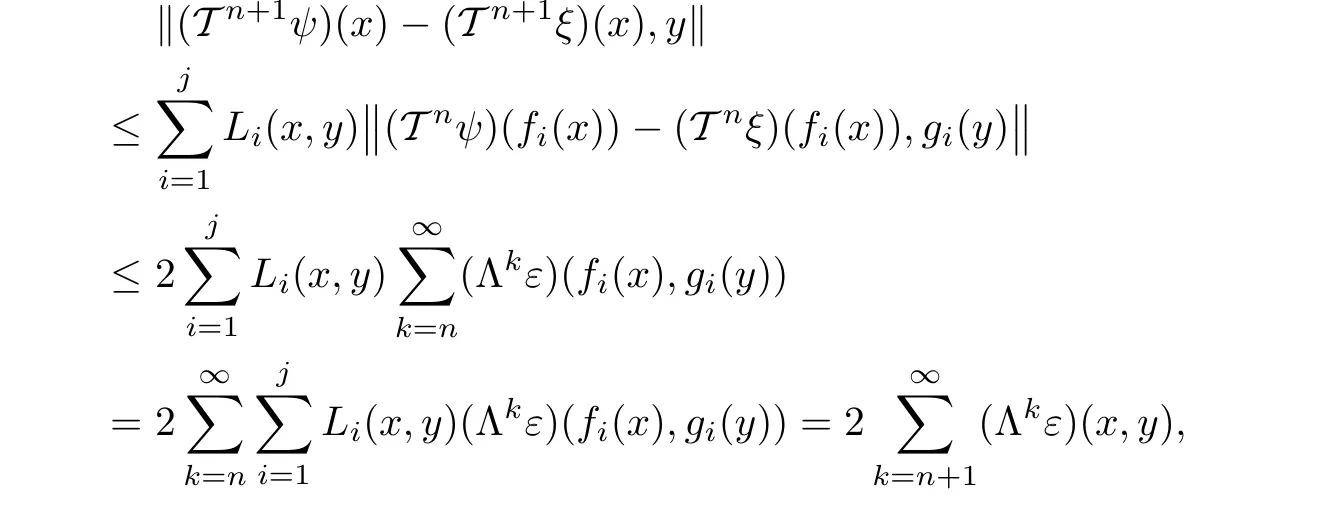
and thus(3.10)holds for any n∈N0.

Letting n→ ∞ in(3.10),from(3.4)and Lemma 2.1,we finally get ξ=ψ.

4 Two Consequences of Theorem 1

From Theorem 1,we obtain the following corollary.

Corollary 4.1Assume that hypotheses(H1)–(H3)are satisfied.If functions ε:E×Y0→R+,ϕ:E→Y and q:E×Y0→[0,1)are such that(3.3)holds,

and

then limit(3.6)exists and the function ψ :E →Y so defined is the unique fixed point of T with

ProofFrom(4.2),it follows that

and consequently,

Thus,condition(3.4)holds and our assertion follows from Theorem 1 and its proof.

It is easily seen that(4.2)holds for instance when

and ε:E × Y0→ R+is such that ε(fi(x),gi(y))≤ ε(x,y)for x ∈ E,y ∈ Y0,i=1,···,j.

In addition to hypotheses(H1)and(H3),we now make the following two assumptions:(H4)Φ:E×Yj→Y is an operator satisfying the inequality

for any x ∈ E,y ∈ Y0,and(y1,···,yj),(z1,···,zj)∈ Yj;

(H5)T:YE→YEis an operator defined by

It is easily seen that then hypothesis(H2)holds.Consequently,the following corollary can be deduced from Theorem 1.

Theorem 2Assume that hypotheses(H1)and(H3)–(H5)are fulfilled,ε:E ×Y0→ R+satisfies(3.4),and ϕ:E → Y is such that

Then,limit(3.6),with T given by(4.4),exists and the function ψ :E → Y is the unique solution of the functional equation

such that inequality(3.5)holds.

ProofLet us note that inequality(4.5)implies(3.3).Therefore,Theorem 1 can be applied and the function ψ defined by(3.6)satisfies(3.5)and is the unique such fixed point of T,which means that ψ is a solution of(4.6).

5 Main Stability Result

In what follows,(Y,‖·,·‖)stands for a 2-Banach space and Y0is a subset of Y containing two linearly independent vectors.Given a group(X,+),we denote by AutX the family of all its automorphisms and,for simplicity,we write

and

We also say that U⊂AutX is commutative provided

The following theorem is our main stability result.

Theorem 3Assume that(X,+)is a commutative group,X0:=X{0}/=Ø,H:×Y0→R+,and

where,for any u∈AutX,

If f:X→Y fulfils then,for any nonempty and commutative U⊂l(X),there is a unique additive mapping T:X → Y such that

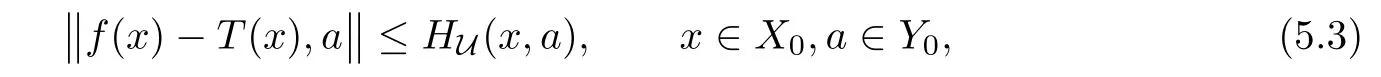
where

ProofFix a nonempty and commutative U ⊂ l(X).Clearly,(5.2)with x replaced by u′x and y=ux gives

For any u ∈ U,we define operators Tu:YX0→ YX0and Λu:R+X0×Y0→ R+X0×Y0by formulas

Note that,for any u∈U,Λ:=Λuhas form(3.2)with E:=X0,j=2,L1(x,a)=1=L2(x,a),g1(a)=a=g2(a),f1(x)=u′x and f2(x)=ux.

Moreover,(5.4)can be rewritten as

(here and in the sequel f denotes the restriction of the function f:X→Y to the set X0)and we have

for any ξ,µ ∈ YX0,x∈ X0,u∈ U,a∈ Y0.Consequently,for any u∈ U,also(3.1)holds for T:=Tu.

Finally,by the definition of λ(u),we have

whence,by induction,we easily get

and therefore,

Now,we apply Theorem 1(for ε := εuand ϕ =f),and on account of it,for any x ∈ X0and u∈U,there exists the limit

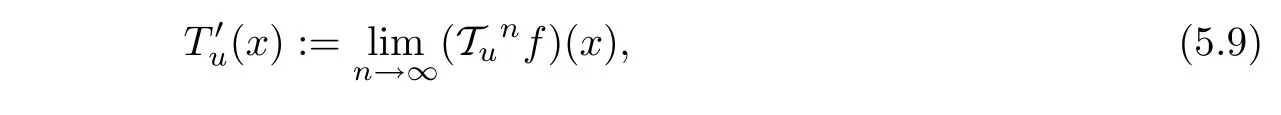
and for any u∈U,the function Tu:X→Y,given by the formula

is a solution of the functional equation

Now,we show that

for any n∈N0,u∈U,a∈Y0and x,y∈X0with x+y∈X0.

As the case n=0 follows immediately from(5.2), fix an n∈N0and assume that(5.12)is valid for any u∈U,a∈Y0,and x,y∈X0with x+y∈X0.Then,by(5.8),we get

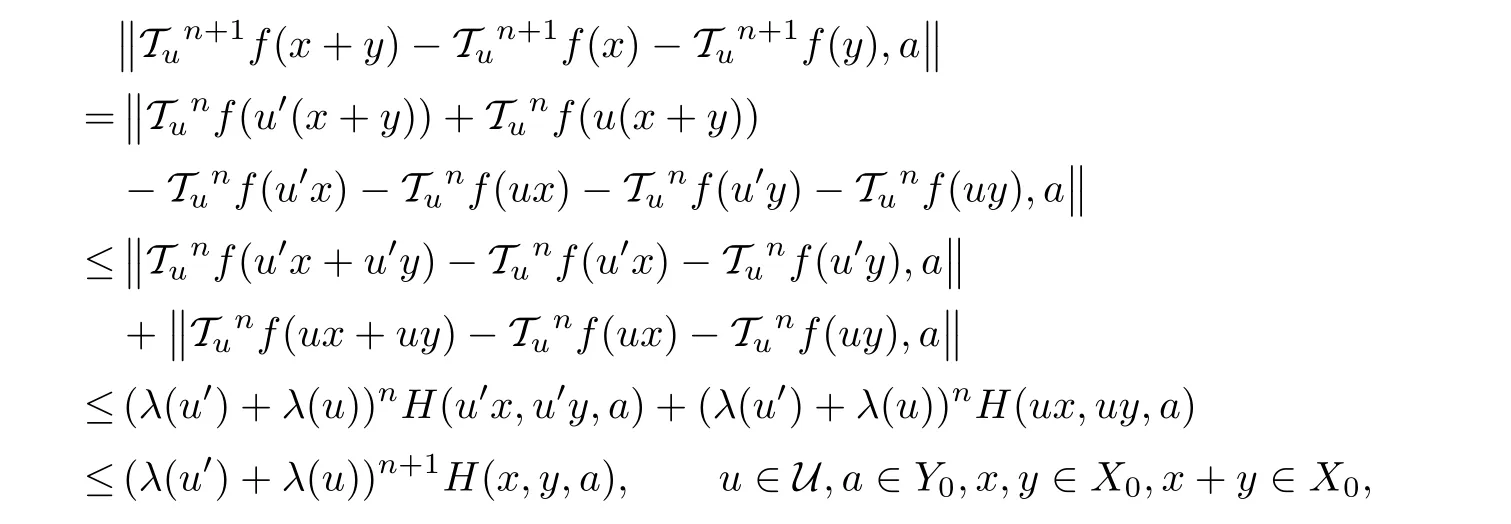
and thus(5.12)holds for any n∈N0,u∈U,a∈Y0,and x,y∈X0with x+y∈X0.

Letting n→∞in(5.12)and using Lemmas 2.1 and 2.2,we see that

We show that for any u∈U,the mapping Tuis in fact additive.Note that,by(5.13),to this end it suffices to consider the case y=−x.Fix u∈U and x∈X0(the case x=0 is trivial).Then,according to(5.13),we have

which implies that Tu(x)+Tu(−x)=0 and therefore

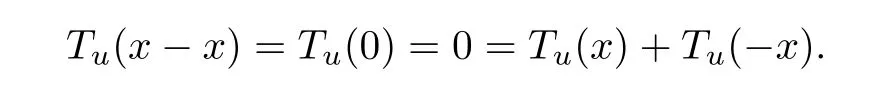
Next,we prove that every additive mapping A:X→Y satisfying the inequality

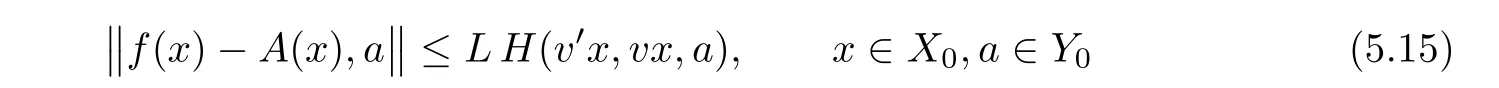
with some L＞0 and v∈U,is equal to Twfor any w∈U.To do this, fix v,w∈U,L＞0 and let A:X→Y be an additive mapping satisfying(5.15).Note that,by(5.10)and(5.15),there is an L0＞ 0(one can take,for example,L0:=max{1,L(1−λ(w′)−λ(w))})such that

for x∈X0and a∈Y0.Observe also that A and Tware solutions of equation(5.11)for any u∈U,because they are additive.

We show that,for any j∈N0,

The case j=0 is exactly(5.16).Fix a j∈N0and assume that(5.17)holds.Then,in view of(5.8),we get

for any x∈X0,a∈Y0,and thus(5.17)is valid for any j∈N0.

Letting j→∞in(5.17)and using Lemma 2.1,we see that

which together with the additivity of A and Twgives A=Tw.

Let us finally note that we have also proved that Tu=Twfor any u∈U(on account of(5.10)),and therefore,

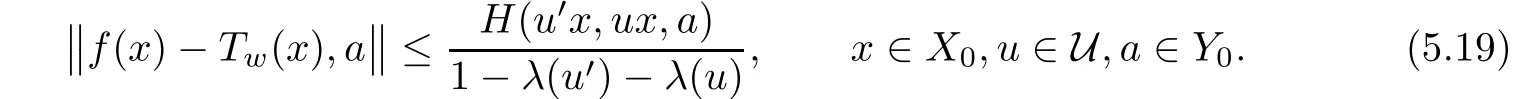
Hence,we get(5.3)with T:=Tw.

6 Some Consequences of Theorem 3

Theorem 3 yields the following corollary.

Corollary 6.1Let X,X0,and H be as in Theorem 3.If there exists a nonempty and commutative U⊂l(X)such that

and

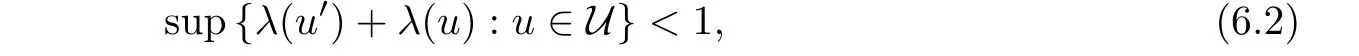
then every function f:X→Y satisfying(5.2)is additive.

ProofSuppose that f:X→Y satisfies(5.2).Then,by Theorem 3,there exists an additive mapping T:X→Y such that(5.3)holds.Since,in view of(6.1)and(6.2),HU(x,a)=0 for x∈X0and a∈Y0,this means that f(x)=T(x)for x∈X0.Hence,

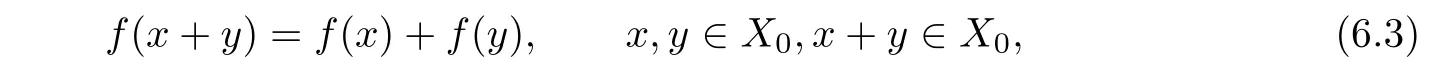
and therefore f is additive(see the proof of the additivity of Tuin the proof of Theorem 3).□

The next corollary corresponds to the results on the inhomogeneous Cauchy equation from[27–32].

Corollary 6.2Let X,X0,and H be as in Theorem 3,and F:X2→Y.Suppose also that

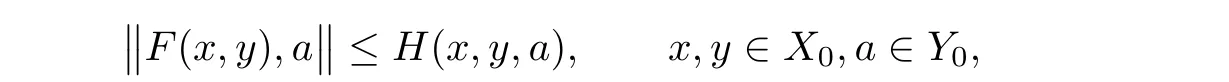
F(x0,y0)/=0 for some x0,y0∈X0and there exists a nonempty and commutative U⊂l(X)such that(6.1)and(6.2)hold.Then,the inhomogenous Cauchy equation

has no solution in the class of functions f:X→Y.

ProofSuppose that f:X→Y is a solution of(6.4).Then,

Consequently,by Corollary 6.1,f is additive,and therefore

which is a contradiction.

Remark 6.3We have excluded x=0 and y=0 from the domain of H in Theorem 3 for the reason that can be easily seen from the following natural example.

In the rest of this article,X and X0are as in Theorem 3,Z is a 2-normed space,Z1,Z2are linear subspaces of Z with Z1∩Z2={0},Z0:=Z2{0},η,χ :X → Z1are additive injections,and g1,g2:Y0→Z0.Moreover,for any n∈Z,we defineµn:X→X by

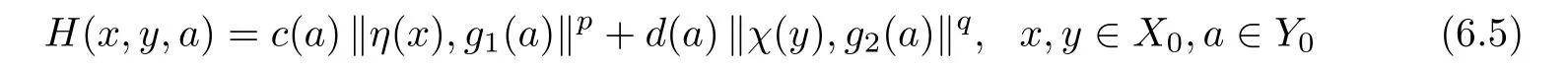
with some p,q＜0 and c,d:Y0→R+.Then,

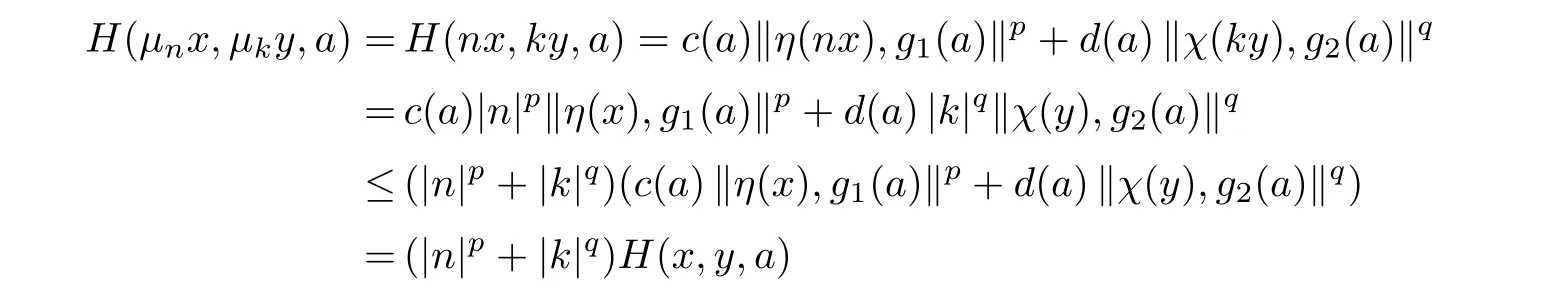
for any x,y∈X0,a∈Y0andµk,µn∈AutX.Hence,if there exists an N ＞ 1 such thatµn,∈AutX for n∈N with n＞N,then

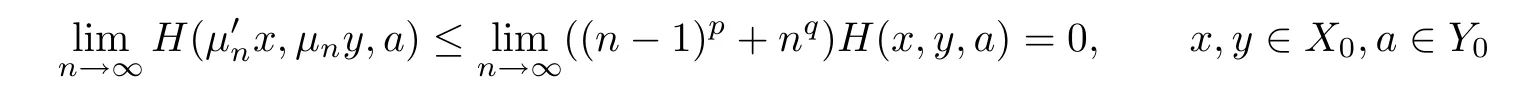
and there is an M＞N for which

Moreover,it is easily seen that conditions(6.1)and(6.2)are then fulfilled with

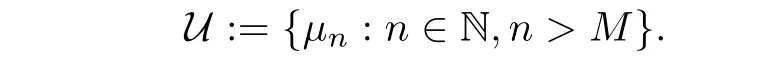
Therefore,by Corollary 6.1,we have the following result corresponding to the hyperstability outcomes from[33,34,37].

Corollary 6.4Let H be given by(6.5)with some p,q＜0 and c,d:Y0→R+.If there exists an N ＞ 1 such thatµn,∈AutX for n∈N with n＞N,then every mapping f:X→Y satisfying(5.2)is additive.

Analogous conclusion we get when H is given by

with some c:Y0→R+and p,q∈R such that p,q＜0,because

for any x,y∈X0,a∈Y0andµk,µn∈AutX.

Therefore,we also have the following hyperstability result,which corresponds to some extent to the main outcome of[35].

Corollary 6.5Let H be given by(6.6)with some c:Y0→R+and p,q∈R such that p,q＜ 0.If there exists an N ＞ 1 such thatµn,∈AutX for n∈N with n＞N,then every mapping f:X→Y satisfying(5.2)is additive.

It is easily seen that another example of the function H satisfying(6.1)and(6.2)is given by

with some p,q＞0,r＜0,and c,d:Y0→(0,∞),because

for any x,y∈X0,a∈Y0,andµk,µn∈ AutX.

Thus,we get the following corollary.

Corollary 6.6Let H be given by(6.7)with some p,q＞0,r＜0,and c,d:Y0→(0,∞).If there exists an N ＞ 1 such thatµn,∈AutX for n∈N with n＞N,then every mapping f:X→Y satisfying(5.2)is additive.

We finish this article with a result that corresponds to some outcomes from[36].

Corollary 6.7Let X be divisible by 2,H be given by(6.5)with some c,d:Y0→R+and p,q∈R such that 1＜p＜q.If f:X→Y satisfies(5.2),then there exists a unique additive mapping T:X→Y for which

ProofLet f:X→Y satisfy(5.2)and u0:X→X be given by

Then,u0=and λ(u0) ≤ 2−p.Consequently,by Theorem 3 with U={u0},there is a unique additive T:X→Y such that

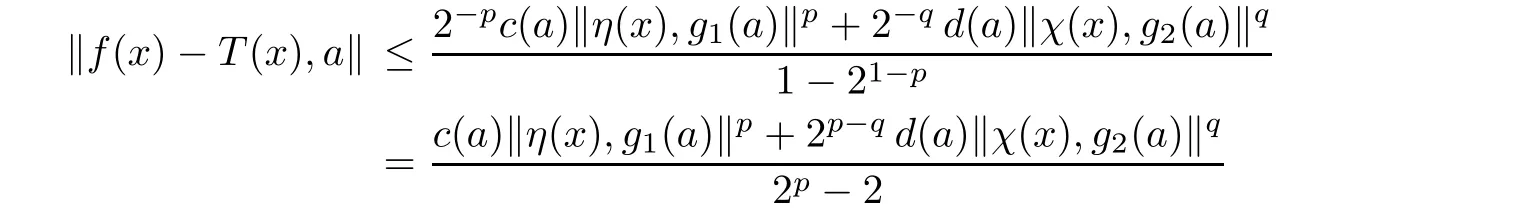
for any x∈X0and a∈Y0.

[1]Hyers D H,Isac G,Rassias Th M.Stability of Functional Equations in Several Variables.Boston:Birkhäuser,1998

[2]Agarwal R P,Xu B,Zhang W.Stability of functional equations in single variable.J Math Anal Appl,2003,288(2):852–869

[3]Brillouët-Belluot N,Brzd¸ek J,Cieplínski K.On some recent developments in Ulam’s type stability.Abstr Appl Anal,2012,Art ID 716936

[4]Brzd¸ek J,Cieplínski K.Hyperstability and superstability.Abstr Appl Anal,2013,Art ID 401756

[5]Brzd¸ek J,Cieplínski K,Lesniak Z.On Ulam’s type stability of the linear equation and related issues.Discrete Dyn Nat Soc,2014,Art ID 536791

[6]Forti G L.Hyers-Ulam stability of functional equations in several variables.Aequationes Math,1995,50(1/2):143–190

[7]Jung S M.Hyers-Ulam-Rassias Stability of Functional Equations in Nonlinear Analysis.New York:Springer,2011

[8]Miura T,Takahasi S,Choda H.On the Hyers-Ulam stability of real continuous function valued differentiable map.Tokyo J Math,2001,24(2):467–476

[9]Gähler S.Lineare 2-normierte Räume.Math Nachr,1964,28:1-43

[10]Gao J.On the stability of the linear mapping in 2-normed spaces.Nonlinear Funct Anal Appl,2009,14(5):801–807

[11]Cho Y J,Park C,Eshaghi Gordji M.Approximate additive and quadratic mappings in 2-Banach spaces and related topics.Int J Nonlinear Anal Appl,2012,3(2):75–81

[12]Chung S C,Park W G.Hyers-Ulam stability of functional equations in 2-Banach spaces.Int J Math Anal(Ruse),2012,6(17/20):951–961

[13]Cieplínski K.Approximate multi-additive mappings in 2-Banach spaces.Bull Iranian Math Soc,2015,41(3):785–792

[14]Cieplínski K,Surowczyk A.On the Hyers-Ulam stability of an equation characterizing multi-quadratic mappings.Acta Mathematica Scientia,2015,35B(3):690–702

[15]Cieplínski K,Xu T Z.Approximate multi-Jensen and multi-quadratic mappings in 2-Banach spaces.Carpathian J Math,2013,29(2):159–166

[16]Park W G.Approximate additive mappings in 2-Banach spaces and related topics.J Math Anal Appl,2011,376(1):193–202

[17]Brzd¸ek J,Cǎdariu L,Cieplínski K.Fixed point theory and the Ulam stability.J Funct Spaces,2014,Art ID 829419

[18]Cieplínski K.Applications of fixed point theorems to the Hyers-Ulam stability of functional equations-a survey.Ann Funct Anal,2012,3(1):151–164

[19]Xu B,Brzd¸ek J,Zhang W.Fixed-point results and the Hyers-Ulam stability of linear equations of higher orders.Pacific J Math,2015,273(2):483–498

[20]Brzd¸ek J,Chudziak J,Páles Zs.A fixed point approach to stability of functional equations.Nonlinear Anal,2011,74(17):6728–6732

[21]Brzd¸ek J,Cieplínski K.A fixed point approach to the stability of functional equations in non-Archimedean metric spaces.Nonlinear Anal,2011,74(18):6861–6867

[22]Cǎdariu L,Gǎvrut¸a L,Gǎvrut¸a P.Fixed points and generalized Hyers-Ulam stability.Abstr Appl Anal,2012,Art ID 712743

[23]Bahyrycz A,Brzd¸ek J,Jab lońska E,Olko J.On functions that are approximate fixed points almost everywhere and Ulam’s type stability.J Fixed Point Theory Appl,2015,17(4):659–668

[24]Kannappan Pl.Functional Equations and Inequalities with Applications.New York:Springer,2009

[25]Kuczma M.An Introduction to the Theory of Functional Equations and Inequalities.Cauchy’s Equation and Jensen’s Inequality.Basel:Birkhäuser Verlag,2009

[26]Sahoo P K,Kannappan Pl.Introduction to Functional Equations.Boca Raton:CRC Press,2011

[27]Borelli Forti C.Solutions of a nonhomogeneous Cauchy equation.Rad Mat,1989,5(2):213–222

[28]Ebanks B R.Generalized Cauchy difference functional equations.Aequationes Math,2005,70(1-2):154–176

[29]Ebanks B R.Generalized Cauchy difference equations.II.Proc Amer Math Soc,2008,136(11):3911–3919

[30]Ebanks B R,Kannappan Pl,Sahoo P K.Cauchy differences that depend on the product of arguments.Glasnik Mat Ser III,1992,27(47)(2):251–261

[31]Fenyö I,Forti G-L.On the inhomogeneous Cauchy functional equation.Stochastica,1981,5(2):71–77

[32]Járai A,Maksa Gy,Páles Zs.On Cauchy-differences that are also quasisums.Publ Math Debrecen,2004,65(3-4):381–398

[33]Brzd¸ek J.Hyperstability of the Cauchy equation on restricted domains.Acta Math Hungar,2013,141(1-2):58–67

[34]Brzd¸ek J.Remarks on hyperstability of the Cauchy functional equation.Aequationes Math,2013,86(3):255–267

[35]Brzd¸ek J.A hyperstability result for the Cauchy equation.Bull Aust Math Soc,2014,89(1):33–40

[36]Isac G,Rassias Th M.Functional inequalities for approximately additive mappings//Rassias Th M,Tabor,J Stability of Mappings of Hyers-Ulam Type.Palm Harbor:Hadronic Press,1994:117–125

[37]Piszczek M.Remark on hyperstability of the general linear equation.Aequationes Math,2014,88(1-2):163–168

[38]Freese R W,Cho Y J.Geometry of Linear 2-normed Spaces.Hauppauge,NY:Nova Science Publishers,Inc,2001