静压气浮轴承工程设计方法研究

王春喜 姜云翔 张凌东 吴 跃 王 强 冯伟利

(1.北京航天计量测试技术研究所，北京100076； 2.火箭军驻首都航天机械公司军事代表室，北京 100076)

1 引 言

静压气浮轴承是惯性器件测试平台回转支撑轴系的关键部件，在惯性器件测试过程中，提供准确的角度基准，其承载能力和回转精度对惯性器件测试的准确性有着重要的影响[1～3]。

目前，静压气浮轴承计算复杂，设计过程较为繁琐，国内外学者对静压气浮轴承的承载能力计算、刚度计算、精度计算等方面做了大量研究工作，并取得很多成果[4～7]。本文在此基础上，提出一种简化的工程计算方法，有助于简化设计过程，提高系统设计效率。

2 静压气浮轴承承载能力与刚度简化计算模型建立

静压气浮轴承结构如图1所示，双排供气，单排节流孔数为n，轴承半径为R，直径为D，供气孔直径为d，整个轴颈长为L，供气孔与端面之间的距离为l，轴承间隙为h0，偏心距为e，气膜厚度为h，供气压强为P0，节流孔口压强分布为P，环境压强为Pa，温度为T。

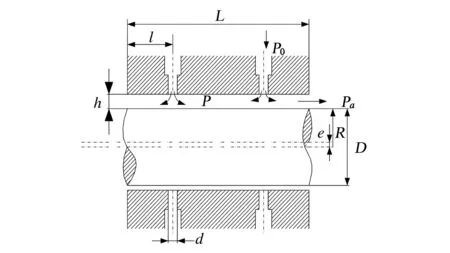
图1 静压气浮轴承结构示意图Fig.1 Structure diagram of the aerostatic pressure gas bearing

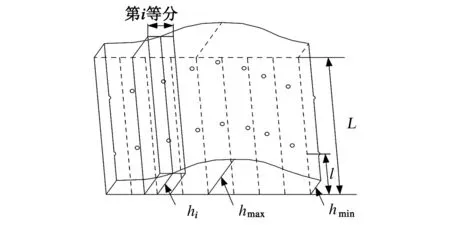
图2 展开成平面后气膜厚度分布示意图Fig.2 Distribution diagram of the gas film thickness after flattening

由于径向静压气浮轴承的气膜厚度远小于轴承半径，可以忽略圆柱表面曲率的影响，把径向静压气浮轴承的圆柱形轴承气膜展开成平面，如图2所示。将展开的气膜按照节流孔数在圆周方向上分为n等份，每一等份的宽度为πD/n。假设气膜厚度在每一等份中为常数，数值为该节流孔处的气膜厚度值hi(i=1,2,3......)，其分布为余弦规律，如(1)式所示

hi=h0(1-εcosαi)

(1)

式中：h0——最大轴承气膜厚度；ε——偏心率；αi——第i个节流孔离基准线的周向角度位置。为方便计算，对任意等分i做如下假设：

(1)相邻两节流孔之间无气体流动，气体自小孔流出后，立即充满该等份的全宽度，使气体在每个等份内呈一维流动，符合线性气源假设。

(2)每等份内两节流孔间压强相等，其值为该等份节流孔节流后压强Pdi。

(3)气体无环向流动，只是沿轴向流向端面，其压强由孔节流后Pdi降至端面的环境压强Pa。

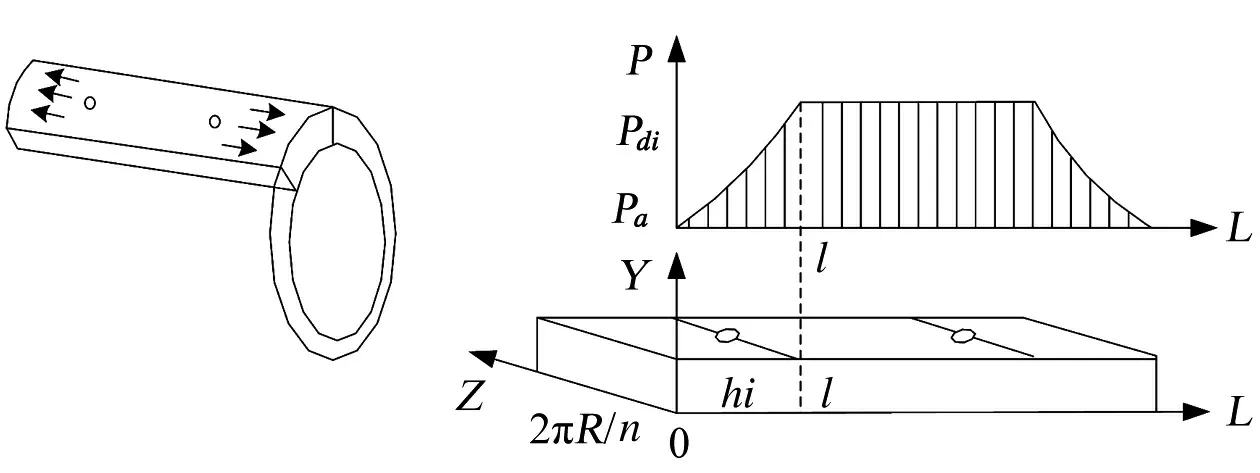
图3 第i等分内的气体压力分布示意图Fig.3 Distribution fiagram of fthe gas pressure in parts i

(4)气体为等温层流流动，即气膜内气体温度与环境温度相等，且气膜内气体温度与气源温度相同。

在此假设条件下，存在以下关系

状态方程为

式中：ρ——气体密度，气体沿周向无流动。另设粘性系数η为常值(η与温度有关)，P只与x有关

运动方程为

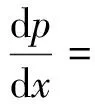
质量连续方程为

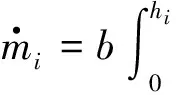
(4)

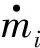
单个节流孔质量流量方程为

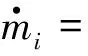
(5)

式中：φ——流量系数，是理论值偏离实际值的修正系数，随p/p0变化，取值0.8；Pa——断面的环境压力；A——节流面积(对于简单孔式节流器，A=πd2/4，对于环行孔式节流器，没有气腔情况下，当hd/4时，A=πd2/4)；ψ——小孔流量速度系数[8]。

由方程(2)(3)(4)(5)可得以下关系

式中：Px——在图3中坐标值为x点的压强，当x=l时，Px=Pa，则(6)式成为

将(7)式除以(6)式，经整理得

为求得气体压强的合力，观察图4所示的第i等份，图中ab为第i等份弧长，其上作用的气体压强是沿弧ab法向的，因而单位轴向长度的合力在过该等分中点半径上的投影为

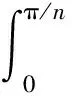
(9)

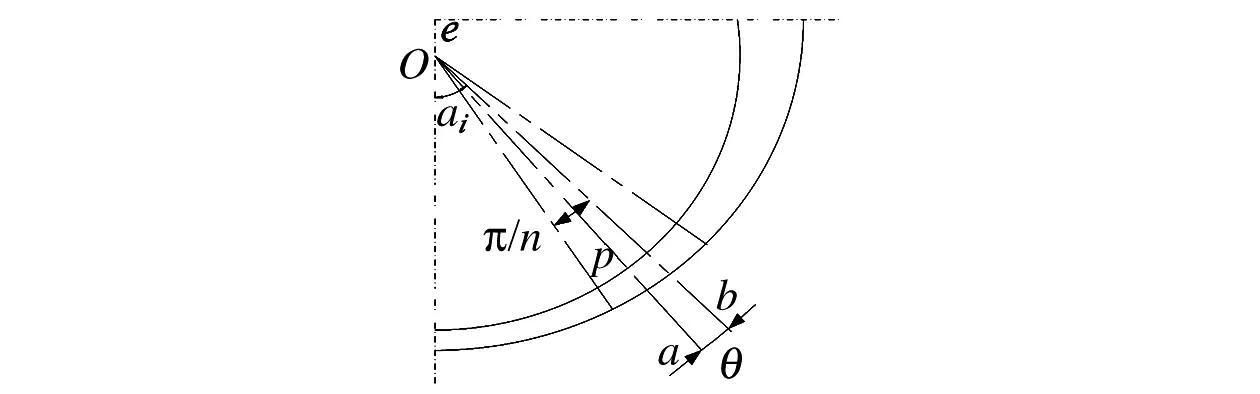
图4 压强投影示意图Fig.4 Diagram of the pressure proiection

因在任意等份中，全宽度b上压强不变，结合图4上压强分布假设，第i等份总合力可写为

由于合力的方向与过该等份中点的半径重合，它与基准线的夹角为αi(i=1,2,3......n)，整个轴的承载能力，可表示为

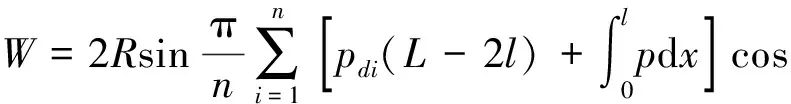
(11)

将(8)式带入(11)式，进行积分，考虑扩散效应和环流效应修正后[8,9]，可得承载力最终表达式为

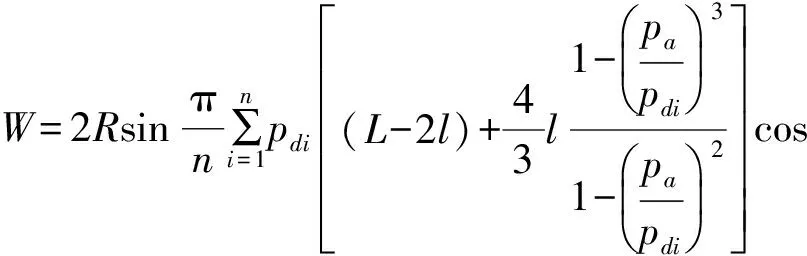
(12)

式中：fw——扩散效应和环流效应修正系数。

对应不同的偏心距e，可以求解相应的承载力W和轴承刚度，在计算轴承刚度时，如果计算点足够密，可以用差分式代替微分式计算刚度KW，如式(13)所示

式中：Δe——相邻偏心点的偏心增量；W(e+Δe)和W(e)——分别为(e+Δe)和e点的承载能力。

可基于Matlab进行迭代求解，在求解气膜间隙的压强分布、承载力的计算过程中，最为关键的参数为每个等分内节流后的压强pdi，其计算表达式为分段的隐函数

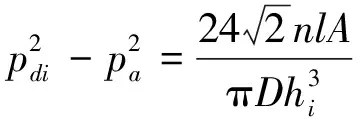
(14)

因此，采用Matlab计算软件进行编程求解，对于隐函数的方程采用二分法进行数值求解，总的编程迭代流程图如图5所示。

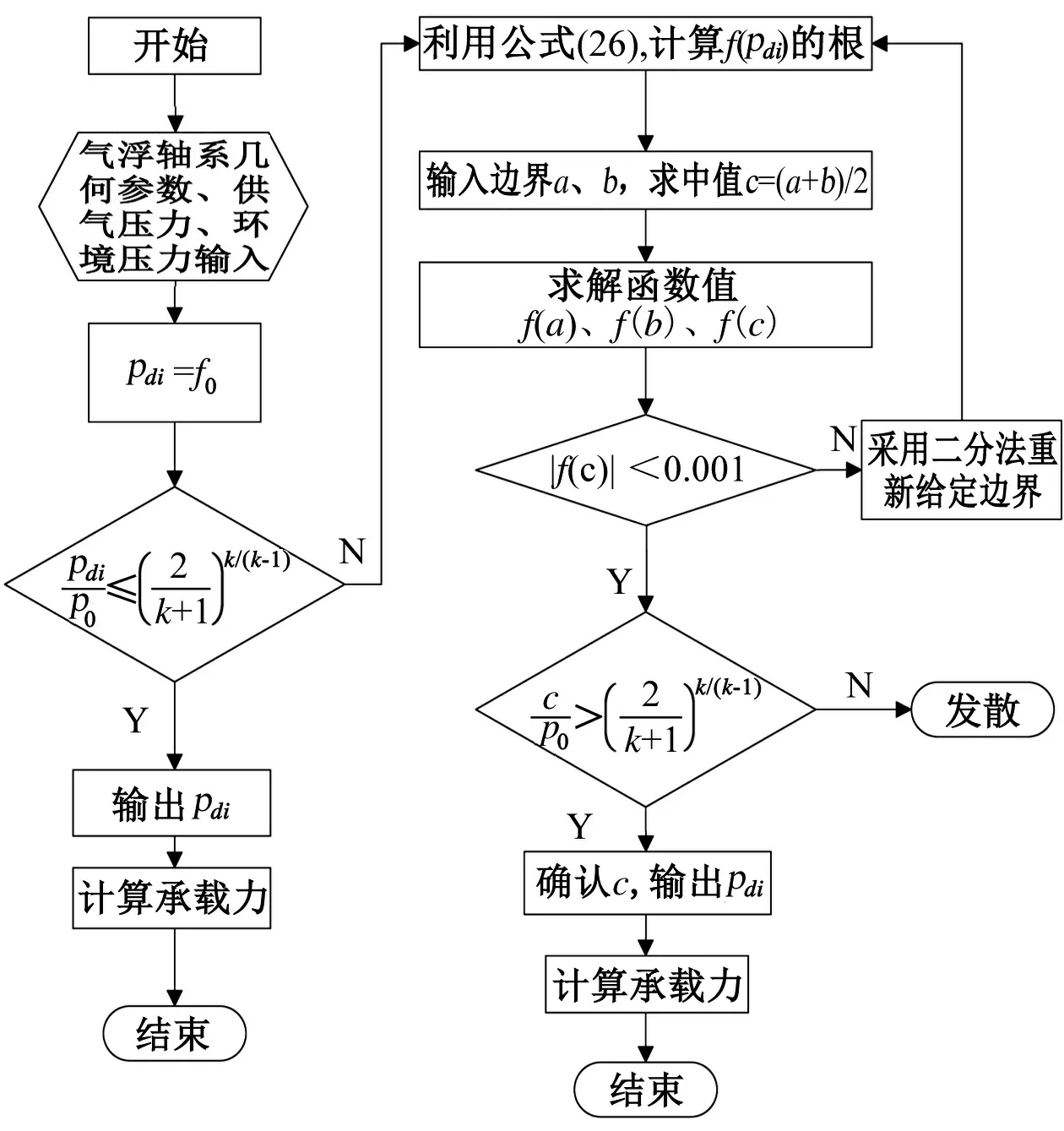
图5 Matlab迭代计算流程图Fig.5 Flow diagram of matlab iterative computations

图5中函数如下所示

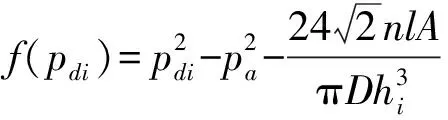
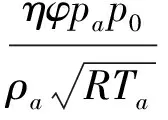
3 静压气浮轴系参数设计

3.1 总体结构设计

本文气浮轴系设计指标要求负载能力为40kg，轴承内径不大于200mm；采用气体静压径向轴承、气体静压止推轴承、主轴组合而成，如图6 所示。

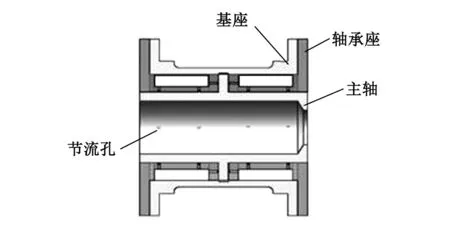
图6 气浮轴承设计示意图Fig.6 Diagram of gas bearing design

为提高轴系的径向承载能力和刚度，设计采用双气体静压径向轴承对称布置；闭式气体静压止推轴承位于两径向轴承的中间位置，有效降低了结构总体尺寸。

3.2 径向轴承设

为了提高轴系的径向承载能力和角刚度，轴系采用双径向轴承的结构，关于止推轴承对称布置，见图7所示。

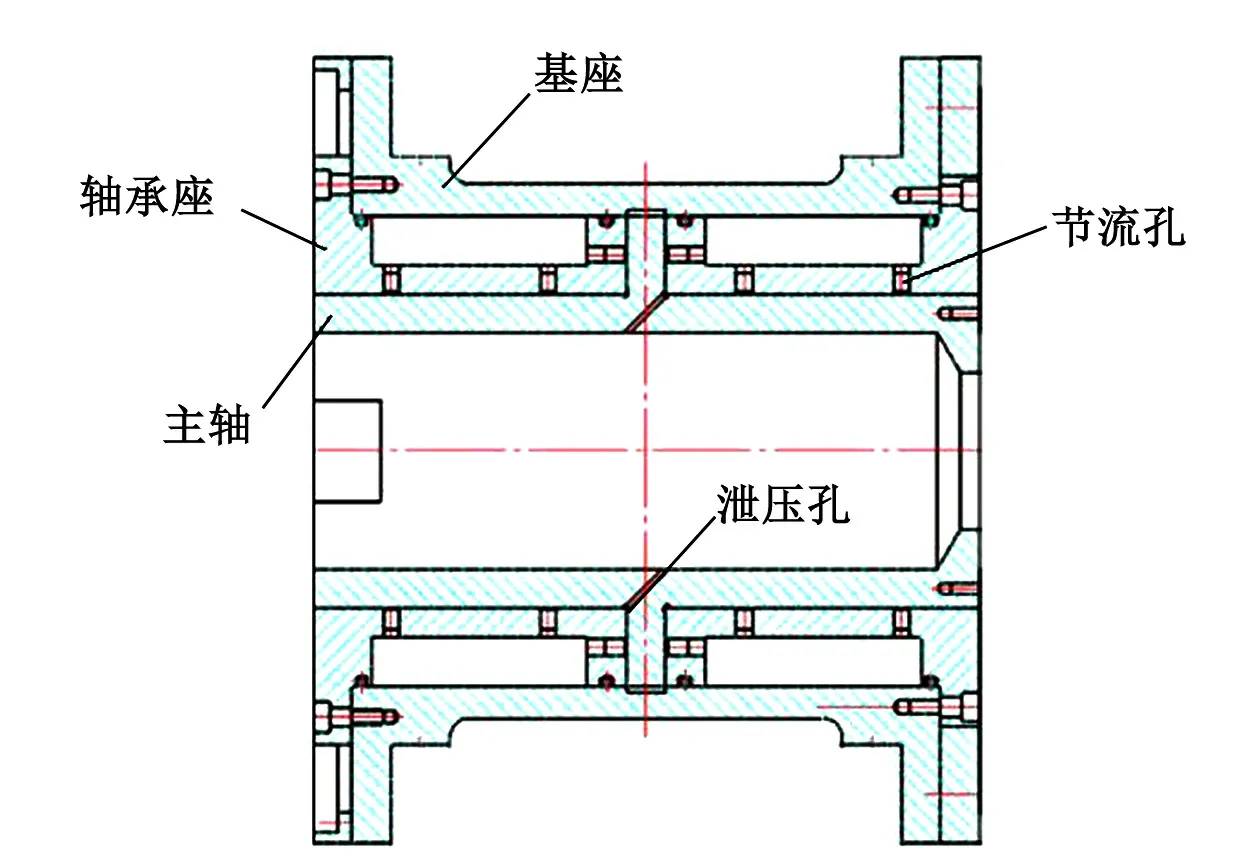
图7 径向轴承结构图Fig.7 Structure diagram of radial bearing

两气体静压径向轴承具有相同结构参数、节流器参数及供气压强。轴承内径为160mm，长度为160mm；节流孔排数2排，每排12个节流孔；节流孔喉孔直径为0.2mm；单边径向气膜间隙13μm；供气压强0.7Mpa。轴系径向轴承的承载能力、刚度、耗气量及摩擦力矩计算如下：

(1)承载能力

轴系径向承载能力为两径向气浮轴承承载能力之和，由于两径向气浮轴承结构完全一致，求解一个气浮轴承的承载能力即可求得所设计轴系的径向承载能力。经计算在不同的偏心率ε，轴承承载能力W如表1所示。

表1 不同偏心率轴承承载能力

Tab.1 Bearing capacity of the beariy withdifferent eccentricity

轴系由两个径向轴承共同支承，有表1可知，在偏心率为0.2的条件下，一个径向轴承承载力为1 539.7N，则轴系的径向承载能力为3 079.4N，实际轴系质量约112.3kg，负载质量要求40kg，则总质量为152.3kg，故轴系承载能力安全系数为2.1，满足设计要求。

(2)刚度

参照(13)式，可计算轴系径向刚度为1 305.2N/μm。

(3)耗气量

径向轴承耗气量由(5)式计算单个节流孔耗气量，乘以总节流孔数可得总耗气量，经计算，径向轴承耗气量为1.6×10-3kg/s，即80L/min。

(4)摩擦力矩

闭式气体静压径向轴承摩擦力矩由下式计算

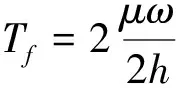
(17)

式中：μ——气体动力粘度系数，一般情况下取μ=17.9×10-6；ω——角速度；h——气膜间隙；D——轴承直径；L——轴承长度。经计算可得，径向摩擦力矩为1.4×10-6Nm，属于极小值，工程上可以忽略不计。

3.3 止推轴承设计

气体静压止推轴承位于两个径向气浮轴承的中间位置，通过对称布置方式，即降低了回转轴系的配平载荷；又使回转轴系结构上更为紧凑，同时还可以起到双向止推提高轴系运转稳定性的作用，止推轴承结构如图8所示。

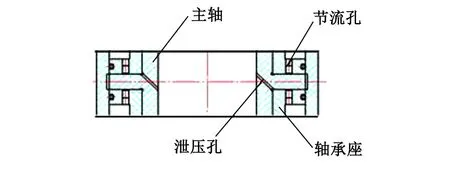
图8 止推轴承示意图Fig.8 Diagram of thrust bearing

止推轴承为小孔节流气体静压止推轴承，轴承内径160mm，外径240mm，节流器节圆直径200mm；节流器数量12个，节流器喉孔直径0.2mm，止推轴承单边气膜间隙10μm。双向止推轴承的承载能力、刚度、耗气量、摩擦力矩等静态特性计算如下：

(1)承载能力

闭式气体静压轴承的承载能力为其所包含的两个开式静压止推轴承的承载能力之差，即

Wb=Ws1-Ws2

(18)

式中：Wb——闭式气体静压轴承承载能力，N；Ws1——一侧止推面承载能力，N；Ws2——另一侧止推面承载能力，N。

经计算，在不同的气膜厚度条件下，止推轴承的承载能力如表2所示。

表2 止推轴承承载能力计算表

Tab.2 Bearing capacity caculation table of thrust bearing

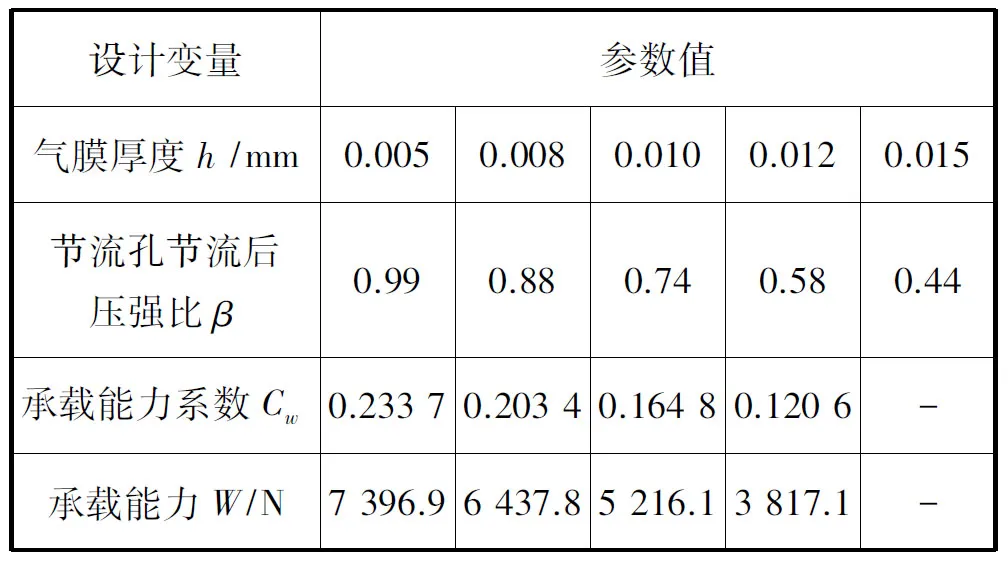
由表2计算结果可知，闭式静压止推轴承在偏心率为0.2时，其承载能力为2 620.7N，即可承载267.4kg，实际回转轴系转子(含负载40kg)质量为152.3kg，止推轴承承载能力安全系数为1.75，满足设计要求。

(2)止推刚度

止推轴承刚度为承载能力对气膜厚度的导数，经式(13)计算可得，止推轴承轴向刚度为1 310.4N/μm。

(3)耗气量

轴向轴承耗气量由(5)式计算单个节流孔耗气量，乘以总节流孔数计算得到总耗气量，经计算，止推轴承耗气量为9.9×10-4kg/s，即49L/min。

(4)摩擦力矩

闭式止推轴承摩擦力矩由下式计算

式中：R1——止推轴承外径；R2——止推轴承内径；经计算止推摩擦力矩为2.7×10-8Nm，属于极小值，工程上可以忽略不计。

4 静压气浮轴系有限元分析

根据所设计气浮轴系参数，以径向静压空气轴承和气体静压止推轴承的气膜为分析对象，为简化计算，分别取1/2气浮轴系气体静压径向轴承和完整气体静压止推轴承，建立静压空气轴承有限元模型并分析计算，网格划分和计算压强分布如图9和图10所示。

(a) 气体静压径向轴承气膜有限元网格模型 (b) 气体静压径向轴承气膜压强分布 图9 气体静压径向轴承气膜有限元分析Fig.9 Finite element analysis of aerostatic pressure radial bearing′s gas film

气体静压轴承气膜压强分布结果如图10所示。

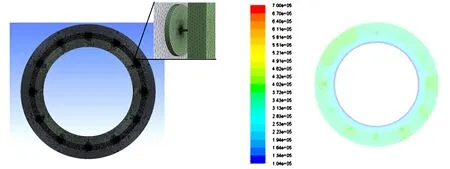
(a) 气体静压止推轴承气膜有限元网格模型 (b) 气体静压止推轴承气膜压强分布 图10 气体静压止推轴承气膜有限元分析Fig.10 Finite element analysis of the aerostatic pressure thrust bearing′s gas film

提取图9(b)和图10(b)各节点压强，通过对工作区域计算，可得轴承径向承载能力为3 800N，止推轴承承载能力为2 806N，有限元分析数值与工程计算数值基本一致，该方法可以用于空气轴承的设计计算。

5 试验验证

按照本文设计参数，实际生产一台气浮轴承，如图11所示。

图11 气体静压轴承实物Fig.11 Physical object of the aerostatic pressure bearing

在气浮轴承台面固定40kg等效负载，利用光电自准直仪对其精度进行测试，气浮轴承在工艺轴上旋转3个位置，每个位置上分别进行顺时针旋转测试和逆时针旋转测试，三个位置分别为轴线垂直，轴线水平，轴线与水平面倾斜45°。平面镜安装在被测轴的轴端，光电自准直仪架设后始终与轴端平面镜准直。测试数据见表3。

表3 静压气浮轴系回转精度测试结果

Tab.3Test results of areostatic pressure shafting rotation precision

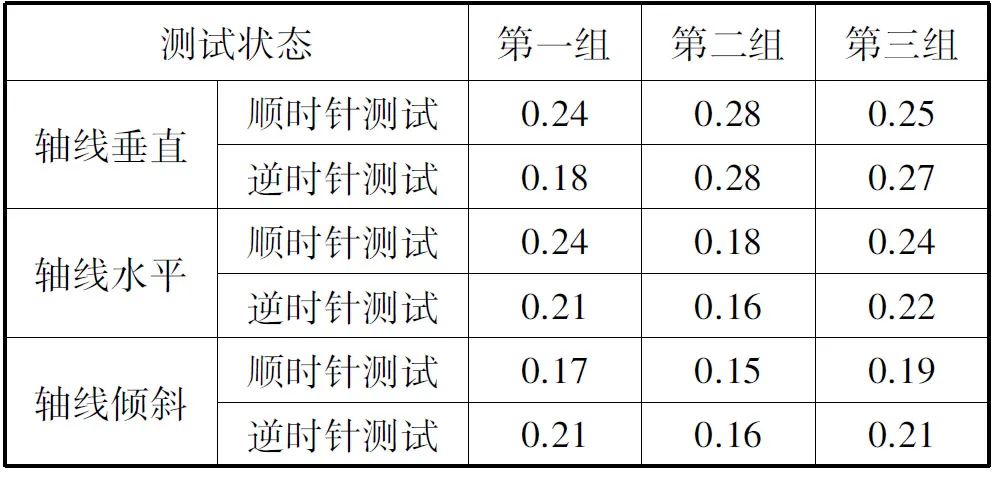
从表3可以看出，在负载40kg的条件下，气浮轴承回转误差在多个测试状态下均小于0.3″，回转精度较高，满足本文负载、回转精度设计要求，也验证了该轴系设计的合理性。

6 结束语

为简化静压气浮轴承计算过程，提高设计效率，本文在满足静压气浮轴承性能的条件下，推导了静压气浮轴承设计的工程计算公式，在此基础上，设计了一款空气轴承结构，确定了几何参数，计算了空气静压径向轴承、空气静压止推轴承的轴承承载力、刚度、耗气量及摩擦力矩，并与有限元仿真结果进行了对比分析，结果表明，计算值与有限元仿真结果基本一致，经试验验证，按本文设计参数加工生产的气浮轴承负载能力、回转精度均满足设计要求，验证了该设计方法的有效性。

[1] 薛景锋,彭军,李新良,赵维谦. 角振动校准装置研究[J]. 航空学报，2015(03)：962～969.

[2] 梁迎春,陈时锦,黄开榜. 惯性系统三轴综合测试转台总体设计若干问题的探讨[J]. 中国惯性技术学报，1996(01)：71～74.

[3] 胡俊宏,孙振鲁,迟青卓,徐良. 静压气浮轴承承载能力的计算机仿真分析[J]. 机床与液压，2014(17)：161～163+127.

[4] 司东宏,张武果,段明德. 基于仿真和正交试验的空气静压径向轴承承载能力研究[J]. 轴承，2013(6)：37～39+42.

[5] 齐乃明,刘暾,李中郢. 三轴精密测试合气浮轴系角刚度数值计算分析[J]. 哈尔滨工业大学学报，1995(3)：70～75.

[6] 张飞虎,付鹏强,汪圣飞,张强. 超精密机床径推一体式空气静压轴承的静态特性(英文)[J]. 光学精密工程，2012(3)：607～615.

[7] 宛敏红.简单孔节流静压气体轴承优化设计的一种解析解法.机械设计与制造，2011(2).

[8] 刘暾，刘育华,陈世杰.静压气体润滑.哈尔滨工业大学出版社，1990.

[9] Dee C W， Shires G L. The current state of the art of fluid bearings with discrete slot inlets[J]. Trans ASME，J Lubric Tech，1971，93(2)：441～450.