测量机器人小视场星图一维最大熵星点图像分割算法
时春霖,张 超,陈长远,杜 兰,叶 凯,韩 忠
1. 信息工程大学,河南 郑州 450001; 2. 上海市空间导航与定位技术重点实验室,上海 200030; 3. 61206部队,北京 100042
视频测量机器人Leica-TS50i全站仪的深度开发,将进一步提高CCD天文定位定向测量的小型化、自动化和数字化。用 CCD 代替传统的照相底片,可获得比照相精度高数倍的星像位置[1]。以CCD数字摄影技术为依托,以不断向智能化发展的全站仪为平台,已成为天文测量的研究和开发方向。CCD 天文定位基本原理是通过CCD相机获取恒星的数字影像,通过数字化可将恒星影像转换为数字信息,利用数字图像处理技术,对恒星数字影像进行坐标量测和数学处理,最终获得测站天文坐标[1]。目前已有基于Leica- TS30(简称TS30)电子经纬仪的天文测量系统及其应用研究[2-4]。2013年徕卡公司推出了新一代的Leica- TS50i(简称TS50i)全站仪[5],作为TS30的替代产品,其在制造工艺和测量功能有了诸多进步,特别是在全站仪中加入了CCD视频拍摄功能,配备视场角为1.5°的长焦相机。相较于一般相机,其采用先进的专业级精密测量镜头,不会产生光学畸变,放大倍数为30×,焦距从1.7 m至无穷远,拍摄星点单一,目标成像达数10像素以上。因此,有必要研究这种基于新型智能平台的天文测量作业模式。
阈值的最佳选取,是图像处理的关键一步。TS50i拍摄星图的阈值分割对星点识别和星点提取至关重要,直接影响到天文定位定向精度。阈值的选取与目标大小、目标和背景的灰度对比度、方差和噪声等因素有关,尚没有一种适合于所有图像的通用的分割算法[6]。常用的阈值分割算法分为全局阈值法和局部阈值法。全局阈值法为整幅图像确定一个阈值,适合前景和背景区分比较明显的图像,特别是适合处理灰度直方图具有明显双峰的图像。其中文献[7]对迭代法[8]具有较好的广谱效应进行了说明,文献[9—10]对Otsu算法[11]应用的广泛性给予了肯定,但是认为其全局阈值法抗噪能力较差。局部阈值法则是根据图像的具体特征,将其划分为若干区域,对每一块进行动态求解阈值,常用的有Bernsen算法[12]、Niblack算法[13]等。局部阈值法往往适用于灰度直方图为多波峰的情况,抗噪能力较强,但是又容易使得局部和细节“过曝”,且处理效率较全局阈值法低。由于传统的全局阈值法和局部阈值法均有可能损失许多信息,对于单峰直方图的图像,上述众多阈值分割算法往往存在效果欠佳的缺点。为了控制信息损失,在图像分割的理论和实践中引入了 “熵”的概念[14-18]。1980 年, 文献[18] 提出了最大后验熵上限法,文献[19]在1982 年采用了图像灰度级的熵进而提出的最小信息互相关法;1985年,文献[20]提出的一维最大熵阈值法获得了广泛应用。
TS50i拍摄图像的灰度直方图呈现明显的“单峰”性。针对TS50i拍摄图像的特点,本文研究探讨了TS50i平台的图像处理方法,通过TS50i对星点进行拍摄,在几种广泛使用阈值分割算法的基础上,对比最大熵的灰度提取法,给出了不同分割阈值下的一维熵的分布图,利用图像的区域一致性和区域对比度原则对分割效果进行了定量分析,验证该算法对处理TS50i星图具有适用性。利用基于一维最大熵的质心提取法对基于真实星空背景的仿真模拟星图进行星点识别和提取,通过和坐标真值进行比对,对该算法的可靠性和准确性进行验证分析。
1 基于一维最大熵的阈值分割算法
1.1 图像灰度特性
灰度直方图是灰度值的函数,它表示图像中具有每种灰度级的像素的个数,反映图像中每种灰度出现的频率。灰度直方图主要分为单峰,双峰和多峰3种类型。图1(a)展示了单峰直方图,它反映了在背景下,目标区域所占比例较小,灰度值相对单一;图1(b)双峰是理想情况,它反映了图像存在两个灰度区域,一个为背景区域,一个为前景区域;而图1(c)多峰直方图是指具有3个及以上波峰的灰度图,它反映出图像内容较复杂,但也最常见。
理想的灰度图像一般认为其灰度直方图具有明显的双峰性。图像中,像素灰度会以较大的概率出现在某些灰度的邻域内,灰度直方图的每个峰值都代表一个目标区域,而谷值则是从一个目标区域到另一个目标区域的过渡点。这样便可以将谷底对应的灰度作为阈值,使得因为阈值选择的误差而导致前景背景错分的影响达到最小,达到最好的分割效果。全局阈值法例如迭代法、Otsu算法都可以达到比较良好的分割效果。
局部阈值法往往适合处理由于光照不均匀、成像质量较差、噪声干扰较大等原因使直方图分布呈现多波峰的图像。实际成像的图像往往受到光照、拍照器件以及噪声等各种因素影响,而呈现多波峰性。多峰直方图也意味着图像内容较为复杂,具有多个子对象。如果成像质量不佳,单纯使用全局阈值法无法兼顾图像各处的实际情况,往往很难取得较好的处理效果。根据图形的实际情况,通常采用适合的局部阈值法进行处理,例如Bersen算法[12]、Niblack算法[13]等。

图1 灰度直方图Fig.1 Gray histogram
单峰直方图往往会出现两种情况。一种是背景和前景灰度分布相差悬殊,造成前景区域在直方图中无法构成明显的波峰;另一种情况是双峰直方图两个波峰相距间隔过于紧密,导致波谷被掩盖而“消失”。由于一种阈值分割算法往往只对某一类或某几类图像有效,且对于具有此类直方图性质的图像目前没有较好的分割方法,往往只能根据具体的图像特点找到特定的阈值分割算法对其进行图像处理。
1.2 一维最大熵法
图像阈值分割就是利用前景和背景之间灰度的特征和差异,通过选择合理的阈值,确定图形中每个像素点属于前景还是属于背景,最后得到处理后的二值化图像。
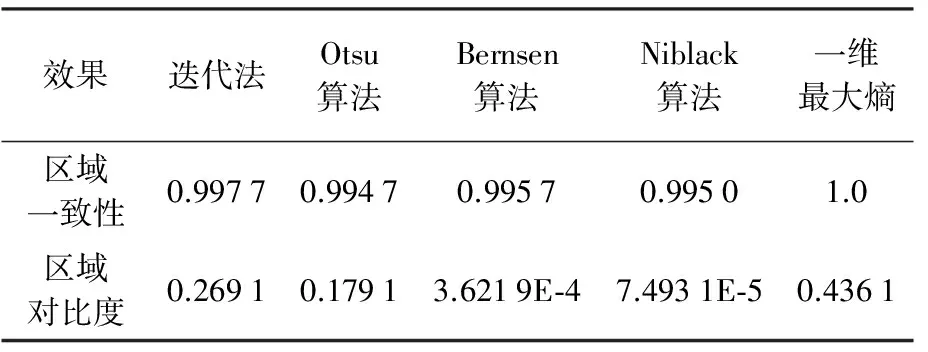
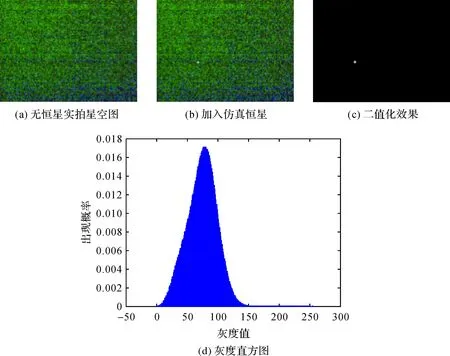
假设原灰度图灰度为f(x,y),以一定的约束条件和准则得到阈值T(0 (1) 显然,阈值的选取是阈值分割的关键。如果阈值选取过低,会导致背景和前景无法区分,背景会被错分为目标;反之,则会造成相反的情况。 图2显示在图像分割的过程中,无论是对于质量好的还是质量差的图像,分割结果均会产生信息的丢失,如采用一般的分割方法,对于质量好的图像可能会产生特征点退化并出现一些伪特征,给后续图像的处理和识别带来很大的困难,而对于质量差的图像则可能会产生大面积的纹线丢失,从而无法识别图像[21]。 图2 图像分割Fig.2 Image segmentation 为了控制此类现象的发生,减少因为图像分割而导致图像信息的损失,人们在图像处理中引入了最大香农熵(Shannon entropy)准则[22]。信息论中,熵是信源的平均不确定度,它是平均信息量的表征,由于信源输出是随机量,因而其不确定度可以用概率分布来进行度量[22]。尽管在原理上基于最大熵的灰度提取法类似于全局阈值法,但是它可以较充分利用图像灰度的信息,尽可能减少图像信息的损失,因此可适用于复杂背景图像的分割,并最早将其称为一维最大熵分割法。一维最大熵分割法的主要思想是:通过引入信息论中最大熵的准则,统计每个灰度级在整幅图像的出现概率,计算每个灰度级的熵,保证各类灰度的总熵最大,由此可以获得使得前景或者背景内部灰度分布尽可能均匀的最优阈值,或是寻找使分割前后图像的信息量差异最小的最优阈值[23]。假设某个灰度级出现概率为P(x),则该灰度级熵的计算公式为[18] H=-P(x)lgP(x)dx (2) 该算法主要实现流程如下: 假设灰度值T(0≤T≤255)为初始阈值,p0、p1、…、pn为图像各个灰度出现概率,前景区域A的灰度pA出现的概率为 pA=p0+p1+p2+…+pT 背景区域B的灰度pB出现的概率为 pB=1-pA=pT+1+pT+2+pT+3+…+pn 此时,将其分为两个概率分布 图像分割后的熵为 遍历整个灰度图,确定合适的阈值T使得H(T)最大,T即为分割阈值。 图3为整个算法的流程图,H(T)最大表示在阈值分割的过程中得到了最大信息的输出,意味前景和背景区域各自的灰度保持最大的统一性,保证了阈值选取的可靠性。该算法抗噪能力较强,对于具有不同信噪比和不同大小目标的图像依然具有较好的分割效果。一维最大熵法在原理上类似于全局阈值法,但是由于该算法对整幅图像计算时涉及对数运算,执行效率较传统的全局阈值法低。 图3 一维最大熵算法流程Fig.3 Flow chart of one-dimensional maximum entropy algorithm 分割效果的评价除了人为主观判断以外,对分割结果进行定性定量分析评价也是必需的。良好的阈值分割应该达到前景与背景清晰分开,并且可以较好地保留目标。通常,用区域一致性和区域对比度[24-27]作为图像分割质量的评价指标。 一个优良的分割效果,应使分割后区域内部元素具有一致性或者相似性,这种特征一致性可以通过计算区域内的特征方差得到[28]。分割后区域内部一致性UM可以表示为[29] (3) 式中,f(x,y)为灰度图的灰度;i通常为1或者2,代表分割后前景区域和背景区域;Ai代表分割区域的像素点个数;C为归一化系数。UM反映了区域内部的均匀性、相似性,UM值越大表示分割区域一致性越强。 区域对比度反映的是分割区域之间的差异性。良好的阈值分割效果使前景和背景应该具有明显差异,即较大对比度。其灰度对比度GC可按照以下公式表示[30] (4) 式中,f1和f2为分割区域的平均灰度。GC数值越大,区域对比度越大,分割效果越好。 首先利用TS50i拍摄实际野外星图图像,与经典肖像图形Lena图进行试验对比,分析各自的灰度特性。其次,分别采用不同阈值分割算法对Lena图和野外拍摄星图进行二值化处理,比较一维最大熵法与常用阈值分割算法的处理结果,利用区域一致性和区域对比度评定图像分割质量。最后,模拟仿真多幅星点分布于不同位置的灰度星图,评定基于一维最大熵法的星点提取算法的准确性和可靠性。 为了进行阈值分割,需预先对TS50i拍摄星图进行去噪和灰度化处理,变成8位灰度图。转化公式如下 gray=0.299R+0.587G+0.114B 式中,gray代表相应灰度(0≤gray≤255);R、G、B为三基色(红、绿、蓝)分量。 图4(见后文)对比了星图和Lena图的原始图像、灰度化后图像和灰度直方图。可以看出: (1) 星图的灰度直方图具有典型的“单峰”性。灰度主要集中在20~130之间,而灰度值较高的星点所占比例很小,是明显的“弱目标”图像。TS50i拍摄星图为24位三通道彩色图像,拍摄视场角小,星点目标单一,图像分辨率达到500万像素(2560×1920像素),图像大小往往为1~2 MB且噪声较大。 (2) Lena图则是典型的多波峰直方图。选取的Lena图也为24位三通道彩色图像,大小为768 kB,像素为512×512,且噪声较小。 图5分别显示了迭代法、Otsu算法、Bernsen算法、Niblack算法和一维最大熵算法对Lena图和TS50i星图灰度图阈值分割后的结果。对比表明: (1) Lena图成像简单、图像质量较高,大多数阈值分割算法均取得良好的二值化结果。其中,传统的全局阈值法(如迭代法和Otsu算法)对于图像整体把握更加协调,且运行效率最快;局部阈值法(如Bernsen算法、Niblack算法)对于细节刻画更加鲜明具体,但是细节处理导致处理时间也较长,效率最低;一维最大熵法在保留整体协调的基础上也较好地保留了细节,尽管处理效率较传统的全局阈值法慢,但是由于拍摄星图的目标星点单一,因而处理效率仍然较高。 (2) 对50幅TS50i拍摄的真实图像进行处理,仅有一维最大熵法具有良好的分割效果,识别图像成功率达到100%。通过一维最大熵法处理后,星图前景与背景分离清晰,分割后目标明显,达到了星点提取的目的。其他阈值分割算法,尽管可以处理单一的目标星点,但是难以处理复杂的星空背景,将星点目标从背景中提取出来。其中,全局阈值法的迭代法和Otsu算法分离出来的星点虽然人眼可以分辨出,但是会呈现大量的噪声点,计算机无法识别分离目标,二值化处理质量不佳。Bernsen算法效果更差,甚至丢失了星点轮廓。Niblack算法则耗时长,效率低,且会出现伪影,无法区分目标星点与大量噪声。 图6给出了不同分割阈值下的熵值分布。从图6可以看出拍摄星图在阈值等于148时熵值最大,与一维最大熵法自适应得到的最佳阈值一致。 图5 几种阈值分割算法的效果对比Fig.5 Comparison of several threshold segmentation algorithms 图6 熵值分布图Fig.6 Entropy distribution 表1显示了以上几种算法处理星图时的区域一致性和区域对比度。显然,通过一维最大熵得到的区域一致性和区域对比度同时最高,与人眼观测结果基本一致,表明一维最大熵法对星图分割的良好处理效果。 表1星图阈值分割算法效果评价 Tab.1EffectEvaluationofstarimagethresholdsegmentationalgorithms 效果迭代法Otsu算法Bernsen算法Niblack算法一维最大熵区域一致性0.99770.99470.99570.99501.0区域对比度0.26910.17913.6219E⁃47.4931E⁃50.4361 野外天文测量的经纬度精度指标决定了TS50i图像星点提取的像素精度要求。TS50i图像分辨率为2560×1920像素,视场角为1.5°,根据式(5),可以计算出单像素对应的角秒,即 (5) 式中,A为视场角;X、Y分别为图像的横纵向分辨率。因此,TS50i拍摄的星图1像素对应约1.7″。 表2列出了基于TS50i野外天文测量的像素精度指标。一等天文经纬度精度要求是0.3″,对应到TS50i拍摄星图精度要求约为0.18像素,野外二等天文测量经纬度精度要求分别为0.6″和0.5″,对应到TS50i拍摄星图精度要求分别约为0.36像素和0.30像素。 需要说明的是,根据误差传播定律和协方差分析,在没有其他误差源的影响下,量点提取的误差对最终实际解算的定位结果影响将缩减到原值的1/6左右。 表2 野外天文测量精度指标 由于TS50i真实拍摄星图无法得到星点的像素坐标真值,这里采用实际拍摄无恒星目标的星空图像+人工仿真的已知星点,共计仿真120幅星图图像。通过大量的野外观测发现,恒星星点像素通常为数十到数百像素,即使在城市夜景下,四等恒星的像素数也达近100像素。现采用像素数为400且具有灰度梯度的白色圆作为模拟星点,其灰度分布为 (6) 式中,(i,j) 为模拟星点内的像素坐标;(x,y)为模拟星点圆心坐标;g(i,j)为模拟星点的灰度;k为比例系数。模拟星点各像素距离圆心距离越远,灰度值越小。 图7给出了具体的仿真星图: 图7(a)显示了真实拍摄无恒星目标的星空图像,图7(b)显示了在真实拍摄无恒星目标的星空图像下加入仿真星点后的图像,图7(c)显示了对图7(b)一维最大熵处理后的二值化效果,图7(d)显示了图7(b)灰度图像的灰度直方图,与野外实际拍摄星图的灰度直方图一致,为典型的灰度单峰图。 表3和图8给出了算法提取的星点坐标与真实坐标的比较。120幅星图的统计结果表明,星点的提取精度较野外一等天文测量精度要求高一个数量级。其中x轴方向RMSE为0.015像素,y轴方向RMSE为0.017像素,证明基于该算法进行星点提取精度可靠,RMSE为均方根误差,用来衡量像点提取坐标与设置的真值之间的误差。图7显示了x、y轴均方根的分布,表3给出了其中4幅图像星点提取像素坐标与星点模拟坐标值及误差统计结果。 表3部分模拟星图星点提取坐标 Tab.3Thestarextractionofpartofthesimulationmapcoordinates 像素 图4 原始图像、灰度图及其灰度直方图Fig.4 Original images,the gray images and gray histograms 图7 仿真星图Fig.7 Simulated sky images 图8 均方根分布图Fig.8 Distribution of root mean square 面向基于视频测量机器人TS50i的自动天文测量系统开发,提出了运用一维最大熵法处理TS50i拍摄的星图图像。根据星图的小视场、单星点、弱目标和单峰性的特点,对比了几种常用的阈值分割算法,给出不同分割阈值下的熵值分布,采用了对实际星点拍摄的照片,并根据基于大量实拍星图背景的模拟仿真数据,得到天文测量和提取星点坐标的像素精度。试验表明: (1) 对于成像简单、质量较高的图像,传统的阈值分割算法大都取得良好的二值化结果。对于实际拍摄星图,传统的阈值分割算法尽管可以处理单一的目标星点,但是难以处理复杂的星空背景,将星点目标从背景中提取出来。 (2) TS50i拍摄的星图,通过灰度化处理后,得到的灰度直方图具有明显的“单峰”特征。在处理星图时,一维最大熵法可以自适应获得最佳分割阈值,图像处理效果优于迭代法、Otsu算法、Bernsen算法、Niblack算法等阈值分割算法,对拍摄星图具有良好的适用性,且由于其目标星点单一,算法处理效率较快。 (3) 通过仿真120幅灰度星图,利用基于最大熵法的星点提取算法对仿真模拟星图进行处理,星点提取精度较野外一等天文测量精度要求高一个数量级。提取坐标与星点坐标真值相比,x轴方向均方差为0.015像素,y轴方向均方差为0.017像素,试验证明算法准确可靠,可以满足野外高精度天文测量需要。 值得说明的是,一维最大熵法不仅在处理TS50i小视场、单星点、弱目标和单峰性的星图时效果良好,在处理某些传统相机拍摄的多星点星空图像时仍能获得优良的二值化效果,对处理基于其他平台拍摄的星图具有借鉴意义。 参考文献: [1] 郭敏, 张红英. CCD数字摄影在天文定位测量中的应用探讨[J]. 测绘技术装备, 2005, 7(1): 28-29. GUO Min, ZHANG Hongying. Discussion of CCD Digital Photography Applying on Chronometer Orientation Survey[J]. Geomatics Technology and Equipment, 2005, 7(1): 28-29. [2] Leica Geosystems. Leica TS30/TM30 User Manual[M].Heerbrugg,Switzerland:Leica Geosystems,2000. [3] 张超. 基于电子经纬仪的天文测量系统及应用研究[D]. 郑州: 信息工程大学, 2009. ZHANG Chao. System-level Development and Application Research on Astronomic Surveying System Based on Electronic Theodolites[D]. Zhengzhou: Information Engineering University, 2009. [4] 宋飞杰, 张超, 王若璞, 等. Leica-TS30在天文测量中的应用[J]. 测绘科学技术学报, 2015, 32(2): 135-139. SONG Feijie, ZHANG Chao, WANG Ruopu, et al. Application of Leica-TS30 on Astronomic Surveying System[J]. Journal of Geomatics Science and Technology, 2015, 32(2): 135-139. [5] Leica Geosystems. Leica MS50/TS50/TM50 User Manual[M].Heerbrugg,Switzerland:Leica Geosystems,2000. [6] 陈冬岚, 刘京南, 余玲玲. 几种图像分割阈值选取方法的比较与研究[J]. 机械制造与自动化, 2003(1): 77-80. CHEN Donglan, LIU Jingnan, YU Lingling. Comparison of Image Segmentation Thresholding Method[J]. Jiangsu Machine Building & Automation, 2003(1): 77-80. [7] 童立靖, 张艳, 舒巍, 等. 几种文本图像二值化方法的对比分析[J]. 北方工业大学学报, 2011, 23(1): 25-33. TONG Lijing, ZHANG Yan, SHU Wei, et al. Comparison and Analysis of Several Document Image Binarization Algorithms[J]. Journal of North China University of Technology, 2011, 23(1): 25-33. [8] RIDLER T W, CALVARD S. Picture Thresholding Using An Iterative Selection Method[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1978, 8(8): 630-632. [9] 江明, 刘辉, 黄欢. 图像二值化技术的研究[J]. 软件导刊, 2009, 8(4): 175-177. JIANG Ming, LIU Hui, HUANG Huan. The Research of Image Binarization Technology[J]. Software Guide, 2009, 8(4): 175-177. [10] 谭凯, 张永军, 童心, 等. 国产高分辨率遥感卫星影像自动云检测[J]. 测绘学报, 2016, 45(5): 581-591. DOI: 10.11947/j.AGCS.2016.20150500. TAN Kai, ZHANG Yongjun, TONG Xin, et al. Automatic Cloud Detection for Chinese High Resolution Remote Sensing Satellite Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 581-591. DOI: 10.11947/j.AGCS.2016.20150500. [11] OSTU N. A Threshold Selection Method from Gray-level Histograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62-66. [12] BERNSEN J. Dynamic Thresholding of Grey-level Images[C]∥Proceedings of the 8th International Conference on Pattern Recognition. Paris, France: IEEE, 1986. [13] NIBLACK W. An Introduction to Digital Image Processing[M]. New Jersey: Prentice Hall, 1986: 115-116. [14] SHIOZAKI A. Edge Extraction Using Entropy Operator[J]. Computer Vision, Graphics, and Image Processing, 1986, 36(1): 1-9. [15] PAL N R, PAL S K. Object-Background Segmentation Using New Definitions of Entropy[J]. IEE Proceedings: E-computers and Digital Techniques, 1989, 136(4): 284-295. [16] LEE S S, HORNG S J, TSAI H R. Entropy Thresholding and Its Parallel Algorithm on the Reconfigurable Array of Processors with Wider Bus Networks[J]. IEEE Transactions on Image Processing, 1999, 8(9): 1229-1242. [17] PAL N R, PAL S K. Entropy: A New Definition and Its Applications[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1991, 21(5): 1260-1270. [18] PUN T. A New Method for Grey-level Picture Thresholding Using the Entropy of the Histogram[J]. Signal Processing, 1980, 2(3): 223-237. [19] JOHANNSEN G, BILLE J. A Threshold Selection Method Using Information Measures[C]∥Proceedings of the 6th International Conference on Pattern Recognition. Munich, Germany: IEEE, 1982: 140-142. [20] KAPUR J N, SAHOO P K, WONG A K C. A New Method for Gray-level Picture Thresholding Using the Entropy of the Histogram[J]. Computer Vision, Graphics, and Image Processing, 1985, 29(3): 273-285. [21] 田俊霞, 穆国燕, 陈树中. 基于边界特征的一维最大熵图像分割算法的研究与实现[J]. 计算机工程与科学, 2002, 24(6): 46-47, 64. TIAN Junxia, MU Guoyan, CHEN Shuzhong. Research and Implemention of One-dimensional Maximum-entropy Threshold Image Segmentation Based on Edge Features[J]. Computer Engineering and Science, 2002, 24(6): 46-47, 64. [22] WONG A K C, SAHOO P K. A Gray-level Threshold Selection Method Based on Maximum Entropy Principle[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1989, 19(4): 866-871. [23] 黄春艳, 杨国胜, 侯艳丽. 基于熵的图像二值化方法比较研究[J]. 河南大学学报(自然科学版), 2005, 35(2): 76-78. HUANG Chunyan, YANG Guosheng, HOU Yanli. Comparison Research on Image Binarization Algorithms Based on Entropy[J]. Journal of Henan University (Natural Science), 2005, 35(2): 76-78. [24] 李敏强, 寇纪淞, 林丹, 等. 遗传算法的基本理论与应用[M]. 北京: 科学出版社, 2002: 163-208. LI Minqiang, KOU Jisong, LIN Dan, et al. Basic Theory and Application of Genetic Algorithms[M]. Beijing: Science Press, 2002: 163-208. [25] 侯格贤, 毕笃彦, 吴成柯. 图像分割质量评价方法研究[J]. 中国图象图形学报, 2000, 5(1): 39-43. HOU Gexian, BI Duyan, WU Chengke. Researches on Evaluation Methods for Image Segmentation[J]. Journal of Image and Graphics, 2000, 5(1): 39-43. [26] 章毓晋. 图像分割评价技术分类和比较[J]. 中国图象图形学报, 1996, 1(2): 151-158. ZHANG Yujin. A Classification and Comparison of Evaluation Techniques for Image Segmentation[J]. Journal of Image and Graphics, 1996, 1(2): 151-158. [27] 汪荣贵, 吴昊, 方帅, 等. 一种新的自适应二维Otsu图像分割算法研究[J]. 中国科学技术大学学报, 2010, 40(8): 841-847. WANG Ronggui, WU Hao, FANG Shuai, et al. A New Adaptive Two-dimensional Otsu Image Segmentation Algorithm Research[J]. Journal of University of Science and Technology of China, 2010, 40(8): 841-847. [28] 王润生. 图像理解[M]. 长沙: 国防科技大学出版社, 1995: 113-117. WANG Runsheng. Image Understanding[M]. Changsha: National University of Defense Technology Press, 1995: 113-117. [29] SAHOO P K, SOLTANI S, WONG A K C, et al. A Survey of Thresholding Techniques[J]. Computer Vision, Graphics, and Image Processing, 1988, 41(2): 233-260. [30] LEVINE M D, NAZIF A M. Dynamic Measurement of Computer Generated Image Segmentations[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1985, 7(2): 155-164.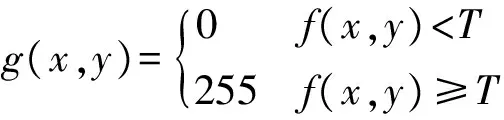


1.3 分割效果评价
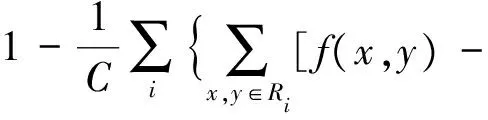
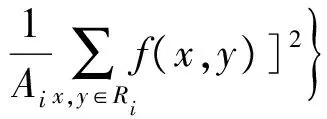
2 试验结果与分析
2.1 星图的灰度直方图特点
2.2 星图的阈值分割效果


2.3 星点提取精度




3 结 论

