基础沉降计算的数值积分算法
许德胜
(上海同豪土木工程咨询有限公司,上海市 200092)
0 引言
基础在承受上部结构荷载后会发生沉降,基础的沉降必然会引起上部结构下沉,从而影响结构的正常使用。基础沉降对超静定结构还会引起结构的附加内力,影响结构的安全性[1]。
基础沉降的计算方法主要有以下三类:弹性力学方法、分层总和法和地基规范法[2,3]。弹性力学方法基于均质半空间假设的Boussinesq位移解进行计算,由于实际地基为非均质成层土,导致该方法得到的基础沉降量比实际沉降量偏大。分层总和法把地基土视为线性变形体,假定外载作用下的地基变形仅发生在有限厚度的压缩层,通过将压缩层分层并求解各层附加应力,利用土的侧限压缩曲线分别求得各层的压缩量,并将分层的压缩量求和计算基础的最终沉降。分层总和法通常可得到比弹性力学方法更接近实际的解答,但为保证计算精度,对土层的分层厚度有严格要求,计算工作量较大[4]。地基规范法是目前《建筑地基基础规范》推荐的计算方法[5],是对分层总和法的改进和简化,通过采用平均附加应力系数计算基础沉降量,该方法与实际情况吻合较好。现行规范给出了矩形基础的平均附加应力系数表格,对任意形状基础的沉降计算需采用角点法,简化为相应矩形基础才能计算,对基础荷载的分布情况在使用上也存在限制。
本文基于Boussinesq应力解答,通过将基础所在区域做网格离散,利用二维高斯数值积分计算各土层的附加应力。其后,沿土层厚度方向对所得附加应力做一维高斯数值积分,可直接计算基础沉降量,无需平均附加应力系数的计算。文中方法本质上为规范基础沉降计算方法的数值实现,但该算法可适用于任意的基础形式,可精确考虑任意荷载分布,更便于计算机程序的实现。
1 土层附加应力计算
图1所示弹性半空间表面作用竖向集中力P时,半空间内任意点处竖向附加应力的弹性力学解答可由Boussinesq解答得到[3],

图1 集中力P作用下的弹性半空间中任意点M
对任意分布荷载p(x,y),在任意点M处竖向附加应力可通过积分表达为:
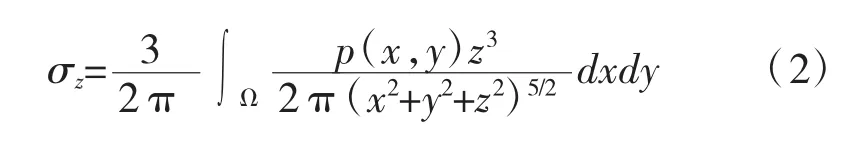
其中,Ω为荷载的分布区域,若要考虑相邻基础或台背路基填土等其他荷载的影响,则这些区域也应计入该积分域。
本文采用高斯数值积分方法计算(2)式表达的附加应力。为此,将求解域Ω离散为若干四边形单元,三角形单元可视为具有共节点的四边形单元的退化形式,见图2。若存在相邻基础或其他临近荷载,则相邻基础或附加荷载所在区域同样要做网格划分。网格离散后引入有限单元法中平面四节点等参元的等参变换[6,7]。
其中,Nk=(1+ζkζ)(1+ηkη),k=1~4 为四节点等参单元的插值形函数,对单元域内任意点的荷载集度p(x,y)可采用相同的插值函数进行插值。
此时,任意空间点M处的附加应力可按式(4)进行计算:
式中:ne为划分的单元数;nx和ny为单元内沿x向和y向布置的高斯点数;wj和wk为求积系数;f(ξj,ηk)为式(2)中在积分点位置的被积函数;J1为式(3)坐标变换所定义的雅可比矩阵。利用式(4)即可计算得到任意分布的基底压力p(x,y)作用下,在不同位置处的附加应力值。
2 基础沉降计算
《建筑地基基础设计规范》给出的基础沉降量计算公式为[5]:

式中:s为地基最终沉降量;ψs为沉降计算经验系数,可由当量压缩模量确定;n为地基沉降计算深度范围内的土层数;p0为准永久组合时的基底压力分布;Esi为第i层土压缩模量,可由土的压缩曲线得到;zi和zi-1为基础底面至第i层土和第i-1层土底面的距离;αi和αi-1为基础底面至第i层土和第i-1层土底面范围内的平均附加应力系数。
根据平均附加应力系数的定义[3,8],式(5)可表达为下述积分形式:
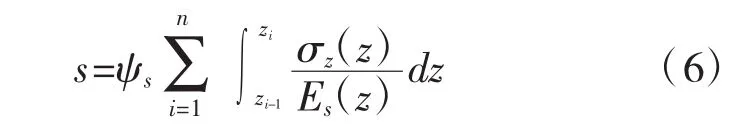
对任意给定的基础沉降计算点S(x,y),其下任意深度z处的附加应力σz(z)可由式(4)进行计算,而任意深度z处的压缩模量Es(z)可直接由土的侧限压缩曲线得到,为准确计算积分点位置的压缩模量,本文采用了文献[9]中的非线性拟合方法。
为计算式(6),引入一维等参变换[6,7],

其中,插值形函数 Nj=(1+ζjζ)/2;不难看出,该插值形函数与两节点杆单元的形函数完全相同。式(6)的积分同样可用高斯积分表达为:
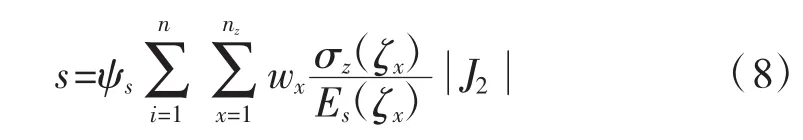
其中,J2为式(7)坐标变换定义的的雅可比矩阵。需要指出,上式中沉降计算经验系数ψs需采用压缩模量当量值查规范表格得到,而当量压缩模量的计算表达式同样可通过高斯积分计算,过程与式(8)的推导类似,不再赘述。
3 程序实现流程
为考核本文计算方法的有效性,按图3所示流程编制了相应的计算程序。需要指出,在深度方向仅设置一个高斯积分点时,本文方法可直接退化为规范给出的计算方法,即使对厚度比较大的土层也无需对土层进行细分,只需按照土层的天然分层性,沿深度方向适当提高积分点数即可获得满意的计算精度。本文在分析时在平面和深度方向均采用了两点高斯积分进行计算。
4 算例
基础沉降量的计算依赖于其下卧层附加应力的确定,附加应力的计算能否适应任意的基础形状以及任意分布的荷载情况是本文基础沉降算法具有广泛适应性的前提。为考察本文方法的适用性及计算效率,选取相关文献中的若干算例[2,3]进行计算,并与参考解进行比较。
4.1 圆形基础附加应力分析
考察半径为2 m的圆形基础,其上作用中心荷载Q=150 kN,计算基础边缘下的竖向附加应力分布。采用本文方法计算时共划分了360个单元,表1给出了采用不同高斯积分点数时附加应力σz的分布。本例用于考察本文方法对任意形状基础的适用性以及算法的收敛性。

图3 基础沉降计算流程

表1 圆形基础边缘点附加应力分布 kPa
4.2 三角形分布荷载下的附加应力分析
图4所示尺寸为5 m×3 m的矩形基础上作用三角形分布荷载,荷载最大值p=100 kPa,计算在矩形面积内o点下深度z=3 m处M点的竖向应力σz值。本例用于考察本文算法对任意分布荷载的适用性。

图4 三角形分布荷载作用下的矩形基础
为计算M点的附加应力,文献[2]中进行了两次叠加计算:第一次是荷载作用面积的叠加,将基础转换为4个矩形计算域;第二次是荷载分布图形的叠加,将三角分布荷载转换为1个均匀分布的荷载和2个三角形荷载,计算过程相当繁琐,且不便于编制程序利用计算机求解。本文计算时,仅需将基础离散为16个三角形单元即可。计算结果见表2,可见本文算法具有较高的计算精度。

表2 三角分布荷载下M点附加应力计算结果 kPa
4.3 条形基础梯形荷载下的附加应力分析

图5 路堤填土引起的附加应力
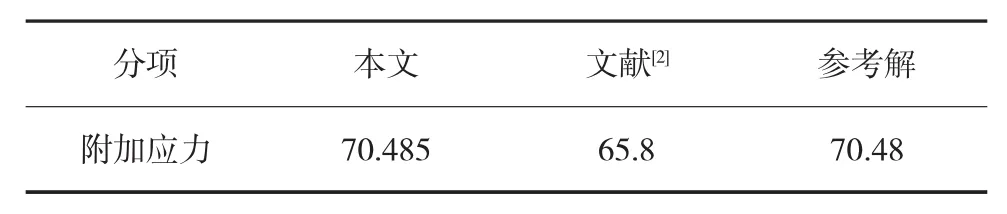
表3 条形基础下M点附加应力计算结果 kPa
需要指出,采用本文方法计算时建立了长为200 m宽为20 m的矩形基础模拟图5中的条形基础。表3所列参考解基于《建筑地基基础设计规范》中附录K计算得到。
4.4 考虑相邻基础影响的基础沉降量分析
为考察相邻基础的影响,计算图6中基础甲的沉降量,并考虑两侧相邻基础乙的影响。作用于各基础的外荷载均为1 940 kN,地下水位标高-3.5m,基础底面标高-1.5 m。土层压缩曲线见文献[3],土层的其他地质参数列于表4。
表5给出了计算深度范围内的附加应力计算结果,计算时三个基础共划分了479个三角形单元。不难看出,本文方法有较高的计算精度。

图6 基础几何尺寸

表4 土层地质参数
表6给出了基础甲中心点位置处沉降量的计算值及压缩模量当量值。需要指出,本例沉降计算时,本文采用了土层的天然分层,文献中的参考解采用2 m层厚进行分层计算得到。
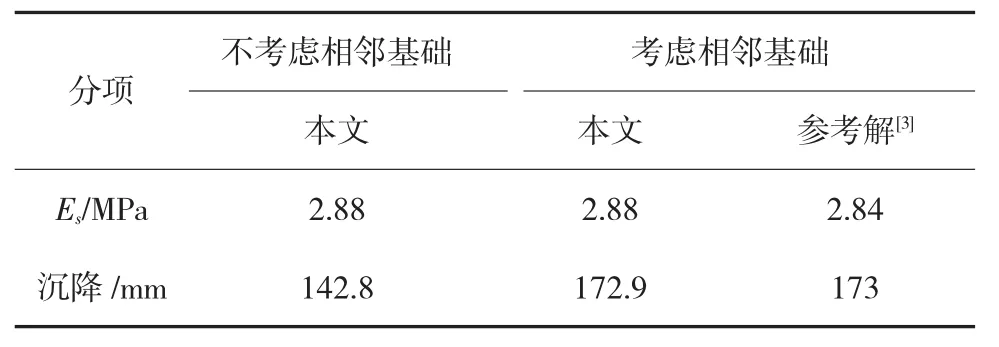
表6 基础沉降量及压缩模量当量值
5 结论
(1)本文基于Boussinesq应力解,引入四节点单元的等参变换,采用数值积分的方法计算土层附加应力,可适应任意基础形式和任意基底压力分布的复杂情况,对考虑相邻基础的影响也十分简便。
(2)通过直接对附加应力沿土层厚度方向进行数值积分,避免了平均附加应力系数的计算,增加沿厚度方向的积分点数,可避免对厚度较大的土层做细分。
(3)算例表明本文方法具有较高的计算精度,易于计算机编程实现,便于在工程中应用。
参考文献:
[1]JTG D63-2007,公路桥涵地基与基础设计规范[S].
[2]高大钊.土力学与基础工程[M].北京:中国建筑工业出版社,1998.
[3]华南理工大学,等.地基及基础[M].北京:中国建筑工业出版社,1991.
[4]徐金明,汤永净.分层总和法计算沉降的几点改进[J].岩土力学,2003,24(8):518-521.
[5]GB 50007-2011,建筑地基基础设计规范[S].
[6]Zenkiewicz O C,Taylor R L.The finite element method [M].McGraw-Hill,New York,2005.
[7]王勖成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,1997.
[8]赵明华,李刚,曹喜仁,等.土力学地基与基础疑难释义[M].北 京:中国建筑工业出版社,2003.
[9]杜秀忠,杨光华.软土e-p曲线的分析、拟合及应用[J].广东水利水电,2005(6):20-23.

