扶壁式闸墙沉降及倾斜研究

许瑞东

（上海嘉定水务工程设计有限公司，上海市 201800）

0 引言

船闸的闸室结构主要有斜坡式和直立式两种，斜坡式闸室由于使用不方便，且耗水量大，目前已很少采用。直立式闸室按其受力状态分为整体式和分离式结构两大类，一般情况下采用分离式闸室结构比较经济合理，且扶壁式为工程实践中最常用的结构型式。扶壁式闸室在运转过程中，在地质、荷载、回填土、闸室水头等综合因素影响下，闸室产生倾斜变形，情况轻微的只是改变闸室的有效高度，不会对船闸整体及通航产生影响；变形严重的危及船闸的通航能力和安全运行，国内鲜有学者研究扶壁式闸室的倾斜，影响闸室倾斜的因素主要为地基土的不均匀沉降，扶壁式底板及立板自身变形，及闸室水位引起的墙身倾斜[1]。对于扶壁式闸室的沉降计算主要按照船闸水工建筑物设计规范[2]提供的式（1）计算。

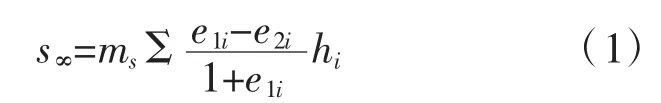
式中：s∞为地基土最终沉降量，m；ms为经验修正系数，按地区经验选用；e1i、e2i分别为第i层土受平均自重压力（σci）和平均最终压力（σci+σsi）压缩稳定时的孔隙比；σci为第i层顶面与底面的地基自重压力的平均值，kP a；σsi为第i层顶面与底面的地基垂直附加应力平均值，kP a；hi为第i层土体的厚度，m。

不包括软土的粘性土地基，当基底压力小于或接近于船闸闸基未开挖前作用于该基底面上土的自重压力时，土的压缩曲线宜采用e-p回弹再压缩曲线;软土地基土的压缩曲线宜采用e-p曲线;大型船闸工程，土的压缩曲线宜采用e-lgp曲线。

该规范考虑到砂性土、粘性土地基固结的不同特点，为安全计，从可能的最不利情况出发，边载采用两个极限值，但规定的取值范围大，实际计算时较难把握。对于固结计算常用的太沙基理论[3]假设法向总应力和不随时间变化，因此只适应于一维固结，对于三维复杂情况则准确性较差。另外，基坑开挖后，地基土应力不会立即得到释放，基底回弹不会马上完成，原地面以下、以上填土的边荷载效应存在差异，这些问题对船闸结构位移、变形、内力的影响尚未得到充分考虑[4]。因此，开展闸室沉降变形及倾斜研究，对合理确定闸室预留沉降和预倾量以满足规范要求[5]，提高闸室墙倾斜预测水平具有重要的理论意义和实用价值。

本文通过利用Abaqus有限元软件采用Bi ot固结理论与能较好模拟土体非线性特征及回弹在压缩特征的修正剑桥模型[6-7]对邵伯三线船闸的现有地形、地质条件、结构型式以及墙后回填土等进行模拟，考虑基坑开挖回弹在压缩、地基土的渗流固结、回填土与闸室墙的接触以及闸室水头因素的影响，并与现场实测资料进行比较分析研究各期扶壁式闸室的结构的沉降变形及倾斜变形，分析其机理，其研究结果可为类似工程提供参考。

1 理论介绍

1.1 biot固结理论[8]

在荷载作用下，水从土体孔隙中挤出，土体收缩的固结过程，是一种流体-固体的相互作用（流固耦合）。比奥（Riot）从固结机理出发，较严格地推导了孔隙压力消散与土骨架变形相互关系的三维固结平衡方程及连续性方程。

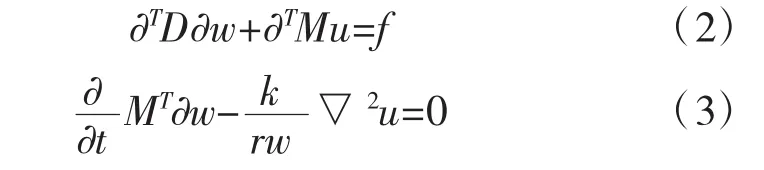
式中：∂为偏微分算子；▽2为拉普拉斯算子;w为位移分量w=[wx，wy，wz];u为超静孔隙压力;D为弹塑性矩阵;M为单位矩阵;k为土的渗透系数;rw为水体重度f为外荷载列阵。

Bi ot固结理论可以很好模拟固结过程中位移与孔隙压力的相互影响，反应二者的耦合。

1.2 修正剑桥模型

修正剑桥模型从理论上和试验上都较好地阐明了土体的弹塑性变形特性，是应用最为广泛的软土本构模型之一

模型假定在排水条件下，当软土试样在各向等压（σ1′=σ2′=σ3′=p′）作用下慢慢压缩时，比体积 v和ln p′形成一条直线（正常固结线），见图1；当卸载时试样发生回弹，v和ln p′形成回弹曲线。

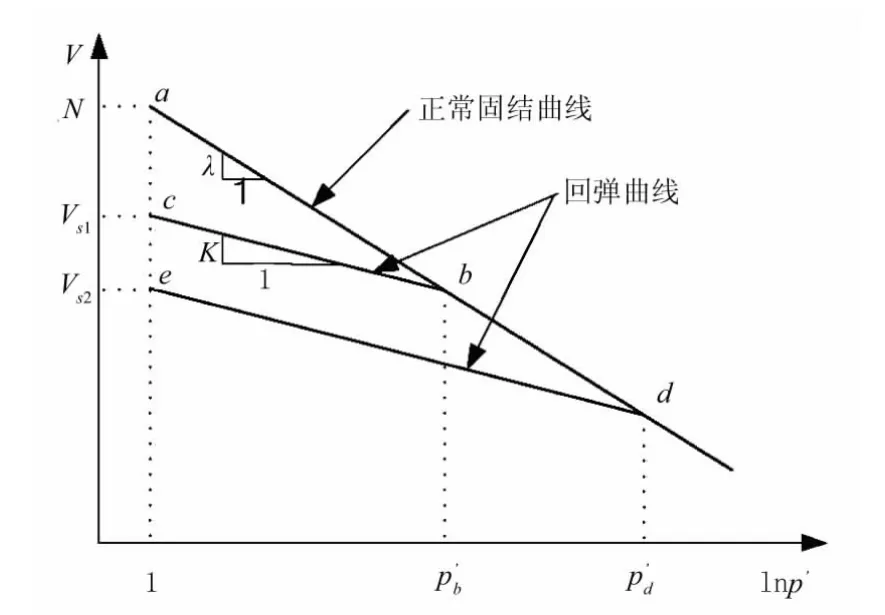
图1 土样在各向等压下的行为

其屈服面函数[9]由式（4）表示

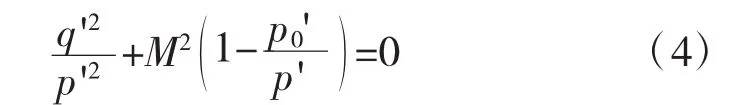
在p′-q′面上，修正剑桥模型的屈服面为椭圆。参数p0′为先期固结压力，它控制了屈服面的大小。参数M为p′-q′面上临界状态线的斜率，见图2。

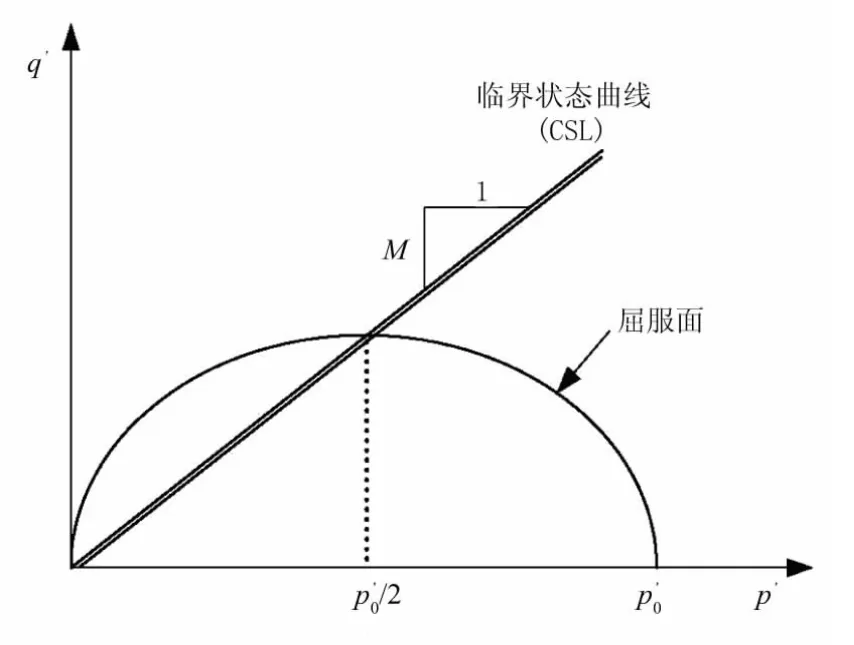
图2 修正p′-q′剑桥模型在面上的屈服面

硬化和软化行为如果屈服发生在临界状态线与屈服面交点的右边，则伴随着压缩硬化过程，土样骨架为了抵抗压力而被压缩，当试样受剪时，开始表现出弹性变形行为，直至达到初始屈服面，之后屈服面开始增大并表现出硬化状态。如果屈服发生在临界状态线与屈服面交点的左边，则伴随着膨胀的软化过程，在软化中，当应力状态达到初始屈服面时，屈服面开始缩小，屈服面和维持荷载不断减小，直到试样达到临界状态。

2 工程实例

2.1 邵伯三线船闸概况

邵伯三线船闸位于二线船闸的西侧，邵伯船闸闸室为扶壁式结构，净宽23.0 m，闸室墙底板厚0.9 m，宽为12.5 m，立板厚0.6 m，高11.9 m，肋板厚0.5 m。底板采用透水底板和钢筋混凝土纵横格梁。原地面高程6.3 m，闸室墙顶高程为▽10.23 m，原地下水位高程▽4.5 m。

2.2 有限元模型

本文依照实际工程原尺寸建立闸室有限元模型（见图3、图4），由于闸室模型几何形状及受力条件具有对称性，为简化计算量本文在闸室横向建立一半右岸闸室模型，在纵向建立半个扶壁段。闸室后方取46 m范围内土体，闸室墙底下方取22.5 m范围内土体，以闸室侧为x正方向。利用单元生死功能[10]来模拟土体的开挖回填。在土体及结构之间设置接触，摩擦系数取为0.268，法向接触设为硬接触。模型底部采用固定约束，四周侧面采用法向约束。扶壁墙及底板采用弹性模型，本文地基土体采用修正剑桥模型，各参数由式（5）求出，其中λ、κ可根据固结试验由式（5）求得[11]。

式中：Cc、Cs为土在e-lnp平面的压缩指数、回弹指数。许多学者对λ和κ之间的关系进行了统计，λ/κ一般介于5～10，本文分析时取λ/κ，即根据λ来确定κ。

图3 整体有限元模型

图4 回填前有限元模型

M可根据三轴压缩试验由式（6）得到[11]

式中：φ′为三轴试验得到的有效内摩擦角。

考虑到本工程闸墙顶高程高出原地面▽6.3～10.23 m不多，回填土的变形对地基变形影响有限，因此回填土体采用摩尔-库仑模型。原土基及回填土初始孔隙比为0.74，渗流系数取为2e-9m/s。各材料参数见表1及表2。

表1 扶壁墙、底板及回填土材料参数

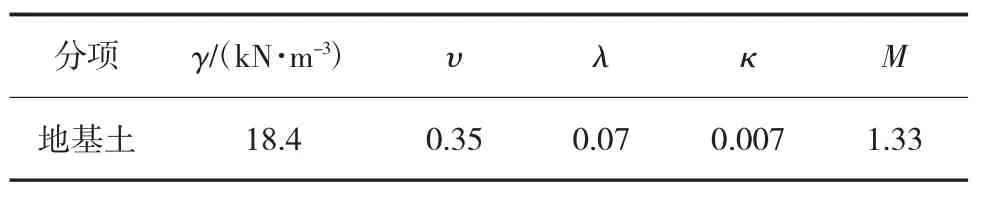
图2修正剑桥模型在面上的屈服面

2.3 计算工况

本文模拟了以下几种施工次序：基坑一次开挖（2个月）→渗流固结计算10个月→浇筑闸墙（10个月）→浇筑底板（1个月）→回填土填筑（6个月）→固结计算2个月→闸室蓄水水位6 m时的固结6个月→闸室蓄水水位4.8 m时的固结10个月。位移-时间曲线以闸室开始浇筑为时间零点，共三年零八个月。原地下水位▽4.50 m，地下水位以上土体采用湿重度，地下水位以下采用浮重度，后期蓄水后地下水位取为排水孔高程▽3.3 m。为分析闸室灌泄水过程中闸墙前、后趾地基反力变化及闸室墙体位移变化，本文在前面分析过程基础上计算了灌泄水过程对闸室变形影响。计算工况为闸室水位▽4.8 m，地下水位高程▽3.3 m，水头差1.5 m。

3 结果分析

3.1 施工期墙身倾斜及沉降结果

图5为前、后趾沉降有限元结果及实测结果，图6为前后趾沉降差值有限元结果与实测结果。在基坑开挖后前趾回弹59.6 mm，后趾回弹53.8 mm，前后趾均有较大回弹且前趾回弹量大于后趾，但二者差异较小。

图5 地基沉降-时间曲线

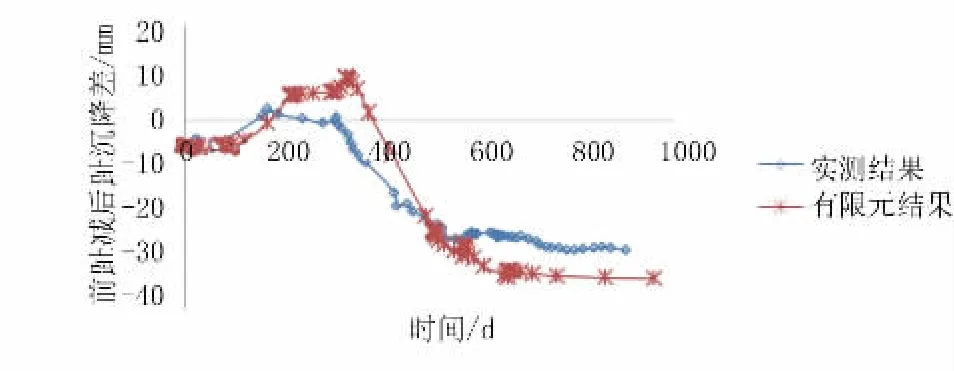
图6 前后趾地基沉降差值

从扶壁式闸墙浇筑开始，由图可以看出在闸墙底板浇筑后地基土开始下沉且前趾沉降与后趾成降的差值主要为前后趾回弹量不同引起的，在立板浇筑后由于闸室墙重心偏向前趾所以前趾沉降大于后趾沉降但差值较小在10 mm之内，此时闸墙向闸室方向倾斜。由于有限元模型未能准确的模拟闸墙浇筑过程中复杂的施工环境等，在此阶段有限元结果沉降差值大于实测资料，但基本变化趋势是一致的。

在回填土回填阶段由于回填土作用在闸室底板上的重力及其在底板外的边载作用下，有限元结果及实测结果均显示出在回填初期后趾沉降开始大于前趾沉降，在此阶段前后趾沉降速率较快，闸室墙由向闸室方向倾斜变为向填土方向倾斜。在蓄水调节前地下水渗流为由闸室墙后向闸室内渗流，由于闸室底板为透水底板，在蓄水调节期渗流变为从由闸室墙后填土侧渗流，在浮托力及渗透压力作用下，在蓄水调节期前后趾沉降均出现明显的回弹现象，且地基土沉降再此阶段已经基本趋于稳定，在此阶段月沉降值已经不足0.6 mm，在传统闸室地基沉降计算中应予以考虑。在此阶段闸室墙依然向填土侧倾斜，且倾斜量较蓄水调节前有所增大，但由图6的有限元结果及实测结果均可以看出前后趾沉降差值在此阶段已经趋于稳定，闸室墙倾斜在此阶段后期趋于不变。在蓄水调节阶段前后趾沉降差值有限元结果较实测结果偏大，但变化趋势基本一致。对比表3中的数据可以看出扶壁闸墙墙体倾斜主要控制因数为地基土的不均匀沉降所致的墙体倾斜，墙体挠度及扶壁底板变形所致的影响很小只占到10%左右，因此对于扶壁式闸墙预留倾斜量应当主要考虑前后趾沉降量的计算差值。

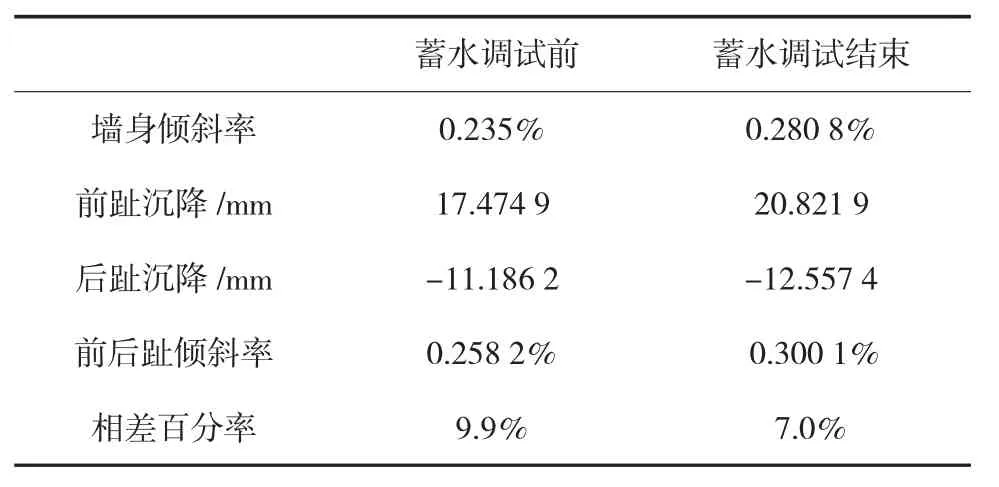
表3 墙身倾斜各因素分析

3.2 使用期灌泄水过程闸墙倾斜分析

本文模拟了在灌泄水过程中前、后趾土应力及水压力之和的变化及墙体倾斜的变化，有限元结果及实测资料均以灌水开始。图7为前、后趾土应力与水压力之和随灌泄水过程的变化趋势的有限元结果及实测结果，图8为闸墙墙顶水平向位移随灌泄水过程的变化。由图7可以看出在灌泄水过程中扶壁墙前趾及后趾的土应力及水压力之和均呈周期性变化，在灌水时土应力及水压力之和增大，在泄水时减小。由于作用在扶壁墙上的闸室面水压力及闸室内较大的水头压力靠近前趾，所以前趾的变化幅度大于后趾，有限元结果及实测结果的前趾变化幅度为6 kPa左右，后趾的变化幅度有限结果为2 kPa左右，实测结果为4 kPa左右，两者的变化一致。

由图8看出在灌泄水过程中扶壁墙墙顶的水平向位移也呈周期性变化，在灌水时向填土侧的水平位移增大，在泄水时向填土侧的水平位移减小，由于水头差较小前后趾水压力及土体应力变化较小，且由于灌泄水过程较短，墙顶水平向位移变化值很小，这与实测的结果相对应，在实际测量时灌泄水过程中墙顶的水平向位移变化幅度不超过1 mm。

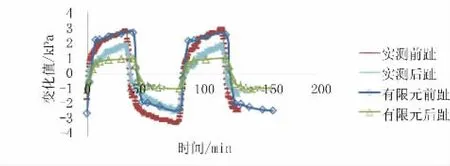
图7 水压力与土应力之和变化结果

图8 灌泄水过程中闸室墙顶水平位移有限元结果

4 结语

（1）扶壁式闸室在蓄水调节期间前后趾均有明显的回弹，且地基土的沉降在此期间已经基本稳定，在工程设计中应予以考虑。

（2）扶壁式闸室墙的变形主要控制因素为由于前后趾不均匀沉降导致的倾斜，墙体变形的影响较小，只占10%左右。因此对于对闸墙倾斜预测及预留倾斜量的确定，其主要依据前、后趾沉降差值。

（3）在闸室墙浇筑期间由于墙体重心靠近前趾，所以产生向闸室侧墙体倾斜，在回填土回填后墙体倾斜变为向填土侧倾斜，且随着地基土的不均匀沉降的增大而逐渐发展。在蓄水调节期趋于稳定。

（4）在灌泄水过程中，前、后趾水压力与土应力之和均呈周期性变化，灌水时前、后趾水压力与土应力之和增大，在泄水时间减小。同时扶壁墙墙体的水平位移也呈周期性变化。灌水时向填土侧的水平位移增大，泄水时减小。但水头差较小时，水平位移变化值很小。

参考文献：

[1]Burmistrov MA,Kotenkov YK.Field investigations of the static behavior of a navigation lock chamber[J].Hydrotechnical Construction,1967(3).

[2]JTJ307-2001，船闸水工建筑物设计规范[S].

[3]尹宗泽.土工原理[M].北京:中国水利水电出版社，2007.

[4]陈璐，刘永强.自重折扣法在坞式底板设计中的应用探讨[J].水利水电科技进展，1999，19（6）:41-43.

[5]JT S257-2008，水运工程质量检验标准[S].

[6]Roscoe K H,Schofield M A,Thurairajah A.Yield of Clays in States Wetter than Critical[J].Geotechinique,1963,13（3）:211-240.

[7]Burland J B.The Yielding and Dilation of Clay [J].Geotechinique,1965，15（2）:211-214.

[8]冯大江.应用Bi ot固结理论的船闸闸首结构非线性有限元分析[D].江苏南京:河海大学.2005.

[9]范庆来，栾茂田,杨庆.修正剑桥模型的隐式积分算法在A B A Q U S中的数值实施[J].岩土力学，2008，29（1）:269-273.

[10]费康，张建伟.Abaqus在岩土工程中的应用[M].北京:中国水利水电出版社，2010.

[11]姚甫昌，谢红建，何世秀.对修正剑桥模型的认识及试验模拟[J].湖北工学院学报,2004，19（1）:13-16.